星载大型天线反射器桁架展开动力学建模仿真

董富祥 周志成 曲广吉

（中国空间技术研究院，北京 100094）

1 引言

星载大型桁架式网状抛物面天线是满足移动通信、对地遥感和深空探测等空间应用的关键设备。这种天线尺寸大、质量小，常规的地面测试难以完全揭示其在轨展开动力学特性，因此，准确、可靠的展开过程多体系统动力学仿真，对于优化天线结构和机构设计、制定展开过程控制规律及预测天线在轨展开动力学性态，均具有重要意义，它是星载大型天线结构和机构设计、分析及验证不可或缺的工具［1-2］。

国内外针对大型周边桁架式网状抛物面天线展开动力学问题开展了大量研究。这些方法可以分为三类：节点笛卡尔坐标方法［3］、独立广义坐标方法［4］和利用商业软件的仿真方法［5］。以节点笛卡尔坐标为系统广义坐标，赵孟良、关富玲［3］采用广义逆矩阵方法研究了周边桁架式天线展开动力学过程，分析了桁架黏性阻尼和绳索滑轮摩擦作用对天线反射器展开动力学的影响。不过，节点笛卡尔坐标方法虽然便于描述桁架各部件平移运动，但由于缺乏描述铰链转角的广义坐标，因而难以建立旋转铰位置处摩擦力矩模型。李团结、张琰、李涛［4］以展开角为独立广义坐标，采用拉格朗日方法建立了周边桁架天线展开过程动力学方程，研究了重力、阻尼对天线展开动力学的影响。该方法导出的动力学方程不含约束，因此不必考虑动力学积分过程中约束方程违约问题。然而，反射器斜杆转角与展开角之间为复杂三角函数关系，导致斜杆动能对广义坐标速度的偏导数难以求解。李洲洋、陈国定、王三民等［5］基于ADAMS软件对星载大型可展开天线的展开过程进行了数值仿真。当前商业软件虽能较有效地处理运动过程中系统构型奇异问题，但难以解决静止状态下系统构型奇异问题。在小展开角情况下，反射器展开机构处于奇异构型附近，在从收拢状态到小角度展开过程中动力学方程左端系数矩阵接近奇异，导致数值仿真结果出现不稳定甚至发散。

本文以星载大型可展天线为对象，研究了反射器索网绷紧前星载大型天线反射器桁架在轨展开动力学过程，建立了反射器桁架卷簧驱动和同步齿轮传动机构力学模型，并针对初始时刻天线反射器切断铰约束方程雅克比矩阵奇异和小展开角情况下动力学方程左端系数矩阵数值性态差问题，提出了基于几何的替代约束解决方案。最后，结合算例对天线反射器展开动力学过程进行了数值仿真，并从物理角度解释了仿真结果的合理性。

2 星载大型天线系统组成及展开原理

星载大型天线系统主要由大小伸展臂、反射器和焦面馈源阵组成。图1为星载大型天线在轨工作状态示意图。

图1 星载大型天线在轨工作状态示意图Fig．1 Schematic view of large satellite antenna in orbit

初始时刻，天线在压紧机构的作用下处于锁定状态。展开时，捆束在反射器外围的火工切割器启爆，切断天线捆索，反射器桁架先后在卷簧和电动机作用下展开，反射器索网也由收拢状态逐渐拉开，最后在短时间内迅速张紧。图2 为反射器单个桁架单元展开过程。可以看出，天线反射器桁架单元由横杆AB、CD，竖杆AD、BC，斜杆DE、EB，旋转铰链B、D，滑移铰链E和同步齿轮A、C组成。初始时刻在铰链A、C处卷簧作用下，单元桁架展开，如图2（a）所示。天线展开到一定角度时，到达图2（b）所示位置，此时电动机启动，拖动伸缩套筒中拉索使天线桁架继续展开，直至天线单元完全展开到位并锁定，如图2（c）所示。限于篇幅，本文主要对卷簧驱动下天线反射器桁架展开过程进行多体动力学建模仿真。

图2 桁架单元展开过程示意图Fig．2 Deployment sequence of truss element

天线反射器桁架是一个含冗余约束的多体机构系统。假定天线反射器由30个平面桁架单元组成，它将包括150个运动部件、183个旋转铰、30个滑移铰和30对同步齿轮约束，其中3个旋转铰和1个同步齿轮约束为冗余约束。如果忽略天线制造装配误差引起的天线反射器不共面和形状不规则导致的系统自由度缩减，则反射器桁架系统的自由度为150×3-（183-3＋30）×2-（30-1）×1＝1。

3 星载大型天线多体动力学建模

3．1 基本假设

在卫星附件展开过程中，卫星相对于轨道坐标系仅存在扰动运动，因此可将当地轨道坐标系视为惯性参考基准［6-7］。对星载大型天线反射器桁架展开过程多体系统动力学建模作如下假设。

（1）反射器桁架展开过程中杆件结构振动可忽略不计，桁架各部件均作刚体假设。反射器各杆由轻质、高抗振碳纤维复合材料制成，刚度较大，展开过程中结构振动较小。

（2）反射器桁架各部件尺寸足够精确，制造及装配误差引起的单元各部件不共面和形状不规则可以忽略。

（3）暂不考虑铰链配合间隙和同步齿轮啮合间隙对反射器桁架展开过程的影响。

（4）暂不计及天线在轨展开过程中松弛状态索网对反射器桁架展开动力学的影响。在轨微重力环境下索网绝大部分时间内处于松弛状态，松弛状态索网对反射器桁架展开动力学的影响来自于索网运动状态改变引起的惯性效应，由于索网质量相对很小，因此反射器桁架在轨展开过程中松弛状态索网对天线反射器桁架展开动力学的影响可以忽略。

3．2 天线反射器展开过程多体系统动力学建模

根据天线反射器展开机构工作原理，其驱动装置主要包括卷簧和拉索驱动机构，传动机构则主要由旋转铰、滑移铰和同步齿轮组成。下面将分别建立天线反射器驱动和传动机构力学模型。

1）卷簧建模

图3为邻接物体间卷簧力元示意图，图中物体Bj为物体Bi内接物体，P与Q为重合的旋转铰铰点。

图3 卷簧作用示意图Fig．3 Diagram of coil spring

作用在内接物体Bj上的力矩Mj用于计算系统广义外力。

式中：Aj为内接物体Bj方向余弦矩阵；CQ为卷簧安装方向余弦矩阵；p为卷簧安装特征矢量列阵；K为卷簧刚度；qi为旋转铰相对坐标；θ0为卷簧初始压缩角。

根据作用力与反作用力原理，作用在外接物体Bi上的力矩为

2）同步齿轮

反射器桁架三支杆铰链位置装有同步齿轮，以保证天线展开过程中各桁架单元的同步性。图4为天线反射器展开过程中同步齿轮作用示意图，图中v表示齿轮啮合 位 置 速度，B（i-1）×5＋2和B（i-1）×5＋3分别为B（i-1）×5＋3和B（i-1）×5＋6的内接物体，其中i＝1，2，…，30。根据齿轮啮合原理，两齿轮在啮合位置切向速度大小相等，方向相反。

式中：ω1和ω2为同步齿轮1、2相对于框架（即物体B（i-1）×5＋3）的角速度；r为齿轮的节圆半径。

由于同步齿轮1为物体B（i-1）×5＋2的一部分，且旋转铰H（i-1）×5＋3为物体B（i-1）×5＋2的外接铰，这样

同步齿轮2为物体B（i-1）×5＋6的一部分，且旋转铰H（i-1）×5＋6为物体B（i-1）×5＋6的内接铰，因此

根据式（3）～（5），得到

图4 同步齿轮作用示意图Fig．4 Diagram of synchronization gear

假设反射器桁架由30个桁架单元组成，则系统的同步齿轮约束方程为

由于30个反射器桁架单元最终组成一个大闭环机构，且每个平行四边形桁架单元对角相等，因此物体B（30-1）×5＋2与物体B（30-1）×5＋3之间的同步齿轮约束和物体B（30-1）×5＋3与物体B1之间的同步齿轮约束彼此冗余。消除冗余约束后，反射器桁架的同步齿轮约束方程由29个同步齿轮约束组成，即

根据式（8），可以获得系统同步齿轮约束方程组的雅克比矩阵和加速度约束方程组的右端项为

3）反射器闭环桁架单元切断铰约束方程

天线反射器每个桁架单元均由2个闭环组成，选择物体B（i-1）×5＋1（i＝1，2，…，30）与B（i-1）×5＋3和物体B（i-1）×5＋3与B（i-1）×5＋5之 间 的 旋 转 铰 作 为 切 断铰CT1和CT2，如图5（a）所示。将以上铰链切断后，单个闭环桁架单元的拓扑构型如图5（b）所示。

图5 单个桁架单元切断铰示意图Fig．5 Diagram of cut joints of a single truss bay

每个平面桁架单元的旋转铰约束2个方向相对移动，其相对移动约束方程［8］为

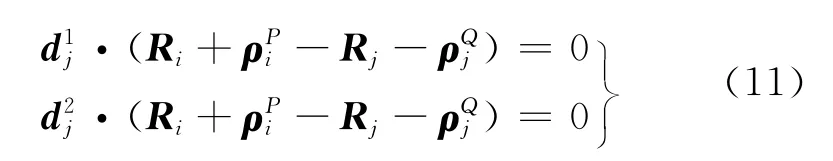
式中：和分别为物体Bj上特征矢量；Ri和Rj分别为物体Bi和Bj质心位置矢量；和分别为物体Bi和Bj上铰点矢量。

对式（11）求二阶偏导数，整理后可以得到反射器桁架切断铰约束方程［8］为

式中：Φi为第i个切断铰约束方程的雅克比矩阵；q为系统广义坐标列向量；γi为第i个切断铰加速度约束方程右端项。

假设系统存在m个反射器桁架单元，则反射器桁架系统的切断铰约束方程组的雅克比矩阵和加速度约束方程组的右端项为

4）基于相对坐标的星载天线反射器多体系统动力学方程

星载大型天线反射器桁架是由多个闭环桁架单元和同步齿轮约束副组成的非树状多体系统。考虑式（9）～（10）和式（13）～（14），其多体系统动力学方程可写为

式中：Z为星载大型天线多体系统广义质量阵；z为包含系统广义外力在内的动力学方程右项；λcj为与切断铰约束有关的拉格朗日乘子；λgc为与同步齿轮约束有关的拉格朗日乘子；fey为非理想约束力阵。

5）奇异构型求解技术

初始时刻天线反射器各部件均收拢于竖直位置，此时物体B（i-1）×5＋1与B（i-1）×5＋3（i＝1，2，3，…，30）之间切断铰约束导出的雅克比矩阵奇异，且小展开角范围内动力学方程（式（15））左端系数矩阵条件数过大，导致动力学方程无法求解或者数值仿真结果发散。

对于奇异构型引起的雅克比矩阵亏秩问题，已经提出了很多解决方案，如罚函数法［9-10］、约束稳定和违约修正结合的方法［11］，这些方法虽能处理运动过程中系统构型奇异问题，但难以求解静止状态下系统构型奇异问题。从数值上看，初始位置约束雅可比矩阵奇异意味着系统出现额外的冗余约束，如果采用基于约束相关性分析的选独立坐标方法直接去除这些“冗余约束”，则相当于额外增加了系统的自由度。为了获得正确结果，需要计算机从删除冗余约束导致的多种运动可能性中将真实运动自动选择出来，然而初始时刻反射器处于静止状态，难以提供算法自动选择所需要的足够信息，下面将根据反射器桁架设计原理解决这一问题。为了保证天线反射器能够正常展开，反射器每个桁架单元均需要设计成平行四边形机构。根据平行线基本定理，可得

根据式（16），可以形成替代约束雅可比矩阵为

替代约束矩阵的右端项为

将式（17）、（18）代入到式（15）中，替换原来出现奇异的雅可比矩阵，得到

式中：Φcj，f为切断铰非奇异雅克比矩阵；λcj，f为与Φcj，f有关的拉格朗日乘子；γcj，f为切断铰中非奇异切断铰加速度约束方程右端项；λcj，r为与替代约束雅克比矩阵有关的拉格朗日乘子。

4 算例

以30个桁架单元组成的天线反射器为例，研究星载大型天线在卷簧驱动下反射器桁架展开多体系统动力学过程，初始时刻天线反射器处于收拢状态，如图6所示。星体、大小臂及反射器各物体质量、惯量信息和几何数据均由CAD模型提供。假设各同步齿轮铰链位置处弹簧刚度0．8Nm／rad，初始时刻卷簧扭转角为π／2，各类铰链位置处静摩擦系数为0．4，动摩擦系数为0．3，旋转铰链位置处摩擦力半径为0．003m，滑移铰初始重叠量为0．093m。

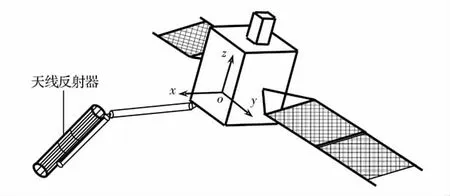
图6 星载大型天线展开初始状态示意图Fig．6 Diagram of deployment status of large antenna

天线反射器展开过程中，计及铰链摩擦情况下系统总机械能-时间历程曲线如图7所示。可以看出，计及铰链摩擦阻力的情况下，系统总机械能呈下降趋势，但到天线反射器完全展开时仍存在较大剩余动能，由于未考虑接近展开到位时索网绷紧产生的阻力效应，这部分剩余动能将给反射器桁架带来一定的冲击。

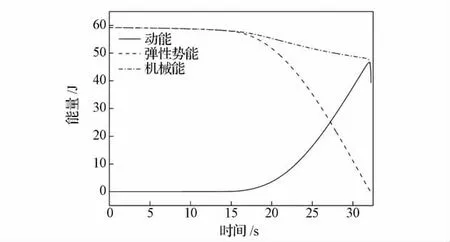
图7 计及铰链摩擦情况下系统机械能时间历程Fig．7 Mechanical energy with considering hinge’s friction during reflector deployment

图8为计及铰链摩擦情况下天线反射器在轨展开过程中整星系统质心相对于星本体质心时间历程曲线。可以看出，反射器展开过程中整星系统质心在星体坐标系x轴和z轴方向偏移量随着反射器展开而不断增加，到反射器完全展开到位时偏移量达到最大。

图8 在轨展开过程中系统质心相对星本体质心时间历程Fig．8 Time history of system mass center relative to satellite body during deployment in orbit

图9为反射器展开过程中星本体角速度时间历程曲线。由于反射器沿垂直于俯仰轴平面展开，因此展开过程中星体角速度在俯仰轴方向变化最大。当反射器接近展开到位时，星体绕俯仰轴方向角速度仍较大，这是由于反射器接近到位时在y轴方向上仍存在较大速度，根据动量矩守恒原理，星体在该方向上具有相应的角速度。以上分析说明控制反射器在轨展开速度既有助于降低反射器展开到位时刻冲击，同时也有利于减小展开过程星体角速度，仿真结果还表明本文提出的方法能够避免初始时刻天线反射器桁架展开机构约束方程雅克比矩阵奇异问题，完成其展开全过程动力学仿真。

图9 反射器展开过程中星体角速度时间历程Fig．9 Angular velocity history of satellite body during reflector’s deployment

5 结束语

本文采用基于相对坐标的递推方法，研究了星载大型天线反射器展开动力学过程，建立了卷簧驱动机构模型和同步齿轮传动机构模型，给出了含切断铰约束的星载大型天线反射器桁架在轨展开多体系统动力学方程。针对初始时刻天线反射器切断铰约束方程雅克比矩阵奇异和小展开角情况下动力学方程左端系数矩阵数值性态差问题，根据天线反射器桁架机构设计原理，提出了基于几何的切断铰约束替代解决方案。最后，结合算例研究了大型天线反射器在轨展开动力学过程，并从物理角度解释了仿真结果的合理性。

（References）

［1］Mitsugi J，Ando K，Senbokuya Y，et al．Deployment analysis of large space antenna deployment analysis of large space antenna using flexible multibody dynamics simulation［J］．Acta Astronautica，2000，47（1）：19-26

［2］Meguro A，Harada S，Watanabe M．Key technologies for high-accuracy large mesh antenna reflectors［J］．Acta Astronautica，2003，53：899-908

［3］赵孟良，关富玲．考虑摩擦的周边桁架式可展开天线动力学分析［J］．空间科学学报，2006，26（3）：220-226

Zhao Mengliang，Guan Fuling．Deployment dynamic analysis of circular truss deployable antenna with friction［J］．China Journal of Space Science，2006，26（3）：220-226（in Chinese）

［4］李团结，张琰，李涛．周边桁架可展天线展开过程动力学分析及控制［J］．航空学报，2009，30（3）：444-449

Li Tuanjie，Zhang Yan，Li Tao．Deployment dynamic analysis and control of hoop truss deployable antenna［J］．Acta Aeronautica Et Astronautica Sinica，2009，30（3），444-449（in Chinese）

［5］李洲洋，陈国定，王三民，等．大型可展开天线的展开过程仿真［J］．机械设计与制造，2006（7）：67-69

Li Zhouyang，Chen Guoding，Wang Sanmin，et al．Simulation of deploy process of hoop truss deployable satellite antenna［J］．Machinery Design ＆ Manufacture，2006（7）：67-69（in Chinese）

［6］章仁为．卫星轨道姿态动力学与控制［M］．北京：北京航空航天大学出版社，1998

Zhang Renwei．Dynamics and control of satellite orbit and attitude［M］．Beijing：Beijing University of Aeronautics and Astronautics Press，1998（in Chinese）

［7］曲广吉．航天器动力学工程［M］．北京：中国科学技术出版社，2000

Qu Guangji．Spacecraft dynamics engineering［M］．Beijing：China Science and Technology Press，2000（in Chinese）

［8］洪嘉振．计算多体系统动力学［M］．北京：高等教育出版社，1999

Hong Jiazhen．Computational dynamics of multibody system［M］．Beijing：High Education Press，1999（in Chinese）

［9］Bayo E，Avello A．Singularity-free augmented Lagrangian algorithms for constrained multibody dynamics［J］．Nonlinear Dynamics，1994，5：209-231

［10］Bayo E，Ledesma R．Augmented lagrangian and mass-orthogonal projection methods for constrained multibody dynamics［J］．Nonlinear Dynamics，1996，9：113-130

［11］齐朝晖，许永生，方慧青．多体系统中的冗余约束［J］．力学学报，2011，43（2）：390-399

Qi Zhaohui，Xu Yongsheng，Fang Huiqing．Study on redundant constraints in multibody systems［J］．Chinese Journal of Theoretical and Applied Mechanics，2011，43（2）：390-399（in Chinese）