探究立体几何课程学习的有效方法
2012-12-28高长玉
高长玉
(淮南市第二中学,安徽 淮南232001)
探究立体几何课程学习的有效方法
高长玉
(淮南市第二中学,安徽 淮南232001)
立体几何是培养学生逐步形成空间想象能力的主要载体,在实践的基础上总结了立体几何学习的九种方法。
立体几何;学习方法
一、引言
立体几何是培养学生逐步形成空间想象能力的主要载体。很多人在学习立体几何时感到困难,主要是因为没有掌握有效的学习方法。“工欲善其事,必先利其器”。笔者在教学实践基础上提出九个方法,以供商槯。
二、学习立体几何的有效方法
1.画
对于一个空间几何体,想象其空间图形并画出来,对学习立体几何是非常有益的,要让所画(或所看到)的“立体”图形,真正地在脑海中“立”起来。否则对于类似下面简单的问题也会得到错误的答案。
如图 1, α∩β=AB,AC⊂α,BD⊂β, 若∠1=∠2,则AC∥BD。这种让人啼笑皆非的答案,正是缺乏空间观念导致的。
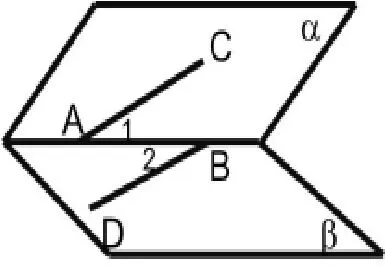
图1
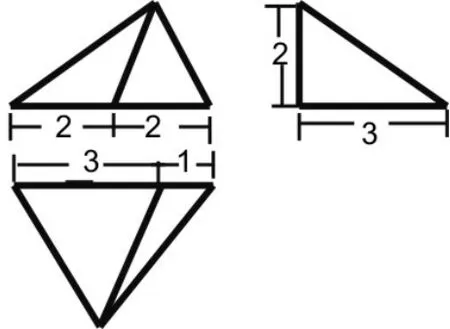
图2
2.拉
根据“长对正,高平齐,宽相等”,不难由几何体画出相应的三视图,但往往难以由三视图想象出相应的几何体。如下面的问题:
某几何体的三视图如图2(尺寸长度单位为m),则该几何体的体积为__m3。
事实上只要以俯视图为突破口,抓住关键的点或线拉一拉,几乎所有三视图的问题甚至勿需画图即可解决。如本题中把俯视图中A点沿着垂直于纸面方面拉一拉,拉起来的高度为2;并且俯视图是底边长为4,高度为3的三角形,求其体积便是一件很自然的事情。
3.记
概念、公理、定理自然要记,但一些重要的中间结论同样也要记。只是不能死记,要在理解的基础上去记。有时,利用这些结论可以很快地解决一些运算起来很繁琐的题目,尤其是在求解选择题或填空题时。对于解答题虽然不能直接运用这些结论,但我们可以把这些结论先证出来再加以运用。如数一个几何体有多少对异面直线,往往数一个几何体有多少个四面体(因为四面体模型中有三对异面直线)就可以了。
4.辩
一个命题由平面过渡到空间,正确的要能证明,错误的要举出反例。即便都是空间的命题,有些比较相近的内容也容易混消,因此学习时一定要辩一辩,彻底地弄明白,不留死角,不留盲点。
如“平行于同一条直线的两条直线平行”与“垂直于同一条直线的两条直线垂直”;又如在证明一个几何命题时,什么时候用判定定理,什么时候用性质定理,都要用心辨别。一般而言,由未知,想判定;由已知,想性质。
5.嵌
有没有把一个非标准的几何体嵌入到标准的几何体(如:长方体)中的意识,涉及到我们有没有转化与化归的数学思想。如:
如图3,正四面体ABCD的顶点A、B、C分别在两两垂直的三条射线上,则在下列命题中,错误的是()
A.O-ABC是正三棱锥
B.OB∥面ACD
C.AD与OB成450
D.二面角D-OB-A为450
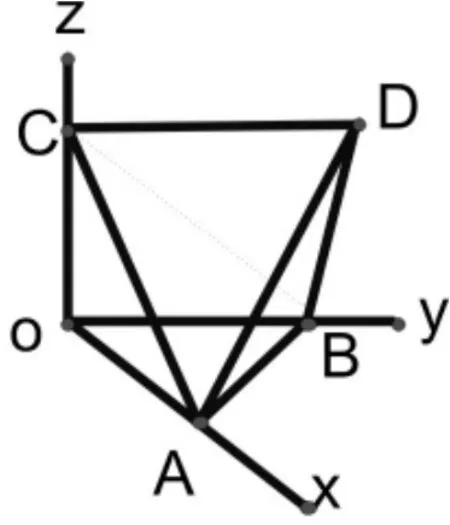
图3
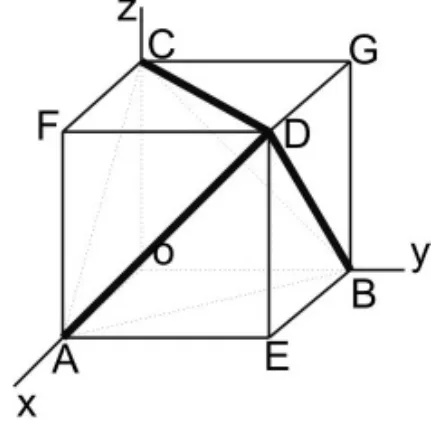
图4
本题若直接计算,将费时费力。如果将所给的四面体嵌入到正方体OAEB-CFDG(如图4)中,很快就会选出正确答案(B)。
6.猜
猜想能激发学生的求知欲,猜想正确时会感受到猜想的乐趣,享受到成功的喜悦,学生会以更大的热情投入新知的探求中。在教学过程中通过适时、适度的引导,启发学生猜想,可以将新知纳入到整个知识体系之中。
7.变
有些学生时常满足一知半解,做题时照葫芦画瓢,不能领会实质,不能掌握解决该类题的通性通法,这与近几年高考的要求是相左的。因此必须从题海中解脱出来,要学一题,得一法,会一类。如人教版数学课本《必修2》第二章复习参考题B组第2题:
如图5,在正方体ABCD-A1B1C1D1中,求证:
(1)B1D⊥平面 A1C1B;
(2)与平面 的交点H是△A1C1B的重心(三角形三条中线的交点)。
本题由两问组成,显然是为了控制难度,尤其是第一问证出以后,很容易得到H是△A1C1B垂心的结论,而△A1C1B又是正三角形,为第二问的解决铺平了道路。但本题是课本复习参考题中的最后一题,作为本章的压轴题,如果至此结束,对学生思维能力的提高以及空间想象能力的形成都是一种遗憾。我们不妨将其变一变:
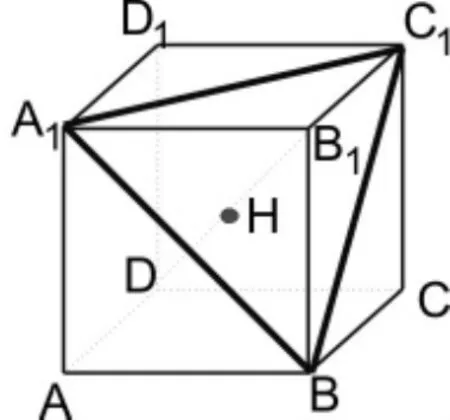
图5
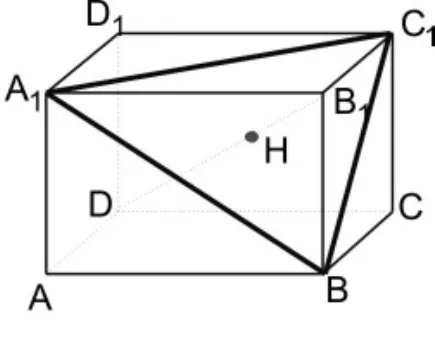
图6
如图6,已知长方体ABCD-A1B1C1D1,请问:
(1)B1D⊥平面 A1C1B 吗?
(2)B1D与平面A1C1B的交点H是△A1C1B的重心吗?
以上两问,如果正确,给出你的证明;如果不正确,说明理由。
事实上,第(1)问是一个假命题,是想让同学们知道如何说明一条直线与一个平面不垂直;而第(2)问正是基于通性通法而考虑的,怎样正确作出B1D与平面A1C1B的交点H是解决本题的关键。我们可以这样思考:点H一定要变成同一平面内两条直线的交点,那么就要在含B1D的面中寻求另一条直线。我们自然想到平面BDD1B1,如图7,不难发现平面BDD1B1与平面A1C1B有两个公共点B、O1(为了便于学生观察,平面BDD1B1用红色,平面A1C1B用蓝色,姑且称B、O1为双色点),显然B、O1是这两个平面的交线,而易知点H是这两个平面的公共点。因此,H⊂BO1且BO1∩B1D;接下来,BO1是△A1C1B的中线且BH=2HO1都是很显然的。就这样,从已知到未知,又从未知到已知,寻求正反两方面知识衔接点之间的一个固有的或确定的数学关系,使问题得以顺利解决。
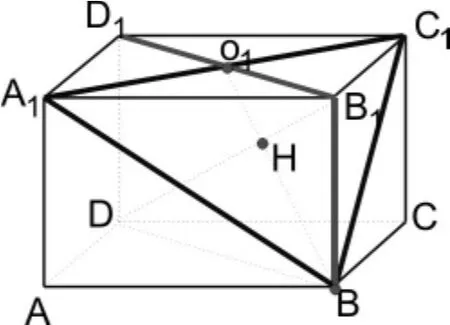
图7
8.换
波利亚指出:“解题过程就是不断变更题目的过程,对一个数学问题,改变它的形式,换一种叙述方式,变换它的结构,直到发现有价值的东西,这是解题的一个重要原则。”例如下面一道求直线与平面所成角的问题:
如图8,正方体ABCD-A1B1C1D1中,求BB1与平面BC1D所成角的正切值。
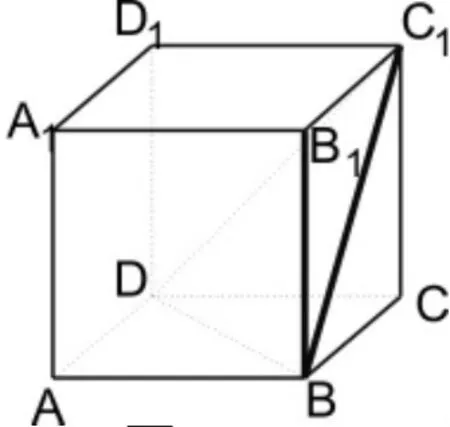
图8
思路一:可以利用VB1-BDC1=VD-BB1C1求点B1到平面BDC1的距离,把问题换成求直线与平面所成角的正弦值;
思路二:也可以把“求BB1与平面BC1D所成角的正切值”换成“求CC1与平面BC1D所成角的正切值”,这样一来三棱锥C-BDC1正是长方体一角模型,由直角顶点向底面作高,同学们非常熟悉;
思路三:注意A1C到与平面BC1D垂直的事实,本题也可换成求异面直线BB1与A1C所成角的问题。
可以看出,通过不断转换命题的形式,把它转化为一类已经解决或是较容易解决的问题,可使问题由繁变简,由难变易,由暗变明。
9.算
立体几何计算题,单纯的计算往往无济于事,必须辅之必要的空间想象及必要的逻辑推理。
如图9,设ABCD-A1B1C1D1是一个棱长为2的正方形,点 M 是 AB的中点,过 M、B1、C、D1四点作一个球,则该球的半径为 。
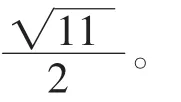
如果能建立空间直角坐标系如图10,设球心O 的坐标为(x,y,z),因为|OM|=|OB1|=|OC|=|OD1|,利用空间两点之间的距离公式不难解决;但如果能注意到球心在 AC1上,故可设球心O的坐标为(t,t,t),则只需要利用|OM|=|OB1|即可解决。
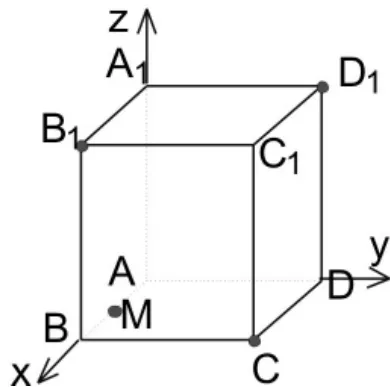
图9
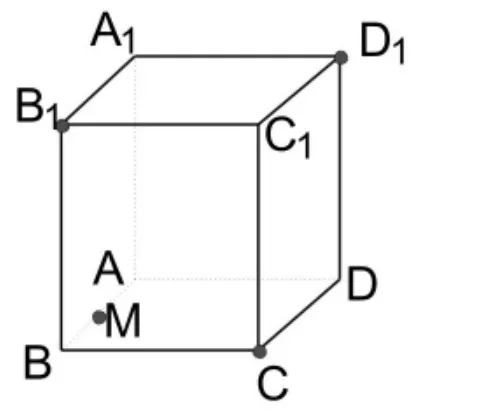
图10
三、结语
以上笔者提出了9个方法学习立体几何这些方法已经在长期的教学实践中得到检验。当然,学好立体几何还要注意与其它知识的有机联系。不过九九归一,学之道在于悟。只善于思考,善于总结,落实一个“悟”字,才能真正领会和掌握这些学习方法的精髓。
[1]郑强,邱忠华.走进高中数学教学现场[M].北京:首都师范大学出版社,2008
G633.63
A
1009-9530(2012)03-0140-03
2012-03-17
高长玉(1962-),男,淮南市第二中学特级教师。
