基于GIS和DEM的水系三维分形计盒维数的计算

范 林 峰，胡 瑞 林，张 小 艳，王 珊 珊，袁 延 西

基于GIS和DEM的水系三维分形计盒维数的计算

范 林 峰1，胡 瑞 林1，张 小 艳1，王 珊 珊1，袁 延 西2

（1.中国科学院工程地质力学重点实验室，中国科学院地质与地球物理研究所，北京 100029;2.西安科技大学地质与环境学院，陕西 西安 710054）

实现具有三维立体特征的河网水系分形维数的准确计算，是目前分形地貌学面临的主要问题之一。该文依据三维分形计盒维数的基本原理，提出基于DEM和ArcGIS的水系三维分形计盒维数的计算方法，并以湖北省恩施市境内水系为例，验证了方法的可靠性，说明三维计盒维数比二维计盒维数更能反映水系的空间分布特征和内部结构。

三维计盒维数;分形;DEM;GIS

分形理论逐渐成为处理复杂性系统的有力工具，在地貌学领域尤其是在水系研究中应用广泛［1－10］。在众多分形维数中，计盒维数由于简单实用，得到了广泛应用。何隆华［1］提出根据水系的计盒维数划分流域地貌侵蚀发育阶段的方法;邹谨敞等［2］利用计盒维数法分析甘肃中部及邻区水系的分形特征及其与滑坡分布的关系;盘小东等［3］计算了浑江断裂带水系的计盒维数，并分析了水系分形特征与构造活动性的关系;马宗伟等［4］分析了长江中下游河流的分形特性，并在此基础上分析了不同水系特征下洪水的特点;孙祝友等［5］应用GIS技术提取了莱州湾东岸河流信息，并运用计盒维数法对莱州湾东岸的黄水河和王河水系进行分形分析;韩杰等［6］在滑坡泥石流灾害区划中应用水系分形维数的空间变化表征水系空间形态特征的差异，从而反映云南省滑坡泥石流灾害发生的程度。目前对水系分形维数的计算大多是在二维平面上进行的，然而，天然沟谷中的水系具有三维立体特征，要得到关于水系空间形态和内部结构真正客观、科学的研究结论，必须对三维空间中的水系分形特征进行深入探讨。本文根据分形理论，利用ArcGIS软件的空间分析功能，计算水系的三维分形计盒维数。

1 利用DEM生成水系

河网水系分布图是计算水系三维分形维数的必备资料之一，可以由数字高程模型（DEM）自动提取。目前最常用的提取方法是坡面流模拟法，依据水总是沿斜坡坡度最大方向流动的原理，首先确定DEM中每个栅格单元的水流方向，据此计算每个栅格单元的上游给水区，再选择合适的集流阈值确定河网。由于该方法依据水文学汇流概念判别水流路径，被认为是一种较好的方法;但仍存在一定问题，即DEM中不能存在局部凹陷和平坦的栅格单元，否则会使水流无法确定。因此，在提取河网水系之前，需要对DEM进行预处理，包括洼地的确定、填充和平地的抬升，再利用经过洼地填充处理的DEM源数据生成水系。上述操作过程可在ArcGIS软件中实现，由于篇幅所限，在此不再赘述。

2 三维计盒维数的计算模型

目前研究中使用的计盒维数一般是二维计盒维数。计算时，首先用边长为r的正方形网格覆盖二维分形图形，得到与图形相交的非空网格数Nr，逐步改变网格的边长r，得到一系列Nr值。二维计盒维数可用下式表示：

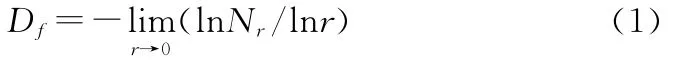
式中：Df为研究对象的计盒维数。

本文的研究对象是三维空间中的水系，不能用二维正方形网格覆盖，而应采用三维小立方体对空间水系进行覆盖，计算被水系占据的小立方体的数目（图1）;不断变换小立方体的边长，得到一系列被水系占据的小立方体数目，进而求得水系的三维计盒维数。这里，核心的问题是如何计算被水系占据的小立方体的数目。

要解决这个问题，可首先在XOY二维平面上用不同边长的正方形网格覆盖二维水系分布图，确定非空网格;再由水系高程，确定XOY平面内非空网格对应的水系在Z轴上占据的小立方体数目（图2）。

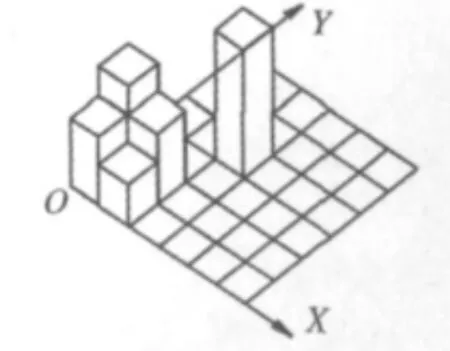
图1 立方体覆盖示意Fig.1 Schematic diagram of cube covering

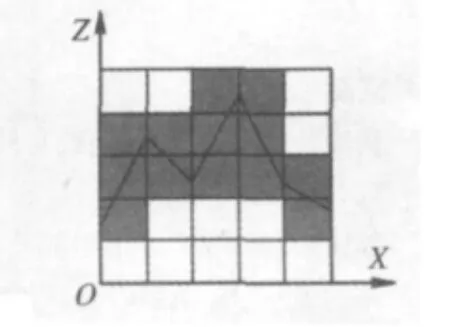
图2 立方体个数计算Fig.2 Counting of covering cubes

XOY平面内每个非空网格对应的水系在Z轴上占据的小立方体数目可由下式计算：

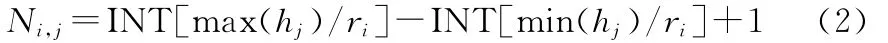
式中：Ni，j为用边长ri的正方形网格覆盖时，第j个非空网格对应的水系在Z轴上占据的立方体数目;ri为小正方形网格（即小立方体）的边长;max（hj）、min（hj）分别为第j个非空网格对应的水系的最大、最小高程;INT为向下取整运算。

以边长为ri的小立方体对水系进行覆盖时，被水系占据的小立方体的总数Ni为：

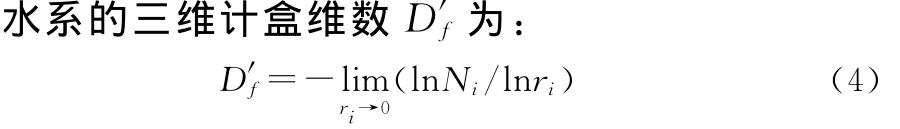
3 三维计盒维数的计算过程

基于上述计算模型，可以根据研究区的DEM和水系分布图，利用ArcGIS的空间分析功能，计算水系的三维计盒维数。计算步骤如下：1）在XOY平面内生成边长为ri的Fishnet网格，并将其由线状要素转化为面状要素，生成面域网格;2）将面域网格与二维水系分布图求交，确定二维平面上被水系占据的非空网格;3）利用ArcGIS的Zonal Statistics功能，求出每个非空网格内水系的最大高程max（hj）和最小高程 min（hj）;4）由式（2）和式（3）计算用边长为ri的小立方体对三维水系进行覆盖时，被水系占据的小立方体数目Ni;5）改变Fishnet网格边长ri，重复上述步骤，得到一系列Ni值;6）将Ni和ri值绘入双对数坐标系，由式（4）求得研究区水系的三维计盒维数。

4 计算实例

本文以湖北省恩施市境内的清江水系（图3、图4）为例，按照上述模型计算出水系的二维和三维分形计盒维数（图5、表1）分别为1.18和1.26。

图3 恩施二维水系分布Fig.3 2D river system in Enshi

图4 恩施三维水系分布 Fig.4 3D river system in Enshi

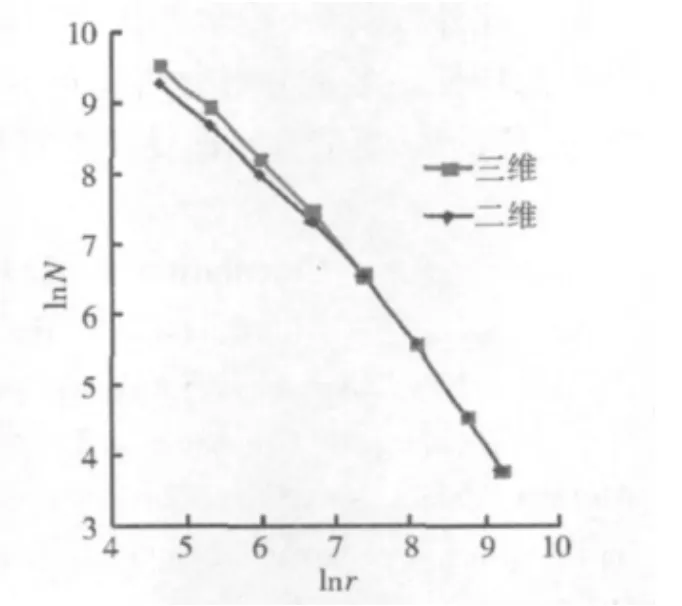
图5 水系二维和三维计盒维数计算结果 Fig.5 Ln-ln plot of Ni and ri for 3D and 2D fractal dimension

表1 水系二维和三维计盒维数计算Table 1 Calculation of 3D and 2D fractal dimension of river system

5 结果分析与讨论

（1）欧式几何中，直线的维数是1，三维实体的维数是3。三维空间中的水系可以看做是空间曲线段的集合，其计盒维数应该在1～3之间。本文的计算结果与上述分析一致，且与文献［11］的结果相近，因此可以认为本文提出的方法是可行的。

（2）从表1和图5可以看出，三维空间内lnNi值大于二维平面的lnNi值，且二者的差值随着ri的增加有逐渐减小的趋势。当ri≥3 200 m时，二者的差值为0，即覆盖水系所需的小立方体数目与正方形网格数目相等。这是由于当非空正方形网格内三维水系的最大高程和最小高程接近到一定程度时，在Z轴上仅需要1个立方体即可将此网格对应的三维水系覆盖（式（2））。由此可以看出，对于地形起伏较小的地区，水系的三维计盒维数与二维计盒维数将十分接近，三维水系分形维数更适用于地形起伏较大的地区。

（3）利用本文方法计算水系的三维分形维数受原始数据的精度影响较大。由于本文采用的DEM分辨率是90 m，因此，本文将小立方体的最小尺寸设置为100 m。当DEM的数据精度提高时，应该采用更小尺寸的立方体对研究区的水系进行覆盖，从而获得更为精确可靠的计算结果。

（4）对水系的分形研究大多采用计盒维数法，主要是因为该方法简单方便。但是，该方法仅考虑被水系占据的正方形网格和小立方体数目，而没有考虑每个正方形网格和小立方体中水系的条数或长度，由此计算出的分形维数不能完全反映空间水系的分形结构特征。信息维由于考虑了每个正方形网格和小立方体中水系的条数，因而能弥补这方面的不足。此外，还有一些学者认为空间水系具有多重分形的特征。多重分形分析比单分形分析（如计盒维数、信息维）更能真实地反映空间水系的复杂性和本质特征，所获得的标度指数和多重分维可以从整体上反映出水系的多重分形结构特征，而奇异指数和分维谱函数则能反映出水系多重分形的局部特征。因此，需进一步研究空间三维水系的多重分形特征。

［1］何隆华.水系的分形维数及其含义［J］.地理科学，1996，12（2）：124－128.

［2］邹谨敞，邵顺妹.甘肃中部及邻区水系分形研究结果与滑坡分布的关系［J］.地震研究，1994，17（4）：383－388.

［3］盘晓东，康力.浑江断裂带及水系的分形特征和构造活动性研究［J］.东北地震研究，2002，18（1）：7－15.

［4］马宗伟，许有鹏，李嘉峻.河流形态的分维及与洪水关系的探

讨——以长江中下游为例［J］.水科学进展，2005，16（4）：530－534.［5］孙祝友，杜国云，李德一，等.基于GIS技术的莱州湾东岸河流

分形研究［J］.测绘科学，2007，32（3）：120－121.

［6］韩杰，陆桂华，李海涛.水系分维在滑坡泥石流灾害区划中的应用［J］.自然灾害学报，2009，18（4）：63－71.

［7］朱俊江，詹文欢，唐诚，等.水系的分形特征与红河断裂带活动性关系初探［J］.华南地震，2002，22（1）：1－7.

［8］连建发，刘传正，高尚嵘.三峡库区沟谷水系的分形几何特征研究［J］.勘察科学技术，2006（6）：25－28.

［9］马宗伟，许有鹏，钟善锦.水系分形特征对流域径流特性的影响——以赣江中上游流域为例［J］.长江流域资源与环境，2009，18（2）：163－169.

［10］杜尚海，苏小四，朱琳.松花江流域地表水系分形维及其影响因素分析［J］.水文，2009，29（5）：30－35.

［11］朱晓华.地理空间信息的分形与分维［M］.北京：测绘出版社，

2007.77－84.

Calculation of 3D Box Dimension of River System Based on GIS and DEM

FAN Lin－feng1，HU Rui－lin1，ZHANG Xiao－yan1，WANG Shan－shan1，YUAN Yan－xi2
（1.KeyLaboratoryofEngineeringGeomechanics，InstituteofGeologyandGeophysics，CAS，Beijing100029;2.CollegeofGeologyandEnvironment，Xi′anUniversityofScienceandTechnology，Xi′an710054，China）

Calculation of the fractal dimension of 3D river system is one of the major problems in fractal geomorphology.Based on the principle of box counting method，a method to calculate the 3D fractal dimension of river system based on ArcGIS and DEM is proposed.Enshi was used as an example to verify the reliability of this method.The results indicate that 3D box dimension can reflect more information about the spatial distribution and inner structure of river system than 2D box dimension.

3D box dimension;fractal theory;DEM;GIS

P 64;P208

A

1672－0504（2012）06－0028－03

2011－12- 11;

2012－03－29

国家科技支撑计划课题“重大滑坡、泥石流灾害综合风险评价技术”（2008BAK50B04－3）;中国科学院知识创新工程项目“地震地质灾害的内外动力耦合作用机制”（KZCX2－YW－Q03－2）;湖北省交通运输厅科技项目“宜巴高速公路岩溶隐患辨识与风险防范研究”

范林峰（1988－），男，硕士研究生，主要从事地质灾害风险评价方面的研究。E－mail：fanlinfeng1988＠163.com