关于“线性代数”课程教学改革的几点思考

赵俊芳，陈旭东，廉海荣

中国地质大学(北京) 数理学院,北京 100083

关于“线性代数”课程教学改革的几点思考

赵俊芳，陈旭东，廉海荣

中国地质大学(北京) 数理学院,北京 100083

“线性代数”是高等院校理工类和经济管理类等专业的一门重要的公共基础课程,也是抽象难学的一门课程。本文从“线性代数”教学实践中发现的问题出发,剖析其存在的原因,总结了在课程建设中的一些教学体会。

线性代数;教学改革;基础课程

“线性代数”是高等院校理工类和经济管理类等专业的一门重要的公共基础课程,也是一门应用广泛的工具学科。学好该门具有较强抽象性与逻辑性的课程,对于培养学生的抽象思维能力、空间想象能力、逻辑推理能力,以及建立数学模型解决实际问题的能力等都具有十分重要的意义。

当前,随着计算机应用技术的深入发展和各类型数学软件的开发应用,用代数的方法解决实际问题已经渗透到如计算机图形学、密码学、机器人学等众多学科,线性代数的地位作用显得越来越突出,对于高等院校学生来说,学好线性代数知识显得更加紧迫和必要。但是教学实践中发现,很多学生感到“线性代数”课程的内容相对抽象,知识量过大,缺乏研究趣味性和应用联系性,在课时相对较少的情况下不易充分接受,难以透彻理解,有时达不到较好的教学效果。如何使学生更好地掌握课程主要内容,培养学生熟练的运算能力、严密的逻辑思维能力以及灵活的应用能力,是教师教学活动中函待思考解决的主要问题。笔者根据自己的教学实践,有以下几点教学体会。

一、提高学生的学习兴趣和积极性是打开教学局面的首要问题

“兴趣”是最好的导师,只有把学生的学习兴趣和积极性真正激发出来,才能顺利打开线性代数的教学局面。

1.及时纠正思想偏差

任课老师准备一堂“附加课”,给予学生良好的数学学科教育。首先要讲到该学科对大学教育后续课程的重要支撑性,现在没有体会到数学的作用,是因为还没到一定的层次和阶段,增强学生全力投入到学习的信心。突出强调该门学科在理论物理、理论化学、工程技术、国民经济、生物技术、航天航海等领域中的广泛应用性,教育学生要想在本专业领域有所建树,必须学好“线性代数”等重要的数学课程。以此使学生把主要心思和精力集中到线性代数学习中来。

2.按时对内容进行精练介绍

教师应在每次教学展开前,对“线性代数”课程的重点内容和主要脉络进行归纳梳理,对该节课程的基本内容、基本方法及教学目的有一个明确的认识和理解。同时,联系学生所学专业方向,从学生的具体实际出发,向学生介绍线性代数知识的概况、精要和未来发展趋势,将学生个人目标与线性代数学习的目标有机结合,使学生对教学内容产生期待,保持长久的学习动力。

3.适时开展实例引导

教师可以结合自己的情况或所研究的实际课题,给学生简单介绍讲授的内容在哪些领域得到应用。比如,当引入矩阵时,可以飞机航线问题为例进行讲解(图1）。

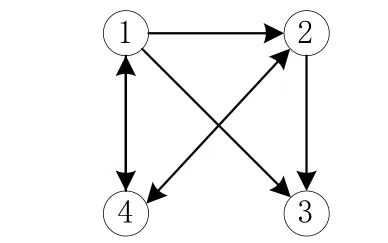
图1 城市之间航空航线图

图1描述了四个城市之间的航空航线图,其中1,2,3,4表示四个城市,带箭头线段表示两个城市之间的航线。设行号表示起点城市,列号为到达城市,则该航空航线图可用矩阵表示,其中,矩阵的第i行描述从城市i出发,可以到达各个城市的情况,若能到达第j个城市,记A(i,j)=1,

在讲矩阵乘法时,仍可用这个例子,让学生发现A2=A*A表示一个人连续坐两次航班可以到达的城市,矩阵A3=A*A*A表示连续坐三次航班可以到达的城市。这样一来,学生就可以看到线性代数在现实生活中的应用,从而可以激发其进一步学习的兴趣。

二、培养学生掌握有效的学习方法是实现教学目标的根本保证

线性代数的核心是线性空间与线性变换,研究的对象是线性方程组,研究的内容是线性方程组解的存在性与解的结构等问题,研究的工具包括矩阵、行列式等。围绕线性方程组这些核心问题,线性代数还研究了矩阵及其运算、向量、向量组、线性变换等。知识点很多,学生初学时总感到很庞杂,很零碎。因此,培养学生掌握有效的学习方法特别重要。

1.知识点联系法

要教学生善于总结前后知识点的联系。例如,矩阵的秩和向量组的秩的关系,矩阵的秩在教材上是用它的子式的行列式来定义的,向量组的秩是用向量组的极大无关组来定义的,从定义上似乎没有看到二者的联系,但事实上如果将矩阵的一行看成一个向量,矩阵可以看做一个行向量组。同理,如果将矩阵的一列看成一个向量,则矩阵可以看做一个列向量组,矩阵的秩=行向量组的秩=列向量组的秩,由此可以看到二者之间的关系。要特别注意不同概念的区别与联系,比如,行列式和矩阵的异同,其区别是行列式是对n行n列数表进行的一种运算,其结果是一个数,而矩阵是一个m行n列的数表,其联系是:当m=n时就可以去求一个矩阵的行列式。“等价”、“相似”、“合同”三者关系,“等价”是指两个同型矩阵如果它们具有相同的秩,则它们是等价的,而“相似”与“合同”都是特殊的等价关系,但它们只是对方阵而言。类似于这样的近似的概念在线性代数中还有很多,如果教师不加以引导强调,学生很容易混淆,张冠李戴,久而久之,学生就会越弄越糟。所以,在教学过程中,教师应鼓励学生在听课前先预习,带着问题去听课。

课堂上,教师要及时带领学生总结、概括、归纳,这样可以收到事半功倍的效果。另外,教师在引入时应将抽象概念具体化,将复杂概念简单化:如,引入逆矩阵的概念时,可以由数中“倒数”的概念引出,在数域中,如果一个数a≠0,ab=1,则称b为a的倒数,记为或b=a-1,我们知道矩阵中单位阵E从某种意义上可以看做数域中的1,那么如果对于一个方阵A,存在一个方阵B使得AB=E,B就可以称为方阵A的逆,类似的,我们记B=A-1,这样,学生就很容易接受逆矩阵的概念了,并且,由“零”在有限意义下不存在倒数这一结论学生很容易猜想出方阵A可逆的充要条件为“|A|≠0”。

2.多概念比较法

线性代数中有大量的概念,这些概念是导出定理和运算法则的逻辑基础,教师要强调概念的重要性,要求学生首先掌握概念。数学是一门相当严谨的科学,作为高等院校重要基础数学课之一的线性代数毫无疑问也是如此,线性代数中的每一个概念,少一字则不清楚,多一字则累赘,所以,解释概念时要逐字逐句地解释。比如,方阵的特征值和特征向量的概念,设A是n阶方阵,如果数λ和n维非零列向量x使关系式Ax=λx成立,那么这样的数λ称为矩阵A的特征值,非零向量x称为A的对应特征值λ的特征向量,教材中黑体部分均为需强调部分,特别需要学生注意的是特征向量必须是非零向量,并且不能单单说是某个矩阵的特征向量,而要说清楚是对应于哪个特征值的特征向量。这些细节在学生们一接触这个概念时就讲清楚,就会使学生有一个良好的基础,更有利于后续知识的学习。

3.启发诱导法

在讲课过程中,教师可以设问,引起学生思考,激发对未知探索的欲望。教师可以启发学生自己概括抽象出一个数学概念,比如极大无关组的概念,给一个向量组α=(1 0 0)T,β=(0 1 0)T,γ=(1 1 0)T,很显然 γ=α+β,α=γ-β,β=γ-α,也就是说,这个向量组中的所有向量只需用两个向量就可以完全表出,如果我们把这两个向量称为该向量组的极大无关组的话,那么“极大无关组”的定义应该怎么给出呢,这个时候学生自然会去思考,这样他们的记忆就会比较深刻。当然,教师也要适时地给予正确的引导,如过早的引导,等于是索然无味的简单灌输,但如果过迟,容易使已有知识呈现零乱状态。因此,教师把握好时间节点,适时总结出定义。

三、采取灵活多样的教学手段是增强教学实效的重要途径

科学合理、形式丰富的教学手段可以起到对学习的促进作用,反之,会打击学生的积极性,影响教学质量的提高。

1.布置适当的课堂练习

在课堂上,教师是课堂教学的主导者,学生是教学的主体,整个课堂不能一味地是老师讲,学生听,而应该教师调动学生,让学生也动起来,脑动,手也动。学习中,学生能积极参与、努力思考,学习成绩也会明显提高。讲完一个知识点后,教师可以出一个简单的练习,让学生在5分钟内计算出来,这样一方面可以使学生更好地掌握课堂知识,另一方面可以调动学生的学习积极性,在整节课学生都处于活跃状态。

2.与Matlab等数学软件的使用有机结合

即利用计算机做数学实验,数学实验的目的是提高学生学习线性代数的积极性,提高学生对数学的应用意识并培养学生应用所学的数学知识和计算机技术去认识和解决实际问题的能力。不同于传统的数学学习方式,数学实验是强调以学生动手为主的数学学习方式。在数学实验中,由于计算机的引入和数学软件包的应用,为数学的思想与方法注入了更多、更广泛的内容,使学生摆脱了繁重乏味的数学演算和数值计算,促进了数学同其他学科之间的结合,从而使学生有时间去做更多的创造性工作。

3.融入数学建模的思想

数学建模过程不仅培养学生综合运用各个方面知识解决实际问题的能力,而且培养学生的语言表达、科技写作、创新精神、团队合作等多方面的能力。在“线性代数”教学改革中适当融入建模思想,有利于学生整体综合素质的提高,适应素质教育的要求,让学生终生受益。例如:在行列式定义的引入时,如果仅仅告诉学生这是求解方程组的需要,由于缺乏应用背景,学生会感到非常空洞且难于理解,为此可以模拟法国数学家柯西求解空间多面体模型体积的过程,从平行四边形面积和空间六面体体积出发,得到2阶和3阶行列式的基本公式,从而引发学生对高阶行列式公式推导的兴趣。在矩阵概念的引入时,可以从诺贝尔经济学奖获得者美国经济学家和数学家里昂惕夫的投入产出模型出发,建立简单的投入产出模型,引导学生构建低维直接消耗矩阵,有了实际应用背景,学生学习的目的性会更加明确。

[1] 褚宝增,王祖朝.线性代数[M].北京大学出版社.

[2] 王军霞,张世中,苗秀花.工科代数课程教学改革的探索与实践[J].中国地质教育,2010,(3):49-53.

[3] 秦静.线性代数教学改革点滴[J].工科数学,2000,(4):95-97.

[4] 平怡.Matlab在大学数学教学中的应用研究[J].湖北广播电视大学学报,2008,(4):135-136.

[5] 陈怀琛.线性代数要与科学计算结成好伙伴[J].大学数学,2010,(26):28-34.

Reform on the Course of Linear Algebra

ZHAO Jun-fang, CHENG Xu-dong, LIAN Hai-rong
China University of Geosciences, Beijing 100083,China

Linear Algebra is an important fundamental course in science and economics colleges, which is also an abstract and difficult course to learn.In this paper, we listed the problems we has encountered in teaching practice, and then analyzed these problems. We summarized some personal thoughts and specific countermeasures during the course construction.

linear algebra; teaching reforms; fundamental course

G642

A

1006-9372 (2012）02-0100-03

2012-02-16;

2012-04-12。

赵俊芳,女,讲师,主要从事微分方程边值问题的教学和研究工作。