伪黎曼流形上的Simons型不等式

杨慧章，穆 凤

（红河学院数学学院，云南 蒙自 6661100）

伪黎曼流形上的Simons型不等式

杨慧章，穆 凤

（红河学院数学学院，云南 蒙自 6661100）

是n维黎曼流形到n+p维伪黎曼流形的等距浸入．通过计算Ricci张量长度平方的拉普拉斯算子，得到了伪黎曼流形上的一个Simons型积分不等式．

伪黎曼流形；Ricci张量；拉普拉斯算子

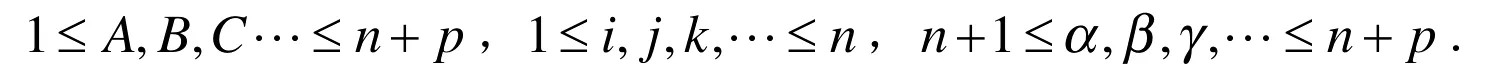
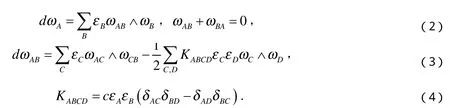
限制在M上有

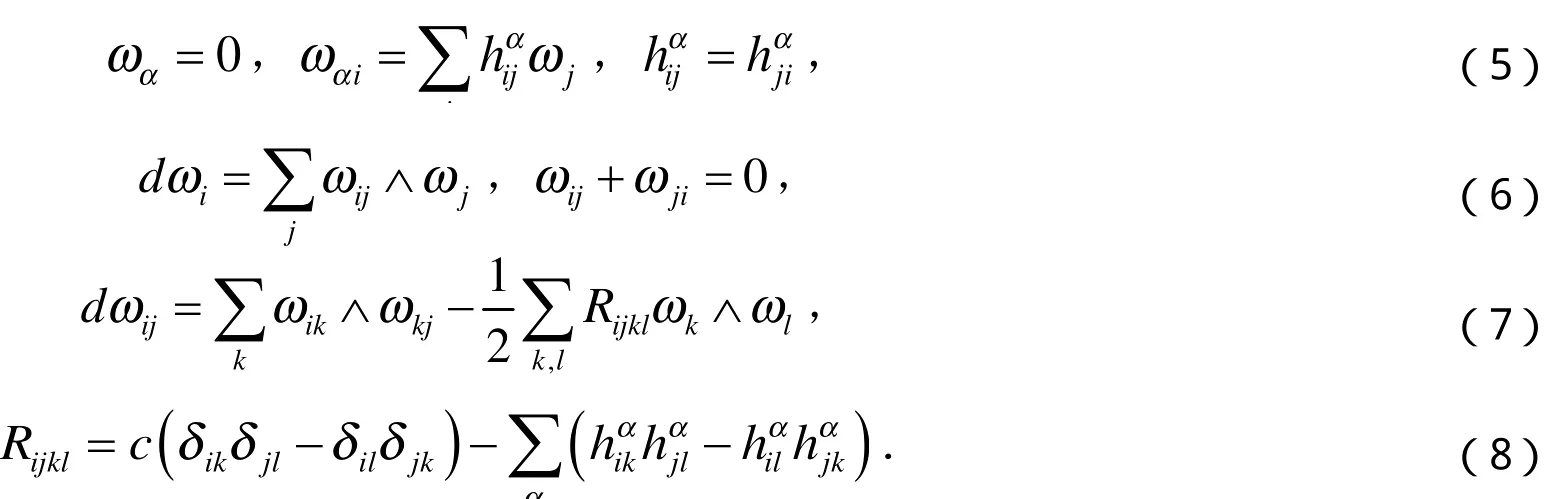
还有

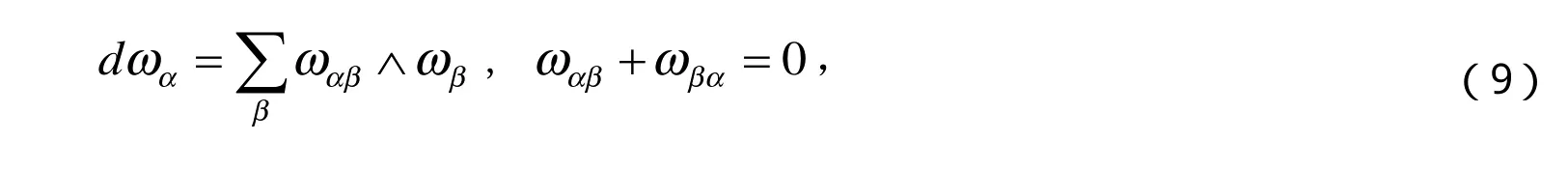
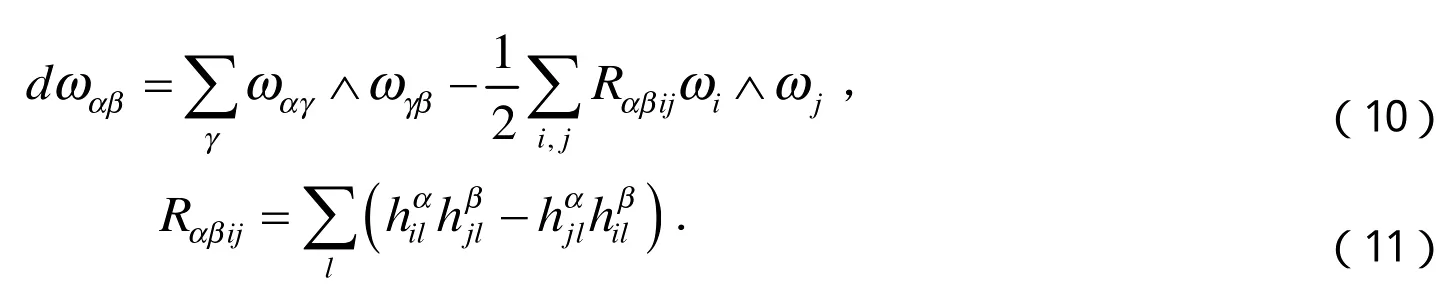
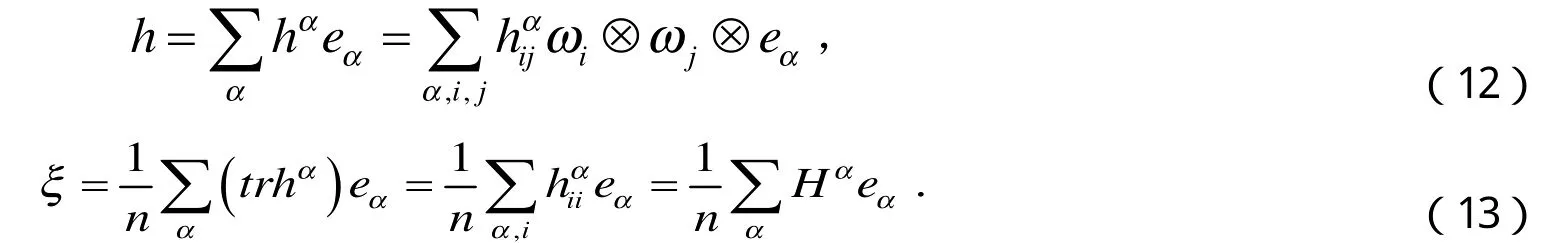
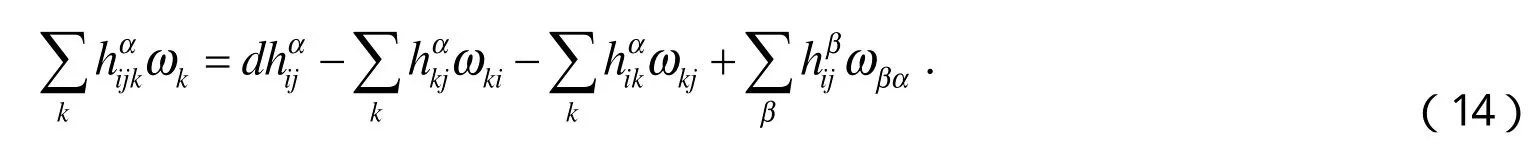
Codazzi方程为

Ricci恒等式为

由（8）式得，M的Ricci曲率为

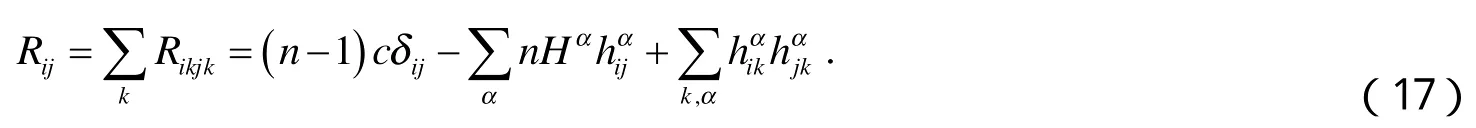
定义Ricci张量的共变导数如下：

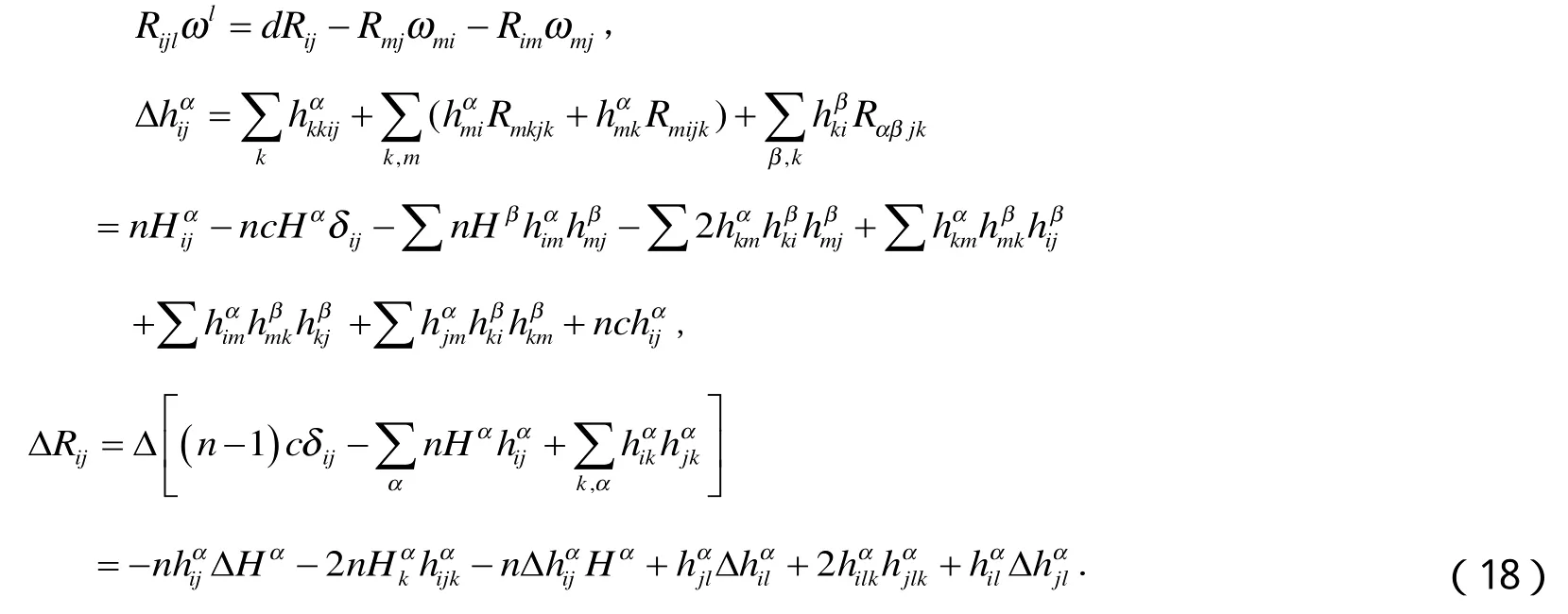
由于Mn为中的极大类空子流形，由（17）、（18）式及M的极大性得

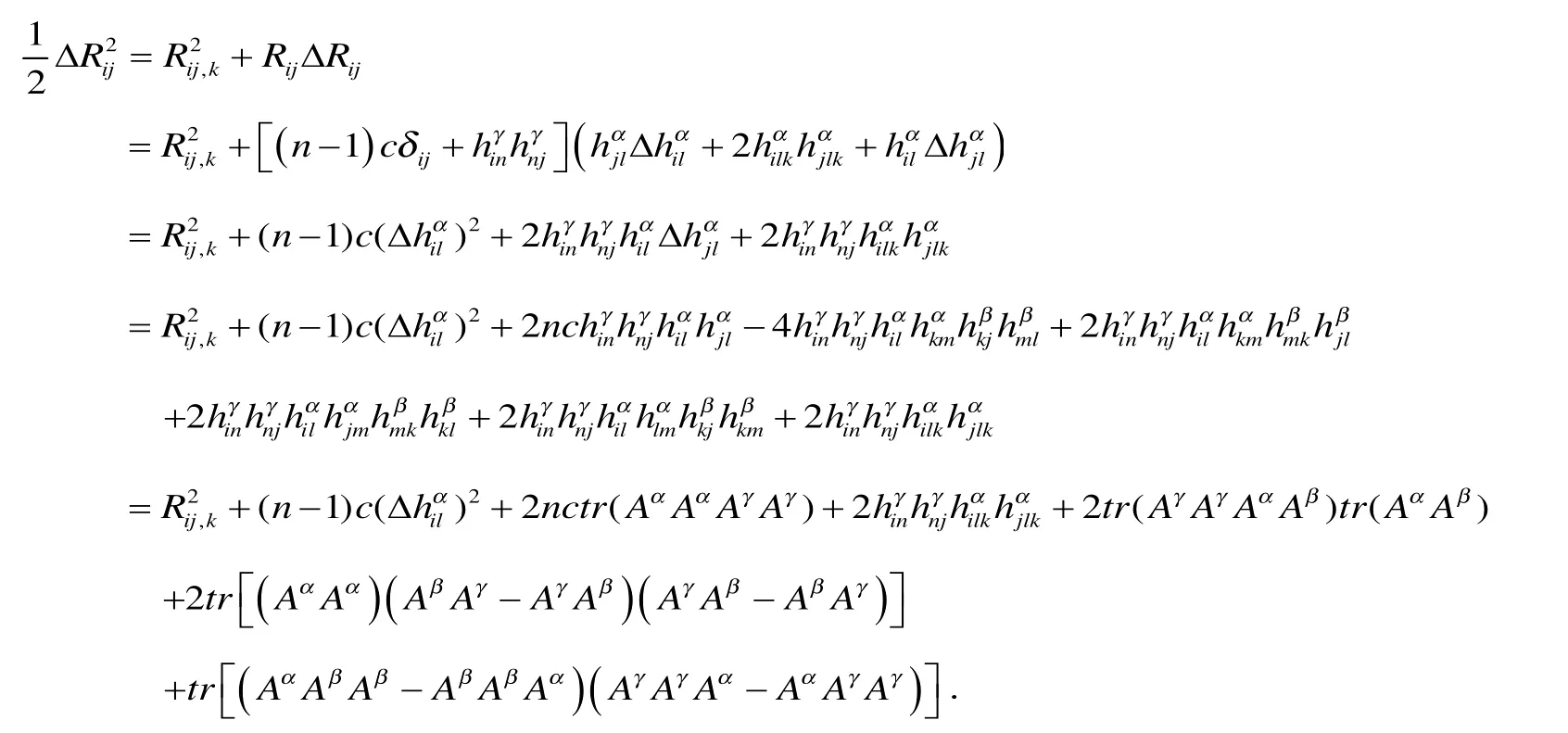
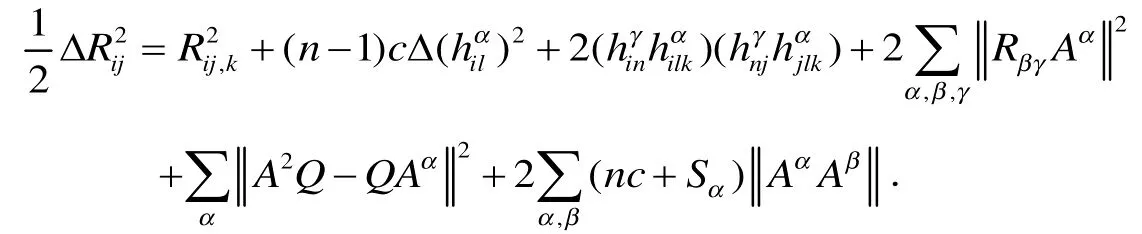
由于M为紧致的极大类空子流形，对上式两边积分有

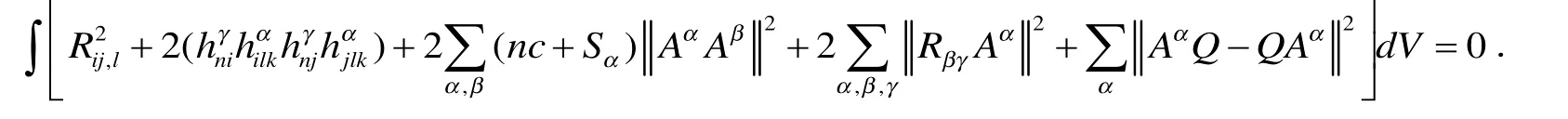
由此易得下面的定理：

定理 若M为紧致的极大类空子流形，则有

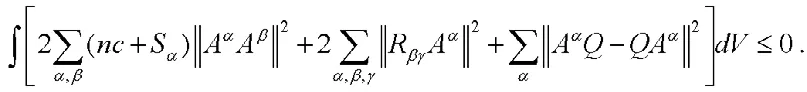
文中通过计算Ricci张量Laplaian算子，从内蕴量的角度给出了伪黎曼流形中紧致极大类空子流形的一个Simons型积分不等式．关于此不等式在伪黎曼流形中的应用，还需进一步的研究．

[1] Chern S.S., Do Carmo M, Kobayashi S.Minimal submanifolds of a sphere with second fundamental form of constant length[J].Functional Analysis and Related Field.Berlin, Springer-verlag.1970, 59-75.

[2] Xu Hongwei.On closed minimal submanifolds in p inched Riemannian manifolds[J].TransAmerMath Soc, 1995, 347 (5) :1743～1752.

[3] Takabashi T.Minimal immersions of Riemannian manifolds[J].Math.Soc.Japan,1960, 18:380-385.

[4] SONG Weidong , ZHANG Liang.An integral inequality of Simons’type[J] .Journal of Anhui Normal University:Natural Science Edition ,2003 ,26 (3) :205 - 208.

[5] 陈六新,郭震,李同柱.一个新的Simons 型不等式[J].西南师范大学学报,2003,28(4):533-535.

A Simons’ Type Inequality in Pseudo-Riemannian Manifold

YANG Hui-zhang,MU Feng
(Department of Mathematics, Honghe University, Mengzi 661100,China)

Letbe a n-dimensional Riemannian manifold isometrically immersed into (n+p)-dimensional pseudo-Riemannian manifold.By calculat ing the Laplacian of the square of the length of Ricci curvature, a new Simons’ integral inequality is obtained in the pseudo-Riemannian manifold.

pseudo-Riemannian manifold; Ricci curvature; Laplacian

O186.13

A

1008-9128（2012）02-0029-03

2011-10-19

红河学院科研基金（10XJY121）

杨慧章（1982—），女，昆明人，硕士，讲师.研究方向：微分几何．

[责任编辑 张灿邦]