一类带附加装置的特殊刚体的稳定性分析

梁建莉

（华侨大学 数学科学学院，福建 泉州 362021）

一类带附加装置的特殊刚体的稳定性分析

梁建莉

（华侨大学 数学科学学院，福建 泉州 362021）

研究一类带有附加装置的特殊刚体的稳定性，通过寻找合适的Poisson结构及Hamilton函数，将刚体的运动方程转化为广义Hamilton系统.运用能量Casimir函数法分析得知，这类刚体的运动在一定条件下是稳定的.

特殊刚体；稳定性；Poisson结构；Hamilton函数；能量Casimir函数法

1 预备知识

在研究几何空间中刚体的定点转动时，可用刚体相对于固定在质心上的直角坐标的3个角动量作为动态变量［1］，其相空间为P＝｛m＝（m1，m2，m3）｜mi为角动量.在这个相空间上，自由刚体的运动由Euler方程描述为

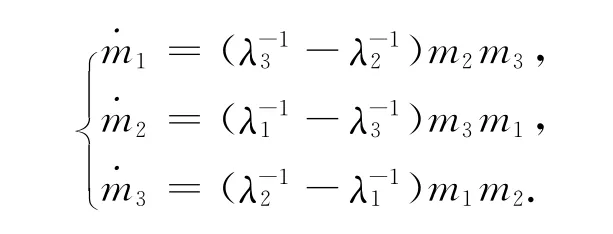
其中：λi是主惯性矩，λi＞0.

文献［2］应用能量Casimir函数法和谱分析法，证明在自由刚体运动中绕长轴和短轴的转动是稳定的，绕中轴的转动是不稳定的.对于带附加装置的特殊刚体，其运动方程为

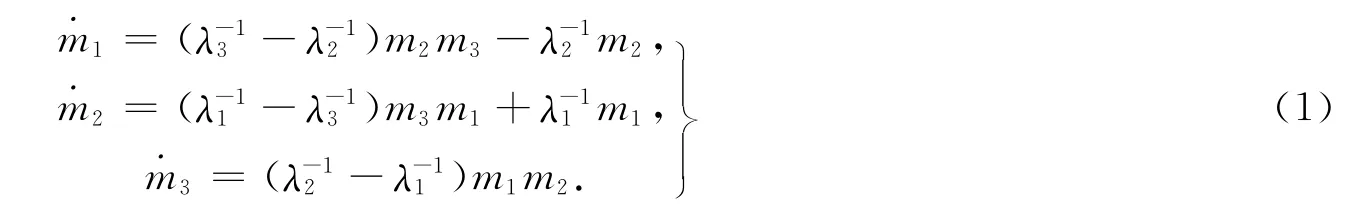
本文通过寻找合适的Poisson结构及Hamilton函数，运用能量Casimir函数法［2-3］得到如下定理.

定理1 a）若主惯性矩λ3＞max｛λ1，λ2｝，则当角动量为

时，带附加装置的刚体运动是稳定的；

b）若主惯性矩λ3＜min｛λ1，λ2｝时，则当角动量为

时，带附加装置的刚体运动是稳定的.

2 基本定义和引理

定义1［4］常微分方程

称为广义 Hamilton系统 .如果存在 Hamilton函数 H（x）及n阶反对称矩阵J（x）＝［Ji，j（x）］n×n，使得方程可以写成

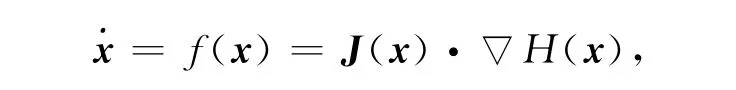
并且J（x）满足Jacobi恒等式

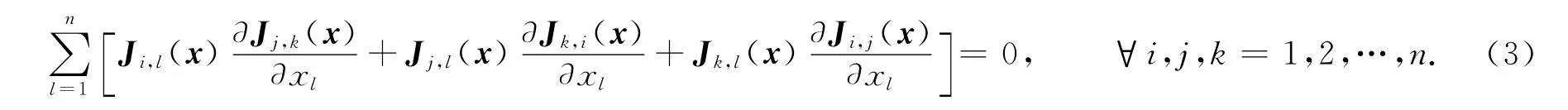
式（3）中：矩阵J（x）称为广义Hamilton系统的Poisson结构.

定义2［4］如果函数C（x）满足方程

则函数C（x）称为Poisson结构J（x）的Casimir函数.

通过直接计算可知，若C（x）是J（x）的一个Casimir函数，那么对于任意的一元可微函数Φ（z），复合函数Φ［C（x）］也是J（x）的Casimir函数.

定义3［4］微分方程（2）在奇点x0是形式稳定的，如果存在方程组（2）的一个满足下列条件的守恒量H（x）：

1）DH（x0）＝0；

2）D2H（x0）是正定或负定的.

其中：DH（x0）是 H（x）在x0点的梯度；D2H（x0）是 H（x）在x0点的 Hessian矩阵.

定义4［4］设x（t）是微分方程（2）的任一解.微分方程（2）的奇点x0称为是Liapunov稳定（或非线性稳定）的，如果对于任意ε＞0，存在δ＞0，当｜x（0）－x0｜＜δ时，对于一切t＞0，有｜x（t）－x0｜＜δ；如果还有x（t）＝x0，则称x0是渐近稳定的.

对于有限维系统来说，形式稳定与Liapunov稳定是等价的，而对于无穷维空间则不是如此.

引理1［2］Hamilton函数和Casimir函数都是广义Hamilton系统的守恒量.

引理2［2］Hamilton函数加上任何Casimir函数仍可作为原系统的Hamilton函数.

引理3［2］即Lagrange－Dirichlet引理 .设x0是 Hamilton系统

能量Casimir函数法是引理3的推广.

对于证明经典Hamilton系统的奇点稳定性问题，一个有效的办法就是利用引理3.即寻找系统的一个守恒量，使其在奇点处具有局部极大或极小值，在经典Hamilton力学中，这个守恒量通常取Hamilton函数.在广义Hamilton系统中，其Hamilton函数在奇点处不一定取到极大或极小值.

由引理2可知，Hamilton函数加上任何Casimir函数仍为原系统的Hamilton函数，因此要寻找守恒量C（x），用H（x）＋C（x）替代H（x）成为系统新的守恒量，使其在奇点处可以取到极大或极小值.

能量Casimir函数法有如下3个主要步骤：

1）构造适当的Poisson结构及Hamilton函数H（x），使系统成为广义Hamilton系统；

2）求Casimir函数C（x），对系统的奇点x0有D（H＋C）（x0）＝0；

3）验证D2（H＋C）（x0）＝0的定性.

3 定理的证明

3.1 Poisson结构及Hamilton函数

首先，取反对称矩阵为

由此可以验证J（m）满足Jacobi恒等式（3）.

其次，取哈密顿函数为

则刚体的运动方程（1）可以写为

即系统（1）是一个广义Hamilton系统，且J（m）为此系统的Poisson结构.

3.2 Casimir函数

设Casimir函数为C（m），由J（m）·▽C（m）＝0，得到偏微分方程组为

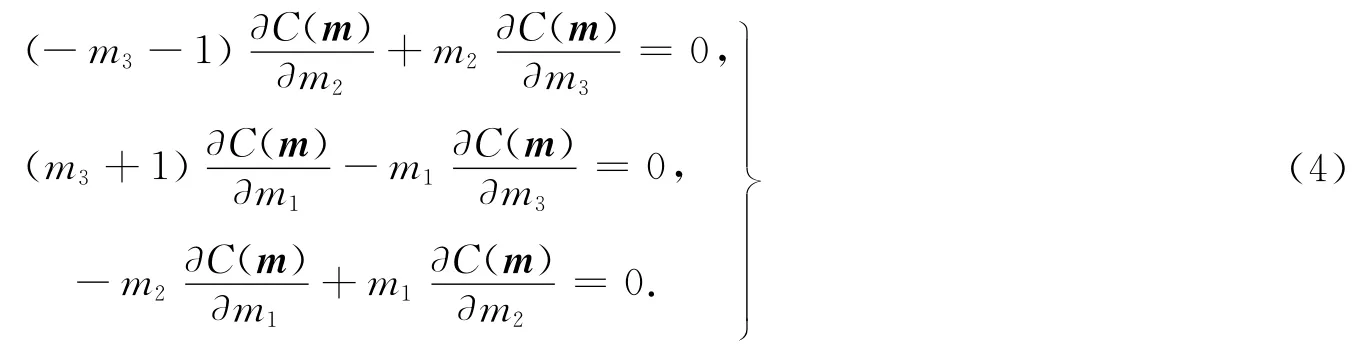
利用偏微分方程原理［5］，通过计算可知，m21＋m22＋（m3＋1）2为J（m）的Casimir函数，若Φ（z）为一个一元可微函数，则C（m）＝Φ（m21＋m22＋（m3＋1）2）也是J（m）的Casimir函数，所以系统（1）的另一个哈密顿函数为

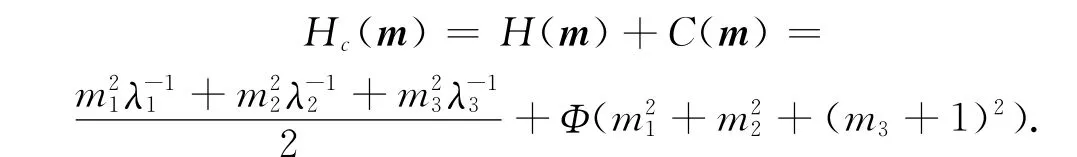
其梯度为

考虑系统的奇点m0＝（0，0，m3），即m3轴上的点均为系统的奇点.

令DHc（m0）＝0，则

即所选取的Casimir函数C（m）要满足式（5）.

3.3 验证D2 Hc（m0）的定性

令

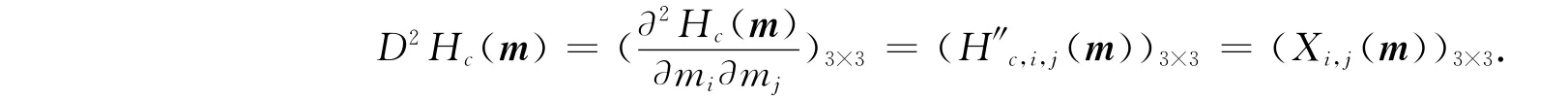
由此可得，在奇点m0处，Xi，j（m0）＝0，i≠j，所以得到矩阵为

若D2Hc（m0）正定，则其所有顺序主子式为正，从而Xi，i（m0）＞0（i＝1，2，3），即

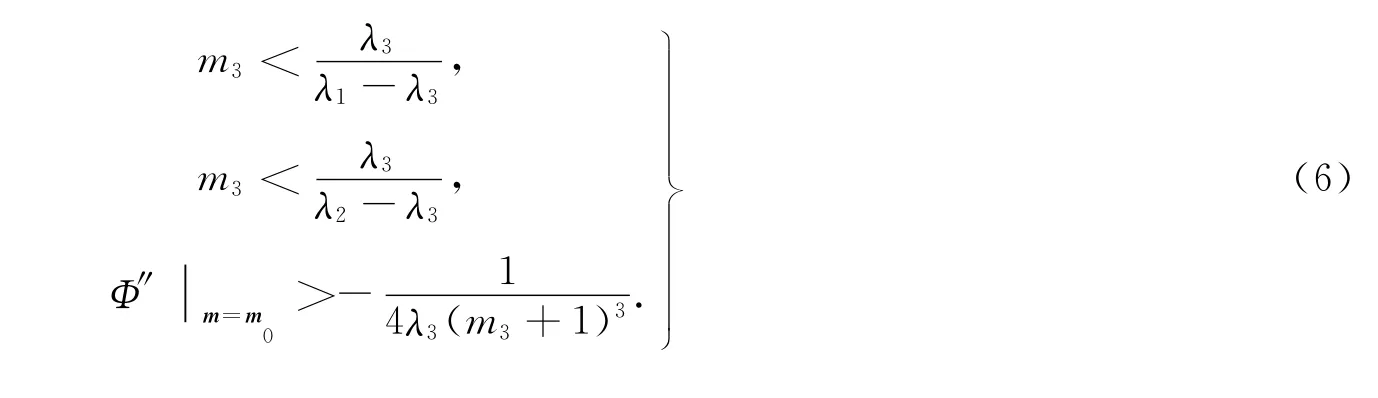
因此，只要取一元可微函数为

则Φ（z）满足式（5），（6）的第3式.

由式（6）的前两式可得，若主惯性矩λ3＞max｛λ1，λ2｝，则当角动量

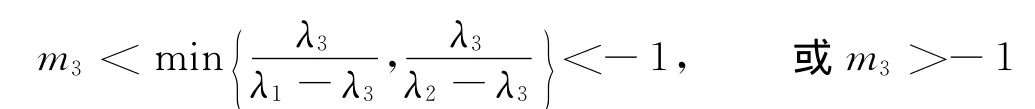
时，刚体的转动是稳定的.

同理，若D2Hc（m0）负定，则Xi，i（m0）＜0（i＝1，2，3）.此时，只要取一元可微函数为

通过计算可知，若主惯性矩λ3＜min｛λ1，λ2｝，当角动量为

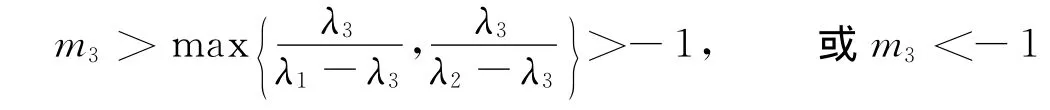
时，刚体的转动是稳定的.定理得证.

［1］李继彬，赵晓华，刘正荣.广义哈密顿系统理论及其应用［M］.北京：科学出版社，1999.

［2］高普云.非线性动力学：分叉、混沌与孤立子［M］.长沙：国防科技大学出版社，2005.

［3］王照林，匡金炉.利用能量Casimir方法研究充液对称刚体的非线性稳定性［J］.力学与实践，1993，15（2）：34－37.

［4］赵晓华，黄克累 .广义 Hamilton系统与高维微分动力系统的定性研究［J］.应用数学学报，1994，17（2）：182－191.

［5］管志诚，李俊杰.常微分方程与偏微分方程［M］.浙江：浙江大学出版社，2001.

Stability of a Special Rigid Body with Additional Devices

LIANG Jian－li
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

In this paper，we study the stability of a special kind of rigid body with additional devices.The rigid body′s motion equations is transform into a generalized Hamilton system by means of a suitabl Poisson structure and Hamiltonian function.Through these analysis，we found that the motion of such rigid body with additional devices，under certain conditions，is stable.

special rigid body；stability；Poisson structure；Hamilton function；energy Casimir function

陈志贤 英文审校：张金顺，黄心中）

O 175.21；O 317

A

1000－5013（2012）02－0225－04

2011－06－17

梁建莉（1979－），女，讲师，主要从事哈密顿动力系统的研究.E－mail：liangjl＠hqu.edu.cn.

国务院侨办科研基金资助项目（08QZR10）