花岗岩石楼板的受弯性能试验

张楠，郭子雄

（华侨大学 土木工程学院，福建 厦门 361021）

花岗岩石楼板的受弯性能试验

张楠，郭子雄

（华侨大学 土木工程学院，福建 厦门 361021）

对10个单向受力石楼板的受弯性能进行试验，重点研究石板的受弯破坏形态、沿截面高度的应变分布规律和受弯承载力.试验结果表明：石板受弯破坏形态为完全脆性破坏，其受弯承载力主要受石板截面尺寸和石材天然缺陷所控制，存在一定离散型；石板断裂破坏前，横截面应变沿高度方向的分布基本上呈线性，符合平截面假定.基于平截面假定和试验结果统计分析，提出石楼板的受弯承载力计算公式，理论计算结果与试验结果吻合较好.

石结构；石楼板；脆性破坏；受弯承载力

石结构因其优越的耐久性、高强抗压强度和天然质朴观感，在我国许多地区，特别是福建沿海，仍有广泛应用［1］.虽然在福建省地方标准《石结构抗震设计规范》中规定“严禁采用石板、跨度大于1.2m的石梁和独立料石柱作为承载构件”，但石楼板在规范规定前已经大量存在，甚至迄今仍在福建沿海村镇使用，其安全性问题急需得到解决［2］.国内外有不少关于石墙抗震性能的相关研究报道［3－5］，也开展了采用改性砂浆－钢筋网片加固石板楼盖受弯承载力［6－7］，以及采用碳纤维增强塑料筋（CFRP）嵌埋加固石梁的研究［8］，但迄今仍未见任何有关石板楼盖受弯性能的研究报道.目前，闽东南沿海村镇的石结构房屋仍主要采用花岗岩石板和石梁的承载结构形式.由于石材存在天然裂隙，属脆性材料，当用作受弯构件时，往往受弯能力不足，冲击荷载下尤其容易脆断［2］.这些性能缺点使既有石结构房屋成为福建省当前最严重的地震安全隐患，亟需进行加固改造.因此，本文开展石板楼盖受弯性能的研究，以便于为石板楼盖的安全性鉴定和加固技术的研发提供理论依据.

1 试验概况

1.1 试件设计

为了研究石楼板的受弯性能，进行10个试件的试验，试件均选用闽南地区人工开采的花岗岩料石.试验得到的材料的物理力学性能：立方体试块和圆柱体试块的单轴抗压强度分别为128.5，101.8MPa；劈裂强度为8.3MPa；弹性模量为50.5GPa；数值均为平均值［6－7］.

石板为人工开采加工，材料的尺寸及制作工艺较为不统一，高为140mm，宽为420mm.将试件分为A，B两组，A组共选用4个试件，编号为A1～A4，共计2种跨度，进行三分点加载；B组共选用6个试件，编号为B1～B6，共计4种跨度，进行单点加载.两组10个试件的具体参数，如表1所示.表1中：跨度为l0；宽度为b；高度为h；l0／h为跨高比.

1.2 加载装置与测点布置

试验采用液压伺服作动器加载，加载采用三分点加载和单点加载两种加载方式（图1）.在正式加载前，先试加一级荷载，用以检查仪器的工作性能及消除接触面的空隙，然后卸除荷载并开始正式加载.正式加载采用分级加载，每级加载级差为1kN.

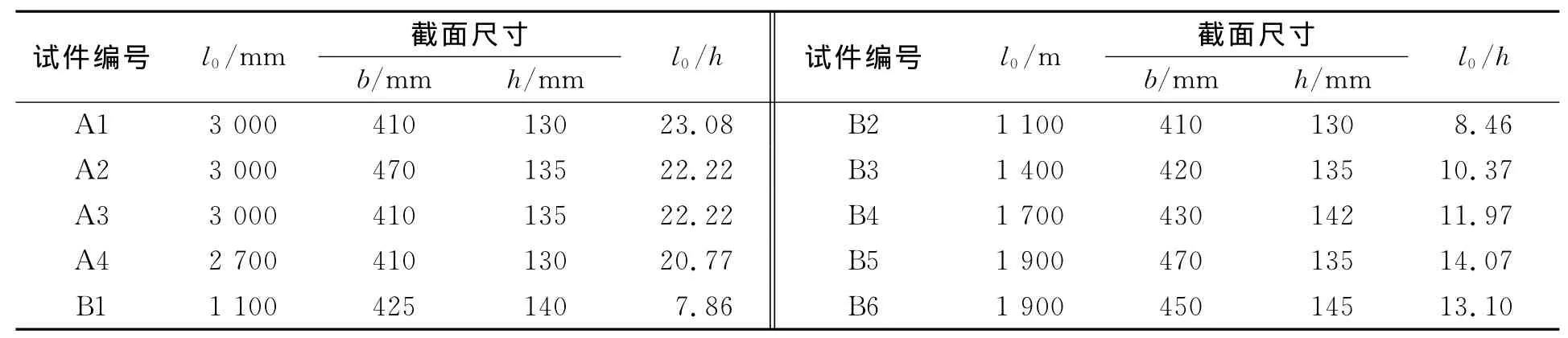
表1 试验参数Tab.1 Parameters of test specimens

在跨中截面沿板高等间距粘贴7个应变片，测量石板侧面的应变，同时测量板底、板顶应变；在板跨中、两个加载点下方和两个支座处放置位移计，以测量板底弯曲挠度和支座沉降，观察记录破坏形态.图2为板测点布置和位移计布置.试验数据由分散式数据采集器采集，采样频率为1Hz.

图1 加载方式装置图Fig.1 Test set－up

图2 应变片及位移计布置图（单位：mm） Fig.2 Arrangement of strain gauges and displacement meters（unit：mm）

2 试验结果及分析

2.1 破坏形态

所有石板均发生弯曲断裂破坏，试验现象基本相同.在加载初期试件基本无任何试验现象，随着荷载的增大，板底变形挠度缓慢增大.当荷载加到一定值时，石板在跨中附近开裂，并在瞬间整体脆断.断面基本呈一字型，断口较为整齐（图3）.荷载在裂缝初现时达到最大值.

以试件A4为例，荷载加至9.83 kN时，听到“嘭”一声，石板突然在一加载端断裂，石板分成两段，裂缝垂直于板面.破坏瞬间，板顶压应变达到最大为286με，远未达到石材的极限压应变，跨中位移最大达到3mm.破坏特征为弯曲断裂破坏，受压区石板抗压强度远小于石材极限抗压强度.

图3 试件破坏特征Fig.3 Failure pattern of specimens

2.2 石板荷载-跨中挠度曲线

各组试验石板跨中挠度试验结果，如图4所示.由图4可知：在试件达到最大荷载之前，试件的弯矩和挠度接近于直线变化；当试件达到最大荷载，承载力迅速下降.破坏时，弯曲变形较不明显，基本只能达到3mm左右.

从图4还可以看出，A组试件的极限弯矩较B组试件的小.这是由于三分点加载最大弯矩分布在试件较大的范围内，两个加载点之间无剪应力影响，处于纯弯状态；而单点加载时的最大弯矩发生在试件跨中横截面上，其受微缺陷影响的概率较三分点加载的要小得多.

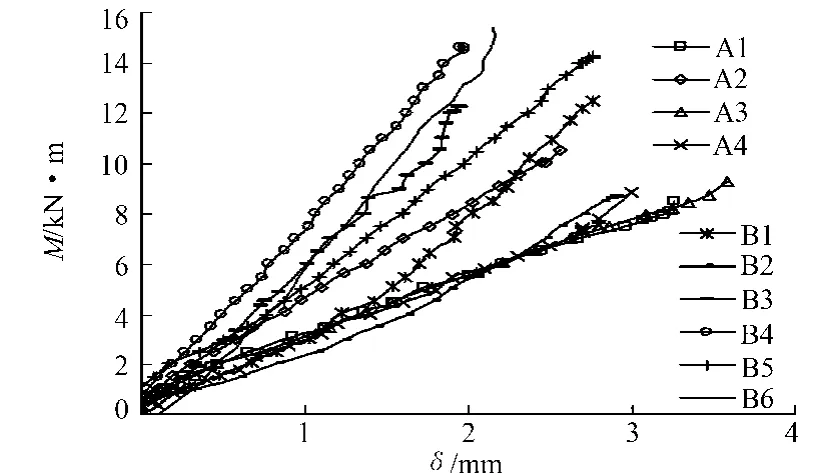
图4 弯矩－跨中挠度曲线Fig.4 Bending moment－mid span deflection curves of specimens

2.3 抗弯承载力分析

各试件的抗弯承载力试验结果，如表2所示.表2中：截面抵抗矩为W，开裂荷载为Pcr，开裂弯矩为Mcr.由表2可以看出：截面抵抗矩较大的试件，其极限承载力较高.说明对于纯石板受弯构件，相近跨高比条件下，控制设计的是截面抵抗矩.以试件A1与A3为例，A3仅比A1厚5mm，A3的抗弯承载力却比A1提高了9%.

表2 试件的抗弯承载力试验结果Tab.2 Summary of test results

2.4 截面应变分析

不同荷载等级下，典型试件（A2）跨中截面应变沿高度变化，如图5所示.从图5可以看出：在试件破坏前，石板横截面应变沿高度方向的分布基本上呈线性.因此，在石板进行受弯承载力计算时，平截面假定是成立的.从图5还可发现，截面中性轴的位置在加载过程中基本处于不变的位置，大约位于截面中部，平均离板底75mm.

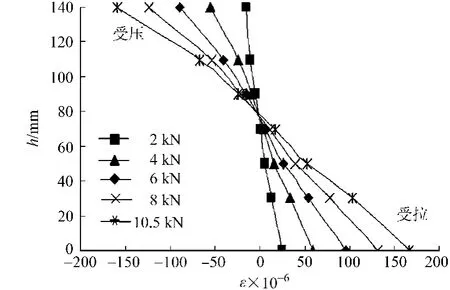
图5 A2跨中截面应变分布－荷载关系曲线Fig.5 Strain distribution－Load curve of the mid－span section

3 承载力简化计算

3.1 基本假定及公式推导

通过图6所示的截面应力与应变图形进行受力分析，认为当石板受拉边缘纤维应力达到石材的抗拉强度时，即宣告破坏.图6中：受压区高度为hc；受拉区高度为ht；板顶压应变为εc；板底拉应变为εt；板顶压应力为σc；板底拉应力为σt.

计算中作如下3点假定：1）试件符合平均应变平截面假定；2）石材为拉压各向同性线弹性材料，不考虑石材的各项异性对受弯性能的影响；3）试件承载力极限状态为受拉区达到材料抗拉强度.

由胡克定律可得：σc＝Ecεc，σt＝Etεt.根据力平衡条件，有

为了简化计算，假定石板在开裂前处于弹性阶段，满足平截面假定，其中性轴位于截面中心，则石板开裂弯矩的计算式为

式中：α为考虑石板截面加工误差、材料初始缺陷和开裂塑性的综合发挥系数，根据试验结果拟合得α＝0.95；ftu为石材抗拉强度，由材性试验得ftu＝8.3MPa；W 为截面抵抗矩，矩形截面W＝bh2／6.

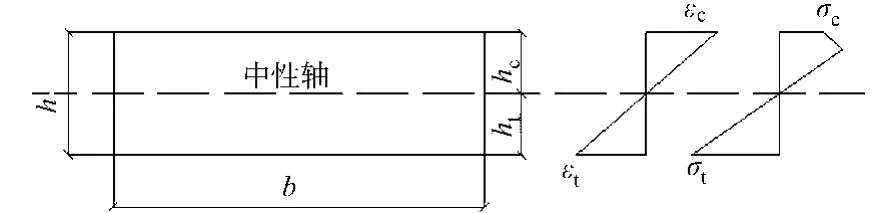
图6 石板截面的应力应变分布图Fig.6 Strain and stress distribution of the stone slab

3.2 理论分析与试验结果的比较

表3为计算得到的开裂弯矩（Mcr，c）与试验得到的开裂弯矩（Mcr，t）的对比.由于楔形效应的影响及试件材料的初始缺陷，单点加载条件下试件弯曲破坏并非发生在跨中，而是在跨中附近区域内，故表3中B组试件的试验弯矩为破坏截面的开裂弯矩，Mcr，c／Mcr，t的均值为0.98.由此可见计算与试验的结果较为吻合，理论计算方法能够反应试件的受力状态.

表3 开裂弯矩计算值与试验值对比Tab.3 Comparison of cracking moment between calculation and test results

4 结论

花岗岩石板试件一旦达到其开裂弯矩即迅速发生脆性断裂，断裂破坏面往往发生在最大弯矩区域的最小截面或有天然缺陷截面.板断裂破坏前，截面应变沿高度方向的分布基本上呈线性，受弯过程满足平截面假定.天然石材力学性能存在较大的离散型，在受弯承载力计算中，引入考虑石板截面加工误差、材料初始缺陷和开裂塑性的综合发挥系数，基本上能够反映材料离散性的影响.所提出的开裂弯矩理论计算结果与试验结果吻合较好.

［1］刘阳，郭子雄，杨勇，等.闽南地区农村住宅安全性现状及防灾建议［J］.华侨大学学报：自然科学版，2007，28（1）：63－67.

［2］郭子雄，黄群贤，柴振岭.石结构房屋抗震防灾关键技术研究与展望［J］.工程抗震与加固改造，2009，31（6）：47－51.

［3］郭子雄，柴振岭，胡奕东，等.条石砌筑石墙抗震性能试验研究［J］.建筑结构学报，2011，32（3）：66－72.

［4］郭子雄，柴振岭，胡奕东，等.机器切割料石砌筑石墙灰缝构造及抗震性能试验研究［J］.建筑结构学报，2011，32（3）：73－77.

［5］郭子雄，柴振岭，胡奕东，等.嵌缝加固条石砌筑石墙抗震性能试验研究［J］.土木工程学报，2010，43（S1）：136－141.

［6］王兰，郭子雄.石材受弯构件复合加固界面粘结性能试验［J］.华侨大学学报：自然科学版，2010，31（1）：78－82.

［7］郭子雄，王兰，柴振岭，等.钢筋网改性砂浆加固石楼板受弯性能试验研究［J］.建筑结构学报，2011，32（3）：78－83.

［8］刘阳，郭子雄，刘宝成，等.嵌埋CFRP筋组合石梁受弯性能试验研究［J］.建筑结构学报，2011，32（3）：84－88.

Experimental Investigation on the Flexural Behavior of Granite Stone Slabs

ZHANG Nan，GUO Zi－xiong

（College of Civil Engineering，Huaqiao University，Xiamen 361021，China）

10one－way stone slabs were tested to investigate the flexural behavior.The failure mode，strain distribution of cross－section and flexural bearing capacity of stone slabs were studied.The results indicate that the failure mode of stone slabs is brittle rupture；the control conditions of flexural capacity are the cross－section of stone slabs and natural defects of stone.Before the failure of stone slabs，cross－section strain distribution along the height is linear，and the plane－section assumption is valid.Based on the test results and the plane－section assumption，an analytical model is proposed to calculate the cracking moment of stone slabs.The proposed model agrees well to the experimental results.

stone structure；granite stone slab；brittle failure；flexural behavior

TU 578.102

A

1000－5013（2012）02－0184－04

2011－07－08

郭子雄（1967－），男，教授，主要从事工程抗震防灾的研究.E－mail：guozxcy＠hqu.edu.cn.

福建省自然科学基金资助项目（E0810021）；福建省厦门市科技计划项目（3502Z20093029）

（责任编辑：陈志贤 英文审校：方德平）