乌鸦悖论的“似然度比例测度”方案——与经典方案之比较

胡 浩

(华南师范大学公共管理学院，广东 广州 510006)

一、乌鸦悖论与亨佩尔解决方案

乌鸦悖论又称证认(confirmation)悖论或亨佩尔悖论。关于该悖论的解决在归纳逻辑和认识论研究中是一个根本性的问题。该悖论源于人们直觉上认为以下(1)，(2)，(3)原则都是合理的:

(1)Nicod标准:对于任意的对象a和谓词R(在本文特指乌鸦)和B(黑色的)，在无其他证据的情况下，Ra＆Ba证认∀x(Rx→Bx)，即P(∀x(Rx→Bx)/Ra＆Ba)＞P(∀x(Rx→Bx))。

(2)等值条件:对于任何命题H1，H2和E，如果E证认H1，而H1逻辑等值于 H2，那么E证认 H2。

(3)无关性条件:在无其他证据的情况下，┐Ra＆┐Ba与∀x(Rx→Bx)无关。即:P(∀x(Rx→Bx)/┐Ra＆┐Ba)=P(∀x(Rx→Bx))。然而，(1)，(2)，(3)是不一致的。因为，由(1)可得:┐Ra＆┐Ba证认∀x(┐Bx→┐Rx);进而与(2)一起可以推出:

(3)’在无其他证据情况下，┐Ra＆┐Ba证认∀x(Rx→Bx)。

显而易见，(3)和(3)’不能同时为真，这构成逻辑悖论。同时，(3)’意味着红帽子、白色的电话等既不是乌鸦又不是黑色的东西都可以证认“所有乌鸦都是黑色的”。这与人们对(3)的直觉相悖，形成直觉悖论。Patric Maher指出，如果要对该悖论给出完全令人满意的解决，需要满足如下三个条件。①P.Maher.Inductive logic and the Ravens Paradox，Philosophy of Science，1999，66:50－79。

(a)有令人信服的理由挑出以上(1)，(2)，(3)中哪个原则是错的。

(b)对于那个(那些)被认为是错误的原则，要给出解释它为什么是错误的。

(c)对于那个被认为是错误的原则，要能找到一个替换它的正确原则，但该替换原则充分地类似于错误的原则，以至于容易混淆二者，从而可以解释那个错误的原则为什么表面上是合理的。

亨佩尔对该悖论的解决是拒绝(3)而接受(1)和(2)，从而接受(3)’。

首先来看他的方案是否满足条件(a)。亨佩尔认为，等值条件对于任何恰当的证认标准都是必要的，否则是否某一证据证认某个假设依赖于假设的不同的(等值)形式。②C.G.Hempel.Studies in the Logic of Confirmation I＆II，Mind，1946，54:12。至于(1)，他则认为也许表达了一个特别明显而又重要的关于证认的充分条件，这使得他挑出的错误是(3)。但Nicod标准并非普遍有效，①Howson＆Urbach:Scientific Reasoning:The Bayesian Approach .Chicago:Open Court.1993:129、127。所以，他接受Nicod标准的理由并不充分。

为什么(3)直觉上是错误的?亨佩尔给出(3)’的独立论证。由于(3)和(3)’不能同时为真，既然可以给出(3)的论证，那么，有理由说(3)是错误的。亨佩尔论证如下:

如果证据E仅仅由一个…非黑的对象构成，那么E也许合理地被认为证认所有的对象是非黑的，更不必说，E支持较弱的断定所有非黑的是非乌鸦。②C.G.Hempel.Studies in the Logic of Confirmation I＆II，Mind，1946，54:20。

该论证承诺类似Nicod标准那样的证认关系，即┐Ra证认∀x┐Rx。另一方面，该论证还假定:(i)单调性条件，即E证认H，那么对于任意的X，E＆X也证认H;(ii)特殊后承条件，即E证认H，那么E证认H的所有逻辑后承。而(i)和(ii)两个条件都是为当代证认理论所拒绝的。③B.Fitelson.The Paradox of Confirmation，Philosophy Compass，2006:98。可见，亨佩尔的解决方案并非满足条件(b)。那么他的方案是否满足条件(c)呢?即如何来解释(3)为什么表面上是合理的?亨佩尔解释道，人们之所以得到(3)，并非是在重言证据下，而是相对于特定的背景知识:我们已知所观察到的对象a不是乌鸦。而对于一个已知不是乌鸦的对象，它不能提供任何关于乌鸦颜色的信息。④C.G.Hempel.Studies in the Logic of Confirmation I＆II，Mind，1946，54:20。即:

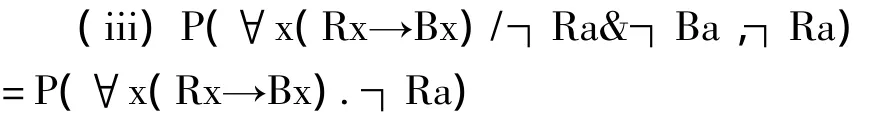
(iii)是符合直觉的一个原则。同时，(iii)也不与(3)’相悖，因为(3)’是相对于重言背景的。人们之所以认为(3)表面上是合理的，是因为混淆了(3)和(iii)。

以Maher的三个条件为判据，亨佩尔解决方案最恰当满足的是(c)，对(a)(b)条件的满足是有争议的，他的解决方案还不能完全令人满意。

然而，亨佩尔在分析悖论的直觉来源时，引入背景知识来进行分析，则是为当代贝叶斯主义者所欢迎的。但大多数当代贝叶斯主义者并不承认有相对于重言背景知识的概率，而是持认识论概率观。认识论概率是指相对于某些(实际的)非重言的背景知识的概率。证认关系不仅仅是理论和证据之间的关系，而是假设、证据和实际的背景知识三者之间不可还原的关系。

二、标准贝叶斯方案:豪森－厄巴赫方案

几乎所有的贝叶斯主义者都接受(3)’而拒绝(3)。例如，当今贝叶斯主义的代表科林·豪森(Colin Howson)和皮特·厄巴赫(Peter Urbach)在他们的经典著作《科学推理:贝叶斯方法》(1993)中谈到乌鸦悖论时，就曾指出:

事实是Ra＆Ba以及┐Ra＆┐Ba都证认假设H，但并非意味着它们具有相同的证认度。而一旦意识到证认是度方面的事情，这个结论(3)将不再是反直觉的，因为它与┐Ra＆┐Ba证认H(尽管它的证认度可以忽略)是协调的。这一简单的观点构成贝叶斯主义对这一问题的解决。⑤Howson＆Urbach:Scientific Reasoning:The Bayesian Approach .Chicago:Open Court.1993:129、127。

他们的这一论断隐含着如下两个论题:

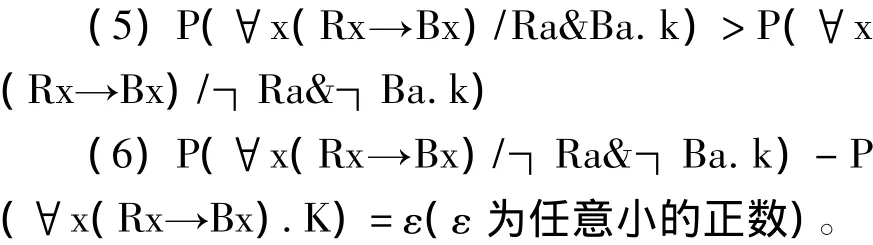
前一个论题称为“比较论题”，即黑乌鸦对假设的证认度要大于非黑的非乌鸦对假设的证认度。后一论题称为定量论题(该命题衍推(3)’，即由定量命题可以衍推出:非黑的非乌鸦证认“所有的乌鸦都是黑色的”这一假设，尽管这个证认度是极其微弱的)。如何论证这两个论题成为贝叶斯方案的基本问题。

我们首先来看，假如这两个论题是真的或可靠的，他们的解决方案是否满足Maher提出的(a)(b)(c)三个判据。首先解释为什么(3)表面上是合理的?(5)表明Ra＆Ba对假设H的证认度要大于┐Ra＆┐Ba对H的证认度，因而┐Ra＆┐Ba对H的证认度是相对小的。(6)则进一步表明┐Ra＆┐Ba对H的证认度可以忽略，这也解释了直觉悖论的来源是对(6)和(3)的混淆。另外，(5)或(6)是否能解释(3)是错误的或(3)’直觉上是正确的呢?只要能够说明定量命题(6)，那么就可说明(3)’是正确的。可见，要满足Maher的所有判据，(5)和(6)两个论题是关键。

为了讨论方便，我们以下用“H”表示“∀x(Rx→Bx)”。至于证认度(c)测度，通常有如下几种:

差异测度:d(H，E/K)=P(H/E.K)－P(H/K)

(对数)比例测度:r(H，E/K)= log(P［H/E.K］/P(H/K)

(对数)似然度比例测度:l(H，E/K)=log(P(E/H.K)/P(E/┐H.K)

规范化差异测度:s(H，E/K)=P［H/E.K］－ P(H/┐E，K)

除第四种测度外，前三种测度都满足如下我们希望的结果:

如果 P(H/E1.K)＞P(H/E2.K)，那么 c［H，E1/K］－c［H，E2/K］。①B.Fitelson.The Paradox of Confirmation:105。

豪森－厄巴赫在解决乌鸦悖论时，采用的是(对数)比例的测度。基于豪森－厄巴赫对“比较命题”和“定量命题”的相关论述，重构证明如下:

［3］P(Ra＆Ba/H)=P(Ba/H＆Ra)P(Ra/H)=P(Ra/H)=P(Ra)②第一个等式是根据贝叶斯定理，第二个等式是因为P(Ba/H＆Ra)=1。最后一个等式才是一个假设，即假定H对一个对象是乌鸦的认识论概率没有影响。(假设)……………

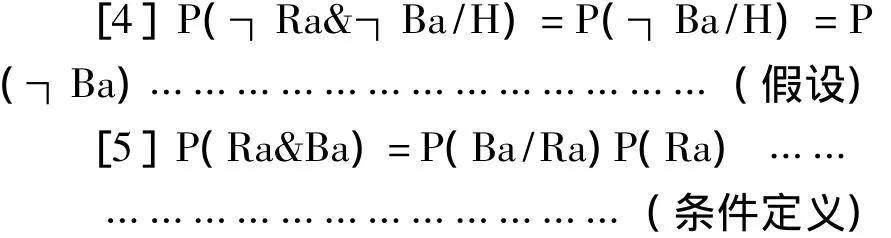
［6］P(Ba/Ra)=∑P(Ba/Ra＆θ)P(θ/Ra)=∑P(Ba/Ra＆θ)P(θ)= ΣθP(θ)(全概率定理，θ独立性假设③θ表示在宇宙中的乌鸦是黑色的可能的比例，可以是无穷多种可能性。θ独立性假设:P(θ/Ra)=P(θ)。而主要原则是指:P(Ba/Ra＆θ)=θ，即如果在宇宙中乌鸦是黑色的比例是θ，那么任何一个乌鸦是黑色的概率也为θ。，主要的原则)

以上证明序列中的［11］为定量命题，［14］为比较命题。比较命题的确立依赖于定量命题的确立，而定量命题的确立独立于比较命题。从以上的证明可以看出，为了建立命题［11］和［14］，他们提出如下四个背景假设(依证明序列中的编号):

相对于我们的实际背景知识［9］和［11］都是恰当的，而［3］和［4］则是有争议的。Varanas(2004)讨论过［4］的合理性问题。为了说明定量命题，他与标准方案的进路有所不同，引入的是差异测度:

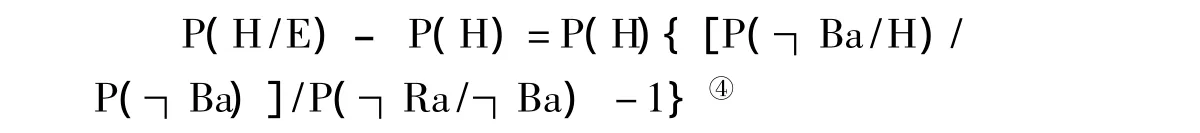
该公式中的 E=┐Ra＆┐Ba，H=∀x(Rx→Bx)。E对H的证认度由P(H/E)–P(H)测度。要得到定量命题，根据我们的背景知识［9］P(┐Ba/K)≥P(Ra/K)，那么，P(┐Ra/┐Ba)=1－ε。为保证 ε ＞{［P(┐Ba/H)/P(┐Ba)］/P(┐Ra/┐Ba)－1}＞0 ，P(┐Ba/H)/P(┐Ba)要大于1－ε，并接近1，即［4］’P(┐Ba/H)/P(┐Ba)≈1，这是类似于［4］的独立性假设，它的合理性在经典的贝叶斯框架下是没有得到过充分说明的。总之，无论在差异测度还是比例测度下，贝叶斯方案在建立定量命题时都须假定［4］，⑤在建立比较命题时都须假设［3］。而这个假设并不令人信服。Varanas论证，我们既无充分理由认为P(┐Ba/H)和P(┐Ba)一定会不一样，也无充分理由认为它们应该保持一致⑥也许人们会以为可以基于(条件)无差别原则论证该等式，但Varanus进一步论证表明条件无差别原则像经典无差别原则一样会导致不一致。。因此，基于这一假设的(5)和(6)两个论题仍是不可靠的。

另外，在豪森－厄巴赫的解决方案中是承诺了Nicod标准的。因为Nicod标准(1)是(5)和(6)的一个推论，但他们意识到Nicod标准并非普遍有效。他们以斯温伯(Swinber)的例子来说明Nicod标准的失效情况。被检验假设为“所有蚂蚱都在约克郡以外”，这时，假定在约克郡边界外面一点点发现一只蚂蚱，根据Nicod标准，这只蚂蚱证认以上假设。但假定边界并无特定障碍，观察到该蚂蚱，则否证了被检验假设。①Howson＆Urbach:Scientific Reasoning:The BayesianApproach.Chicago:Open Court.1993:129。Nicod标准并非普遍有效，而该方案却承诺它，这便使得该方案的普遍性受到进一步的限制。可见，对于贝叶斯方案来说，关键的困难是:是否有办法不依赖于［3］和［4］这样的独立性假设来确立比较命题以及定量命题，而又不承诺Nicod标准?Fiteson和Hawthorne(2006b)的“似然度比例测度”方案就是在这一背景下提出的。他们首先建立比较命题，并在比较命题的基础上建立定量比较命题，最后确立定量命题。这一进路和标准方案恰好相反。

三、“似然度比例测度”方案

Fitelson等采用的是“似然度比例测度”来考察证据和假设之间的相关度或证认度，他首先建立了如下等值关系:

P(H/Ra＆Ba.k)＞P(H/┐Ra＆┐Ba.k)iff P(Ra＆Ba/H.K)/P(Ra＆Ba/┐H.K)＞ P(┐Ra＆┐Ba/H.K)/P(┐Ra＆┐Ba/┐H.K)②B.Fitelson，J.Hawthorne:How Bayesian Confirmation Theory Handles the Paradox of Ravens，in E.Eells and J.Fetzer.Probabiity in Science，Chicago:Open Court.2006:23，25－29。

这样就将原来比较命题的合理性问题转换为“似然度比例”(likelihood－ratios)比较命题的合理性问题。在这里所谓“合理性问题”是指:在什么样的恰当条件下比较命题成立。这些条件又称非平凡性假设(non-triviality assumptions)(以下简称NA)，它们是一些非常弱且合理的假设:

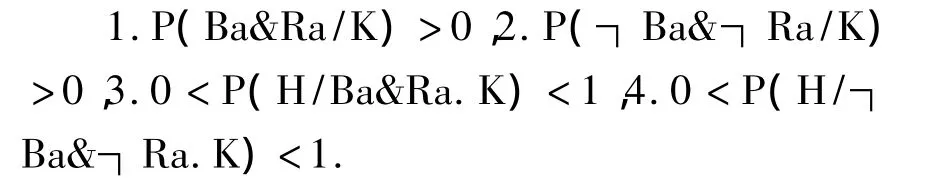
为了方便讨论，有如下定义:

在NA假设下，有如下定理和引理:

定理1:如果NA，那么有

引理:如果NA，那么有

1.3 D ＞1 iff［A－(1－C)］＞(C×B)⑤B.Fitelson，J.Hawthorne:How Bayesian Confirmation Theory Handles the Paradox of Ravens，in E.Eells and J.Fetzer.Probabiity in Science，Chicago:Open Court.2006:23，25－29。

引理给出的就是“似然度比例”比较命题成立的一般条件，即给出了一只黑色的乌鸦对假设H的支持度要高于一只非黑的非乌鸦的一般条件。从这些一般条件能够抽出符合直观的具体假设。首先，假定A=B，那么这条引理隐含着 D＞1 iff A或B＞1。这是说，无论假设H为真或为假，根据我们的实际知识，非黑的东西都比是乌鸦的东西多，则D＞1。注意这一结论的得出，同时依赖的是这样两个条件:

(1.3.1)是非常合理的假说。至于条件(1.3.2)，则要弱于［3］和［4］的合取(因为［3］和［4］衍推(1.3.2))。同时，(1.3.1)和(1.3.2)的适用范围要广于［3］［4］适用的范围，因为在［3］和［4］不成立的情况下，即当P((┐Ba/┐H.K)/P(┐Ba/H.K)大于1 时，只要 P(Ra/┐H.K)/P(Ra/H.K)同样程度(协变地)大于1，我们仍然可以得到D＞1的结果。但是，这二者之间的协变关系又如何确定呢?有什么理由认为二者会是同等程度协变的呢?。可见，条件(1.3.2)仍是一个存疑的假设。那么，是否存在替换(1.3.2)的合理条件而仍使得D＞1?Fitelson等建立如下定理:

假定 NA，如果 P［H/Ra.K］≥P(H/┐Ba.K)，并且(1.3.1)成立，那么 D ＞1。③B.Fitelson:The Paradox of Confirmation，Philosophy Compass，2006，p108 。

该定理的前件是一个较合理的假设。它说的是，对于“所有乌鸦都是黑色的”这一假设而言，一个是乌鸦的东西对该假说的证认度不会小于一个非黑的东西，应该说这一假设至少比［3］和［4］的合取要弱。这样，Fitelson建立的比较命题相对于标准方案来说，确有实质性的提高。

四、定量比较命题及其批判

有趣的是，为了建立定量命题，Fitelson尝试在比较命题的基础上进一步回答这样的问题:一个黑色的乌鸦对“所有乌鸦都是黑色的”这一命题的证认度比一个非黑并且是非乌鸦的东西对该假设的证认度究竟大多少?也就是说，他将建立一个定量的比较命题，该命题由如下定理给出。

定理2:如果NA，同时如下条件成立:

B=P(┐Ba/H.K)/P(Ra/H.K)≥ L＞1

即:B≥L＞1

A=P(┐Ba/┐H.K)/P(Ra/┐H.K)≈B，

即:对于某些大于0，但趋近于0的δ，有:

0＜1－δ≤A/B≤1+δ。

那么有如下结果:

2.1 ［(1－δ)－(1－C)/L］(1/C)＜D ＜(1+ δ)(1/C)。

2.2 如果L＞ ＞1，正数 δ趋于0，那么 D≈1/C。①B.Fitelson，J.Hawthorne:How Bayesian Confirmation Theory Handles the Paradox of Ravens:28－29。

以上定理说的是，一只黑乌鸦对假设“所有乌鸦都是黑的”的证认度与一个非乌鸦并且是非黑的对象对“所有乌鸦都是黑色的”的证认度之比约为1/C。因0＜C＜1，所以，D不仅大于1，而且约等于1/C。这就是Fitelson建立的定量比较命题。在此基础上，Fitelson给出如下定理以确立定量论题得以成立的必要条件。

定理3:如果NA，并且满足如下条件:

3.1 B ＞A ＞1

3.2 A≈B，即(1－δ)≤A/B≤(1+δ)

3.3 1－ε≤P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］≤1+ε

那么，P［Ba＆Ra/H.K］/P［Ba＆Ra/┐H.K］=(1+－δ)(1+－ε)P［Ba/Ra.H.K］/P［Ba/Ra.┐H.K］≈1/C。②其中 P［Ba/Ra.H.K］/P［Ba/Ra.┐H.K］=1/C。

该定理表明，┐Ba＆┐Ra对H的证认度在以0为中心的一个极小区间内变化的必要条件是P［Ba/Ra.H.K］/P［Ba/Ra.┐H.K］≈1/C 。另外，这一定理允许┐Ba＆┐Ra对假设H的支持度可以为0(当ε=0)，有微弱的支持或有微弱的否证度(当ε＞0)。所以，这一定量命题比原来的定量命题适用范围要宽。要注意的是3.3并非是标准的定量命题，③事实上，关于 P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］和 P［H/┐Ba＆┐Ra.K］/P［H.K］的断定(标准的定量命题是关于后面这个比例的断定)并非完全等值，但二者存在有衍推关系，前者衍推后者。但3.3将衍推弱化的标准定量命题。④证明:(1)P(H∨┐H/┐Ba＆┐Ra.k)=P(H/┐Ba＆┐Ra.k)+P(┐H/┐Ba＆┐Ra.k)=1={P(H/K)P［┐Ba＆┐Ra/H.K］+P(┐H/k)P［┐Ba＆┐Ra/┐H.K］}/P(┐Ba＆┐Ra.k)≈P［┐Ba＆┐Ra/H.K］/P(┐Ba＆┐Ra/.k)≈1(因为 P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］≈1)，(2)P［H/┐Ba＆┐Ra.K］=P(H/.K)P［┐Ba＆┐Ra/H.K］/P(┐Ba＆┐Ra.K)≈P(H/K)(因为 P［┐Ba＆┐Ra/H.K］/P(┐Ba＆┐Ra/.k)≈1)总之，在建立定量命题的必要条件中，不需要独立性假说，也不必一定承诺Nicod标准，从而避免了经典贝叶斯方案的缺点。

人们之所以相信┐Ba＆┐Ra对H的证认度为0，是因为他们错误地将 P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］≈1 与 P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］=1混淆了。而标准方案则会解释为是因为人们把微弱证认度忽略了，但这一解释依赖于前面提到的独立性假设。如果独立性假设是错误的，他们将要改变解释。目前来看，独立性假设的合理性是不能有力辩护的。

进一步的问题是，1－ε≤P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］≤1+ε得以成立的充分条件是什么呢?Fitelson并没有给出，但在其方案中隐含着这样的结果。定理(2)告诉我们，{P［Ba＆Ra/H.K］/P［Ba＆Ra/┐H.K］}/{P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］}≈1/C(当 B ＞＞1 时)，假如 P［Ba＆Ra/H.K］/P［Ba＆Ra/┐H.K］≈ 1/C，那么 P［┐Ba＆┐Ra/H.K］/P［┐Ba＆┐Ra/┐H.K］≈1，同时可得到弱化的标准形式的定量命题 P［H/┐Ba＆┐Ra.K］≈P(H/K)。可见定理 3不仅给出了3.3的必要条件，还给出了它的充分条件。

相比标准方案，“似然度比例测度”方案基于较弱的假设建立了较弱的定量命题，因此没有承 诺Nicod标准。总的来看，该方案确有资格称为标准方案的提高版本。然而，该方案在建立定量比较命题时，无论在定理2还是在定理3中，都假定了A≈B(它类似于条件(1.3.2))，尽管它弱于［3］和［4］的合取，却并未得到进一步辩护。可见，如何基于更合理的假设来证明定量命题，仍是贝叶斯证认理论的一个课题。