角向偏振光束大数值孔径透镜聚焦的偏振开关现象

田博，蒲继雄

（华侨大学 信息科学与工程学院，福建 厦门 361021）

角向偏振光束大数值孔径透镜聚焦的偏振开关现象

田博，蒲继雄

（华侨大学 信息科学与工程学院，福建 厦门 361021）

利用Richards－Wolf矢量衍射积分模型，推导双环角向偏振光束经过环状高数值孔径透镜聚焦后聚焦区域的偏振特性，并用数值计算分析各相关参数的取值变化对焦面光斑的偏振分布的影响.研究表明：双环角向偏振光束经过环状高数值孔径透镜聚焦以后，其光斑内环的偏振方向发生改变；通过控制各相关参数的取值，可以控制聚焦光斑的偏振分布，形成一种可控的偏振开关.

双环角向；偏振光束；高数值孔径；偏振开关；Richards－Wolf衍射积分

Richards和Wolf提出矢量衍射积分公式对激光束经过高数值孔径透镜的聚焦进行研究以后，已有不少学者对各类光束的深聚焦特性做了大量的研究［1-5］.当激光光束经高数值孔径透镜聚焦后，会得到一个比普通聚焦小得多的光斑 .因此，这种聚焦可以广泛应用于平版印刷术、光数据存储、信息编码、粒子束囚禁及数据处理等方面［5-6］.许多学者对径向偏振和角向偏振光束的产生和应用进行了大量的研究［7-13］.K.S.Youngworth等［7］研究了径向偏振和角向偏振光束经过高数值孔径透镜聚焦的聚焦特性，结果表明径向偏振光束经高数值孔径聚焦后，产生一个很强的纵向光长分量和比普通聚焦更小的光斑，角向偏振光束聚焦后轴上光强始终为零 .然而，到目前为止，对于双环角向偏振光束经过环状高数值孔径透镜聚焦后，其光束特性的偏振特点还没有系统的研究.本文基于Richards－Wolf衍射积分理论，研究光束经过环状高数值孔径透镜聚焦以后再焦平面附近的偏振特性的变化，讨论光束的相关参量及高数值孔径透镜的孔径大小对该光束偏振的影响.

1 理论分析

图1为双环角向偏振光深聚焦几何光学示意图.根据Debye理论，假设双环角向偏振光束经过拦截比为δ的高数值孔径透镜聚焦，则聚焦后的光场［7］表示为

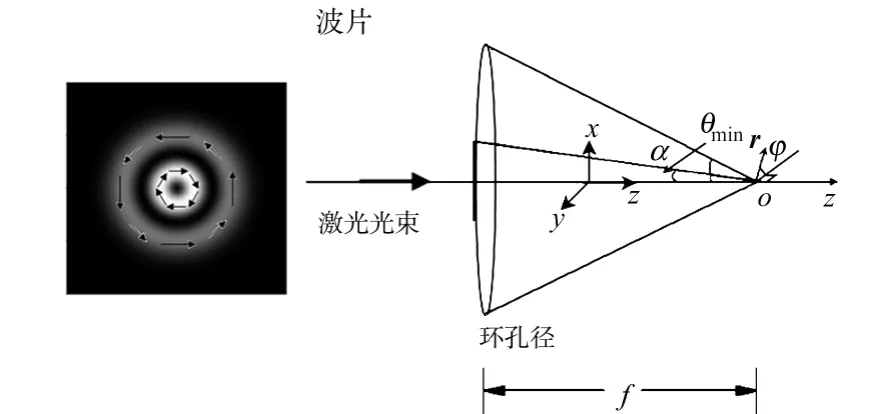
图1 双环角向偏振光深聚焦几何光学图Fig.1 Geometric scheme of tight focusing of a double－ring－shaped azimuthally polarized beam

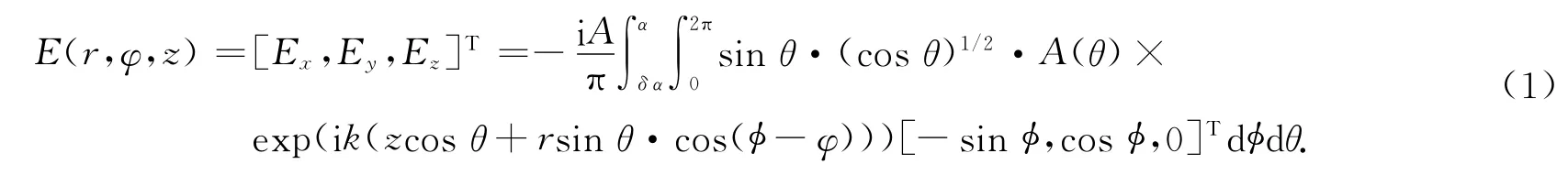
式（1）中：r，φ和z为场平面上观察点的柱坐标表示形式；α＝sin（NA）是由数值孔径NA决定的最大数值孔径角；δ为内聚焦角θmin与最大孔径角α的比率；k＝2π／λ为波矢；A（θ）是光场在透镜光阑面的瞳孔切趾函数.

根据文献［7］的公式，即

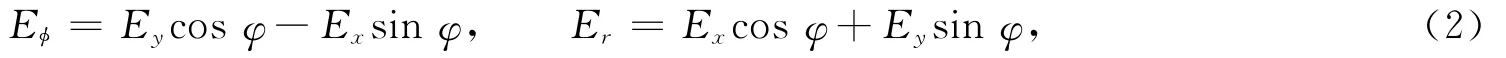
可以得到

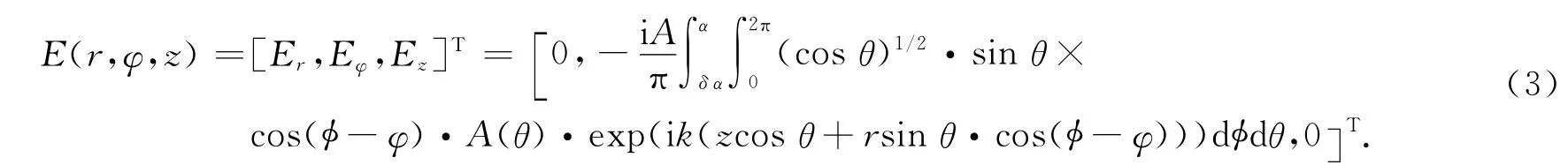
利用文献［7］公式，即

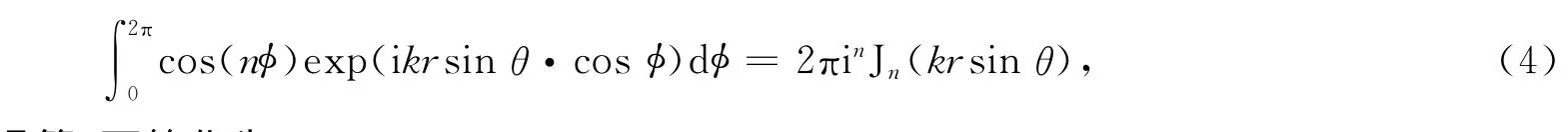
并经过复杂的积分运算，可简化为

以拉盖尔－高斯光束为研究模型，其角谱形式的光瞳切趾函数［7，14-15］可以表示为

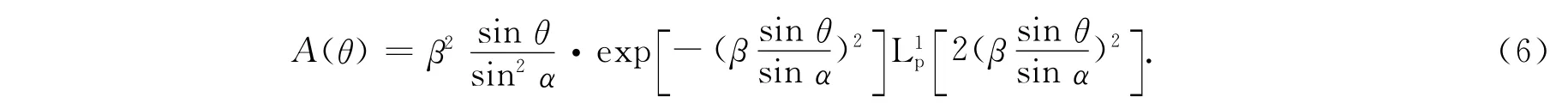
式（6）中：L1p是广义拉盖尔多项式，利用拉盖尔高斯分布可以得到p＋1个环（p为径向模数）；J1为一阶Bessel函数；β为物镜前由光瞳半径与入射光腰的比率决定的入射光的参数，且β＞1，如果β≤1，则光瞳完全阻挡了双环角向光束的外环.

将式（6）代入式（5）中，计算3个正交方向的光强 .由式（6）可知，双环角向偏振光束经过环状高数值孔径透镜聚焦后，其径向方向和纵向方向分量为零，角向方向分量的光强即为总光强.基于上述推导的光强公式进行数值模拟，就可以研究双环角向偏振光束经过环状高数值孔径透镜聚焦的偏振特性.

2 数值模拟

角向双环角向偏振光经过环状高数值孔径聚焦以后在焦平面上的偏振分布和电场分布，分布如图2，3所示 .计算参数：激光光束波长λ＝633mm；折射率n＝1；β＝1.2；NA＝0.6；p＝1；横坐标r和纵坐标z均归一化为λ的倍数.

由图3（a），（b）可以看出，当δ＝0时，由于角向偏振经环状高数值孔径聚焦以后只有角向分量，所以聚焦后光斑为角向偏振正方向如图2（a）所示，即与入射光内环方向相同，图1所示的顺时针方向；而当δ为0.750时，光斑内环为角向偏振逆方向如图2（b）所示，即与入射光内环方向相反，图1所示的逆时针方向.这可能是由于环状透镜挡住部分内环光强，使双环角向光束部分光强聚焦的结果.

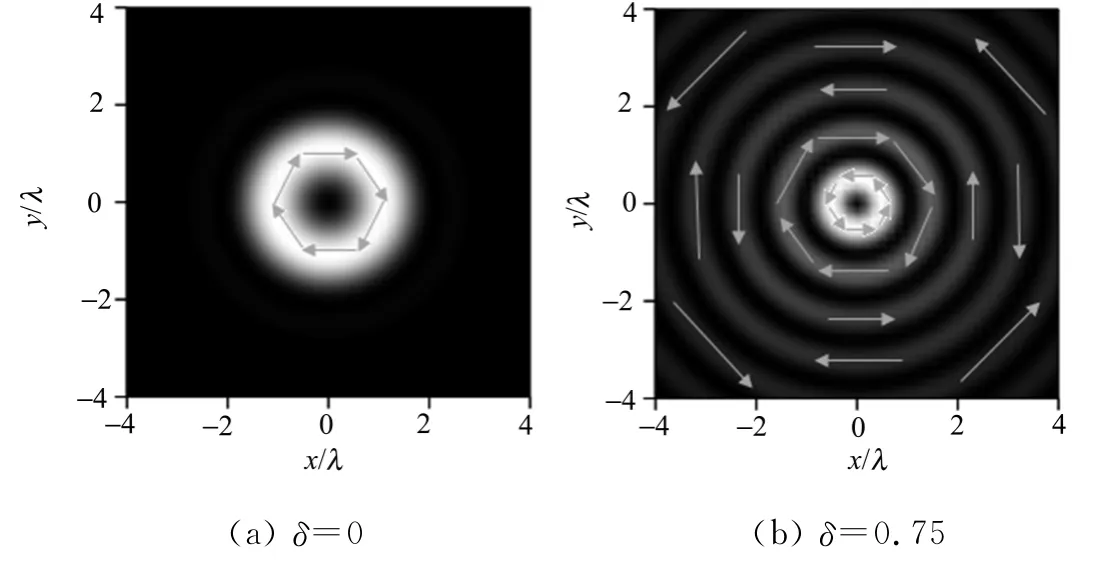
图2 在焦平面内聚焦光斑的偏振分布Fig.2 Polarization distribution of the focal hole in the focal plane

由图3（c）～（e）可看出，随着δ的减小，内环的偏振方向发生明显的变化.当δ为0.580时，其内环偏振方向（逆时针方向）与入射光内环偏振方向相反（顺时针方向）；而当δ为0.588，0.700，其内环偏振方向开始逐渐与入射内环方向相同.δ为0.588即为偏振方向改变的临界值.

聚焦后，内环偏振方向由逆时针方向变为顺时针方向因此可在β＝1.2，NA＝0.6的情况下，通过控制δ的大小来控制内环的偏振方向，来产生偏振开关的现象.

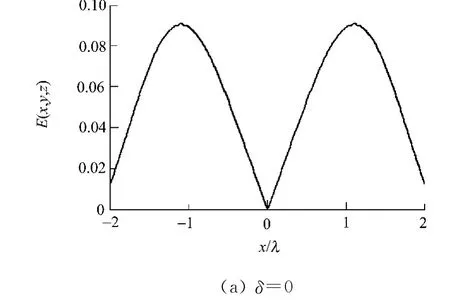
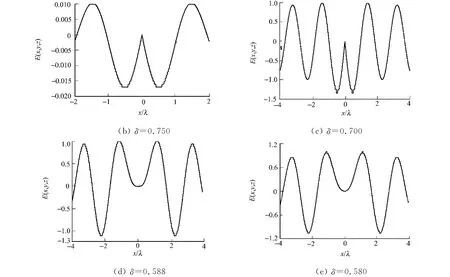
图3 在焦平面内聚焦光斑的电场分布Fig.3 Electric field distribution of the focal hole in the focal plane

双环角向偏振光经过环状高数值孔径聚焦以后，其偏振变化临界值δ′随数值孔径NA和参数β的变化关系，如图4所示.

由图4（a）可看出，无论是β＝1.2或β＝1.3的情况，聚焦以后的偏振变化临界值δ′都是随NA的增大而减小，并且在数值孔径很大的情况下其减小速度增快.另外可以发现，无论NA取何值时，β＝1.2的临界值都大于β＝1.3.

从图4（b）可看出，当参数β逐渐增大的情况下，偏振变化的临界值δ′逐渐减小，由此可以在NA与其他参数不变的情况下，通过控制参数β的大小，来控制偏振的改变，即形成一种可控的偏振开关.经过计算，当参数β≥1.34时，聚焦光斑内环的偏振方向不会发生改变，始终与入射光内环偏振方向相反，不会产生偏振开关的现象.

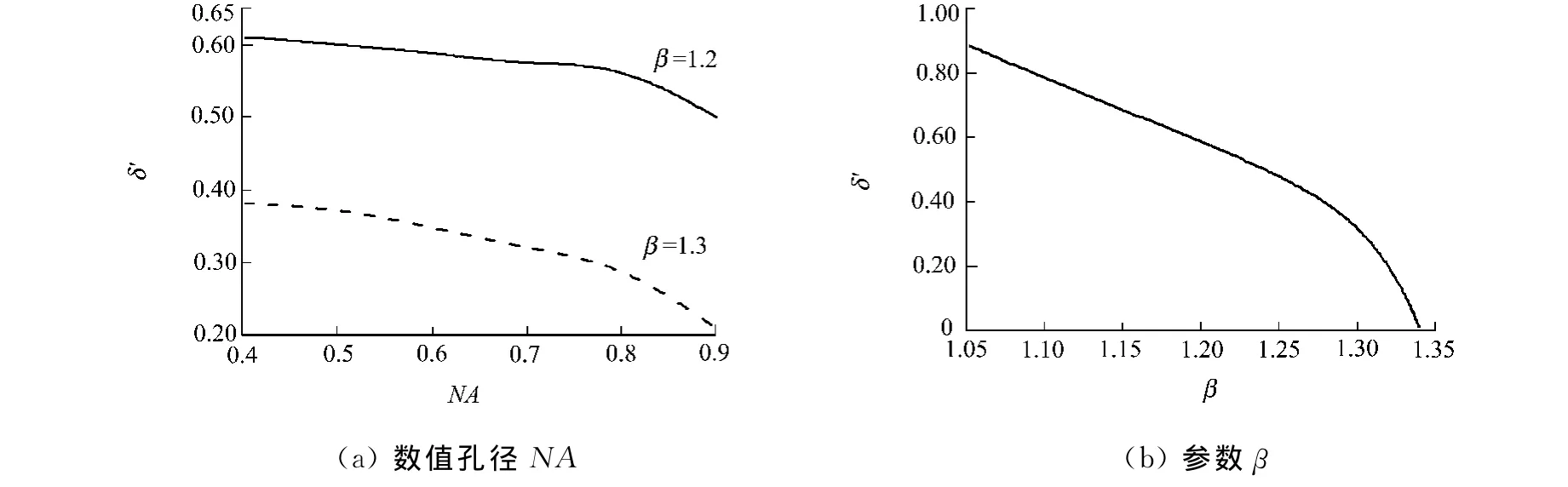
图4 偏振开关出现时的临界值δ′随NA和β的变化关系Fig.4 Critical valueδ′for occuring of polarization switch relating to NAandβ

3 结束语

基于Richards－Wolf的矢量衍射积分公式，研究双环角向偏振经环状高数值孔径透镜聚焦后聚焦区域的偏振特性.结果发现：双环角向偏振光束经过环状高数值孔径透镜聚焦以后，在焦平面产生的光斑的偏振方向随着相关参量的变化而发生变化 .研究结果对于双环角向偏振光束在信息编码等方面的应用有着重要的意义.

［1］张志明，蒲继雄，王喜庆.圆柱偏振贝塞耳－高斯光束经高数值孔径透镜的聚焦［J］.中国激光，2008，35（3）：401－405.

［2］陈宝算，蒲继雄 .部分相干圆偏振涡旋光束的深聚焦［J］.华侨大学学报：自然科学版，2011，32（3）：269－275.

［3］GROSJEAN T，COURJON D.Smallest focal spots［J］.Opt Commun，2007，272（2）：314－319.

［4］ZHAN Qi－wen，LEGER J.Focus shaping using cylindrical vector beams［J］.Opt Exp，2002，10（7）：324－331.

［5］LERMAN G M，LEVY U.Tight focusing of spatially variant vector optical fields with elliptical symmetry of linear polarization［J］.Opt Lett，2007，32（15）：2194－2196.

［6］HE H，FRIESE M E J，HECKENBERG N R，et al.Direct observation of transfer of angular momentum to absorptive particles from a laser beam with a phase singularity［J］.Phys Rev Lett，1995，75（5）：826－829.

［7］YOUNGWORTH K S，BROWN T G.Focusing of high numerical aperture cylindrical－vector beams［J］.Opt Exp，2000，7（2）：77－87.

［8］CIATTONI G，CIATTONI A，SAPIA C.Radially and azimuthally polarized vortices in uniaxial crystals［J］.Opt Commun，2003，202（1）：33－40.

［9］ZHANG Zhi－ming，PU Ji－xiong，WANG Xi－qing.Tight focusing of radially and azimuthally polarized vortex beams through a uniaxial birefringent crystal［J］.Appl Opt，2008，47（12）：1963－1967.

［10］ERDÉLYI M，BOR Z.Radial and azimuthal polarizers［J］.J Opt A：Pure ＆ Appl Opt，2006，8（9）：737－742.

［11］BOMZON Z，BIENER G，KLEINER V，et al.Radially and azimuthally polarized beams generated by space－variant dielectric sub wavelength gratings［J］.Opt Lett，2002，27（5）：285－287.

［12］KHOPTYAR D，GUTBROD R，CHIZHIK A，et al.Tight focusing of laser beams in aλ／2－microcavity［J］.Opt Exp，2008，16（13）：9907－9917.

［13］ZHANG Yao－ju，XU Xun，OKUNO Y.Theoretical study of optical recording with a solid immersion lens illuminated by focused double－ring－shaped radially－polarized beam［J］.Opt Commun，2009，282（23）：4481－4485.

［14］KOZAWA Y，SATO S.Sharper focal spot formed by higher－order radially polarized laser beams［J］.J Opt Soc Am：A，2007，24（6）：1793－1798.

［15］KOZAWA Y，SATO S.Focusing property of a double－ring－shaped radially polarized beam［J］.Opt Lett，2006，31（6）：820－822.

Polarization Switches Phenomena of Tight Focusing of an Azimuthally Polarized Beam Through a High Numerical Aperture Lens

TIAN Bo，PU Ji－xiong

（College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China）

By using the Richards－Wolf vector diffraction theory，the polarization properties in focused area of a doublering－shaped azimuthally polarized beam through an annular high numerical aperture lens are studied in this paper.Numerical calculations are performed to compare the influence of corresponding parameters on the tight polarization properties.It is shown that tight focusing of a double－ring－shaped azimuthally polarized beam can change the polarization direction of the inner ring in the focal field.The correlated parameters changed，the polarization direction shows gradual change and controllable polarization switch occurred.

double－ring－shaped azimuthally；polarized beams；high numerical aperture；polarization switches；Richards－Wolf diffraction integral

黄晓楠 英文审校：吴逢铁）

O 436

A

1000－5013（2012）03－0247－04

2011－05－13

蒲继雄（1962－），男，教授，主要从事光束传输与非线性光学的研究.E－mail：jixiong＠hqu.edu.cn.

国家自然科学基金资助项目（60977068）

book=204,ebook=204