双坡屋面低矮房屋风致内压的数值模拟

肖明葵，赵民，王涛

（1.重庆大学 土木工程学院，重庆 400045；2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045）

双坡屋面低矮房屋风致内压的数值模拟

肖明葵1，2，赵民1，王涛1

（1.重庆大学 土木工程学院，重庆 400045；2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045）

针对围护结构出现洞口后风致内压与外压联合作用这一造成建筑物严重破坏的主要原因，应用计算流体力学软件ANSYS Fluent 12.0，选用基于Reynolds时均的标准k－ε湍流模型，对低矮房屋单一主洞口及多洞口模型进行不同工况的数值模拟分析.结果表明：单一洞口工况下开孔率对风致内压影响很小，而开洞位置对各表面风致内压分布的影响显著；多洞口工况0°风向角时，平均内风压系数随着洞口面积比的增大而增大，但增大趋势逐渐变缓；纵墙和屋面同时开洞且开洞面积比一定时，结构平均内风压系数随风向角变化显著，且内压分布的不均匀性显著增强.

计算流体力学；双坡屋面；风致内压；数值模拟；湍流模型

国内外风灾调查数据表明，全球每年由于风灾造成的损失在100亿美元以上，其中由于低矮房屋损毁造成的损失占50%以上［1］；在国内，由于风致内压和外风压的联合作用，破坏最多的是围护结构及屋面体系［2－3］.Liu，Vickery，Stathopoulos，Holmes等［4－7］早在19世纪70年代就研究了围护结构突然出现洞口时，屋盖结构的瞬态动力响应和Helmholtz共振的影响.Woods等［8］通过风洞试验研究孔隙率和主洞口对非稳态和稳态阶段风致内压的影响，考虑了单一主洞口以及迎风面和背风面各开一个主洞口的情况，但是没有考虑风向角的影响.Beste等［9］研究了低矮建筑风致内压与平均外风压的相关性.Sharma等［10－11］对单一主洞口情况下围护结构柔度对风致内压和净风压的影响进行了研究，显示围护结构的柔度能降低Helmholtz共振频率并增大阻尼；此外，通过风洞试验对一缩尺模型进行了斜风作用下建筑存在单一主洞口时的Helmholtz共振现象的研究.在国内，楼文娟、卢旦、余世策等［12－14］对结构突然开洞后大跨屋盖的风致振动响应及内风压进行了研究.以上研究主要集中在开洞瞬间围护结构的动力响应和可能发生Helmholtz共振的情况，而流动达到稳态阶段后内风压规律则没有得到足够的重视，相应的研究较少.宋芳芳等［15］对稳态阶段洞口分布位置和数量变化，以及风向角等因素对内风压分布规律的影响进行了研究，但文中没有提及开孔率对内压分布的影响，并且在考虑多洞口工况时，其洞口分布较单一.因此，本文针对开孔率及单一洞口和多洞口工况对风致内压的影响进行数值模拟研究.

1 单一主洞口模型的数值模拟

目前研究结构风荷载方法主要有理论方法、现场实测和风洞试验3种.由于大气边界层中钝体绕流是非常复杂的，对于结构的风荷载，很难从流体力学理论上直接进行分析.风洞试验是目前公认较为准确的确定结构风荷载的方法.低矮房屋的全尺寸场地试验开展得较多，颇具影响的是美国德州理工大学风工程研究现场试验室（WERFL）的TTU建筑模型场地试验［16－18］.风洞试验和现场实测都存在着试验经费大、周期长的问题.随着计算机软硬件水平的飞速发展和计算流体动力学技术的不断完善，出现了与试验相对应的数值模拟方法，并已逐步成为继风洞试验后预测建筑物表面风压、周围风速和湍流特性的有效方法 .只要参数取得合理，数值模拟分析结果与理论计算值和文献［17－18］试验的实测结果可以较好地吻合.

1.1 几何建模及网格划分

基本厂房模型：特征尺寸（长（L）×宽（W）×高（H））为60m×21m×7.8m；单跨、双坡屋面；屋面坡度为5°；檐口高度为7.8m.计算流域分为外域和内域，其外域尺寸为260m×200m×60m，内域尺寸为50m×100m×30m［19］，内域网格加密处理.建筑物置于流域沿流向前1／3处，流域设置满足阻塞率小于3%的要求.

首先模拟0°风向角时的5种单一主洞口的工况.当一个洞口的面积大于背景孔隙泄露面积的2倍时，就可以把它定义为主洞口，主洞口处的外风压性质对于内风压的大小起着决定性的作用.5种洞口分别设置在强风中容易发生破坏的位置，其洞口的尺寸和位置如图1和表1所示.表1中：a为开洞率；洞口尺寸为宽（W）×高（H）.

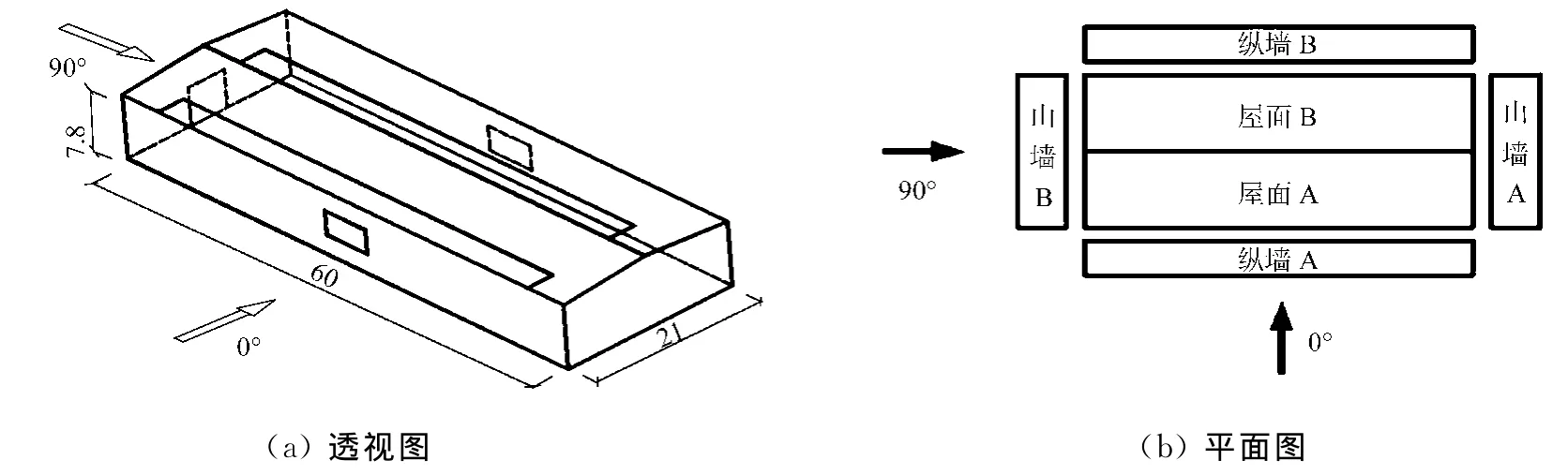
图1 双坡屋面厂房模型洞口位置及风向角示意图Fig.1 Model size and wind attack angle of plant house with gable roof

表1 双坡屋面厂房各模型信息Tab.1 Model′s information of plant house with gable roof

1.2 边界条件及参数的设定

速度进流边界条件采用指数率模拟大气边界层风速剖面［20］，即有

式（1）中：Z0为参考高度；U0为参考高度处风速，文中参考高度统一取10m［21］，U0＝12.8m·s－1；Z，U分别为流域中任意一点高度和其对应的平均风速；α为地面粗糙度指数，由于厂房多位于城市郊区或乡镇，故取B类地貌，α＝0.16.

出流面上采用完全发展出流边界条件，即流域顶部和两侧采用对称边界条件，等价于自由滑移的壁面；建筑物表面和地面采用无滑移的壁面条件.在风场模拟中，我国现行规范还没有明确的湍流度要求，文中对B类风场的湍流强度参考日本规范建议的湍流强度I取值［3，19，22］，即

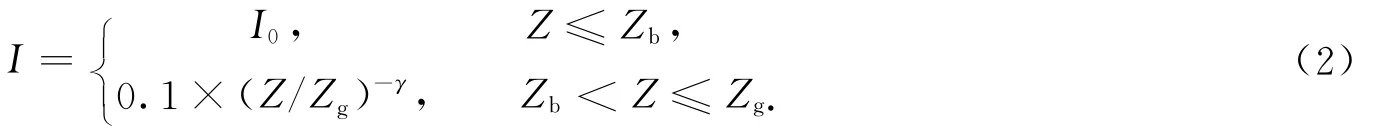
在B类风场下，式（2）中各符号取值如下：I0＝0.23；γ＝0.2；Zb＝5m；梯度风高度Zg＝350m.计算中，在进流处以直接给定湍动能k和湍流耗散率ε的方式给定入流处湍流参数，有

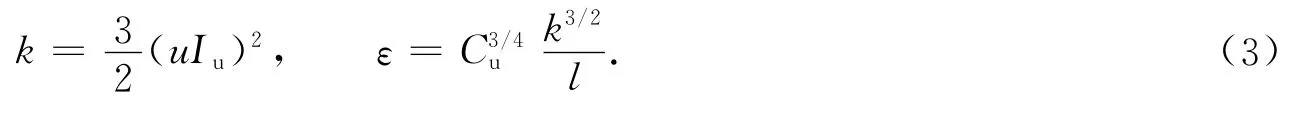
式（3）中：Cu＝0.09；湍流积分尺度l＝0.07L，L为建筑物的特征尺寸.

大气边界层风速剖面u、湍动能k和湍流耗率ε采用Fluent提供的UDF（user defined functions）编程与Fluent作接口实现.计算采用3D单精度，分离式求解器，空气模型选用不可压缩的常密度空气模型，对流项的离散采用精度较高的二阶迎风格式，速度压力耦合采用SIMPLEC算法，选用非平衡壁面函数模拟壁面附近复杂的流动现象.计算迭代收敛的标准为所有变量的量纲残差降至10－4以下.

1.3 数值模拟结果及分析

风压系数CP以10m高度处的流动压作为无量纲化的参考风压来计算，即有

式（4）中：¯P为平均风压；P0为参考风压；ρ为空气密度；¯Uh为参考高度处的平均风速.

1.3.1 开孔率的影响 以模型1为基准，仅改变纵墙开孔率，分别对开孔率为0.02，0.10，0.25，0.50和1.00等5种工况进行模拟.分析结果表明：纵墙开洞大小对模型各面平均内风压系数影响较小；内风压系数在0.70～0.75之间波动，且在各个面分布均匀；外风压系数几乎不随开洞面积大小的变化而变化.说明在单面开洞情况下，开洞的大小对模型周围流场的影响较小，对建筑内外表面的平均风压的影响是可以忽略的.

1.3.2 不同开洞位置的模拟 由于开孔率对建筑内外表面的平均风压的影响很小，因此对表1中开洞位置不同的各模型进行数值模拟，并将结果与封闭模型数值模拟结果做对比分析，如表2所示.表2中：净风压系数等于外风压系数与内风压系数之差.

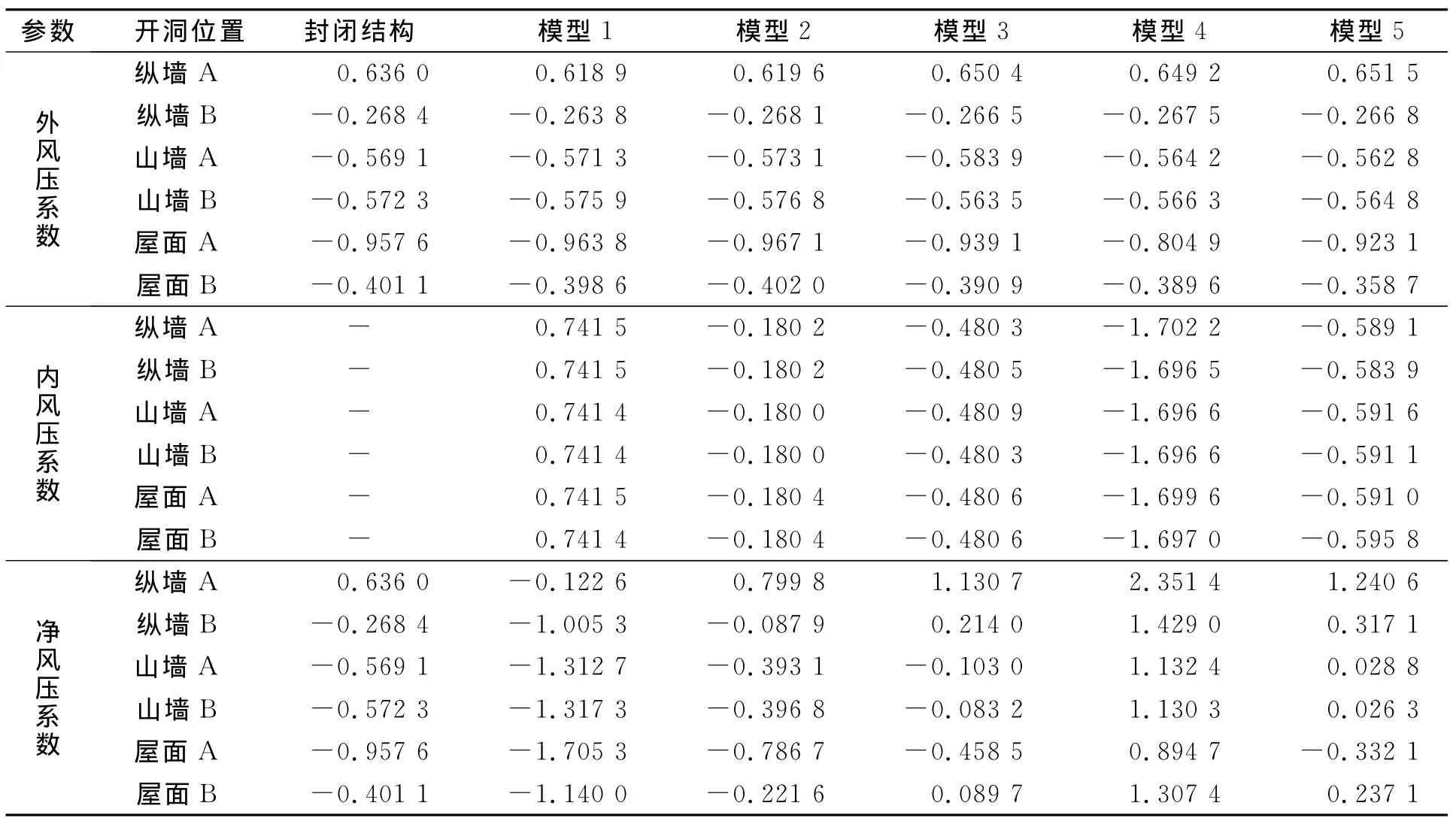
表2 0°风向角时模型各面风压系数模拟结果Tab.2 Simulation results of pressure coefficients of models at wind attack angle 0°

从表2可以看出：模型各面的风致内压分布都很均匀，平均风压系数相差很小，所以可以用一个平均内风压系数来表示整个结构的风致内压.0°风向角时，5种开洞位置中不利情况出现在模型1和模型4，迎风纵墙开洞时除迎风纵墙本身外，其余各面的净风压系数相对于封闭结构外表面风压系数均增大两倍以上 .屋檐处开洞时内风压系数相对其他几种工况十分突出，这是由于屋面坡度较小时，来流在屋檐处由于漩涡脱落形成负压极值区，最终导致结构各面承受较大的正压力 .这不会导致围护结构被风吹跑等破坏，但仍应考虑其与恒载共同作用时的不利影响 .此外，其他3种开洞位置模型均降低了除迎风纵墙外各面的风压系数.

表2同时表明：开洞对模型各面外风压分布影响较小.从结构内、外压平衡的角度看，表面开一个主洞口时，内外气压在达到平衡后，内部气流几乎没有流动，则内部压力处处相等，且等于洞口处风压.内、外压的这种平衡作用使模型在开孔处犹如产生一道“气墙”，因而开孔对模型周围空气流场的破坏程度不大.此时对于建筑外部而言，相当于没有开孔，故孔口处的风压等于没有开孔时的外部风压，则平均内压也等于没有开孔时的孔口处外压.

2 多洞口模型的数值模拟

以上讨论的是开单一主洞口情况下风致内压问题，而实际情况下强风导致的结构围护结构破坏是难以预料的，有可能出现多处破坏的情况 .下面研究0°风向角时迎风纵墙A与背风屋面B（背风纵墙B）同时开洞情况下的风致内压问题，主要考察多洞口情况下外风压变化情况，以及风致内压随洞口面积比（β）变化的规律 .其中：β为迎风纵墙A的开洞面积AW与背风面的开洞面积AL的比.图2为多洞口位置与风向角示意图，其网格划分、边界条件及参数设置均与节1.2相同.

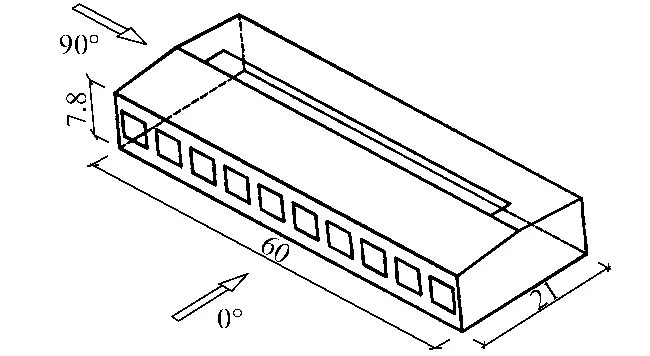
图2 多洞口模型与风向角示意图Fig.2 Multi－opening model and wind attack angle

2.1 迎风纵墙与屋面同时开洞的模拟

基本模型与节1.1相同，纵墙A上洞口尺寸为4m×3.5m；屋面B上洞口尺寸为20m×2.5m时，对应纵墙A上洞口数量分别取1，2，4，8，10个；屋面B上洞口尺寸为10m×2.5m时，对应纵墙A上洞口数量取6，10个，由此共得到7种组合工况.7种组合工况对应的洞口面积比（β）分别为0.28，0.56，1.12，2.24，2.80，3.36和5.60.

7种工况多洞口模型结构表面平均风压系数的数值模拟，如表3所示.表3中：C¯P，E为平均外风压系数；C¯P，I为平均内风压系数.由表3可知：不同开洞面积比对结构表面平均外风压系数的影响很小，可以认为在流动稳态阶段结构内部风场对外部风场的影响较小.

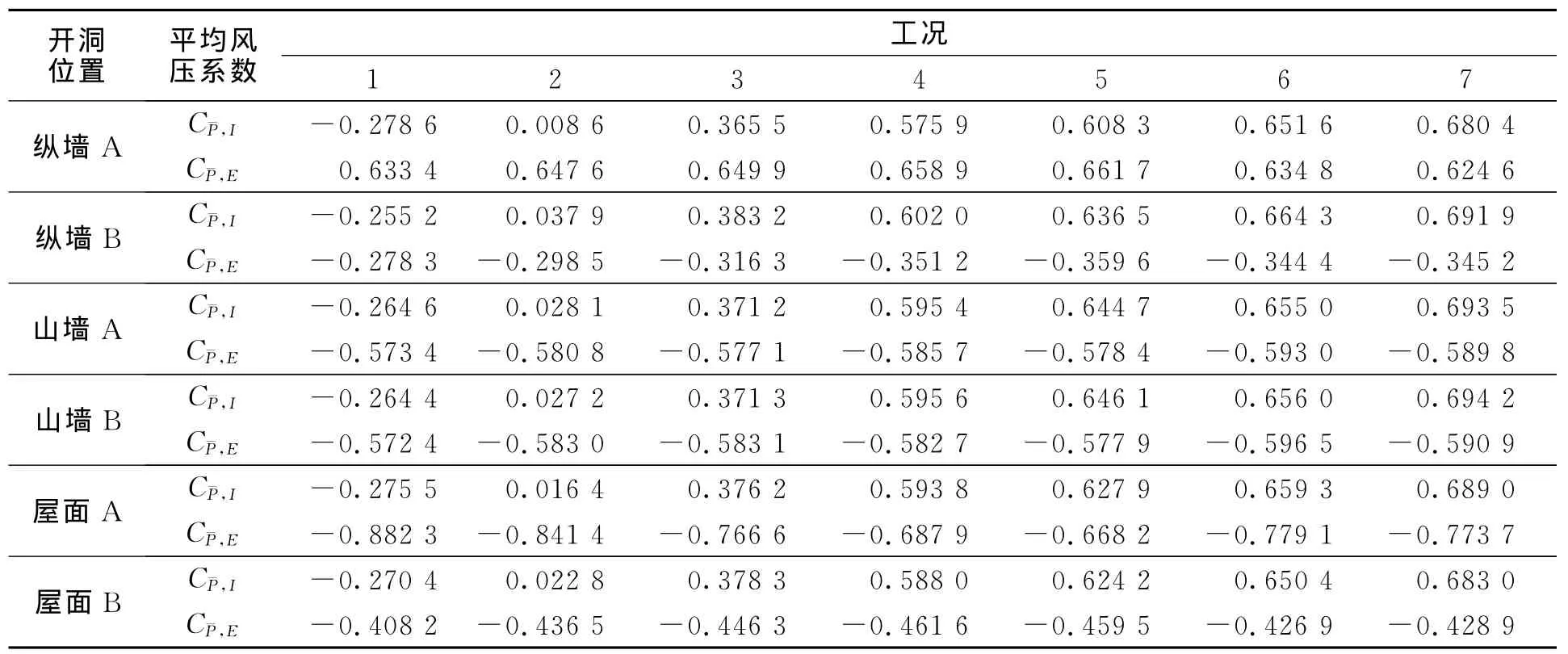
表3 各工况多洞口模型结构表面平均风压系数Tab.3 Mean internal and external pressure coefficients of multi－opening models

当开洞面积比β一定时，结构各表面内压系数分布均匀，可以用一个平均值来表示结构各面的平均内风压系数.在迎风纵墙与屋面同时开洞时，7种工况的结构表面内压系数随开洞面积比β变化的模拟结果与理论计算结果的比较，如图3所示.

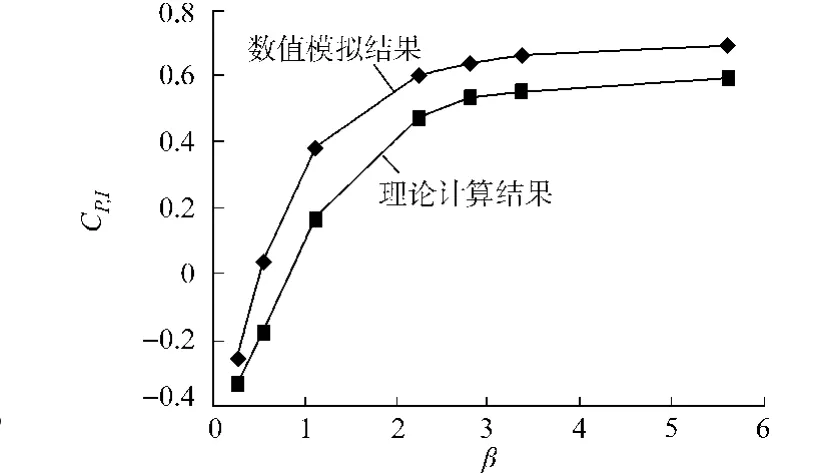
图3 迎风纵墙与屋面同时开洞的模拟与计算结果比较Fig.3 Simulation results for the openings on both windward wall and roof

2.2 迎风纵墙与背风纵墙同时开洞的模拟

基本模型仍与节1.1相同，迎风纵墙A和背风纵墙B上洞口尺寸均为4m×3.5m，各墙面洞口数量及其组合见表4，由此共得到6种组合工况，洞口面积比β分别为0.2，0.4，1.0，2.5，4.0，8.0.其网格划分、边界条件及其他参数设置均与节1.2相同.

由数值模拟结果可知，迎风纵墙与背风纵墙同时开洞情况下，建筑内部流场受开洞位置的影响较大；内压分布的不均匀性比单一主洞口时显著增强，尤其是背风纵墙和背风屋面的内风压受流场影响较大.为考虑内压随洞口面积比的变化情况，仍以单位面积的风压系数加权平均值来表示内风压系数 .在迎风纵墙与背风纵墙同时开洞时，其平均内压系数随β变化的数值模拟与理论计算结果比较，如图4所示.图5为不同β时各面平均外压系数变化情况.

由以上分析结果可得多洞口情况的几点结论：1）0°风向角时，迎风面与背风面同时开洞工况下，风致外压不随洞口面积比β的改变而变化，说明在流动稳态阶段洞口处空气流动达到平衡状态，结构内部风场对外部风场的影响较小；2）平均内风压系数随着洞口面积比的增大而增大，但增大趋势逐渐变缓，当洞口面积比大于3后趋于常值，且数值模拟结果与由文献［4］推导的理论计算公式计算结果趋势完全吻合，但仍存在一定误差.

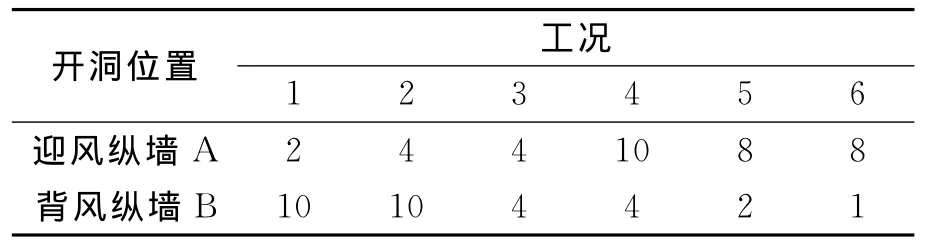
表4 迎风纵墙与背风纵墙开洞组合Tab.4 Opening combination of windward wall and leeward wall

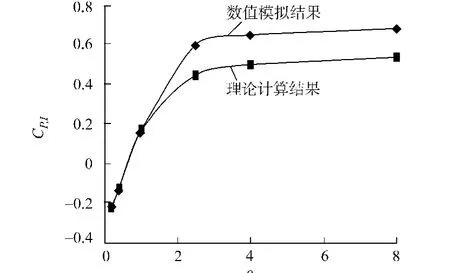
图4 迎风纵墙与背风纵墙同时开洞的模拟与计算结果比较Fig.4 Simulation results for the openings on both windward wall and leeward wall

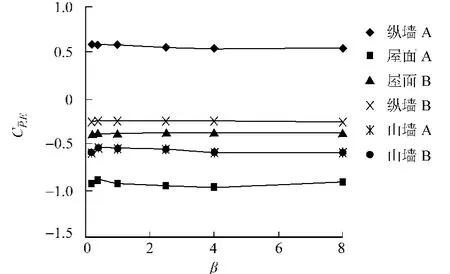
图5 各表面外压系数随洞口 面积比的变化情况Fig.5 Variation of External pressure coefficients to different opening ratios

3 不同风向角工况的数值模拟

3.1 模型描述

以上所讨论的均是0°风向角下结构表面内压分布情况，下面以节2.1的工况7模型为基础讨论风向角对内压分布的影响.图2为其风向角的定义，顺时针为正，风向角的变化从0°到90°，间隔为15°，共7种工况.由前述可知，当洞口面积比大于3，其平均内压系数趋于常值，本节所讨论模型洞口面积比β为5.6.由于随着风向角的变化，图2结构各表面不再严格符合迎风面或背风面的定义，洞口面积比β是变量，本节定义β是纵墙A与屋面B的洞口面积比，其他边界条件及参数的设定参照节1.2.

3.2 数值模拟结果分析

不同风向角下，结构内表面平均风压系数及其标准差，如图6所示.由图6可以看出：随着风向角的增大，平均内压系数呈减小趋势，同时内压分布的不均匀性显著增强.这是由于在斜风向作用下，结构外表面风压分布十分不均匀，当结构表面有多处洞口时，气流从外风压大的洞口处流入，从外风压相对小一些的洞口流出，结构内部靠近洞口处和转角的地方多处均有漩涡产生，也就导致了内压分布的不均匀.

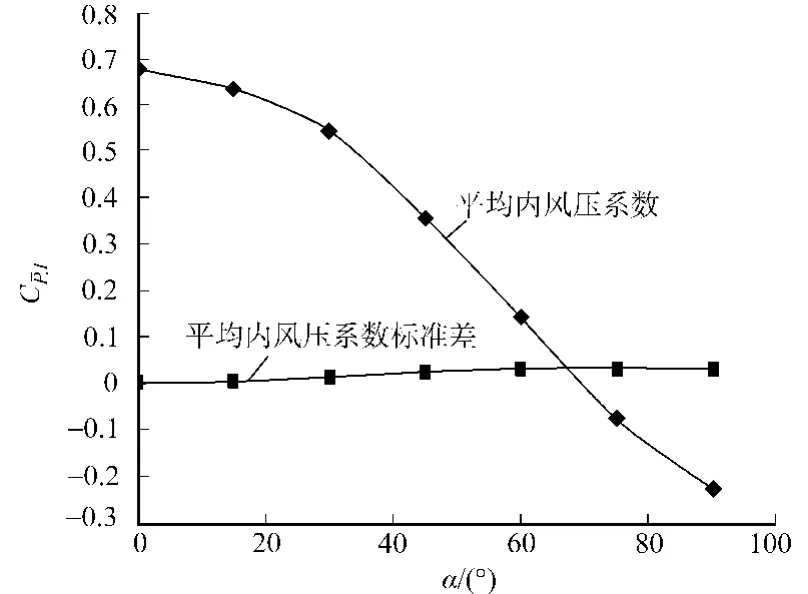
图6 不同风向角下平均内风压系数和内风压系数标准差Fig.6 Mean internal pressure coefficients and standard deviation at different wind attack angles

屋面净风压系数随风向角变化的情况，如图7所示.由图7可以看出：0°风向角下屋面平均净风压系数取最大值，相比封闭结构屋面净压增大约1.6倍.所述模型与文献［15］纵墙和山墙同时开洞模型得到相同的结论.

4 结论

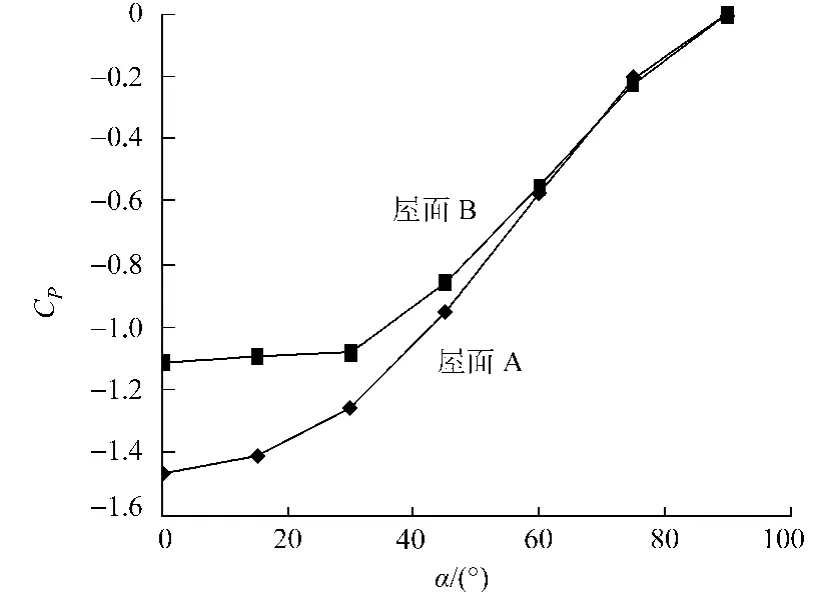
图7 不同风向角下屋面净风压系数Fig.7 Net pressure coefficients at different wind attack angle

采用数值风洞对单一主洞口及多洞口低矮建筑模型进行稳态流动阶段风致内压分布规律的分析，得到以下3点主要结论.

1）结构表面出现单一主洞口情况下，开孔率对内压几乎没有影响，但开洞位置的不同对平均内风压的分布影响显著.

2）结构表面有多个洞口情况下，0°风向角时，开洞位置对结构内部风场影响较大，但对外部风场几乎没有影响；不同开洞面积比对结构表面平均外风压的影响很小，而平均内风压随着洞口面积比的增大而增大，但增大趋势逐渐变缓，当洞口面积比大于3时，平均内风压趋于常值.

3）在结构纵墙和屋面同时开洞且开洞面积比一定时，结构平均内风压系数随风向角变化显著，且内压分布的不均匀性显著增强，0°风向角下屋面平均净风压系数取得最大值.

结论可为强风地区低矮房屋结构设计提供参考，同时建议我国现行国家标准GB 50009－2001《建筑结构荷载规范》［23］在强风多发地区应考虑风致内压问题.开孔结构风致内压对建筑结构作用的研究是结构风工程领域的新课题，文中只就开孔结构风荷载进行了稳态阶段的数值模拟研究，并未涉及脉动风的影响.事实上，仅仅模拟湍流的稳态阶段对于开孔结构风致内压的研究是不够的，脉动风荷载和突然开孔时引起的瞬时脉冲效应的研究、结构风致振动及流固耦合效应的研究是风致内压研究领域的热点和难点，也是需深入开展工作.

［1］SHANMUGASUNDARAM J，ARUNACHALAM S，GOMATHINAYAGAM S，et al.Cyclone damage to buildings and structures：A case study［J］.Journal of Wind Engineering and Industrial Aerodynamics，2000，84（3）：369－380.

［2］台州市建设规划局.0414号台风“云娜”台州民房倒塌调查报告［R］.台州：台州市建设规划局，2004.

［3］赵雅丽，全涌，黄鹏，等.典型双坡屋面风压分布特性风洞试验研究［J］.同济大学学报：自然科学版，2010，38（11）：1588－1592.

［4］LIU H.Building code requirements on internal pressure［C］∥Proc 3rd U.S.National Conference of Wind Engineering Research.Florida：International Association for Wind Engineering，1978：1－7.

［5］VICKERY B J，BLOXHAM C.Internal pressure dynamics with a dominant opening［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，41／42／43／44：193－204.

［6］STATHOPOULOS T，LUCHIAN H D.Transient wind induced internal pressures［J］.Journal of the Engineering Mechanics Division，1989，115（7）：1501－1514.

［7］HOLMES J D.Mean and fluctuating internal pressures by wind［C］∥Proc 5th International Conference on Wind Engineering.Oxford：Pergamon Press，1997：435－450.

［8］WOODS A R，BLACKMORE P A.The effect of dominant openings and porosity on internal pressures［J］.Journal of Wind Engineering and Industrial Aerodynamics，1995，57（2／3）：167－177.

［9］BESET F，CERMAK J E.Correlation of internal and area－averages external wind pressures on low－rise buildings［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，69／70／71：557－566.

［10］SHARMA R N，RICHARDS P J.The influence of Helmholtz resonance on internal pressures in a low－rise building［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91（6）：807－828.

［11］SHARMA R N.Internal and net envelop pressures in a building having quasi－static flexibility and a dominant opening［J］.Journal of Wind Engineering and Industrial Aerodynamics，2008，96（6／7）：1074－1083.

［12］余世策，楼文娟，孙炳楠，等.背景孔隙对开孔结构风致内压响应的影响［J］.土木工程学报，2006，39（6）：6－11.

［13］楼文娟，卢旦，孙炳楠 .风致内压及其对屋盖结构的作用研究现状评述［J］.建筑科学与工程学报，2005，22（1）：76－82.

［14］卢旦，楼文娟，唐锦春.开孔结构风致内压研究［J］.浙江大学学报：工学版，2005，39（9）：1388－1392.

［15］宋芳芳，欧进萍.低矮建筑风致内压数值模拟与分析［J］.建筑结构学报，2010，31（4）：69－77.

［16］LEVITAN M L，MEHTA K C，VANN W P.Field measurements of pressure on the texas tech building［J］.Journal of Wind Engineering and Industrial Aerodynamics，1991，38（2／3）：227－234.

［17］LEVITAN M L，MEHTA K C.Texas tech field experiments for wind loads partⅠ：Building and pressure measuring system［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，41／42／43／44：1565－1576.

［18］LEVITAN M L，MEHTA K C.Texas tech field experiments for wind loads partⅡ：Meteorological instrumentation and terrain parameters［J］.Journal of Wind Engineering and Industrial Aerodynamics，1992，41／42／43／44：1577－1588.

［19］黄本才.结构抗风分析原理及应用［M］.上海：同济大学出版社，2001.

［20］周绪红，聂少锋，周天华，等.低层双坡屋面建筑三维定常风场的数值模拟［J］.工程力学，2010，27（3）：19－29.

［21］殷惠君，张其林，周志勇.标准低矮建筑 TTU 三维定常风场数值模拟研究［J］.工程力学，2007，24（2）：139－145.

［22］Architectural Institute of Japan.AIJ recommendations for loads on buildings［S］.Tokyo：AIJ，1996.

［23］中华人民共和国建设部.GB 50009－2001建筑结构荷载规范［S］.北京：中国建筑工业出版社，2002.

Numerical Simulation of Wind－Induced Internal Pressure on Gable Roof Low－Rise Buildings

XIAO Ming－kui1，2，ZHAO Min1，WANG Tao1

（1.College of Civil Engineering，Chongqing University，Chongqing 400045，China；2.Key Laboratory of New Technology for Construction of Cities in Mountain Area，Chongqing University，Chongqing 400045，China）

The main damages of buildings in gale occurred by the combined effect of external pressure and wind－induced internal pressure which is caused by the sudden openings on structure surfaces.A standard k－εmodel，the Reynolds Averaged Navier－Stokes Equations（RANS）turbulence model，was adopted to numerically simulate different cases of low－rise buildings with one main opening or multi－openings with fluid dynamics software ANSYS Fluent 12.0.The analysis results show that，for single dominant opening cases，the opening ratios doesn′t affect the wind－induced internal pressure，while the opening′locations affect both the magnitude and distribution of wind－induced internal pressures；for multi－openings cases at 0°wind attack angle，the mean internal pressure coefficients increase with increasing the opening ratio，but the trend of increase gradually slows down；at a certain ratio of AW／AL，the mean internal pressure is affected significantly by the wind attack angle，and the inhomogeneity of internal pressure enhances markedly.

computational fluid dynamics；gable roof；wind－induced internal pressure；numerical simulation；turbulence model

TU 312.1

A

1000－5013（2012）03－0310－07

2011－11－27

肖明葵（1952－），女，教授，主要从事工程力学与工程结构抗震动力分析的研究.E－mail：xmkxy＠yahoo.com.cn.

教育部科学技术研究重点项目（108175）；重庆市自然科学基金资助项目（2007BB0126）

（责任编辑：黄晓楠 英文审校：方德平）