课堂教学评估的多层次贝叶斯网络分类器方法

李兰春，王双成，王 辉

（1.上海立信会计学院外语学院，上海 201620；2.上海立信会计学院数学与信息学院，上海 201620；3.中央民族大学信息工程学院，北京 100081）

课堂教学评估的多层次贝叶斯网络分类器方法

李兰春1，王双成2，王 辉3

（1.上海立信会计学院外语学院，上海 201620；2.上海立信会计学院数学与信息学院，上海 201620；3.中央民族大学信息工程学院，北京 100081）

课堂教学是为实现一定的教学目标而展开的信息传递、过程控制和策略实施过程.依据课堂教学的特点给出了课堂教学评估的指标体系，并在此基础上建立了课堂教学评估的层次贝叶斯网络分类器模型.为提高分类器的分类识别准确率，在连续属性中引入形状参数，实验结果显示，通过形状参数的优化能够显著提高分类器的分类识别可靠性.

课堂教学；朴素贝叶斯网络；分类器；评估

0 引言

课堂教学是为实现一定的教学目标，通过信息传递、过程控制和策略实施而展开的师生之间的双边活动.［1－2］课堂教学已经具有悠久的历史，在相当长的一段时间内仍将是一种主要的教学方式，也是学生建立知识结构、发展认知结构和人格形成的主要途径.课堂教学质量评估能够为制定更科学的教学策略提供具有针对性的信息，有助于推动教学改革和提高教学质量.目前课堂教学评估主要采用三级指标体系［3－4］，在指标之间具有线性关系的假设下，根据三级指标计算出二级指标，再由二级指标最终确定一级指标的等级.这一等级判断过程是一个层次分类问题（模拟人类概念学习与应用的技术），而且基于分类器的课堂教学质量等级判断不需要线性关系的假设，因此在评价的可靠性方面具有优势，并可开拓课堂教学评估的新思路.

现在已经有了许多著名的分类器，如神经网络、支持向量机、决策树、统计判别分析和贝叶斯网络等，它们在许多领域得到了广泛的应用.但这些分类器往往都需要许多例子数据进行学习.课堂教学方面的例子数据一般比较少，而且其中的连续数据也不适合于离散化（离散化会丢失过多的信息）.朴素贝叶斯网络（naive Bayesian network，简记为NBN）［5－6］分类器是目前最适合于小例子集分类预测的概率分类器，这种分类器不需要许多例子数据用于训练，并且能够直接处理连续属性.在朴素贝叶斯网络分类器中处理连续属性的核心问题是条件密度估计，目前主要采用两种方式来估计条件密度［7－8］：一种是使用高斯函数来估计属性条件密度，而高斯函数可能与实际密度函数有较大的差距，从而影响分类器的分类准确性；另一种是采用高斯核函数估计属性条件密度，高斯核函数又易于导致对例子的过度拟合，也同样会降低分类器的泛化能力.

本文从课堂教学的信息传递、过程控制和教学策略三个方面来制定课堂教学质量评估的指标体系，并针对课堂教学质量评估的实际情况和需求建立多层次朴素贝叶斯网络（mult－hierarchical naive Bayesian network，简记为MHNBN）分类器模型.为避免使用高斯核函数估计属性条件密度可能导致的对例子过度拟合问题，在高斯核函数中引入形状参数，并通过形状参数的优化来提高分类器的分类识别准确性.

1 MHNBN分类器学习

MHNBN分类器学习包括结构学习和参数学习两部分.结构学习一般是依据专家的领域知识确定指标之间的层次关系；参数学习是使用例子数据进行边缘和条件概率估计，以及在某种分布假设下的连续属性条件密度估计.

1.1 MHNBN分类器结构

NBN分类器基于这样的假设：当类变量给定时，属性变量之间条件独立.这一假设决定了NBN分类器结构是星形结构.MHNBN分类器是NBN分类器的层次组合，下面给出标准NBN分类器结构（用S表示）和一个三层次MHNBN分类器的层次树，如图1所示.

图1 NBN分类器结构和分类器层次树

在图1（a）的标准NBN分类器结构中，类结点是所有属性结点的唯一父结点；图1（b）是将NBN分类器作为一个结点而得到的MHNBN分类器层次结构树，将图1（b）的上面两层展开后的分类器结构如图2所示.

图2 展开后的两层次分类器结构

1.2 MHNBN分类器参数学习

MHNBN分类器参数学习是依据例子数据估计概率和密度的过程，以图2所示的两层次分类器（分别称为上层分类器和下层分类器）为例给出参数学习方法.在由一级和二级指标构成的上层分类器中，C和X u1，…，X ut都是离散指标变量；而由二级和三级指标构成的下层分类器中，底层指标X u11，…，X u1v1，X u21，…，X u2v2，…，X ut1，…，X utvt可以是离散或连续指标.

1.2.1 一级和二级指标边缘概率估计

采用最大似然估计方法，那么，一级和二级指标需要估计边缘概率（先验概率）.

一级指标边缘概率估计：

其中N（c｜D）为例子数据集D中第c类（C＝c）的例子数量，N（D）为所有例子数量.

二级指标边缘概率估计：

其中N（x ui｜D）为例子数据集D中第x ui类（X ui＝x ui）的例子数量.

1.2.2 二级和三级指标条件概率或密度估计

对于非叶子结点的二级或三级指标，只需要估计条件概率；而对作为叶子结点的二级或三级指标可能要估计条件概率（离散指标）和条件密度（连续指标）.

二级离散指标的条件概率估计：

其中N（x ui，c｜D）为第c类中X ui＝x ui的例子数量.

三级离散指标的条件概率估计：

其中N（x ui k，x ui｜D）为第x ui类中X uik＝x uik的例子数量.

三级连续指标的条件密度估计：

2 MHNBN分类器表示形式与分类过程

以两个层次的MHNBN分类器为例，给出MHNBN分类器的表示形式和分类过程.基于贝叶斯网络理论和贝叶斯公式，以及图2中所体现的条件独立性关系，可得：

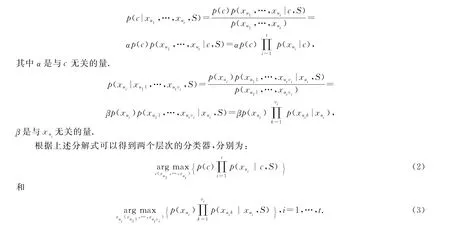
分类过程是：首先由下层分类器确定二级指标X u1，…，X ut的值，然后再基于上层分类器得到一级指标的值.多层次分类器的分类也是这样的自下而上的过程.

3 课堂教学评估

首先建立课堂教学评估指标体系，然后结合指标体系与例子数据便能够建立MHNBN分类器，并基于MHNBN分类器进行课堂教学评估.

3.1 课堂教学评估指标体系

指标体系是进行课堂教学评估的前提，依据教育控制论、系统科学原理和课堂教学机制等建立一个课堂教学评估三级指标体系，也可根据实际需要对指标体系进行层次扩展.

（1）一级指标

课堂教学等级（C）分4个级别，分别是：A级（优秀），B级（良好），C级（一般），D级（较差）.

（2）二级指标

课堂教学所属的二级指标是：课堂信息传递（X1），课堂教学控制（X2），课堂教学策略（X3）.它们都分三个等级，分别是A级（好），B级（中）和C级（差）

（3）三级指标

课堂信息传递所属的三级指标：教师向学生的信息传递（语法信息传递（X11），语义信息传递（X12），语用信息传递（X13）），学生向教师的信息传递（反馈信息（X14），前馈信息（X15），退馈信息（X16））.

课堂教学控制所属的三级指标：知识结构控制（概念（X21），规则（X22），问题解决（X23）），认知结构控制（认知操作（X24），动力供给（X25），认知策略（X26）），方式控制（程序控制（X27），随机控制（X28））.

课堂教学策略所属的三级指标：讲授式教学（X31），启发式教学（X32），演绎式教学（X33），概括式教学（X34），回溯式教学（X35）.

3.2 课堂教学评估的分类器模型

根据上面的课堂教学评估指标体系可得到两层次的MHNBN分类器结构，如图3所示.

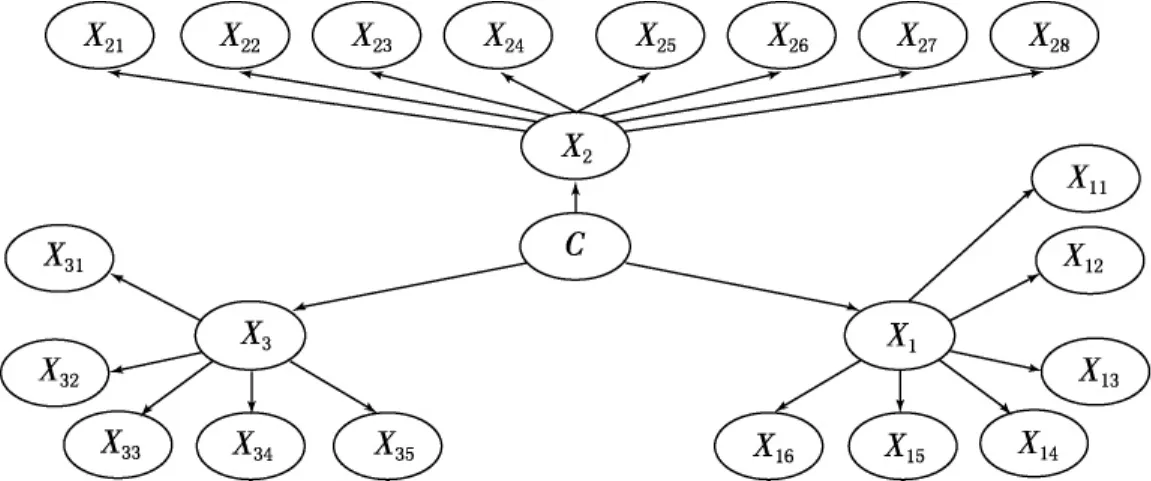
图3 用于课堂教学评估的MHNBN分类器结构

基于分类器结构和例子数据进行参数估计，从而得到用于课堂教学评估的MHNBN分类器，输入最新课堂教学信息，通过分类运算便可获得课堂教学的等级.

3.3 NBN分类器可靠性实验与分析

在UCI机器学习数据仓库［9］中选择12个具有连续属性的分类数据集，分别使用对连续属性离散化（DNBN）、高斯密度估计（GNBN）、高斯核密度估计（GKNBN）和引入形状数的高斯核密度估计（GKSNBN）而得到的NBN分类器进行分类预测，采用10折交叉有效性（10－fold cross－validation）验证方法进行分类器的分类准确性估计，如表1所示.

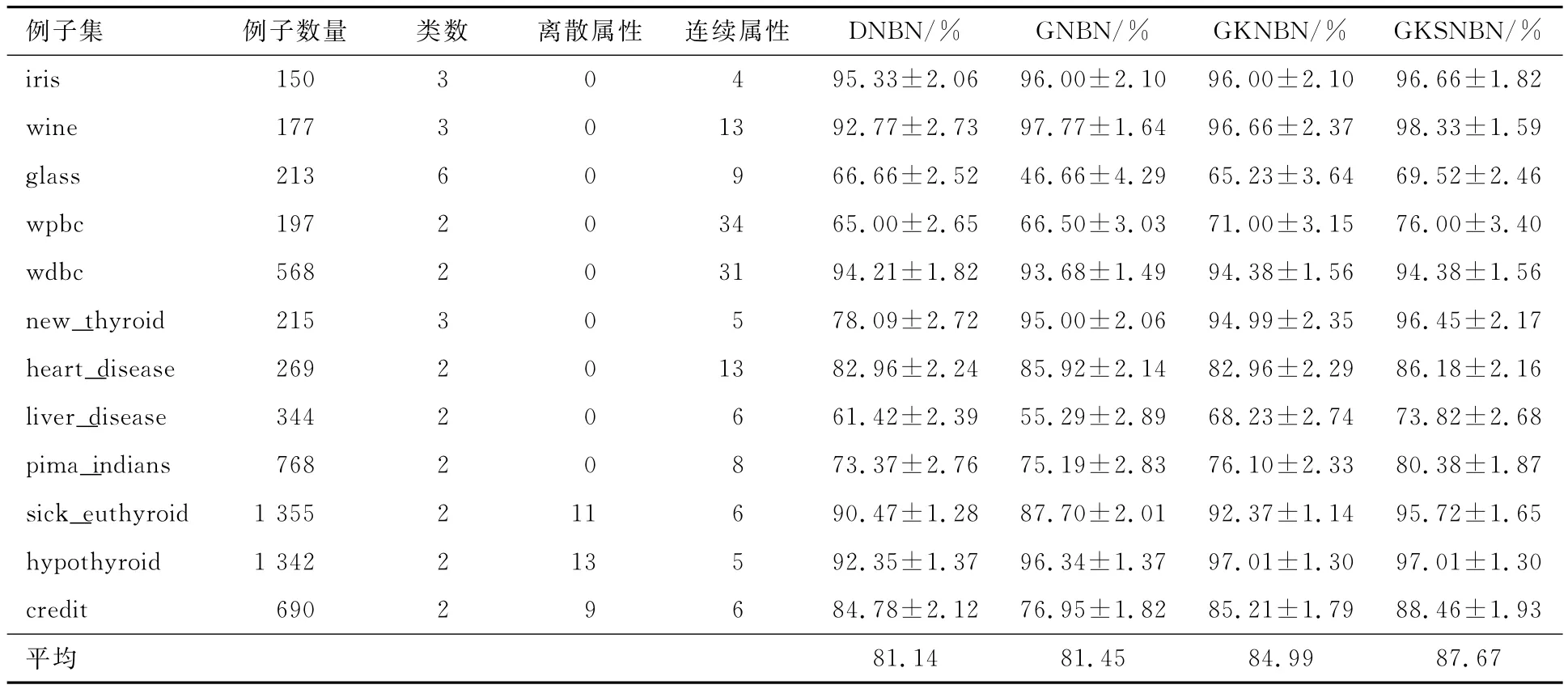
表1 分类预测准确率比较

从表1中可以看出，DNBN分类器具有良好的分类准确率，而GKNBN分类器要优于DNBN和GNBN分类器，GKSNBN分类器还要优于GKNBN分类器.这表明使用把DNBN分类器和GKSNBN分类器层次组合而得到的MHNBN分类器，进行课堂教学评估等级判断将是比较可靠的.

4 小结

根据教育控制论、系统科学原理和课堂教学机制等给出了一个课堂教学评估的三级指标体系，在此基础上，具有针对性地建立了用于课堂教学评估的动态层次朴素贝叶斯网络分类器.为提高分类器层次组件的分类准确性，在连续属性的条件密度估计中引入了形状参数，并通过形状参数的优化来提高分类器的泛化能力，实验结果显示，形状参数的优化能够显著提高分类器的分类准确性，这表明将其用于课堂教学质量评估，所得到的评估识别结果会更加可靠.

［1］王黎.应用型本科经济学课堂教学改革探索［J］.教育探索，2010，1：64－65

［2］杨金观，聂建峰.课堂教学质量评价——一个在高校实际工作中被误解的概念［J］.高教发展与评估，2010，1：15－20.

［3］陈弘，李幽铮，郑钢.基于AHP法的教师教学质量评估改进模型［J］.金陵科技学院学报，2010，26（1）：31－34.

［4］刘香芹，陈侠.模糊多层次多属性高校教师教学质量评估［J］.沈阳航空工业学院学报，2010，27（2）：90－92.

［5］RAMONI M，SEBASTIANI P.Robust Bayes classifiers［J］.Artificial Intelligence，2001，125（1／2）：209－226.

［6］JING Y S，PAVLOVI C＇V，REHG J M.Boosted Bayesian network classifiers［J］.Machine Learning，2008，73（2）：155－184.

［7］JOHN G H，LANGLEY P.Estimating continuous distributions in Bayesian classifiers.［C］／／Proceedings of the 11th International Conference on Uncertainty in Artificial Intelligence，Bec Canada：Qu ＆Eacute，1995：106－143.

［8］PÉREZ A，LARRANAGA P，INZA I.Bayesian classifiers based on kernel density estimation［J］.International Journal of Approximate Reasoning：Flexible Classifiers，2009，50（2）：341－362.

［9］MURPHY S L，AHA D W.UCI repository of machine learning databases［EB／OR］.［2009－12－04］.http：／／www.ics.uci.edu／～mlearn／MLRepository.Html.

The method of mult－hierarchical Bayesian network classifier for classroom teaching assessment

LI Lan－chun1，WANG Shuang－cheng2，WANG Hui3

（1.School of Foreign Studies，Shanghai Lixin University of Commerce，Shanghai 201620，China；2.School of Mathematics and Information，Shanghai Lixin University of Commerce，Shanghai 201620，China；3.School of Information Engineering，The Central University for Nationalities，Beijing 100081，China）

The classroom teaching is a process of teaching information transfer，classroom control and implementation of teaching strategies for realizing certain educational objectives.A index system of classroom teaching assessment is presented based on the features of classroom teaching.And a model of mult－hierarchical naive Bayesian network classifier is developed for classroom teaching assessment.In order to improve the classification accuracy of classifier，the shape parameter is pulled in continuous attributes.Experimental results show that the reliability of classifier can be significantly improved by shape parameter optimization.

classroom teaching；naive Bayesian network；classifier；assessment

TP 181

520·20

A

1000－1832（2012）01－0050－05

2011－02－04

国家自然科学基金资助项目（60675036）；教育部人文社科基金资助项目（10YJA630154）；上海市教委重点学科建设项

目（J51702）；上海市教委科研创新重点项目（09zz202）.

李兰春（1959—），女，讲师，主要从事教育原理与评估研究；王双成（1958—），男，博士，教授，主要从事智能数据处理研究；王辉（1961—），男，硕士，教授，主要从事决策支持技术研究.

陶 理）