随机抽样中的Alias算法及其改进

贾文宝，王仲奇，张本爱

（1.南京航空航天大学，江苏 南京 210016；

2.中国原子能科学研究院，北京 102413；

3.北京应用物理与计算数学研究所，北京 100088）

随机抽样中的Alias算法及其改进

贾文宝1，王仲奇2，张本爱3

（1.南京航空航天大学，江苏 南京 210016；

2.中国原子能科学研究院，北京 102413；

3.北京应用物理与计算数学研究所，北京 100088）

为减少随机数的使用次数和降低抽样时间，基于等概化思路（或古典概型思路），对著名的Alias抽样方法进行了改进.以存储空间的少量增加为代价，使改进后的抽样方法A＿Ⅰ和A＿Ⅱ随机数的平均使用次数为Alias方法的75%和62.5%，平均抽样时间大约为Alias方法的80%和70%.

Alias方法；改进；随机抽样

随机变量抽样是蒙特卡罗方法的基础，同时也在其他许多领域广泛使用.由于计算机的特征与限制，通常连续型随机变量也要化作离散型随机变量来处理，因此离散型随机变量的抽样方法是概率统计学科中的一个重要问题.为了方便起见，除特殊指明外，我们提到的随机变量均为离散型随机变量.

同时为了论述方便，首先将任意离散型随机变量不失一般性地转换成为

式中P1，P2，…为相应的概率.

直接抽样方法也称查找算法，完全基于离散随机变量概率分布的定义而得到的.它的抽样思路十分简洁，被称为“非常理想”的方法［1］.它是通过将随机数与阶梯性的随机变量分布值逐项比较而确定相应的随机事件.为了得到所需要的随机事件，直接抽样方法所需进行的比较次数同样也形成了另外一个随机变量，而这个随机变量的数学期望与原随机变量的数学期望是一致的.这就形成2个问题：不确定的比较次数提高了抽样算法实现的复杂程度，影响了计算机的编译系统对程序的优化程度，这在并行化处理中颇受关注；对于数学期望比较大的随机变量来说，不断的比较将增加抽样所需时间.

A.J.Walker在1974年给出了一个很巧妙的算法——Alias算法［2－4］，大大改善了对随机变量的抽样方法.在Alias算法中，只需要使用2个随机数，进行一次与随机数的比较操作，即可得到随机变量的样本.

我们将讨论Alias算法，并以此为基础进行改进，减少对随机数的使用，减少抽样所需的时间.

1 直接抽样方法

对于随机变量（1）有直接抽样方法

很明显，对于任意的离散型分布，都可以利用（2）式实现其抽样.因此，从这个角度上说，直接抽样是一个简单而理想的算法.

由于在计算机处理中，进行一次比较操作所需时间将超过进行四则运算操作所需时间，而且比较操作将影响计算机处理的流程，妨碍编译系统对程序的优化，也就是说，在计算机上“比较”操作是一个“不好”的操作，应该尽量避免和减少.因此所需比较的次数是抽样方法优劣的一个标志，应想办法减少所需比较的次数.

由（2）式可知，要确定对应于随机数ξ的样本值XF，需要通过将ξ与F（xi）不断的比较而得到.对于一个确定的离散型分布，抽样所需要进行的比较次数的数学期望应为

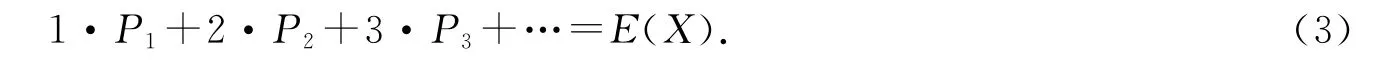
总的来说，抽样所需比较次数首先取决于随机变量的容量，即包含的随机事件的数量.随机事件越多所需比较的次数就越多；其次随机事件的排列秩序的不同也将影响抽样所需比较次数的不同，概率大的事件秩序越靠前，所需比较的次数越少，反之亦然.例如下面一个随机变量的不同表述方法所需抽样比较的次数就会不同：

计算将显示，利用（2）式抽样，基于X1表述的随机变量所需的比较次数将大于基于X2的比较次数.

这说明随机变量表述方法对抽样所需比较次数存在影响，但这个影响是可以很简单去掉的.而随机变量容量对比较次数的影响则是本质.如何减少抽样所需比较的次数，是改进抽样方法的目标.

2 Alias算法

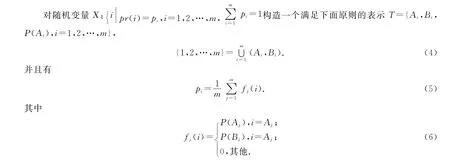
随机变量X：｛Pi＝1／M，i＝1，2，…，M｝，这是一个事件等概率的随机变量.对它的抽样是非常简单的XF＝i，如果［M·ξ］＋1＝i.这里不需要任何比较操作.这是因为随机变量所包含的随机事件具有等概率的独特性质.如果将随机事件进行“等概化变形”就可能会减少比较次数的途径.

对i＝1，2，…，m.基于这个表示，以1／m的等概率确定表中的一个单元（AI，BI，P（Ai）），再利用一个随机数用直接抽样确定AI或BI，进而确定XF.文献［5-6］分别给出了相应的证明.

可以将Alias算法的流程表述如下［7］.持续执行上述过程直至所有的事件都完全归入表中，再将所有的P（Ai）乘上相同的倍数m即可.

第二步：抽样

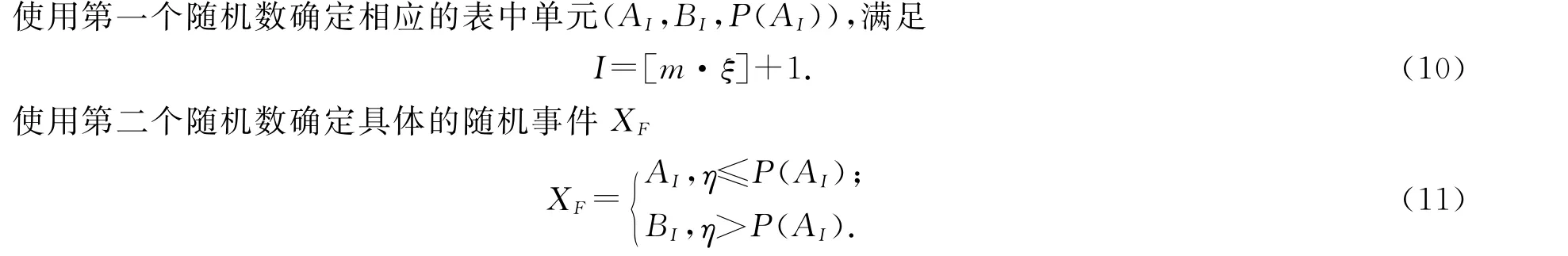
由此可以看出无论多大容量的随机变量，使用Alias算法抽样都只需进行1次与随机数的比较，这样将大大的节省抽样所需时间，这将从后面的计算中体现出来.但是在减少比较操作次数的同时，Alias算法比直接抽样方法多使用了一个随机数.

3 对Alias算法的改进

Alias算法的思路是将随机变量进行适当变形向等概率方向靠近.沿着这个思路，继续尝试对Alias算法进行再次变形，以考察其是否能够进一步减少判断比较的次数或减少随机数的使用次数.

基于表T构造新的 Alias表：T′＝｛A′i，B′i，P（A′i），i＝1，2，…，2m｝，即将每一个单元（Ai，Bi，P（Ai））变为2个单元

这样我们将随机变量变形为等概率的2部分组成，各由等概率单元组成.其中一部分的单元由概率为1的单“子事件”构成（原随机事件可以包含多个“子事件”）；而另一部分的单元由2个不等概率的“子事件”组成.

使用Alias抽样方法，当确定的单元为单“子事件”单元则必然事件发生，不必继续判断；当确定的单元为双“子事件”单元，与Alias算法做相同的工作.我们称上面Alias算法的变化为1次改进.

同理，以构造对Alias算法的1改进（为方便起见，将Alias方法记做A方法，将对Alias方法的1改进记做A＿Ⅰ方法，将对Alias方法的2改进记做A＿Ⅱ方法）.这样随机变量就变形为由等概率的4部分组成，其中3部分的单元均为单“子事件”单元，只有1部分的单元为双“子事件”单元.

4 计算分析

为了直观的比较Alias算法以及其改进算法与直接抽样方法，随机地构造随机变量，计算上述各种方法在对已确定的随机变量抽样时产生的误差和花费的计算机时间.

首先均匀随机产生各个事件的概率，作为待抽样随机变量.对于这个随机变量分别用直接抽样方法（DI），Alias抽样方法（Alias）以及关于Alias方法的1改进（A＿Ⅰ）与2改进方法（A＿Ⅱ）进行抽样，考察它们所形成的抽样误差和所耗费的计算机时间.

计算结果显示，这几种方法所形成的抽样误差是相当的.而在计算机时间上则随着随机变量容量的增大体现出明显的区别.

图1给出对于不同容量的随机变量，各种抽样方法所需抽样时间.从图1可以看出，当随机变量容量比较小时，Alias系列方法并不比直接抽样方法优越；当容量比较大时，Alias系列抽样方法体现出其优势所在.Alias系列抽样方法的抽样时间在随机变量容量变化时保持稳定，不随容量的增大而增大，而直接抽样的抽样时间与随机变量的容量是相关的.

前面提到，对于不同的随机事件排列次序的相同容量的随机变量，直接抽样方法的比较次数并不相同，因此其抽样时间也是不相同的.图2给出了容量为40的不同随机变量的抽样时间的分布情况.图2中所显示的是不同抽样方法对于所含随机事件容量相同但排列次序不同的随机变量的抽样时间，出于方便的考虑直接抽样所需的比较次数来放映随机事件的不同排列.这个结果反映了Alias系列方法的抽样时间既不随随机变量的容量变化而变化，也基本上不随随机事件排列次序的变化而变化.

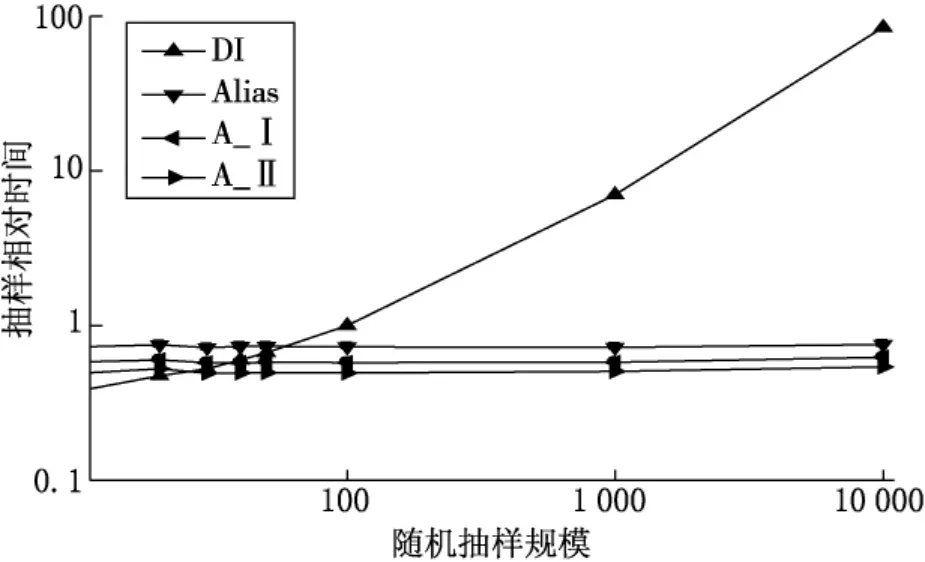
图1 不同抽样方法的随机变量的容量与抽样时间的变化趋势

Alias系列方法的这个特点是非常重要的.在研究容量巨大的随机变量的抽样和考虑抽样的并行化问题时，充分利用Alias系列方法，将非常有利于问题的解决.

在Alias抽样中需要使用2个随机数，进行1次比较.在Alias的1次改进抽样中，对于一半的情况只需使用1个随机数，不需要进行比较；而对另一半情况需要使用2个随机数进行1次比较.在Alias的2次改进抽样中，对1和4情况需要使用2个随机数，进行1次比较，而对其他3／4情况只需使用1个随机数，不需要进行比较.但是在这2个改进方法中，确定属于需要使用第2个随机数情况需要增加1次比较.也就是说利用上述2种改进的Alias方法1次抽样分别需要使用1.5，1.25个随机数和1.5，1.25次比较（依概率的意义）.

从使用随机数方面，改进方法的确具有优势.因为在许多情况下，随机数也是一种短缺的资源.Alias系列方法抽样时间比较见图3.

但从需要进行比较的次数这个指标来看，似乎这里所谓改进的抽样方法不是在前进而是在后退，尽管从图3可以得到结论，但改进的方法在计算时间上具有很大的优势.

图2 规模为40的不同随机变量的抽样时间分布

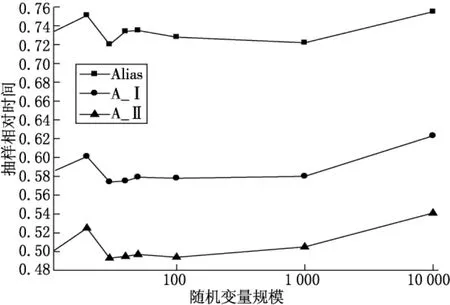
图3 Alias系列方法抽样时间比较

在Alias算法中需要进行1次实数之间的比较，而改进的Alias算法只需要进行0.5（A＿Ⅰ），0.25（A＿Ⅱ）次实数之间的比较.综合其他因素，2种对于Alias的改进算法的平均耗费时间分别大约为Alias方法的80%和70%.

上述对Alias算法的改进是以增加存储空间的耗费为代价的.对于容量为M的随机变量，直接抽样方法需要使用1个M长的整数数组和1个M长的实数数组；Alias方法需要使用2个M长的整数数组和1个M长的实数数组；A＿Ⅰ方法需要使用3个M长的整数数组和1个M长的实数数组；A＿Ⅱ方法需要使用5个M长的整数数组和1个M长的实数数组.

在对Alias算法的改进中，逐渐减少对随机数的使用，减少与随机数的比较次数.在减少随机数使用次数的同时，降低了平均抽样时间.

5 讨论

我们在这里仔细分析了著名的Alias方法，并在此基础上对其做了改进，以适当的存储空间为代价，进一步节省了抽样所需随机数和抽样所需时间.

不仅如此，可以看出，沿着这里给出的思路，可以继续减少对随机数的使用，减少与随机数的比较次数，以达到节省资源的目的，但是同时也要考虑到对存储空间的消耗.

［1］ 裴鹿成，张孝泽.蒙特卡罗方法及其在粒子输运问题中的应用［M］.北京：科学出版社，1980：58.

［2］ 上官丹骅.任意分布抽样程序的设计与实现［J］.计算机工程与应用，2004，7：107-109.

［3］ WALKER A J.New fast method for generating discrete random numbers with arbitrary frequency distribution［J］.Electronic Letters，1974，10：127-128.

［4］ WALKER A J.An efficient method for generating discrete random number with general distribution［J］.ACM Trans Math.Software，1977，3：253-256.

［5］ KRONMAL R A，PETERSON A V.On the alias method for generating random variables from a discrete distribution［J］.Amer Statist，1979，4：214-218.

［6］ DIETER U.An alternative proof for the representation of discrete distributions by equiprobable mixtures［J］.J Appl Prob，1982，19 ：869-872.

［7］ FISHMAN G S.Monte Carlo concepts，algorithms，and applications［M］.New York：Springer，1995：165-169.

Alias algorithm and improved in the random sampling

JIA Wen-bao1，WANG Zhong－qi2，ZHANG Ben-ai3

（1.Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China；
2.China Institute of Atomic Energy，Beijing 102413，China；
3.Beijing Application Physics and Computational Mathematics Research Institute，Beijing 100088，China）

Based on the generalizability theory（or the classical probability model），the famous Alias sampling method has been improved for reduce the using times of random numbers and the sampling time.A small increase in the storage space for the cost，the average using time of the improved method is 75%and 62.5%to Alias method's，and the average sampling time of the improved method is about 80%and 70%to Alias method's.

Alias algorithm；improving；random sampling

O242.1

110·61

A

1000-1832（2012）01-0023-05

2010-11-05

江苏省博士后基金资助项目（0602034B）.

贾文宝（1968—），男，博士，副教授，主要从事核信息处理及核技术应用研究；通讯作者：王仲奇（1962—），男，研究员，主要从事计算物理研究.

石绍庆）