一种基于连续属性离散化的知识分类方法

孙英慧，孙英娟，蒲东兵，姜 艳

（1.吉林师范大学计算机学院，吉林 四平 136000；

2.长春师范学院计算机科学与技术学院，吉林 长春 130032；

3.东北师范大学计算机科学与信息技术学院，吉林 长春 130117）

一种基于连续属性离散化的知识分类方法

孙英慧1，孙英娟2，蒲东兵3，姜 艳2

（1.吉林师范大学计算机学院，吉林 四平 136000；

2.长春师范学院计算机科学与技术学院，吉林 长春 130032；

3.东北师范大学计算机科学与信息技术学院，吉林 长春 130117）

提出一种基于连续属性离散化的知识分类方法.将条件属性按照重要度由高到低排序，并依照此排序将决策表中各条件属性依次离散化.在对决策表中条件属性的离散化过程中充分考虑已离散化的条件属性及决策属性，离散后的决策表不需要进一步约简.使用了模拟数据和UCI机器学习数据集中的数据进行算法测试，而且与其他离散化算法进行了对比，结果充分证明了新方法的有效性.

粗糙集；离散化；属性重要度；区间划分；断点

粗糙集是一种主要用于分析具有不确定性数据的数学理论，被广泛应用于模式识别、机器学习、数据挖掘、知识获取、知识发现等研究［1－2］.粗糙集只能对离散化的数据进行处理，因此连续属性的离散化非常关键.目前关于数据的离散化方法有很多，如等距或等频法［3］、基于统计的方法［4－5］、基于属性重要度的方法［6］、基于计算智能的方法［7－10］等.其中等距或等频法应用起来很方便，但是可能导致离散点过多，丢失信息.基于属性重要度的方法和基于计算智能的方法是应用比较广泛的方法.本文提出的连续属性离散化方法，在充分考虑属性重要度的同时，也考虑决策分类，离散后的决策表不需要约简.与其他算法相比，具有极高的识别率、最低的误识率和拒识率，产生尽可能少的断点，生成最少、最优的规则集.

1 离散化相关概念

1.1 离散化描述

具有条件属性和决策属性的知识表达系统S＝（U，A，｛Va｝，f）称为决策表.对于∀x∈U，有序列C（c1（x），…，cn（x）），D（d1（x），…，dm（x）），其中U为非空有限集，称为域；A为非空有限集，称为属性集合；Va为属性a∈A的值域；f：U→Va为一单射，使论域U中任一元素取属性a在Va中的某一唯一值；A＝C∪D，C∩D＝Ø；｛c1（x），…，cn（x）｝称为条件属性集，｛d1（x），…，dm（x）｝称为决策属性集，决策规则可以表示为c1（x），…，cn（x）→d1（x），…，dm（x）.在值域Va＝［la，ra］上的任意一个断点集合｛（a，ca1），（a，ca2），…，（a，cak）｝定义Va上的一个分类Pa：

若某一条件属性的值域被划分为n个区间，每一个断点即是一个区间端点，断点数应为n－1.离散化实质上即是利用选取的断点来对条件属性的值域进行划分，每一划分区间对应一个离散值，一般为一个整数.这样原有属性中同属于一个划分区间的各属性值合并为一个，用同一离散值代替.因而，离散化过程即是选取断点的过程.

1.2 属性重要度

在决策表中，条件属性与决策属性之间的关联程度反映了条件属性的重要性.因此，条件属性a取得某个属性值Va时，决策属性的可能值数目就反映了条件属性相对于对决策属性的重要性.如果条件属性a取得某个属性值Va时，决策属性的可能值数目唯一，则说明该条件属性值能够唯一确定该决策属性，因此在规则生成时，当条件属性取该值时不需要考虑其他条件属性.

从定义可以看出，在一个决策系统中，Ma的值越大，说明a属性的决策能力越强.

2 基于决策属性的连续属性离散化算法

2.1 算法的主要思想

决策表中的每条记录就是一条决策规则，训练样本数据并没有广泛的决策意义.通过属性离散化能将各样本之间的共同点找到，得出有意义的决策规则［10］.在本文算法中，首先运用C-mean方法将原决策系统中的各连续属性离散化，然后计算决策表中各条件属性的重要度，并将其按重要度由高到低排序.重要度最高的属性保留C-mean方法的离散化结果，其他属性根据重要度排序，依次离散化.离散化过程中充分考虑已离散化的各属性及决策属性，所有的连续属性离散化后得到新的决策系统.最后去除新的决策系统中的矛盾规则，以保证系统的识别准确率.

2.2 算法描述

在一个决策系统中，决策规则通常与重要度高的条件属性相关性更高，即重要度高的属性决策能力更强.算法描述如下：

算法：一种基于连续属性离散化的知识分类方法.输入：训练样本集D.

输出：决策规则表Snew.

令：S＝（U，A，｛Va｝，f），条件属性数目为n，决策属性集为｛d｝，S′和Snew与S具有相同结构，初始值为空.

（1）将样本集D预处理后，输入决策系统S.

（2）S′＝S，i＝1.

（3）将S′的各条件属性用FCM聚类方法离散化，令聚类中心数为k（决策分类数）.

（4）计算S′中各属性的重要度，并按照属性重要度由高到低排序各条件属性，令各条件属性排序为C1，C2，…，Cn.

（5）将S′的C1属性列赋值给Snew.

（6）i＝i＋1.

（7）判断Snew中条件属性取值相同的各行，决策属性值是否相同.分别执行（a）或（b）.

（a）若条件属性值相同时，决策属性值唯一，则取该条件属性值的各行其余连续属性不再需要离散化，如果Snew中所有的条件属性都无需离散化或者i＞n，则转至（9）；

（b）否则，将Snew中条件属性值相同的各行划分为一组.组内计算取得每一个决策值时，S中对应的i划分区间，求各划分区间的并（若划分区间有交集，则增加断点）.将各组的划分区间进行归并，最后生成i条件属性的划分区间，离散化i属性，将离散化结果添加到Snew.

（8）i≤n转至（6）.

（9）生成规则集，即将Snew中冲突行重新离散化，最后去除Snew中重复行.

2.3 区间划分

离散化即是对属性区间的划分，如果区间划分过细，就会导致分类规则过细，决策规则增加；相反，如果区间划分过粗就会导致分类不清，出现矛盾规则.本文提出两个概念：已划分区间和空闲区间.

定义2 在数轴上，已经有属性取值划分的区间称之为已划分区间.

定义3 在数轴上，没有属性取值的区间称之为空闲区间.

2.3.1 组内划分区间

若条件属性值相同时，决策属性值唯一，则取该条件属性值的各行其余连续属性不再需要离散化，否则，将Snew中条件属性值相同的各行划分为一组.因此在Snew中同一组的各行条件属性取值相同，而决策属性值并不完全相同，即存在不一致数据.令第x小组内决策属性种类为Numdx，则其对S中i的划分区间至少为Numdx个，若划分区间存在交集，增加一个划分区间.两个划分区间a，b的相交情况只有如下两种情况：此时原有区间划分转变为a′，b′，c′.如图1所示.

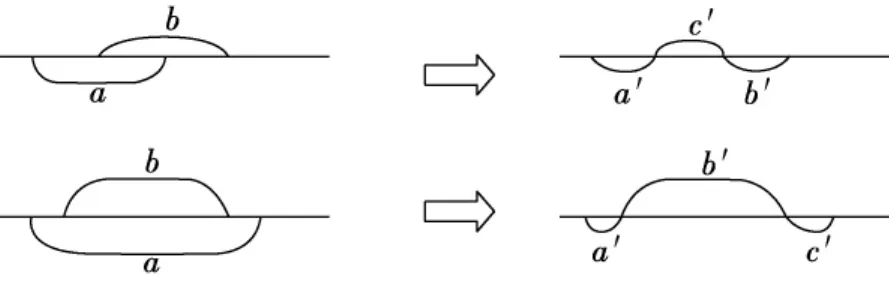
图1 组内区间划分

2.3.2 各组划分区间归并

令数轴O存放i的最后区间划分，初始值为空闲区间.首先用第一小组的区间划分划分O.然后依次将第二小组的区间划分与O归并，……直到所有小组的区间划分与O归并.因为各小组间不存在不一致数据，因此，各小组划分区间与O进行归并时，在不导致数据产生不一致的前提下尽量不增加O的区间划分.每一个小组执行与O归并前，将O各区间的更新标志清空.第x小组的区间划分，与O归并的方法为：由小到大依次取x的划分区间x1，x2，…，与O归并，xi（⌊xi，1，xi，2））区间与Oj及Oj－1区间之间的关系有如图2所示的4种情形.

（a）如果Oj－1为未更新，将Oj－1设置为已更新；否则，将xi，1作为Oj－1的新断点，将Oj－1划分为左、右两个区间，并将右区间设置为已更新.

（b）将Oj－1的右端点移至xi，2，如果Oj－1为已更新，则将xi，1作为一个新断点，将Oj－1划分为左、右两个区间.

（c）如果Oj－1为未更新，则将Oj－1的右端点移至xi，2；否则，将Oj的左端点移至xi，1，并将Oj标志为已更新.

（d）将Oj的左端点移至xi，1，若xi右端点落在O的划分区间，则将该划分区间设置为更新.

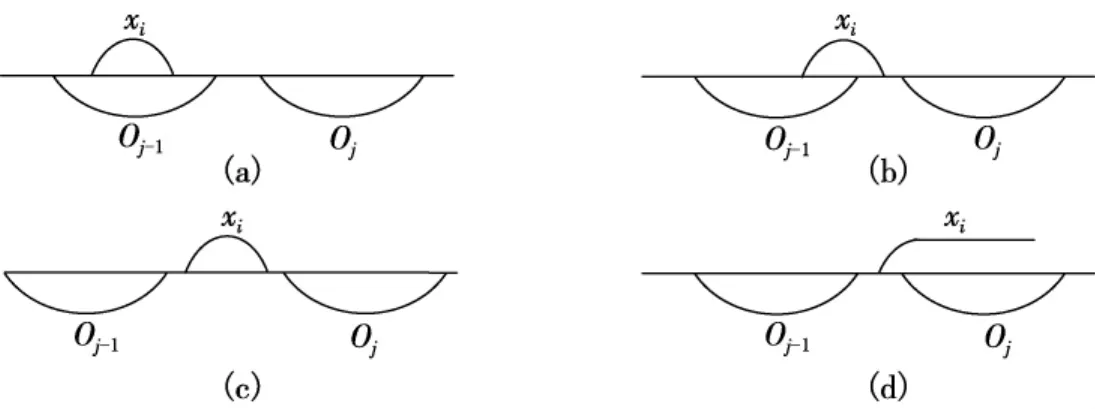
图2 属性区间划分

2.3.3 去除冲突规则

找到Snew中有冲突的两行记录，按照属性重要度，依次比较原决策系统中对应的属性值，找到两行记录首次出现不同的属性值.获得该属性的新断点D（取两条记录对应属性值的均值）.令Snew中该属性的断点序列为D1＜…＜Di－1＜Di＜…，Di－1＜D＜Di，如果原决策表S中没有记录属性取值在［Di－1，D）区间，并且更新断点后不会产生新冲突行，则将Snew中Di－1断点变更为D；否则如果决策表S中没有记录属性取值在［D，Di）区间，并且更新断点后不会产生新冲突行，则将Snew中Di断点变更为D.如果前面所述条件都不能满足，则将D作为该属性的一个新断点.按照该方法，将所有冲突行的相应属性重新离散化.运用更新后的断点集去重新离散S，得到Snew.

3 算例

3.1 模拟数据

本文选取来自文献［11］的决策表，并将本文算法与贪心算法、属性重要性离散化算法和遗传算法进行比较［10－11］，离散化结果如表1所示，断点结果如表2所示.从表1和表2可以看到，本文所提出的连续属性离散化方法只有3个断点，与遗传算法和属性重要性离散化算法的断点数相同，优于贪心算法，获得了最少的断点集.属性重要度排序为a，b；重要度分别为0.75和0.5.

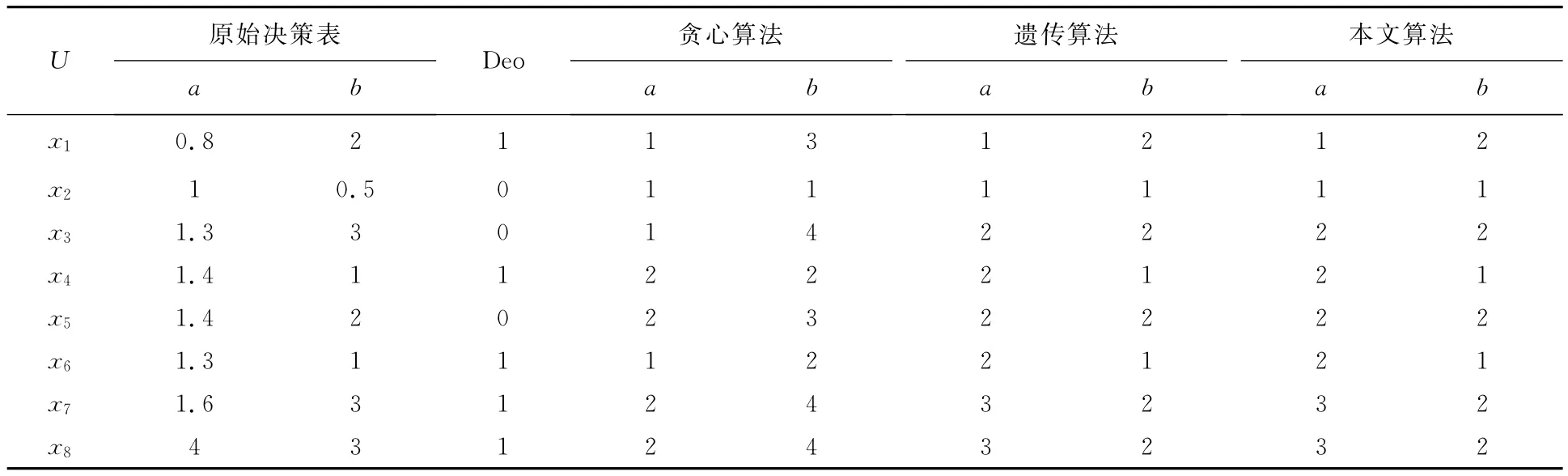
表1 不同算法离散化结果对比

表2 不同算法的离散化断点结果

3.2 UCI数据

为了验证算法的可行性和有效性，采用UCI机器学习标准数据集中的数据作为测试数据［12］.数据集的特征如表3所示.

表3 实验数据集

按训练集与测试集分别占60%及40%，独立运行100次，求得分类精度的平均值.与文献［12］中表5的各算法进行比较，结果如表4所示.其中：AEFD为文献［12］提出的一种近似等频离散化方法；A2为基于混合概率模型的无监督离散化算法；MDL为有监督离散化方法Fayyad＆Irani的MDL方法.

实验结果表明，本文提出的基于连续属性离散化的知识分类方法，在4个数据集上的识别精度都高于其他三种算法，而对Breast数据集的分类识别率更是达到99%以上，实验效果非常好.

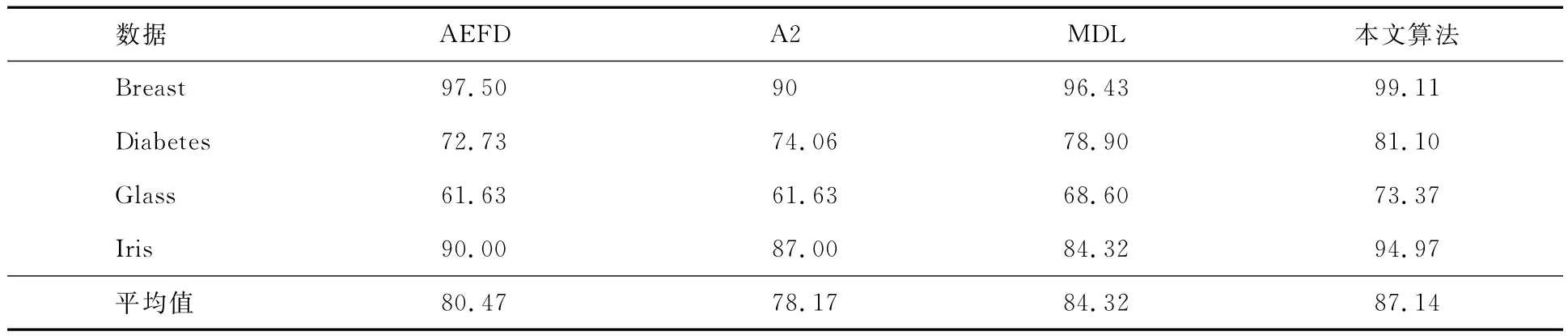
表4 识别精度比较%

4 结论

本文提出一种基于连续属性离散化的知识分类方法.通过属性重要度确定属性离散化次序，离散化过程中始终以决策分类为核心，充分考虑已经离散化的条件属性.从表1可以看出，本文提出算法的断点数明显低于文献［11］提出的贪心算法，与文献［10］提出的遗传算法和属性重要性离散化算法的断点数相同.从表4可以看出，算法在UCI的4个数据集（Breast，Diabetes，Glass，Iris）上运行所得的分类精度远高于文献［12］中表5的各分类算法.综合以上实验结果，可以看出：使用本文算法，条件属性离散后产生的断点数少，能够更好地抓住样本共性，从而分类精度更高.

［1］ 李永敏，朱善君，陈湘晖，等.基于粗糙集理论的数据挖掘模型［J］.清华大学学报：自然科学版，1999，39（1）：110-113.

［2］ PAWLAK Z.Rough sets［J］.International Journal of Information and Computer Science，1982，11（5）：341-356.

［3］ 蒋盛益，李霞，郑琪.一种近似等频离散化方法［J］.暨南大学学报：自然科学版，2009，30（1）：31-34.

［4］ MEHMET ACI，CIGDEM INAN，MUTLU AVCI.A hybrid classification method of k nearest neighbor，Bayesian methods and genetic algorithm ［J］.Expert Systems with Applications，2010，37：5061-5067.

［5］ 刘丰年，黄景涛.基于分布率的连续属性二次离散化算法［J］.微电子学与计算机，2009，26（1）：177-179.

［6］ 白根柱，裴志利，王建，等.基于粗糙集理论和信息熵的属性离散化方法［J］.计算机应用研究，2008，25（6）：1701-1703.

［7］ 王飞，刘大有，薛万欣.基于遗传算法的Bayesian网中连续变量离散化的研究［J］.计算机学报，2002，25（8）：794-800.

［8］ 刘德玲，马志强.基于多群体遗传算法的非线性最小二乘估计［J］.东北师大学报：自然科学版，2011，43（1）：40-47.

［9］ YOON-SEOK CHOI，BYUNG-RO MOON，SANG YONG SEO.Genetic fuzzy discretization with adaptiv ntervals for classification problems［C］／／GECCO.Proceedings of the genetic and Evolutionary Computatin Conference，Wahington，DC，2005：2037-2043.

［10］ 陈果.基于遗传算法的决策表连续属性离散化方法［J］.仪器仪表学报，2007，28（9）：1700-1705.

［11］ 王国胤.Rough集理论与知识获取［M］.西安：西安交通大学出版社，2001：24-105.

［12］ 蒋盛益，李霞，郑琪.一种近似等频离散化方法［J］.暨南大学学报：自然科学版，2009，30（1）：31-34.

One method of classification based on discretization of continuous attributes

SUN Ying-hui1，SUN Ying－juan2，Pu Dong-bing3，JIANG Yan2

（1.College of Computer，Jilin Normal University，Siping 136000，China；
2.College of Computer Science and Technology，Changchun Normal University，Changchun 130032，China；
3.College of Computer Science and Information Technology，Northeast Normal University，Changchun 130117，China）

This paper gives a new method of classification based on discretization of continuous attributes.Firstly condition attributes are sorted in descending order by their significance，and then each condition attribute in the decision table is discretized in sequence by the order.Both discretized condition attributes and decision attributes are paid more attention during the course of discretization.And the discretized decision table needs not to be reduced further.Finally，the simulation data and the UCI machine learning data are used to verify the new method，and the new method is compared with other discretization algorithms.The results fully show the correctness and effectiveness of the proposed method of classification based on discretization of continuous attributes.

rough set；discretization；significance of attributes；region division；breakpoint

TP 18

520·20

A

1000-1832（2012）01-0045-05

2011-05-11

国家自然科学基金资助项目（60673099，60873146）；吉林省科技发展计划项目（201105056）；吉林省教育厅科技计划基

金资助项目（2007172，2010383）；长春师范学院校内青年基金资助项目（010，012）.

孙英慧（1975—），女，硕士，讲师，主要从事数据挖掘、人工智能研究；通讯作者：蒲东兵（1970—），男，博士，副教授，主要从事嵌入式、模式识别、人工智能研究.

陶 理）