C波段转发测轨系统测站偏差的标校

宋小勇，毛 悦，贾小林

西安测绘研究所，陕西西安710054

C波段转发测轨系统测站偏差的标校

宋小勇，毛 悦，贾小林

西安测绘研究所，陕西西安710054

C波段转发测轨体制在GEO卫星测定轨中有突出优势，但其测量系统偏差的标校精度对定轨结果影响显著。基于L波段载波相位多星定轨结果，提出一种基于标准轨道拟合残差的系统偏差标校方法。该方法能够同时标校测量偏差及时标偏差，有利于弥补激光测距标校方法观测量较少的缺陷。利用国内监测站对中国导航卫星实测数据分析结果表明，经过标校后的C波段转发测轨精度可优于5 m，测量偏差及时标偏差具有较好的稳定性。

精密定轨；同步卫星；转发式测距；系统偏差

1 引 言

我国卫星导航系统采用GEO卫星作为导航星座，尽管GEO卫星具有对地连续可视的优势，但由于GEO卫星相对地面测站运动速率较小，轨道钟差参数相关性较强；同时卫星需要定期进行轨道机动［1－2］，因此造成传统GPS采用的L波段多星定轨方法在GEO连续精密定轨方面存在许多弊端。文献［3］提出了测定GEO卫星轨道的3种方法，但这些方法精度不能满足导航卫星需求。C波段转发测距体制是我国学者针对GEO卫星特点而设计的一种测轨技术，先期分析结果表明，该技术测量噪声可小于0.1m，且受气象条件影响小，是一种有潜力的测量手段［4］。C波段转发测距包含多项系统误差，通常认为，测站偏差及卫星转发时延两项系统误差是主项。针对这两项误差的标定方法国内外学者有系统研究。文献［5—7］采用残差分析方法，只能标定测站偏差相对量；文献［1，8—9］借助激光测距技术采用并置站比较法和组合定轨法，表明能将系统偏差标校精度提高到亚米级。但由于GEO卫星轨道高度较高，且激光观测受天气影响，有效数据较少，使得该方法实用性受限。文献［10—11］开展了L波段伪距数据与C转发数据组合定轨研究，但受限于伪距观测量精度，该方法标校精度不理想，且难以标定测站时标偏差。文献［12—16］针对激光观测量给出利用定轨残差拟合测量系统偏差的方法，为测量时标偏差的标校指明了思路。文献［17］通过对系统误差特点分析，给出利用移动窗口借助残差拟合确定系统偏差参数的方法，该方法也适用于C转发数据系统误差确定。考虑到卫星三维位置与测站偏差相关性更强，借助L波段载波相位多星定轨结果，本文开展了利用标准轨道标校C波段转发测距系统误差的研究工作。该方法不但能准确标定测量偏差，而且能标校时标偏差。

2 偏差参数解算原理

2.1 C波段转发测距原理

C波段转发测距原理如图1所示。

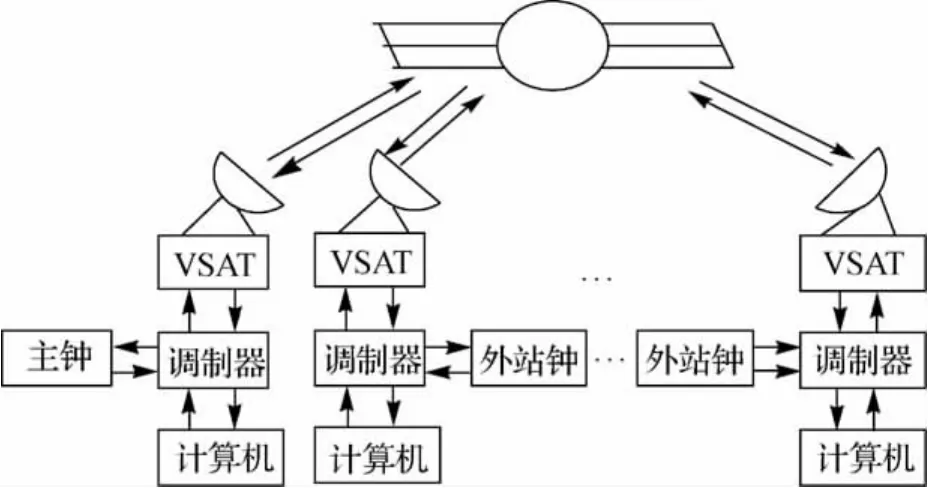
图1 C波段转发测距模式原理图［5］Fig.1 The figure of C transfer system［5］

在每个地面站放置原子钟，利用地面站原子钟产生的高精度时间信号，用不同伪码调制，同时向同一颗卫星发射相同载波的伪码扩频信号，经卫星转发器转向各卫星地面站，每个地面站接收所有台站发送的时间信号，测定信号路径的延迟，从而确定地面站到卫星的距离［18］。主要误差源除了对流层、电离层等路径相关误差外，还包括卫星转发时延、地面站测量偏差等因素。其中卫星转发时延、地面站测量偏差的准确标定是保证转发式测定轨体制观测精度的关键技术。

2.2 利用标准轨道标校测站偏差原理

C波段转发测距观测方程可写为

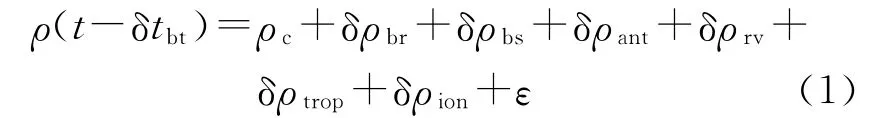
式中，ρ（t－δtbt）、ρc分别为测量时刻C波段测距观测量和理论星地距；δtbt为测站时标偏差，以s为单位；δρbr、δρbs、ε分别为测站测量偏差、卫星转发时延参数以及测站测量噪声，均以m为单位；δρant、δρrv分别为卫星及测站天线相位中心改正；δρtrop、δρion分别为对流层及电离层时延误差。对流层改正采用SAAS模型，经过模型修正后残余误差小于8cm；而电离层时延对C波段影响在厘米级，可计入测量噪声［5］。对上式进行线性近似，观测方程可写为

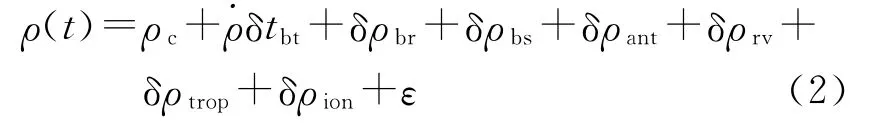
如果卫星准确位置即标准轨道能够通过其他技术精密确定，利用标准轨道和测站位置信息计算出理论星地距ρc、进行卫星及测站天线相位中心改正及对流层改正后，基于公式（1）可得到测站以及时标偏差参数观测方程

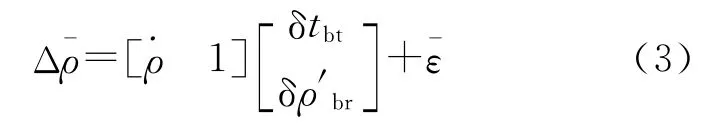
3 试验结果及分析

为了验证上述标校方法的合理性，利用北斗导航卫星2011－06－10—2011－06－16期间国内长春、临潼、喀什、北京、海南、四川、新疆7个C波段转发测轨站对GEO 3卫星实测数据进行试验计算。为得到标准轨道，同时采集同期国内临潼、长春、乌鲁木齐等12站L波段伪距及载波相位观测数据。考虑到2011－06－13T9：00～10：00该星中间有轨道机动，分为2011－06－10—2011－06－12以及2011－06－14—2011－06－16的12时两段分别进行试验计算。试验分为标准轨道确定、测站偏差标校及定轨试验结果分析3部分。

试验采用的卫星动力学模型包括：地球引力场选择10阶次JGM3模型，日月星历采用JPL DE405星历，太阳光压采用GPS T20模型加经验力补偿，同时考虑固体潮、极潮等影响。

C转发数据观测模型见前节。L伪距相位数据观测模型包括：对流层采用SAAS模型加分时段估计校正参数形式，电离层采用双频消除，同时考虑测站潮汐改正及卫星钟相对论改正。采用非差方法解算钟差参数。

3.1 标准轨道确定

首先利用非机动期间国内7个地面监测站及5个监测评估站对现有北斗卫星L波段伪距及载波相位数据分别进行多星定轨，多星定轨原理见文献［19—20］。两类不同测轨站对GEO3卫星定轨结果的互差如图2。统计结果表明轨道面径向（R）、沿迹（T）及法向（N）误差分别为0.347m、1.859m、0.712m。轨道三维位置误差小于3m。除了上述不同测站定轨结果互比方法外，轨道重叠弧段法、激光检核法及星地双向时间同步数据检核法也是评价定轨精度的有效手段。由于在本次试验期间GEO 3星没有激光观测数据，同时也没有足够弧段测量数据（连续4d以上）进行重叠弧段试验，这些评估方法缺乏实施条件。对比文献［19—20］结果看出，上述定轨结果与该文献相同测站的结论一致，代表了目前国内区域站定轨水平，可以作为参数标校的标准轨道。

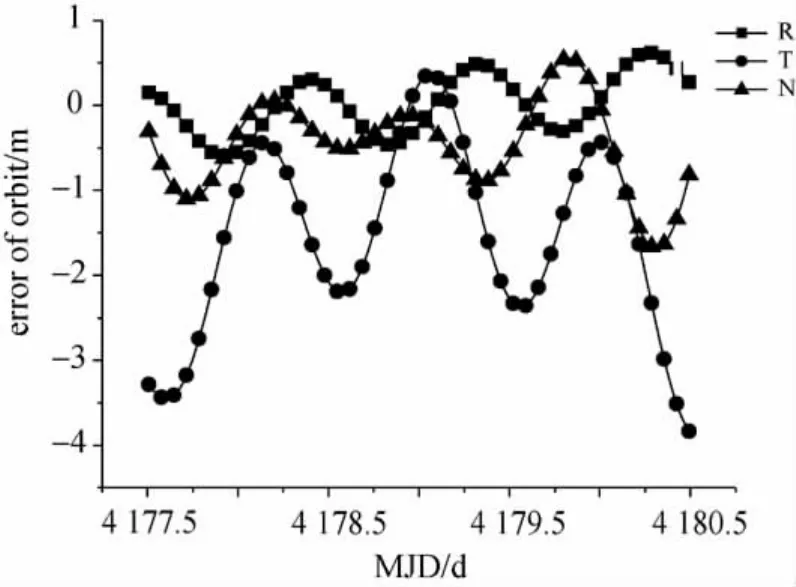
图2 7站及5站测轨方案轨道互差图Fig.2 The difference between the orbit determination result by 7stations and 5stations

3.2 测站偏差标校

为了分析比较不同种测站偏差估计方案的合理性，分别设计了3种试验方案。3种方案均以7个C波段测轨站实测数据作为原始观测量，估计参数为测量偏差参数和时标偏差参数，卫星转发时延参数合并到测站偏差参数中计算。卫星天线相位中心、测站位置偏心、对流层等误差均进行了修正。试验方案：方案1估计7个测站测量偏差参数；方案2估计7个测站测量偏差参数及时标偏差参数；方案3估计4个测站测量偏差，同时估计其他3个测站测量及时标偏差（表1～2）。

由方案1结果看出，仅估计测站偏差而不估计测站时标偏差，拟合残差均大于2m，远远超过C波段转发测距噪声0.2m，说明残差中仍含有系统误差。

对比方案1和方案2统计结果看出，同时解算测量偏差及时标偏差参数，数据拟合残差均小于0.246m。长春、临潼、喀什（授时）3站均有接近2s的时标偏差，其他4站测量时标偏差小于0.07m。考虑到GEO 3卫星相对中国区测站视向距离变化率˙ρ最大不超过10m／s，利用观测噪声和式（3）可近似估计出测站时标偏差解算精度在0.1s量级，因此，可认为北京、海南、新疆和四川4站没有时标偏差。

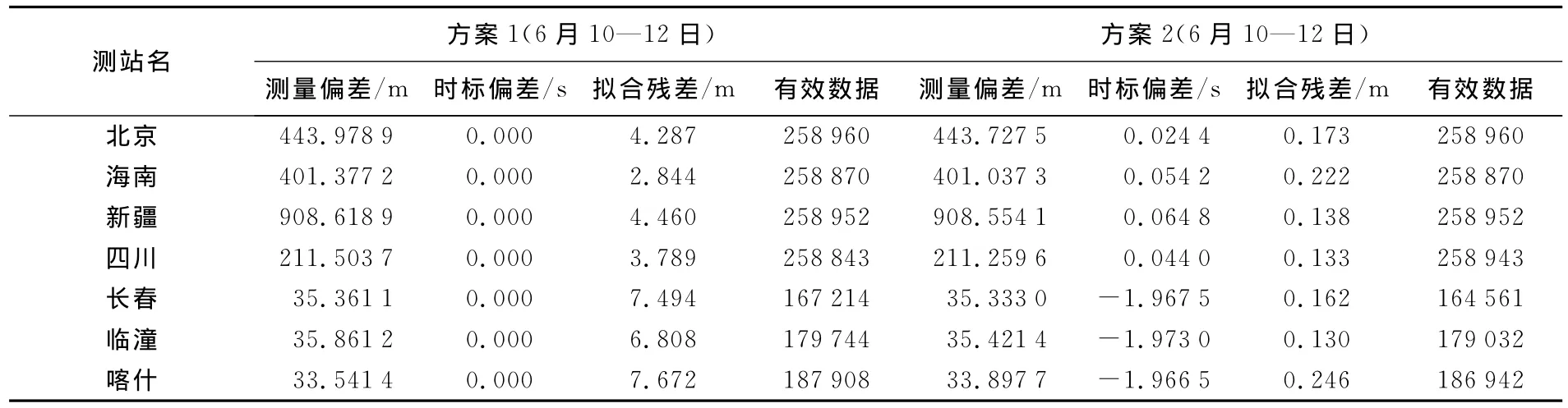
表1 方案1、方案2解算结果统计表Tab.1 The estimated parameter from scheme 1and 2

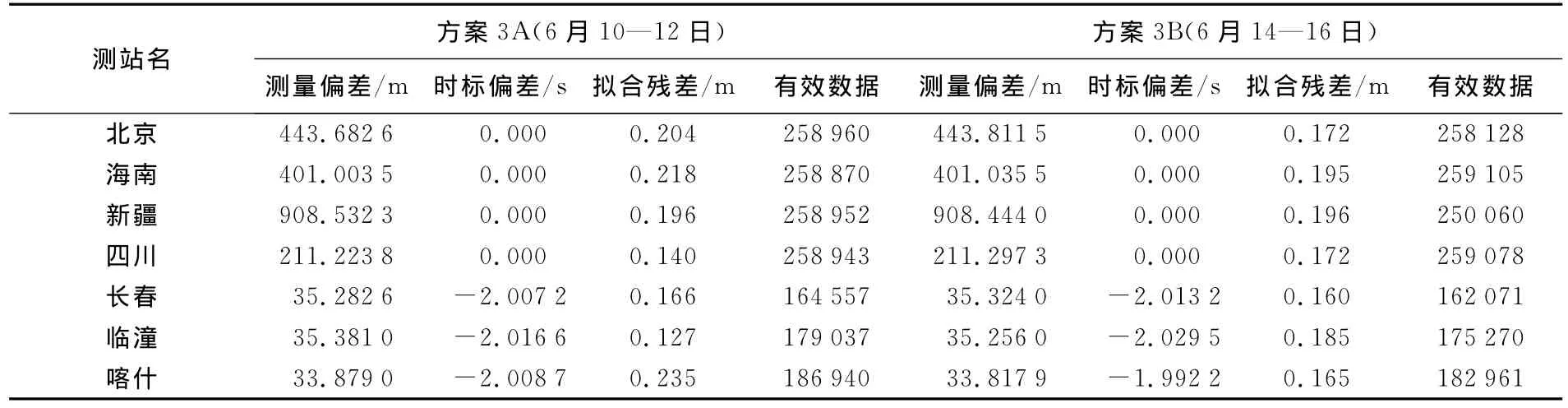
表2 方案3解算结果统计表Tab.2 The estimated parameter from scheme 3

对比方案2与方案3A结果看出，当不解算北京、海南、新疆和四川4站时标偏差时，方案3A定轨拟合残差与解算时标偏差时的方案2结果相比较，并没有明显差异。这进一步证实北京、海南、新疆和四川4个测站没有时标偏差。

为证实测站偏差与时标偏差参数的相对稳定性，基于6月14—16日12时上述7个站C转发测距实测数据采用方案3进行了偏差解算试验。统计结果如方案3B。对比方案3B与方案3A结果看出，不同时段解算的测站偏差和时间偏差具有很好的一致性。一方面验证了解算结果的准确性，另一方面表明测站偏差随时间变化相对较小，因此，非机动时段确定的测站偏差可用于机动期间定轨。

3.3 定轨结果分析

为了验证上述C波段转发测距系统偏差标校精度。基于上述标校的系统误差分别进行了精密定轨试验。试验分为L、C波段组合定轨、固定测站时标偏差条件下的C独立定轨以及解算测站时标偏差条件下的C独立定轨3种。

3.3.1 L／C组合定轨结果

组合2011－06－10—2011－06－12国内5个评估站3天L波段伪距和载波相位数据，以及上述国内7个站C转发测轨数据定轨，定轨中C转发测轨数据的测站偏差以及时标偏差均采用方案3A标校值。定轨结果与同期国内5个评估站L波段多星定轨结果互差见图3。其中图3（a）为6月10—12日结果，图3（b）为6月14—16日结果。

统计结果表明，组合定轨在R、T、N 3方向误差分别为0.938m、1.755m、1.626m。

图3 LC组合定轨结果Fig.3 The result of the orbit determination by transfering and carrier

对比标准轨道位置误差图2与图3看出，L波段伪距相位数据与C转发数据组合定轨结果与L独立定轨结果精度相当。C转发数据对组合定轨精度的贡献还需要激光、星地双向时间同步等外符合观测手段进一步验证。

3.3.2 C独立定轨结果

利用2011－06－10—2011－06－12国内7个C波段转发测轨站数据定轨，测站时标偏差及测量偏差参数见方案3A。C定轨结果与同期国内5个评估站L波段多星定轨结果互差见图4（a）。

统计结果表明，C波段转发数据独立定轨结果与L波段标准轨道比较，在轨道R、T、N 3个方向互差分别为：1.131m、2.512m、4.210m，三维位置差小于5m，比L波段独立定轨结果稍差，分析认为，主要由于C波段转发测距观测量精度约为0.1m量级，比L波段载波相位数据测量精度差。

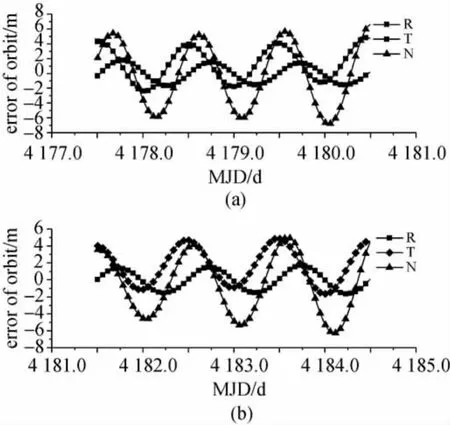
图4 C定轨结果Fig.4 The result of the orbit determination by transfering

由于方案3A在标校测站偏差与时标偏差时采用了2011－06－10—2011－06－12国内5个评估站确定的标准轨道，基于该偏差的C波段转发定轨结果与L波段标准轨道有一定相关性，两者互差不能完全证明标校结果的可靠性。因此，采用2011－06－14—2011－06－16上述7站C转发测轨数据独立定轨，距离偏差及时标偏差同样采用方案3A标校值。C定轨结果与L波段标准轨道互差如图4（b）。

统计结果表明，6月14—16日C转发数据定轨结果与L波段标准轨道比较，在轨道R、T、N这 3个方向互差分别为：1.125m、2.683m、3.520m，轨道精度与6月10—12日相当，三维位置差小于5m，反映了C波段转发数据独立定轨精度水平。

为了进一步从定轨结果验证解算测站时标参数的合理性。完全不考虑测站时标误差，仅采用方案1计算的测站测量偏差参数以及2011年国内7站C波段转发测距观测量独立定轨，将定轨结果与L波段标准轨道比较，互差见图5。

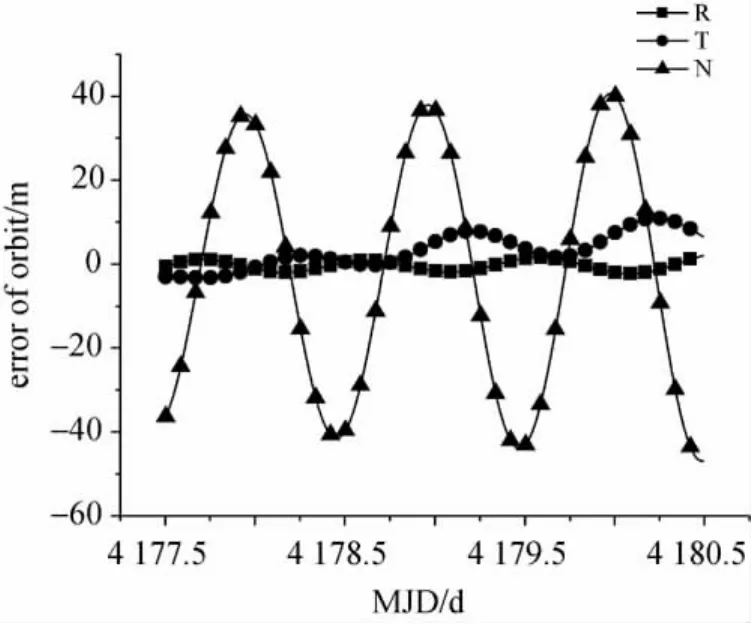
图5 6月10—12日C定轨结果（不考虑时标偏差时）Fig.5 The result of the orbit determination by transfering during 2011－06－10—2011－06－12without time bias parameter

由图5看出，如果不考虑长春、临潼、喀什3测站时标误差影响，C定轨结果在轨道面法向存在显著误差，表明3站观测量存在时标偏差。上述图4、图5定轨结果统计比较见下表3。

表3 定轨结果统计表Tab.3 The statistics table of orbit determination m

需要指出的是，C波段转发测距数据时标偏差可能与设备标校不准确有关。如果测量设备经过准确标校后，如果解算的时标偏差参数量级小于0.1s，参考3.2节分析，可认为测站不存在时标偏差。

4 结 论

C波段转发测距是跟踪测量同步卫星的有效手段。测量系统偏差的标校误差是限制该测量体制使用的主要问题。借助L波段多星定轨结果，通过标准轨道可以实现对测量偏差及时标偏差参数的同时标校。结果表明，C波段转发测距系统测量偏差具有相对稳定性，部分C波段转发测轨站具有时标偏差，时标偏差也是慢变量。采用标准轨道标校法可以解决C波段转发测量系统误差的标校问题，标校后的C转发测轨系统区域定轨精度可优于5m。考虑到系统偏差标校后的C转发数据可用于机动卫星的连续跟踪测量，本文方法对改善GEO卫星机动定轨精度有借鉴意义。

［1］ ZHOU Jianhua，CHEN Liucheng，HU Xiaogong，et al.The Precise Orbit Determination of GEO Navigation Satellite with Multi－types Observation［J］.Science in China Series G：Physics，Mechanics and Astronomy，2010，40（5）：520－527.（周建华，陈刘成，胡小工，等.GEO导航卫星多种观测资料联合精密定轨［J］.中国科学G辑：物理学力学天文学，2010，40（5）：520－527.）

［2］ SONG Xiaoyong.Study on the Orbit Determination of Compass Navigation Satellite［D］.Xi’an：Changan University，2009.（宋小勇.北斗导航卫星精密定轨技术研究［D］.西安：长安大学，2009.）

［3］ LICHTEN S M，EDWARDS C D，YOUNG L E，et al.A Demonstration of TDRS Orbit Determination Using Differential Tracking Observable from GPS Ground Receiver［J］.Proceedings AAS／AIAA Space Flight Mechanics Conference AAS.Pasadena：［s.n.］，1993：93－160.

［4］ LI Zhigang，YANG Xuhai，AI Guoxiang，et al.A New Method for Determination of Satellite Orbit by Transfer［J］.Science in China Series G：Physics，Mechanics and Astronomy，2009，52（3）：384－392.（李志刚，杨旭海，艾国祥，等.转发器式卫星轨道测定新方法［J］.中国科学G辑：物理学力学天文学，2009，52（3）：384－392.）

［5］ YANG Xuhai，LI Zhigang，FENG Chugang，et al.Methods of Rapid Orbit Forecasting after Maneuvers for Geostationary Satellites［J］.Science in China Series G：Physics，Mechanics and Astronomy，2009，52（3）：1759－1765.（杨旭海，李志刚，冯初刚，等.GEO卫星机动后的星历快速恢复方法［J］.中国科学G辑：物理学力学天文学，2008，38（12）：1759－1765.）

［6］ HUANG Yong，HU Xiaogong，HUANG Cheng，et al. Precise Orbit Determination of a Maneuvered GEO Satellite Using CAPS Ranging Data［J］.Science in China Series G：Physics，Mechanics and Astronomy，2009，52（3）：1750－1758.（黄勇，胡小工，黄珹，等.利用CAPS测距数据确定GEO卫星变轨期间的轨道［J］.中国科学G辑：物理学力学天文学，2008，38（12）：1750－1758.）

［7］ LEI Hui，LI Zhigang，YANG Xuhai，et al.Precise Orbit Determination Experiment of Compass－GEO Based on Transponder Ranging［J］.Acta Geodaetica et Cartograohica Sinica，2011，40（Sup）：31－33.（雷辉，李志刚，杨旭海，等.基于转发式的北斗卫星导航系统地球静止轨道卫星精密定轨试验［J］.测绘学报，2011，40（增刊）：31－33.）

［8］ GUO Rui，HU Xiaogong，TANG Bo，et al.Precise Orbit Determination for the Geostationary Satellite with Multiple Tracking Technique［J］.Chinese Science Bulletin，2010，55（6）：428－434.（郭睿，胡小工，唐波，等.多种测量技术条件下的GEO卫星定轨研究［J］.科学通报，2010，55（6）：428－434.）

［9］ GUO Rui，LIU Yanyu，TAN Hongli，et al.Analysis of GEO Satellite Precise Orbit Determination Based on Selfsending and Self－receiving Ranging Data［J］.Journal of Geomatics Science and Technology，2009，26（5）：333－336.（郭睿，刘雁雨，谭红力，等.基于自发自收测距的GEO卫星精密定轨［J］.测绘科学技术学报，2009，26（5）：333－336.）

［10］ GUO Rui，HU Xiaogong，LIU Li，et al.Orbit Determination for Geostationary Satellites with the Combination of Transfer Ranging and Pseudorange Data［J］.Science in China Series G：Physics，Mechanics and Astronomy，2010，53（9）：1746－1754.

［11］ LIU Yanyu，HE Feng，QIU Weiwei，et al.Precise Orbit Determination of GEO Navigation Satellite under Support of Transfer Ranging［J］.Journal of Geomatics Science and Technology，2010，27（5）：332－336.（刘雁雨，何峰，邱巍巍，等.转发式测距数据支持的GEO导航卫星精密定轨［J］.测绘科学技术学报，2010，27（5）：332－336.）

［12］ FENG Chugang，ZHU Yuanlan，ZHANG Feipeng.LAGEOS－1 and LAGEOS－2Quicklook Residual Analysis［J］.Acta Geodaetica et Cartograohica Sinica，2001，30（3）：226－232.（冯初刚，朱元兰，张飞鹏.SLR资料的快速处理［J］.测绘学报，2001，30（3）：226－232.）

［13］ QU Feng，WANG Tanqiang，CHEN Xianjun，et al.Precise Orbit Determination of GPS 35Satellite Using SLR Data［J］.Acta Geodaetica et Cartograohica Sinica，2003，32（3）：224－228.（瞿锋，王谭强，陈现军，等.用SLR资料精密确定GPS35卫星轨道［J］.测绘学报，2003，32（3）：224－228.

［14］ ZHAO Chunmei，QU Feng，CHENG Pengfei，et al.Data Quality Analysis of Argentina San Juan Laser Ranging System［J］.Acta Geodaetica et Cartograohica Sinica，2008，37（3）：338－347.（赵春梅，瞿锋，程鹏飞，等.阿根廷圣胡安激光测距系统的SLR数据质量分析［J］.测绘学报，2008，37（3）：338－347.）

［15］ QIN Xianping，YANG Yuanxi，JIAO Wenhai，et al.Determination of Navigation Satellite Clock Bias Using SLR and Pseudorange Data［J］.Acta Geodaetica et Cartograohica Sinica，2004，33（3）：205－209.（秦显平，杨元喜，焦文海，等.利用SLR和伪距资料确定导航卫星钟差［J］.测绘学报，2004，33（3）：205－209.）

［16］ QIN Xianping，YANG Yuanxi.Geocenter Variations Derived from the Data of SLR to Lageos2［J］.Acta Geodaetica et Cartograohica Sinica，2003，32（2）：120－124.（秦显平，杨元喜.用SLR数据导出的地心运动结果［J］.测绘学报，2003，32（2）：120－124.）

［17］ YANG Yuanxi，ZHANG Shuangcheng.Fittings of Systematic Errors and Covariance Matrices in Navigation［J］.Acta Geodaetica et Cartograohica Sinica，2004，33（3）：189－194.（杨元喜，张双成.导航解算中的系统误差及其协方差矩阵拟合［J］.测绘学报，2004，33（3）：189－194.）

［18］ LI Zhigang，YANG Xuhai，LI Weichao，et al.Method of Satellite Orbit Survey with Transfer［J］.Journal of Time and Frequeney，2006，29（2）：81－89.（李志刚，杨旭海，李伟超，等.转发器式卫星测轨方法［J］.时间频率学报，2006，29（3）：81－89.）

［19］ ZHOU Shanshi.Studies on Precise Orbit Determination Theory and Application for Satellite Navigation System with Regional Tracking Network［D］.Shanghai：Shanghai Astronomical Observatory，2011.（周善石.基于区域监测网的卫星导航系统精密定轨方法研究［D］.上海：中国科学院上海天文台，2011.）

［20］ ZHOU Shanshi，HU Xiaogong，WU Bin，et al.Orbit Determination and Time Synchronization for a GEO／IGSO Satellite Navigation Constellation with Regional Tracking Network［J］.Science in China：Physics，Mechanics and Astronomy，2011，54（6）：1089－1097.

Calibrating the Station Biases for the C－Band Transfer Measuring System

SONG Xiaoyong，MAO Yue，JIA Xiaolin
Xi’an Research Institute of Surveying and Mapping，Xi’an 710054，China

The C－band transfer measuring system plays an important role in the precise orbit determination（POD）for geostationary satellite.However，the performance of the system was remarkably influenced by the accuracies of the station biases.Based on the orbits from the multi－satellite POD using the carrier observation of L－band，a new method to calibrate the biases from orbit fitting of C－band measurement is presented.This method can not only estimate the ranging biases and time biases simultaneously，but also overcome the shortcoming of too few observations when using the SLR calibrating method.The POD experiment of Compass navigation satellite shows that the satellite’s position error is about 5 m after the station biases is calibrated，and the estimated ranging biases and time biases have higher stability and reliability.

orbit determination；geostationary satellite；transfer；bias

SONG Xiaoyong（1968—），male，PhD，senior engineer，majors in the satellite navigation and positioning.

SONG Xiaoyong，MAO Yue，JIA Xiaolin.Calibrating the Station Biases for the C－Band Transfer Measuring System［J］.Acta Geodaetica et Cartographica Sinica，2012，41（4）：517－522.（宋小勇，毛悦，贾小林.C波段转发测轨系统测站偏差的标校［J］.测绘学报，2012，41（4）：517－522.）

P228

A

1001－1595（2012）04－0517－06

国家自然科学基金（41074020）

宋启凡）

2011－08－22

2012－02－24

宋小勇（1968—），男，博士，副研究员，研究方向为卫星导航与定位。

E－mail：sxyong＠21cn.com