卫星夹层结构夹芯层力学性能分析与数值模拟

李 响 游 敏

（三峡大学水电机械设备设计与维护湖北省重点实验室，湖北宜昌 443002）

夹层结构也称为三明治结构，具有高强、质轻的特点，在汽车、航天等诸多领域应用广泛.针对夹层结构的研究，目前主要集中在其结构优化设计、力学等效性能、新型结构的开发、夹层结构的高精度数值模拟等方面［1－6］.论文对蜂窝夹芯结构的力学性能进行研究，选取卫星夹层板正六边形蜂窝夹芯结构作为实例进行数值模拟分析，建立正确的蜂窝夹层结构三维模型并选择合适的单元进行计算，验证其等效力学性能分析方法的正确性和可行性，同时为卫星蜂窝夹芯结构的优化设计提供理论依据.

1 夹层结构夹芯层

夹芯是夹层结构的重要组成部分，合理的夹芯结构可以大大减轻夹层结构的重量.根据不同的应用目的和工程需求，夹芯被设计成多种结构形式，主要包括蜂窝夹芯、泡沫夹芯、桁架夹芯等.由面板层与蜂窝状夹芯层通过胶粘剂粘结成的复合材料夹层结构称为蜂窝夹层结构.蜂窝夹芯结构形状主要包括六边形、矩形、三角形、正弦曲线形等，而正六边形强度最高，因此其应用最为广泛，如图1所示.蜂窝夹层结构由于其具有高强度、高刚度、重量轻等众多优点，在航空航天领域尤其航天卫星结构中被广泛采用.

图1 六边形蜂窝夹芯结构

2 夹层结构夹芯层力学性能研究

2.1 夹层结构力学性能国内外研究成果

自从20世纪四、五十年代开始，国内外大量学者致力于夹层结构的力学性能研究，取得了大量的研究成果，建立了多种模型，主要包括位移模型、平衡模型和混合模型.其中位移模型遵循一阶剪切理论，主要包括Reissner理论模型和Hoff理论模型［4－6］.为了更好地对夹芯层的微观和宏观结构的力学性能进行研究，有必要建立一个等效模型，能从总体上同时反映夹芯结构的微观性能和宏观性能，本文称之为夹芯结构力学等效模型.蜂窝夹芯结构力学等效模型的等效过程如图2所示.

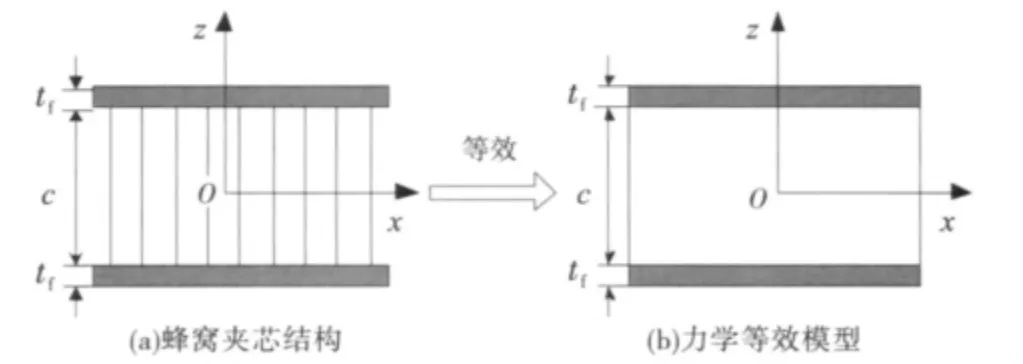
图2 蜂窝夹芯结构和力学等效模型

以Gibson［4，7］为代表的国内外学者围绕正六边形蜂窝夹芯结构力学性能做了一定的工作，建立了多种夹芯结构分析模型［8－11］，并提出了经典的胞元理论.然而已有的研究大部分只考虑了夹芯层壁板的弯曲变形，而未考虑内部正六边形或者其他形状胞元壁板的伸缩变形.同时，Gibson公式确定的弹性矩阵具有不确定性，这将导致该公式不能直接应用于工程实际.本文在已有研究的基础上，运用传统的材料力学理论知识，对六边形和方形蜂窝夹芯结构的力学等效模型进行改进分析与求解.

2.2 六边形蜂窝夹芯结构力学模型

将蜂窝夹芯层每个六边形或者方形单元定义为细胞单元体，简称胞元.六边形蜂窝夹芯胞元如图3所示.

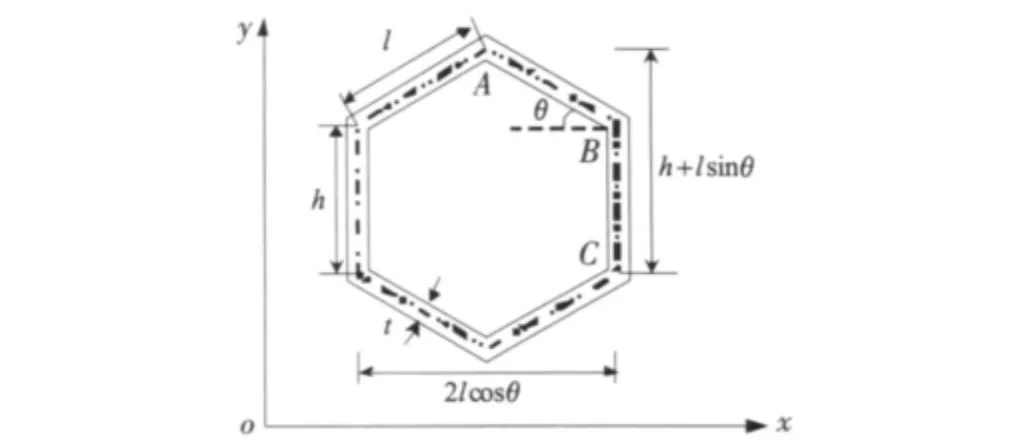
图3 六边形蜂窝夹芯胞元

在图3中，l为六边形胞元长度（mm）；h 为胞元宽度（mm）；t为胞元厚度（mm）；θ为胞元长边与宽边的夹角（°）.为了求解夹芯力学参数，使胞元模型处于单向受x 方向或者y 方向应力状态（如图4所示）.

图4 六边形蜂窝夹芯胞元受力示意图

根据力的平衡原理、材料力学梁弯曲理论和质量守恒定律等相关知识，可以求出蜂窝夹芯结构（六边形）的等效弹性参数公式为

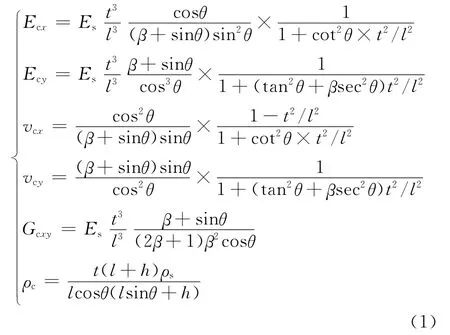
式中，β＝h／l.其他各符号的含义为：Ecx，Ecy为x，y方向上的等效弹性模量（MPa）；Es为夹芯材料的弹性模量（MPa）；Gcxy为xy 平面上的等效剪切模量（MPa）；vcx，vcy为在x，y 方向上的等效泊松比；ρc 为六边形蜂窝夹芯的等效密度（kg／m3）；ρs 为六边形蜂窝夹芯材料的密度（kg／m3）.

3 六边形蜂窝夹芯层数值模拟研究

本文选取某卫星结构［11］上采用的蜂窝夹层板作为实例，对蜂窝夹芯结构的力学性能进行仿真分析.该蜂窝夹层板的夹芯为正六边形蜂窝，具体结构数据见表1.夹芯材料铝的屈服强度为758MPa，密度为2 780kg／m3.

表1 卫星结构蜂窝夹层板夹芯结构参数

3.1 有限元模型

采用有限元分析软件Ansys建立正六边形蜂窝夹芯结构的有限元模型.为了运用有限元法求得正六边形蜂窝夹芯的等效弹性常数，单元体采用板壳单元Shell63，具体模型尺寸为0.1m×0.1m×0.024 4m，如图5所示.分别给蜂窝夹芯结构加上单向应力（σcx，0，0）T，（0，σcy，0）T和（0，0，σcxy）T及相应的约束，进行有限元数值模拟可得出其对应的应变（εcx1，εcy1，0）T，（εcx2，εcy2，0）T和（0，0，γcxy）T，同时蜂窝夹芯结构的等效弹性常数可表达为

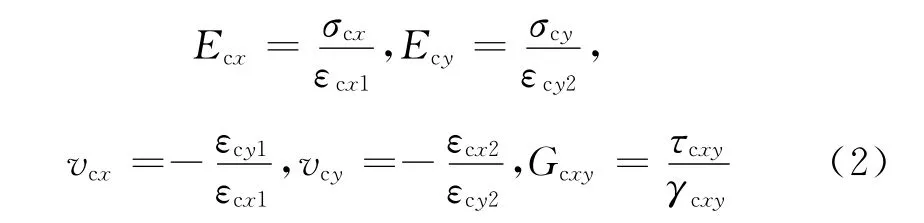
图5 正六边形蜂窝夹芯结构的有限元模型

3.2 数值模拟分析

取σcx、σcy和τcxy等于30 000Pa分别进行加载，可以得到数值模拟图如图7～12所示.

根据公式（1）理论计算和仿真分析计算（结合公式（2））分别得到卫星蜂窝夹芯结构等效模型的弹性参数见表2.

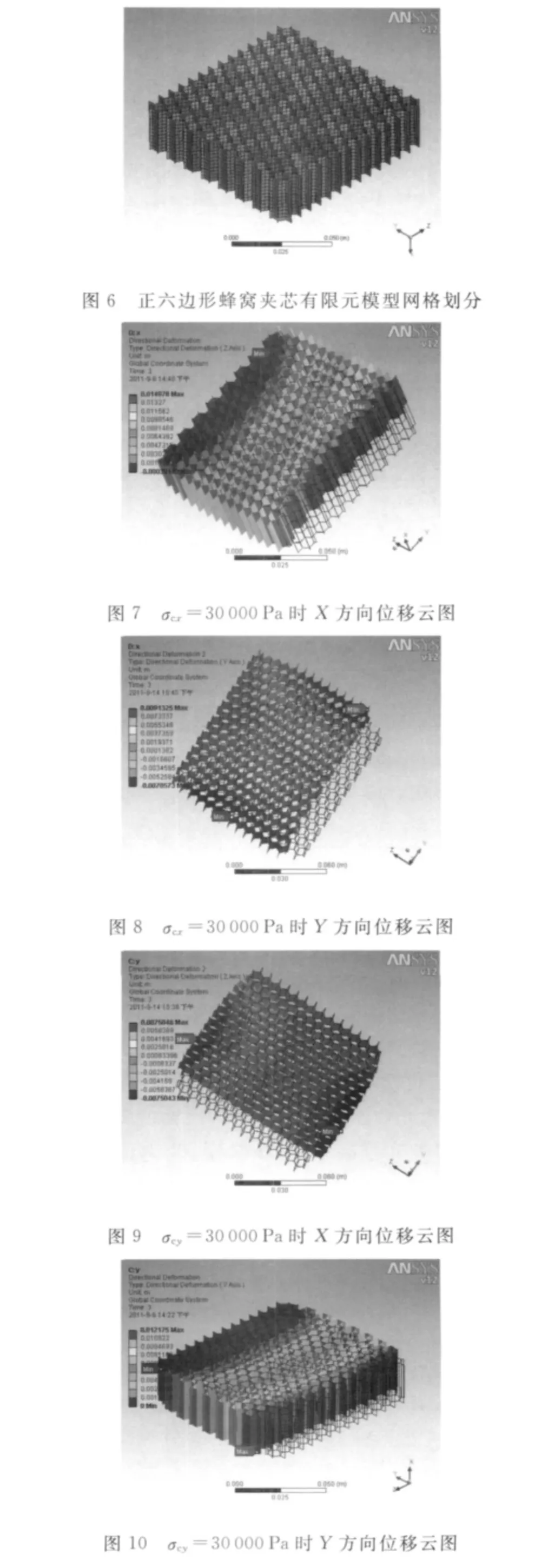
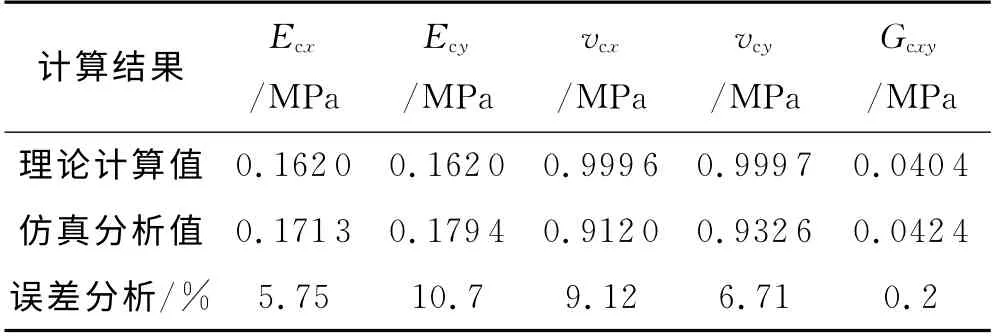
表2 六边形蜂窝夹芯结构等效模型的弹性参数

分析表2中的结果，比较理论计算值和仿真分析值，误差总体控制在10%以内.造成这种误差的主要原因在于建立正六边形铝蜂窝的有限元模型的精确度问题、单元体的选择以及网格划分的精度等方面.本文为了建模的精确，按照实际的结构尺寸进行建模（正六边形胞元在y 向的胞元壁厚是x 向的2倍），这与以往为了建模和分析简便所采用的处理方式不同（正六边形胞元壁厚取相同的值），大大提高了有限元分析的可靠性和准确性.总体来说，理论计算和仿真分析结论较为吻合，验证了蜂窝夹芯结构力学等效模型的正确性和可靠性.

4 结 语

以六边形蜂窝夹芯结构为对象，对其等效力学性能进行了研究，建立了蜂窝夹芯结构的力学等效模型，导出了六边形蜂窝夹芯结构的等效弹性常数的计算公式；以卫星夹层板正六边形蜂窝夹芯结构作为实例进行数值模拟分析，经过对比数值模拟和理论计算结果，验证了力学等效模型及其等效弹性常数的正确性，同时为卫星蜂窝夹芯结构和相类似工程结构的优化设计提供了重要的参考依据.本文的研究工作将可作为其它类型蜂窝夹芯结构的力学分析和仿真模拟的重要理论方法.

［1］ Xiang Li，Gangyan Li，Chun H.Wang and Min You.Minimum－Weight Sandwich Structure Optimum Design Subjected to Torsional Loading［J］.Applied Composite Materials，2012，19：117－126.

［2］ Xiang Li，Gangyan Li and Chun H.Wang.Optimisation of Composite Sandwich Structures Subjected to Combined Torsion and Bending Stiffness Requirements［J］.Applied Composite Materials，In Press，Published online：19July 2011：1－16.

［3］ 谭永刚.X－core夹层结构制备工艺及力学性能研究［D］.南京：南京航空航天大学，2009.

［4］ Gibson L J，Ashby M F.Cellular solids：structure and properties［M］.Cambridge：Cambridge Univ.Press，1999.

［5］ Bozkurt S B，Sezgin F E，et al.Composte Sandwch Structures；Experimental Evaluation and Finite Element Analysis of Mechancal Propertes［J］.Experimental Analysis of Nano and Engineering Materials and Structures.E.E.Gdoutos，Springer Netherlands，2007：119－120.

［6］ 李 响.承载夹层复合材料的轻量化设计方法及其应用研究［D］.武汉：武汉理工大学，2011.

［7］ Gibson L J.Modelling the Mechanical Behavior of Cellular Material［J］.Master Science and Engineering.1989，A110：1－36.

［8］ ALLEN H G.Analysis and Design of Structural Panels［M］.Oxford：Pergamon Press，1969.

［9］ 富明慧，尹久仁.蜂窝芯层的等效弹性参数［J］.力学学报，1999，31（1）：113－118.

［10］梁 森，陈花玲，陈天宁.蜂窝夹芯结构面内等效弹性参数的分析研究［J］.航空材料学报，2004，24（3）：26－31.

［11］夏利娟，金咸定，汪庠宝.卫星结构蜂窝夹层板的等效计算［J］.上海交通大学学报，2003，37（7）：999－1001.