大型电机线棒端部电场的有限元计算方法

孙永鑫， 胡春秀

(哈尔滨大电机研究所，哈尔滨 150040)

大型电机线棒端部电场的有限元计算方法

孙永鑫， 胡春秀

(哈尔滨大电机研究所，哈尔滨 150040)

由于大型电机定子线棒端部电场分布不均，造成防晕层表面易产生电晕和热老化现象。采用有限元弱解形式与多场建模相结合的方法，对大电机定子线棒端部防晕层电场及损耗密度分布进行了数值计算，并与阻容链算法进行了对比。结果表明，该算法能够避免阻容链方法所导致的算法误差，提高求解准确性;亦能有效解决传统有限元方法的建模及边界设定困难等问题，提高求解效率及精度;其防晕层损耗密度分布与电晕实验中的发热状况一致。该算法能满足具有多段非线性防晕结构的三维定子线棒端部电场计算的工程需要，可作为计算防晕结构及材料参数的理论依据，并为进一步建立优化计算模型提供基础。此外，该算法为存在表面电阻率的有限元电场计算提供思路。

定子线棒;防晕层;电场计算;非线性;弱解形式

0 引言

大型电机定子线棒端部由于电场分布不均，在实验和运行过程中，防晕层表面易产生电晕和热老化现象，严重制约着电机额定电压与单机容量的进一步提高［1］。为改善这种状况，线棒端部普遍采用多段非线性碳化硅防晕结构。这种结构能够自动均匀场强，增强线棒的耐压等级。如何准确计算多段非线性防晕结构下的电场分布，对于线棒防晕结构的设计至关重要［2－3］。

现阶段端部防晕层电场的计算有阻容链和有限元两种方法。阻容链方法是将防晕层结构简化为阻容链模型，推导出相应的非线性常微分方程，然后运用不同的数值计算方法求解。已有的研究包括二分法、龙格－库塔法［4］和有限差分法［5］等。这类方法建模简单、求解快速，无须考虑空间电场状态。不足是:无法得到转角和宽窄边等处的三维电场状况，以及主绝缘夹在半导体防晕层与导线之间，将其理解为纯电容，计算时会产生一定的误差。传统有限元方法也毫无优势［6］，原因一是防晕层表面的边界条件无法确定，若求解域包含外部空间，则只能选取特定区域，甚至整机求解［7］;二是防晕层较薄使得网格数量剧增而质量骤降，表面电阻率须转化为体积电阻率而增大误差。

笔者试图运用有限元弱解形式描述防晕层控制方程，与主绝缘准静态方程联立，求解线棒端部的电场分布，以期解决阻容链方法和传统有限元方法的不足。

1 几何模型

以额定电压26 kV的某大型发电机定子线棒为仿真对象，得到端部三维几何模型，见图1。

图1 定子线棒端部几何模型Fig.1 Geometric model of stator end-winding

该模型为三段非线性防晕结构，具体尺寸:线棒截面矩形为114 mm×28 mm，导线截面棱角半径为2 mm，线棒截面棱角半径为5 mm，单边绝缘厚度为6.6 mm;线棒直线转角和引线转角均为50°，直线转角半径为100 mm，引线转角半径为65 mm。曲线a、b、c用于显示参数分布。防晕层材料参数见表1。

表1 防晕层材料参数Table 1 Material parameters of corona protective coating

2 计算方法

2.1 控制方程

在工频交流电压下，主绝缘区域采用时谐分析的准静态电场控制方程:

式中:σ——体积电导率，S/m;

f——频率，Hz;

ε0——真空介电常数;

εr——相对介电常数;

U——电压，V。

主绝缘表面防晕层传导电场的控制方程为

式中:Us——防晕层上的电位，V;

σs——第i段防晕层的表面电导率，S/m;

n——边界上的法向向量;

J——电流密度，A/m。

表面电导率的选用是为了计算方便，与表面电阻率成倒数关系，同样具有非线性特性，表示为

式中:ρi——第i段防晕层的特征电阻率，Ω;

βi——第i段防晕层的非线性系数，m/V;

ET——防晕层表面的切向电场强度，V/m。

损耗密度

2.2 弱解形式推导

主绝缘表面防晕层区域，采用弱解形式描述其控制方程，与主绝缘边界条件耦合，可实现线棒端部电场的求解。同时，利用泛函定理，将防晕层电场的二阶非线性常微分控制方程转换为求其等效积分形式的极值问题，对方程进行分步积分，使连续性要求降低一阶，改善了非线性求解的收敛性。

等效弱形式的推导过程如下:

将式(2)两端乘以试函数ν，再求解域内积分，得

等式两边利用格林公式进行分步积分，有

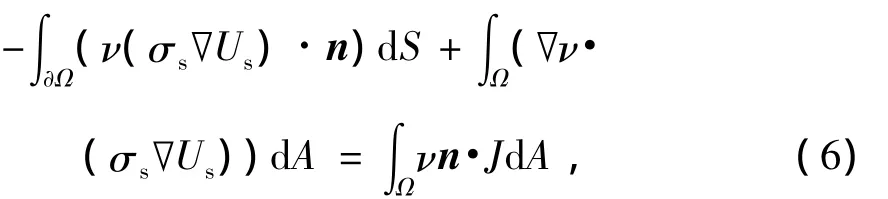
式中:∂Ω——积分边界;

Ω——积分区域。

根据式(6)整理得到弱解形式:

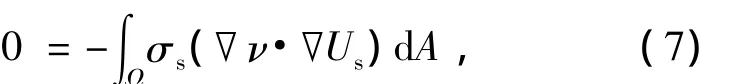
式(7)中▽ν为一阶微分算子，这就要求试函数ν应满足在Ω内连续。通过提高ν的连续性要求而降低求解变量Us的连续性要求，使求解变量的连续性要求被弱化了，所以这种方式被称为等效积分的“弱解”形式［8］。

3 计算结果与分析

采用COMSOL软件进行有限元计算，该软件具有多物理场耦合建模功能。网格使用默认剖分格式，产生12 934个三角形网格，将式(7)所推导的弱解形式作为防晕层弱解形式的边界条件，计算时选用非线性求解器。

3.1 防晕层电位分布

图2为定子线棒端部电位分布云图。由图2可以看出，从低阻层到高阻层，电压逐级增大，从高阻末端到引线，电压恢复到额定电压。中阻防晕层的电压由0增加到3.31 kV，中高阻防晕层的电压由3.31增加到17.69 kV，高阻防晕层的电压由17.69增加到27.92 kV。各段防晕层的非线性特性使得每段防晕层电压变化趋近直线，而且，表面电阻率越高，曲线斜率越大。

根据文献［4］编制的阻容链方法计算程序与文中结果(沿曲线a)比较见图3。图中曲线1为文中方法结果，曲线2为阻容链方法结果。首先明确电容器的概念。电容器是由绝缘电介质隔开的两块导体构成的器件。在电机定子线棒端部，主绝缘夹在导体铜排与半导体防晕层之间，防晕层电阻率越大，其容纳电荷的能力越弱，即等效电容越小。在传统阻容链方法中这种因素未予考虑，而有限元准静态方法则能充分考虑并精确计算。相同介电常数条件下，文中方法中的等效电容小于阻容链方法，而且，电阻率越高，电容越小，容抗越大，分压能力越强。所以，文中方法比阻容链方法的电位向后部集中。

图2 端部电位分布Fig.2 Distribute of electric potential of end-winding

图3 两种方法的电位分布比较Fig.3 Distribute of electric potential of end-winding of double method

3.2 防晕层电场强度分布

图4显示了防晕层切向电场强度分布云图。每段防晕层的电场强度从始端到终端是减小的。中阻层电场强度由0.62减小到0.47 kV/cm，中高阻防晕层的电场强度由1.63减小到1.00 kV/cm，高阻防晕层的电场强度由1.98减小到0.31 kV/cm。

图4 防晕层切向电场强度分布Fig.4 Distribute of tangential electric field of corona protective coating

文中方法(沿曲线a)的场强分布与阻容链方法对比见图5。由图5可见，两者的分布趋势较为一致。受非线性特性影响，各段防晕层场强分布均呈饱满的“三角”形态。受高阻末端至引线处表面电阻率为常数影响，高阻末端场强分布呈“尖顶”形态。文中方法防晕前段的分压能力弱于阻容链方法，致使防晕前部的场强减小，后部的场强增大。各段防晕层的非线性系数越大，这种变化越为明显。转角附近同一截面沿圆周方向的场强分布是存在差别的，这在损耗密度分布中有所体现。

图5 两种方法的电场强度分布Fig.5 Distribute of electric field of double method

3.3 防晕层损耗密度分布

由式(4)知，各段防晕层损耗密度与场强分布趋势一致，故最大值总是出现在各段防晕层的始端［9］。防晕层损耗密度云图见图6。使用透明效果加强显示，损耗密度分布(沿曲线b、c)对比见图7。由于转角内表面半径较小，转角内表面的损耗密度普遍大于外侧。中阻层转角外表面的损耗密度最大值出现在中间部位，为0.048 W/cm2，转角内表面最大值出现在内表面与窄边交接处，为0.065 W/cm2。中高阻层内、外表面最大值均在始端中部，分别为0.082和0.070 W/cm2。这种趋势与防晕实验中防晕层表面的发热状况一致。高阻层及高阻层末端由于表面电阻率很大，损耗密度较低。

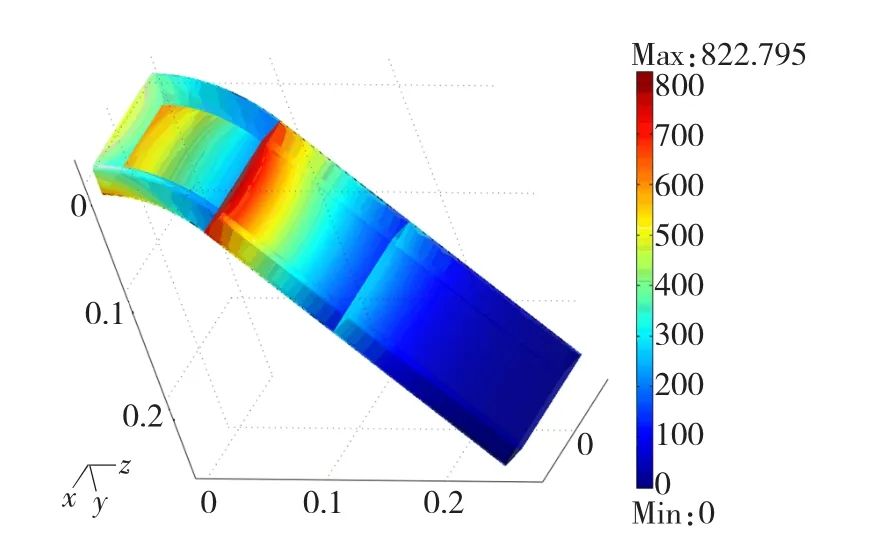
图6 防晕层表面损耗密度分布Fig.6 Distribute of surface loss density of corona protective coating

图7 不同位置沿圆周方向损耗密度分布Fig.7 Distribute of loss density at circumferential different position

两种方法(沿曲线a)的损耗密度分布对比见图8。两曲线的趋势依然一致，中高阻层始端最大，中阻层始端次之，高阻层始端最小。但阻容链方法计算结果误差很大，这是由于场强对损耗密度的影响更为显著。在防晕层优化计算中，多以损耗密度为重要的衡量手段，损耗密度减小意味着模型稳定性的增加，将有利于优化模型的运算。

图8 两种方法的损耗密度分布Fig.8 Distribute of loss density of double method

4 结论

(1)有限元弱解形式模型的建立，对于求解具有多段非线性防晕结构的三维定子线棒端部的电场分布，具有工程应用价值，可作为优化防晕层和主绝缘参数的理论依据，并为进一步建立优化计算模型提供基础。

(2)对于并非“纯电容”的线棒端部，文中计算方法能有效避免阻容链方法所引起的误差，更正电位、场强和损耗密度等参数的计算结果。

(3)非线性特性使防晕层表面的电位分布呈“直线”形态，各段防晕层场强分布均呈饱满的“三角”形态。与高阻层末端的搭接处，场强呈“尖顶”形态。

(4)各段防晕层表面场强与损耗密度的最大值均出现在始端，且转角内侧普遍大于外侧。对于防晕过转角结构，中阻层最大值出现在始端内表面与窄边交接处，中高阻层最大值出现在始端内表面中部。

(5)有限元弱解形式与多物理场建模相结合，为求解存在表面电阻率的三维电场分布提供方法，为不同维度求解区域的耦合仿真提供思路。

［1］刘 飞，金天雄，江平开，等.大型汽轮发电机主绝缘耐压和电老化试验中定子线棒端部防晕技术的研究［J］.大电机技术，2006(5):23－27.

［2］PHILIPS D B，OLSEN R G，PEDROW P D.Corona onset as a design optimization criterion for high voltage hardware［J］.IEEE Transactions on Dielectric and Electrical Insalation，2000(7): 744－751.

［3］MALAMUD R，CHEREMISOV I.Anticorona protection of the high voltage stator windings and semi-conductive materials for its realization［J］.IEEE International Symposium on Electrical Insulation，2000(7):32－35.

［4］刘上椿，李景富.多级碳化硅防晕层电场的数值计算——龙格－库塔法、牛顿法解多种介质中的二阶非线性常微分方程［J］.大电机技术，1981(3):29－34.

［5］刘瑛岩，徐传骧.大电机定子线圈端部SiC防晕层电场分布计算［J］.高电压技术，2002(1):15－16.

［6］BAKER A E，GULLY A M，WHEELER J C G.Finite element modelling of nonlinear stress grading materials for machine end windings［J］.International Conference on Power Electronics Machines and Drives，2002(CP487):265－268.

［7］欧阳鹏，王建辉，范成西，等.基于ElecNet的汽轮发电机定子绕组端部结构建模及电场计算［J］.大电机技术，2009(1): 14－18.

［8］胡建林，洪 川，杜 林，等.基于有限元弱解式的棒－板长空气间隙先导放电空间电场仿真研究［J］.中国电机工程学报，2008，28(10):148－154.

［9］刘上椿.20～26 kV高压电机定子线圈防晕结构优化设计［J］.大电机技术，1986(5):31－38.

Finite element calculation of electric field of large generator stator end-winding

SUN Yongxin，HU Chunxiu
(Harbin Institute of Large Electrical Machinery，Harbin 150040，China)

Aimed at addressing the vulnerability of anti-corona layer surface to the corona and thermal aging arising out of the uneven distribution of electric field on the large motor stator bar end，this paper describes the numerical calculation of distribution of electric field and loss density of large electric machine by combining the weak form of finite element method with the coupling modeling of multiphysics，and offers the comparison between the proposed method and RC-chain method.The study results show that such algorithm is capable of avoiding the algorithm error revealed by RC-chain method，thus increasing calculation accuracy，and it affords an effective solution to the problem encountered in modeling and defining boundary conditions by conventional finite element method，with a resultant improvement in the solution efficiency and accuracy.Anti-corona layer loss density computation gives the results consistent with heating conditions at corona test.The algorithm，capable of fulfilling the need of three-dimensional electric field calculation of stator end-winding with multi segmental non-linearity corona protective coating，provides not only the theoretical basis for calculating corona structure and material parameters，but also the basis for further designing the optimum calculation model.The algorithm features ideas for the finite element calculation of electric field with surface resistivity.

stator bar;corona protective coating;electric field calculation;nonlinear;weak form

TM85

A

1671－0118(2012)02－0182－05

2012－02－20

孙永鑫(1981－)，男，黑龙江省牡丹江人，工程师，硕士，研究方向:大电机绝缘技术应用及相关理论，E-mail:1981sunyx@ 163.com。

(编辑徐 岩)