锥度量空间中映象的一个新的公共不动点定理

史晓棠，谷 峰

（杭州师范大学理学院，浙江杭州 310036）

锥度量空间中映象的一个新的公共不动点定理

史晓棠，谷 峰

（杭州师范大学理学院，浙江杭州 310036）

自锥度量空间的概念被提出以来，已经有数位学者对其结构和性质进行了探讨和研究.该文通过构造新的映象类，建立并证明了锥度量空间中一对映象的公共不动点的存在性和唯一性，定理推广了黄和张［1］，Abbas和Jungck［2］以及宋，孙，赵和王［3］的主要结论.在该文中采用不同的迭代方法，获得了一些相关结论，这些结论可以用来讨论并阐述一些例子的实用性.

公共不动点；映射；锥度量空间

1 引言及预备知识

近年来，关于公共不动点理论及应用的研究受到越来越广泛的关注，取得了许多重要的研究成果.作为泛函分析的重要组成部分，非线性算子不动点的存在性和唯一性问题是非线性分析研究中的重要课题之一，并且广泛应用于微分方程和积分方程中.

最近，黄和张［1］用实数代替有序Banach空间定义了锥度量空间.他们证明了锥度量空间中的扩张映象的不动点定理，黄和张的结果进一步概括了Abbas和Jungck［2］的结论.

最近锥度量空间中映象的公共不动点的存在性在［1－7］中已被考虑.该文的目的是推广黄和张［1］，Abbas和Jungck［2］以及宋，孙，赵［3］的不动点定理.

同黄和张［1－5］，现在给出以下定义和结论.

定义1［1］设E是实Banach空间，如果P是E的子集，并且满足下面条件：

（i）P是非空的，闭的，并且P≠｛θ｝，

（ii）a，b∈R，a，b≥0，x，y∈P⇒ax＋by∈P，

（iii）x∈P，－x∈P⇒x＝θ，θ表示E中的零元素.则称P是E中一个锥.

给定E中一个锥P后，则定义半序：x≤y（x，y∈E），如果y－x∈P.若x≤y，x≠y，则记x＜y；若y－x∈intP（P的内部），则记x≪y.

锥P称为是正规的如果存在一个实数K＞0使得对所有的x，y∈E都有下式成立

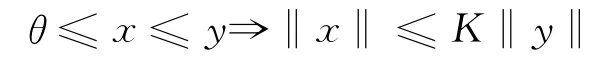
其中满足上式的最小正数K叫做P的正规常数.

锥P被称为是正则的如果每一个递增序列有上界且收敛，即：若｛xn｝是一个序列，且

对于y∈E，存在x∈E使得‖xn－x‖→θ，n→∞.等价的说，锥P是正则的当且仅当每一个递减序列有下界并且收敛.很显然，正则锥一定是正规锥.

下面假设E是一个实Banach空间，且P是E的子集，intP≠Φ，≤是定义在P上的偏序.

定义2［1－2］设X是非空集合，若映射d：X×X→E满足下列3个条件：

（i）d（x，y）≥θ，∀x，y∈X，而且d（x，y）＝θ当且仅当x＝y；

（ii）d（x，y）＝d（y，x），∀x，y∈X；

（iii）d（x，z）≤d（x，y）＋d（y，z），∀x，y，z∈X.

则称d是X上的一个锥度量，（X，d）称为锥度量空间.

定义3［2］令（X，d）是一个锥度量空间，那么｛xn｝称为是：

（i）柯西序列，如果∀c∈E且θ≪c，存在正整数N使得当n＞N时，有d（xn，x）≪c对所有n，m＞N都成立；

（ii）｛xn｝收敛于x∈X，如果对每一个θ≪c，存在一个自然数N使得d（xn，x）≪c对所有n＞N成立.

定义4［2］令f，g是X上的自映象，如果x∈X，有fx＝gx，那么x称为是f和g的重合点.

定义5［4］锥度量空间X上的两个自映象f和g称为是若相容的，如果它们在重合点处可交换，即，如果对x∈X，有fx＝gx⇒fgx＝gfx.

定义6令函数F：E→R＝｛u∈E｜u≥θ｝

（1）F被称为是单调的，当且仅当F是递增的，且u1≤u2时有F（u1）≤F（u2）；或者F是递减的，且u1≤u2时有F（u1）≥F（u2）；

（2）F被称为是连续的，当且仅当F（u）→F（u0）（u→u0）.

引理1［5］令（X，d）是一个锥度量空间，E是实Banach空间且锥P⊂E是非空的，令｛xn｝是X中的一个序列，有

（a）｛xn｝收敛到x∈E当且仅当d（xn，x）→θ，n→∞；

（b）｛xn｝是一个柯西序列当且仅当d（xn，xm）→θ，n，m→∞.

引理2［5］令（X，d）是一个锥度量空间，P是非空锥，｛xn｝是X中的序列.如果｛xn｝收敛到x并且｛xn｝也收敛到y，那么有x＝y.

注1比较引理1，引理2和［1］中的引理1，引理2，发现不要求P是正规锥.因此，引理1，引理2推广了［1］中引理1，引理2.

引理3［6］令（X，d）是一个锥度量空间，｛xn｝是X中的序列.如果存在常数h∈（0，1）满足

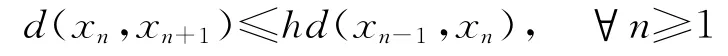
则｛xn｝是X中的一个柯西列.

引理4［2］令（X，d）是一个锥度量空间，P是正规锥，K是正规常数.如果映象f，g：X→X满足

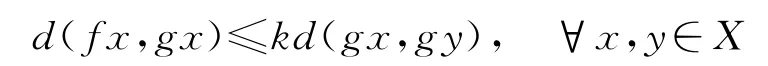
其中k∈（0，1）是一个常数.如果f（X）⊂g（X）且g（X）是X中完备的子集，那么f和g在X中有唯一的重合点.此外，如果f和g是弱相容的，那么f和g有唯一的公共不动点.

引理5［7］锥度量空间中收敛序列的极限是唯一的.

2 主要结果

在这一部分中，将给出锥度量空间中映象的公共不动点定理.

定理1设（X，d）为完备的锥度量空间，P是正则锥，令递减连续函数a（t）：E＋→（0，1）.假设映象f，g：X→X满足条件

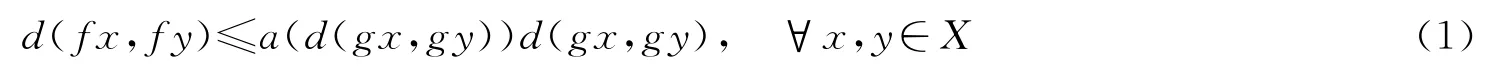
对所有的x，y∈X均成立.

如果f（X）⊂g（X）且g（X）是X中完备的子集，那么f和g在X中有唯一的重合点.此外，如果f和g是弱相容的，那么f和g有唯一的不动点.

证明令x0∈X是任意一点.因为f（X）⊂g（X），所以存在一点x1∈X使得fx0＝gx1.通过归纳总结，存在一个序列｛xn｝使得fxn＝gxn＋1（n＝0，1，2，3，…）.

因此，由（1）得，对任意自然数n，有

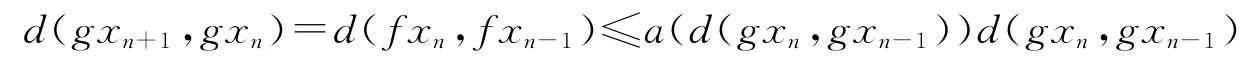
所以

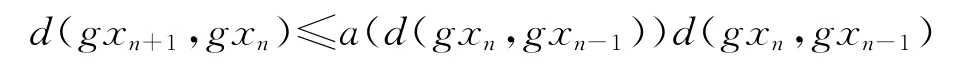
因为a（t）＜1，那么d（gxn，gxn＋1）是一个递减序列.假设序列d（gxn，gxn＋1）收敛到v∈X.现在证明v＝0，否则令v＞0，因为d（gxn，gxn＋1）≥v，则有

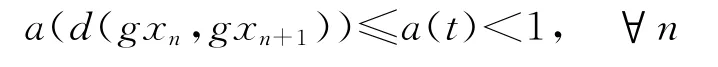
因此

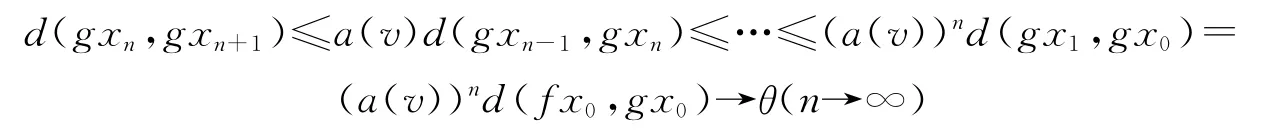
所以，v＝0.

由引理3，可以得到gxn是一个柯西序列.

因为｛g（xn）｝⊂g（X）且g（X）是完备的，则存在q∈q（X）使得gxn→q（n→∞），并且∃p∈X使得gp＝q.

因此，由（1），有

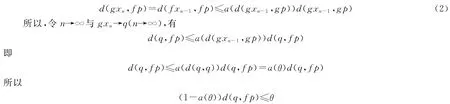
因此，由a（t）＜1，得到d（q，fp）＝θ，即fp＝q＝gp.

所以可以得到结论f和g有唯一的重合点.假设存在另一点u∈X使得fu＝gu.

因此，由（1），有

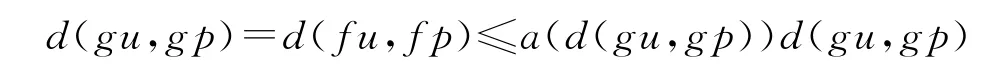
由以上以及a（t）＜1，很容易得到d（gu，gp）＝θ，即gu＝gp，所以u＝p.

由引理4，其余部分不难证明.

在定理1中，如果g＝IX是X上的恒等映象，并且X是完备的锥度量空间，那么，由定理1，可以立即得出以下结论.

推论1设（X，d）为完备的锥度量空间，P是正则锥，令递减连续函数a（t）：E＋→［0，1）.假设映象f：X→X满足条件

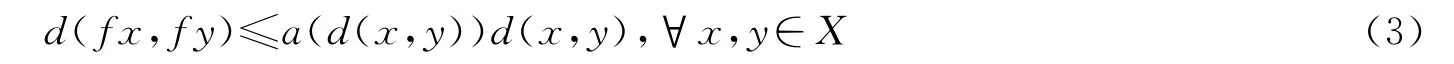
对所有的x，y∈X均成立.

那么f在X中有唯一的一个点x＊，使得对任意x0∈X，连续迭代

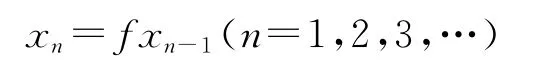
收敛到x＊.

定理2设（X，d）是一个锥度量空间，P是正则锥，令递减连续函数a（t），b（t），c（t）：E＋→［0，1）是常数并且a（t）＋b（t）＋c（t）＜1.假设映象f，g：X→X满足条件

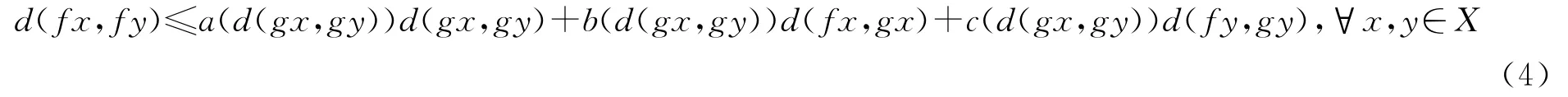
对所有的x，y∈X均成立.

如果f（X）⊂g（X）且g（X）是X中完备的子集，那么f和g在X中有唯一的重合点.此外，如果f和g是弱相容的，那么f和g有唯一的不动点.

证明令x0∈X是任意一点.因为f（X）⊂g（X），所以存在一点x1∈X使得fx0＝gx1.通过归纳总结，存在一个序列｛xn｝使得fxn＝gxn＋1（n＝0，1，2，3，…）.

因此，由（4）得，对任意自然数n，有

因为a（t）＋b（t）＋c（t）＜1，所以d（gxn，gxn＋1）是一个递减序列.假设d（gxn，gxn＋1）收敛到v∈X.现在证明v＝0，否则令v＞0，因为d（gxn，gxn＋1）≥v，则有

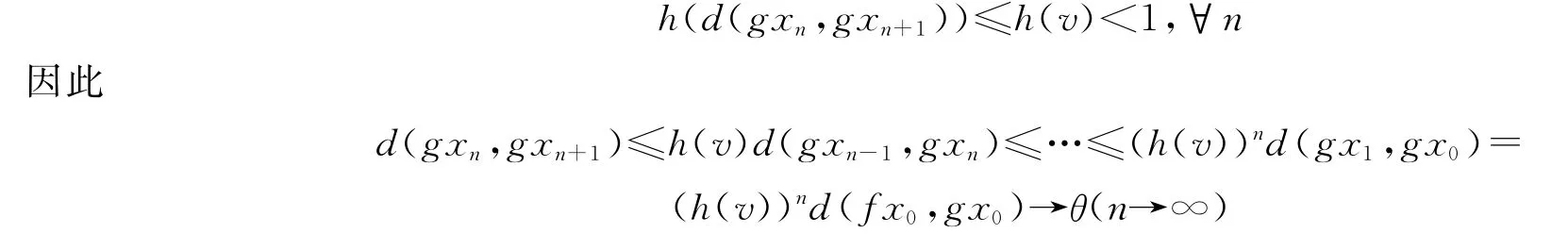
所以，v＝0.

由引理3，可以得到gxn是一个柯西序列.

因为｛g（xn）｝⊂g（X）且g（X）是完备的，则存在q∈q（X）使得gxn→q（n→∞），并且∃p∈X使得gp＝q.

因此，由（4），有

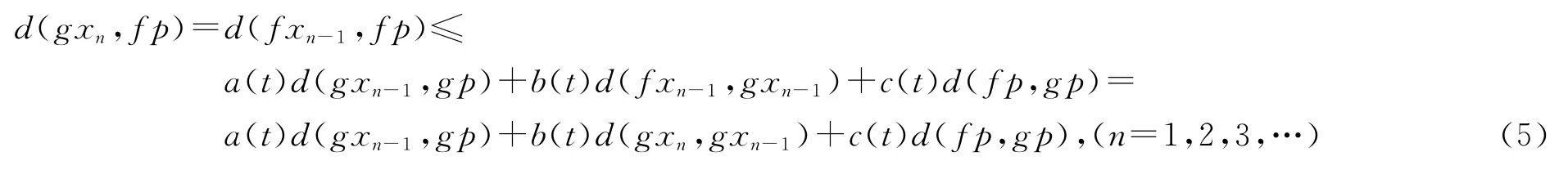
所以，令n→∞与gxn→q（n→∞），有

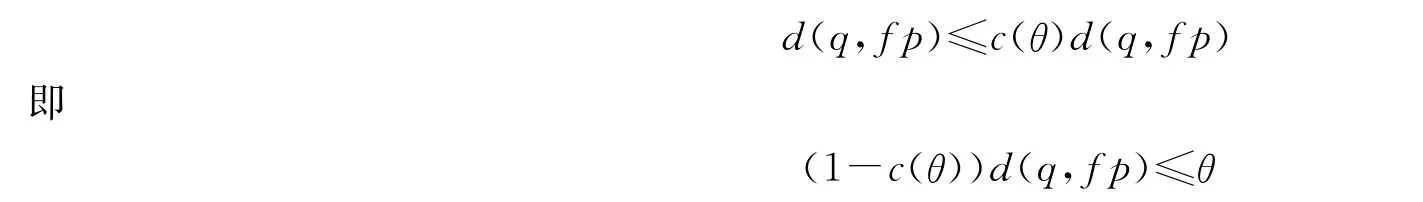
因此，由c（t）＜1，得到d（q，fp）＝θ，即fp＝q＝gp.

所以可以得到结论f和g有唯一的重合点.为此，假设存在另一点u∈X使得fu＝gu.

则由（4），有

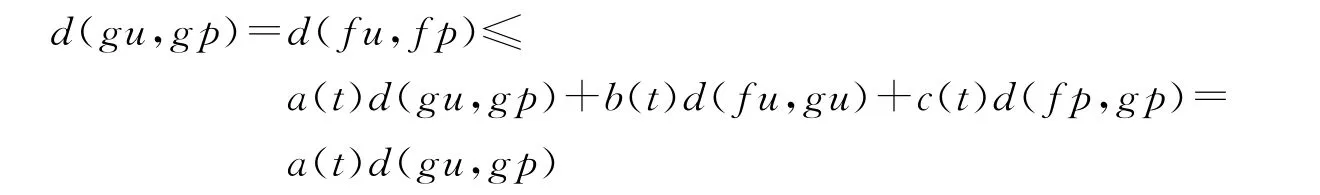
由以上以及a（t）＜1，很容易得到d（gu，gp）＝θ，即gu＝gp.

由引理4，其余部分不难证明.

定理2证毕.

在定理2中，如果g＝IX是X上的恒等映象，并且X是完备的锥度量空间，那么，由定理2，可以得出以下结论.

推论2设（X，d）是一个完备的锥度量空间，P是正则锥，令递减连续函数a（t），b（t），c（t）：E＋→［0，1）是常数并且a（t）＋b（t）＋c（t）＜1.假设映象f：X→X满足条件

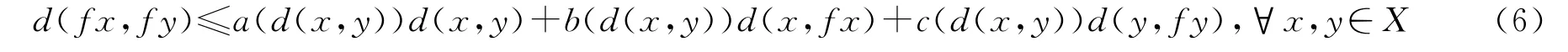
对所有的x，y∈X均成立.

那么f在X中有唯一的一个点x＊，使得对任意x0∈X，连续迭代

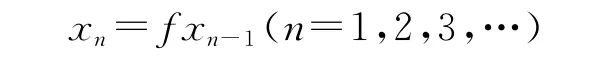
收敛到x＊.

定理3设（X，d）是一个锥度量空间，P是正则锥，令递减连续函数ai（t）：E＋→［0，1），（i＝1，2，3，4，5）是常数并且a1（t）＋a2（t）＋a3（t）＋a4（t）＋a5（t）＜1.假设映象f，g：X→X满足条件

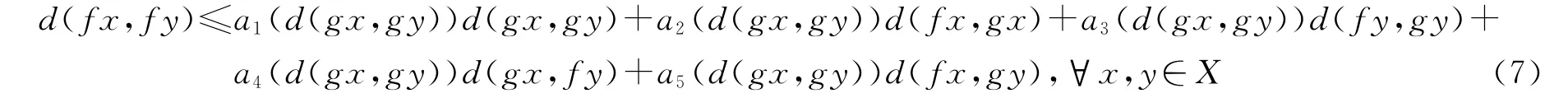
对所有的x，y∈X均成立.

如果f（X）⊂g（X）且g（X）是X中完备的子集，那么f和g在X中有唯一的重合点.此外，如果f和g是弱相容的，那么f和g有唯一的不动点.

证明令x0∈X是任意一点.因为f（X）⊂g（X），所以存在一点x1∈X使得fx0＝gx1.通过归纳总结，存在一个序列｛xn｝使得fxn＝gxn＋1（n＝0，1，2，3，…）.

因此，由（7）得，对任意自然数n，有

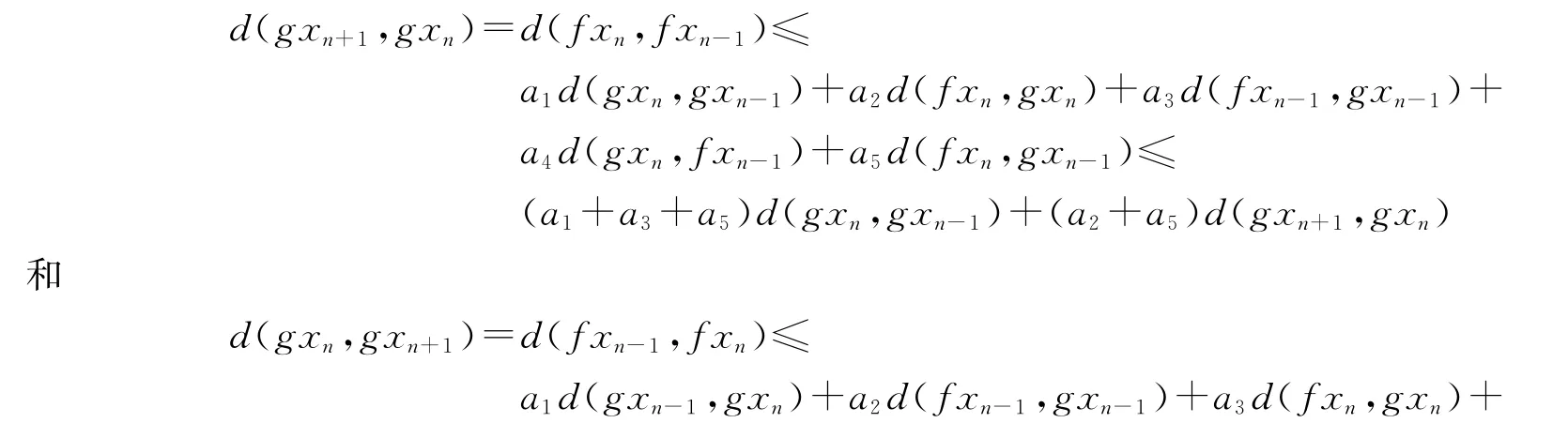
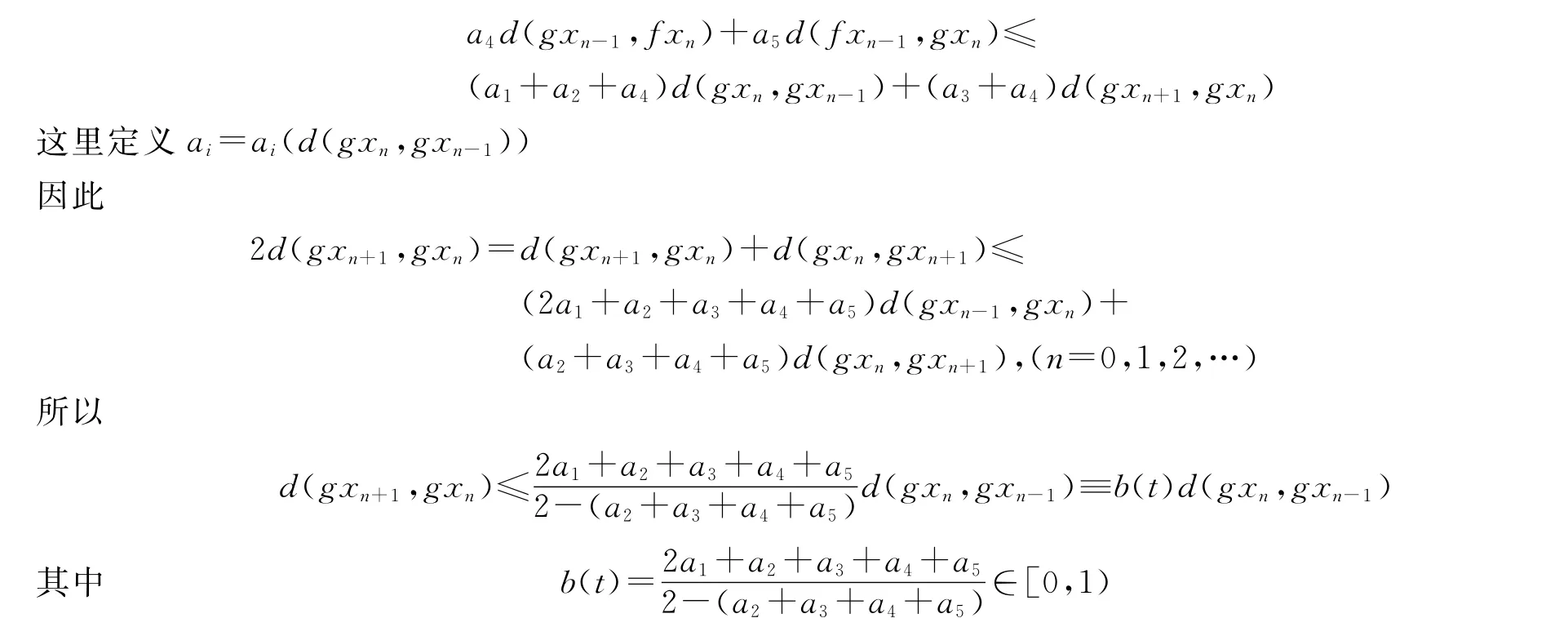
因为a1＋a2＋a3＋a4＋a5＜1，所以d（gxn，gxn＋1）是一个递减序列.假设d（gxn，gxn＋1）收敛到v∈X.现在证明v＝0，否则令v＞0，因为d（gxn，gxn＋1）≥v，则有

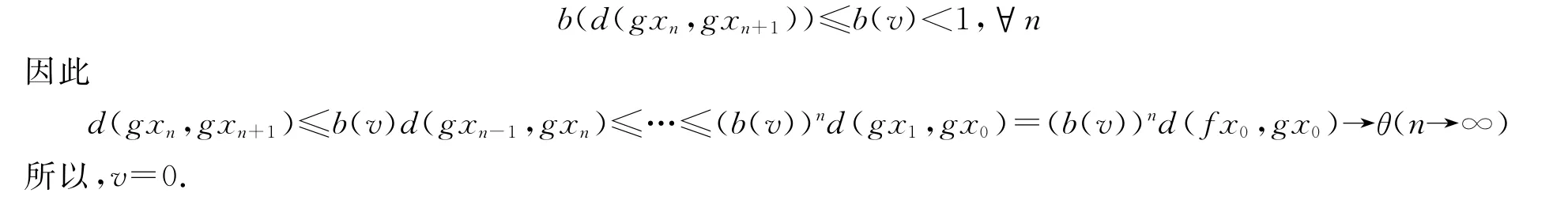
由引理3，可以得到gxn是一个柯西序列.

因为｛g（xn）｝⊂g（X）且g（X）是完备的，则存在q∈q（X）使得gxn→q（n→∞），并且∃p∈X使得gp＝q.

因此，由（7），有

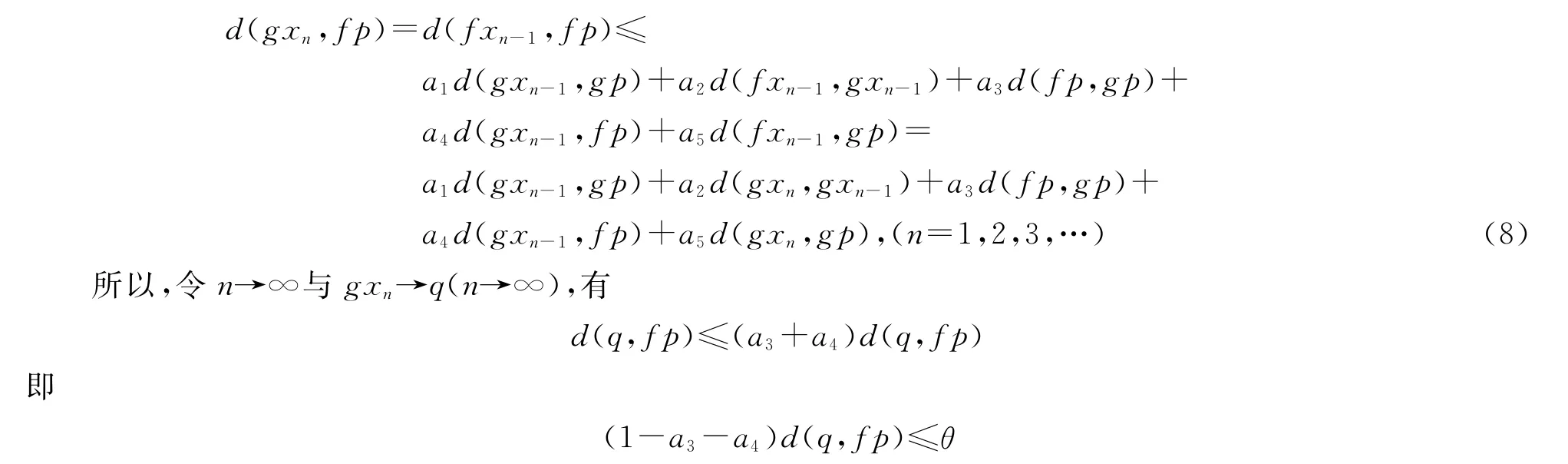
因此，由a1＋a2＋a3＋a4＋a5＜1，得到d（q，fp）＝θ，即fp＝q＝gp.

所以可以得到结论f和g有唯一的重合点.为此，假设存在另一点u∈X使得fu＝gu.则由（7），有

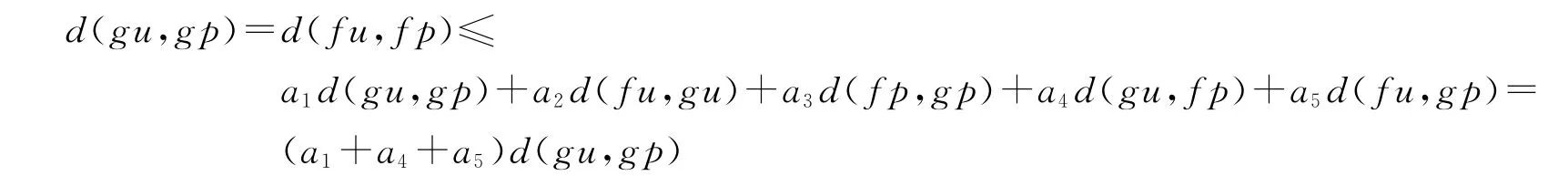
由以上以及a1＋a2＋a3＋a4＋a5＜1，很容易得到d（gu，gp）＝θ，即gu＝gp.

由引理4，其余部分不难证明.

定理3证毕.

注2很显然，［2］中的定理2.1是定理3中当a2＝a3＝a4＝a5＝0，a1＝k，g＝IX时的特例.

［2］中的定理2.3是定理3中当a1＝a4＝a5＝0，a2＝a3＝k，g＝IX时的特例.

［2］中的定理2.4是定理3中当a1＝a2＝a3＝0，a4＝a5＝k，g＝IX时的特例.

因此，定理3推广了［2］中Abbas和Jungck的主要结果.

在定理3中，如果g＝IX是X上的恒等映象，并且X是完备的锥度量空间，那么，由定理3，可以得出以下结论.

推论3设（X，d）是一个完备的锥度量空间，令递减连续函数ai（t）：E＋→［0，1），（i＝1，2，3，4，5）是常数并且a1＋a2＋a3＋a4＋a5＜1.假设映象f：X→X满足条件

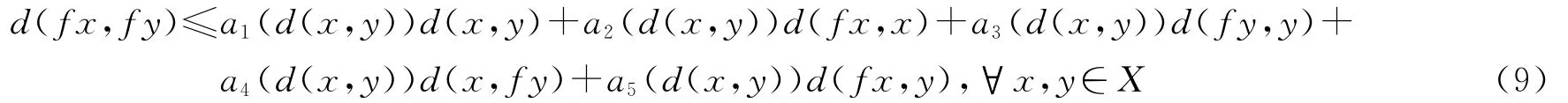
对所有的x，y∈X均成立.

那么f在X中有唯一的一个点x＊，使得对任意x0∈X，连续迭代

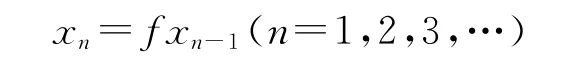
收敛到x＊.

注3很显然，［1］中的定理1是推论3中当a2＝a3＝a4＝a5＝0，a1＝k时的特例.

［1］中的定理3是推论3中当a1＝a4＝a5＝0，a2＝a3＝k时的特例.

［1］中的定理4是推论3中当a1＝a2＝a3＝0，a4＝a5＝k时的特例.

因此，推论3推广了黄和张的主要结果.

［1］Huang Longguang，Zhang Xian.Cone metric space and fixed point theorems of contractive mappings［J］.J Math Anal Appl，2007，332：1468－1476.

［2］Abbas M，Jungck G.Common fixed point results for noncommuting mappings without continuity in cone metric space［J］.J Math Anal Appl，2008，341：416－420.

［3］Song Guangxing，Sun Xiaoyan，Zhao Yan，etal.New common fixed point theorems for maps on cone metric spaces［J］.Applied Mathematics Letters，2010，23：1033－1037.

［4］Aamri M，EIMoutawakil D.Some new common fixed point theorems under strict contractive conditions［J］.J Math Anal Appl，2002，270：181－188.

［5］Rezapour S H，Derafshpour M，Hamlbarani R H.A review on topological properties of cone metric spaces［EB/OL］.（2008－02－07）［2011－02－01］.http：//atlas－conferences.com/c/a/w/q/04.htm.

［6］Yuan Qing，Qin Xiaolong.Fixed point theorems for generalized contractions in cone metric spaces［J］.International Journal of Modern Mathematics，2009，4（3）：269－275.

［7］Zhang Xian.Common fixed point theorem of Lipschitz type mappings in cone metric space［J］.Mathematics，2010，53（6）：1319－1148.

A New Common Fixed Point Theorem for the Mappings in Cone Metric Spaces

SHI Xiao－tang，GU Feng

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

Since the notion of cone metric spaces was raised，several authors have studied its constructions and properties.This paper established and proved the existence and uniqueness of a common fixed point for a pair of mappings in cone metric space by constrcting new mappings.The theorem generalized and unified the main results of Huang and Zhang［1］，Abbas and Jungck［2］as well as Song，Sun，Zhao and Wang［3］.This paper adopted different iterative methods and some related results are derived besides discussing illustrative examples which establish the utility of results proved in this paper.

common fixed point；mappings；cone metric space

O177 MSC2010：47H10；54H25

A

1674－232X（2012）02－0162－07

11.3969/j.issn.1674－232X.2012.02.014

2011－05－11

国家自然科学基金项目（11071169）；浙江省自然科学基金项目（Y6110287）；杭州师范大学研究生教改基金.

谷 峰（1960—），男，教授，主要从事非线性泛函分析及其应用研究.E－mail：gufeng99＠sohu.com