火灾下匀质防火保护钢构件温度计算（II）：实际火灾环境计算

张 超，李国强

（同济大学，上海，200092）

火灾下匀质防火保护钢构件温度计算（II）：实际火灾环境计算

张 超，李国强

（同济大学，上海，200092）

目前各国规范给出的计算火灾下有匀质防火保护的钢构件温度的公式都是基于标准火灾环境得到。标准火灾只包含升温段而实际火灾包括升温段和降温段。考察了将现有公式用于实际火灾环境计算的有效性。通过工况分析，考察了不同火灾、不同厚度、不同截面和不同防火涂料情形下的钢材温度。通过与有限元分析的结果比较，我国规范推荐的公式给出的钢材温度与有限元结果符合最好。研究同时表明欧洲规范中使用的避免升温早期负钢材温度增量的方法，即升温段当计算得到的钢材温度为负值时取增量为0，会引起最高钢材温度和降温段钢材温度的偏高，不适用于实际火灾环境计算。综合而言，我国规范最适用于实际火灾环境计算。

实际火灾；匀质防火保护；钢构件；温度计算；不同公式

0 引言

实际火灾一般会经历引燃、发展、“轰燃”、完全燃烧、衰减及熄灭六个阶段，如图1所示。“轰燃”是火灾由初始阶段的局部燃烧发展到全室燃烧的短暂过度阶段［1］。“轰燃”发生前，火灾局限在初始可燃物附近、烟气层稀薄、室内温度低，火灾容易扑灭、人员生还可能性大、结构受到的威胁小；“轰燃”发生后，室内所有可燃表面同时燃烧、火焰烟气充满室内，室内温度高，火灾很难扑灭、人员生还可能性极小、结构受到的威胁大。因此，研究中根据“轰燃”是否发生将火灾划分为“轰燃”前火灾和“轰燃”后火灾。对于通风条件良好且有足够可燃物的中小房间，发生的火灾将会经历“轰燃”，因此一般用“轰燃”后火灾模型模拟中小室火灾；而对于大空间或喷淋有效工作的房间，因为燃料的限制或喷淋的有效控火作用，发生的火灾一般不会经历“轰燃”，一般用“轰燃”前火灾模型或区域火灾模型模拟该类火灾。“轰燃”后火灾对结构安全最为不利，结构抗火研究和设计中通常考虑该类火灾。

图1 完整的室内火灾曲线示意图Fig.1 Illustration of a general compartment fire

实际火灾的行为复杂，受诸多因素影响，如房间内的主动控火、灭火措施（如喷淋系统）、火灾荷载密度及其分布，燃料燃烧性能、通风条件、房间尺寸和几何形状、及壁面材料的热工参数等［1］。截止目前，从简单到复杂，火灾行为可由经验公式（如标准火灾曲线和参数火灾曲线［2］）、区域模型（如模拟“轰燃”后火灾的单区域模型［3］和模拟“轰燃”前火灾的双区域模型［4］）、和CFD场模型（如火灾动力学模拟软件FDS［5］）模拟。

在基于性能的抗火设计方法中，需要合理确定火灾下钢构件的温度。在本论文的姊妹篇［6］中介绍了目前各国规范给出的计算火灾下匀质防火保护钢构件的温度的不同公式。这些公式在推导过程中使用的都是标准火灾环境，可能不适用于实际火灾计算。

本文考察了上述公式运用于实际火灾环境计算的有效性。研究中采用“瑞典”曲线和测得的火灾曲线代表实际火灾环境。考察了不同参数的影响，包括涂层厚度、截面系数和防火涂料类别。研究中，不同公式计算的结果与有限元结果进行了比较。通过比较研究，给出了用于实际火灾计算的相对最佳公式。

1 不同计算公式

在姊妹篇［6］中给出了现有的计算火灾下匀质防火保护钢构件温度的不同公式。出于论述完整性考虑，表1给出了所考察的计算公式及其表达式。

表1 火灾下匀质防火保护钢构件温度计算的不同公式Table 1 Different formulae for calculating the temperature of uniformly insulated steel members in fire

2 实际火灾曲线

图1中同时给出了标准升温曲线。与实际火灾曲线相比，标准升温曲线只包含上升段没有下降段。

图2至图5给出了所考察的实际火灾曲线。Pettersson等人［11］通过求解单区域火灾模型的热平衡方程给出的“瑞典”曲线在工程中引用较多，图2给出了所考察的5条“瑞典”曲线，图中标记为“sw1”到“sw5”。图3给出了英国建筑研究院（Building Research Establishment，简称BRE）在卡丁顿做的足尺火灾试验［12］中测得的8条室内平均温度曲线，图中标记为“test1”到“test8”。图4给出了著名的卡丁顿8层钢框架火灾试验［13］中测得的室内平均温度曲线，包括“大房间”火灾、“办公室”火灾和“角落”火灾。图5给出了Dalmarnock火灾试验［14］中测得的室内平均温度曲线。

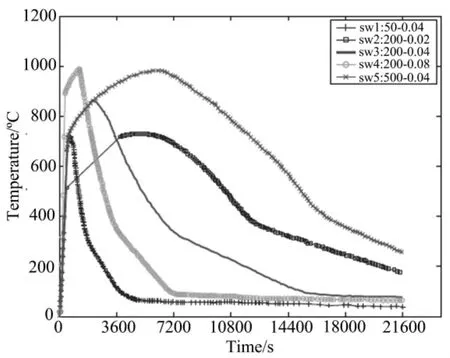
图2 考察的不同开口系数和火荷载下的“瑞典”火灾曲线（图中“50-0.04”表示开口系数为0.04m1／2，火荷载为50MJ／m2，其他类推）Fig.2 The investigated‘Swedish’fire curves for different opening factors and fire loads（e.g.50-0.04corresponds to opening factor of 0.04m1／2 and fire load of 50MJ／m2）

图3 卡丁顿BRE足尺火灾试验中测得的平均室内温度Fig.3 The measured average compartment temperature time curve in BRE full-scale test at Cardington

图4 卡丁顿8层钢框架火灾试验中测得的平均室内温度Fig.4 The recorded average atmosphere temperature time curves in Cardington 8story building fire tests

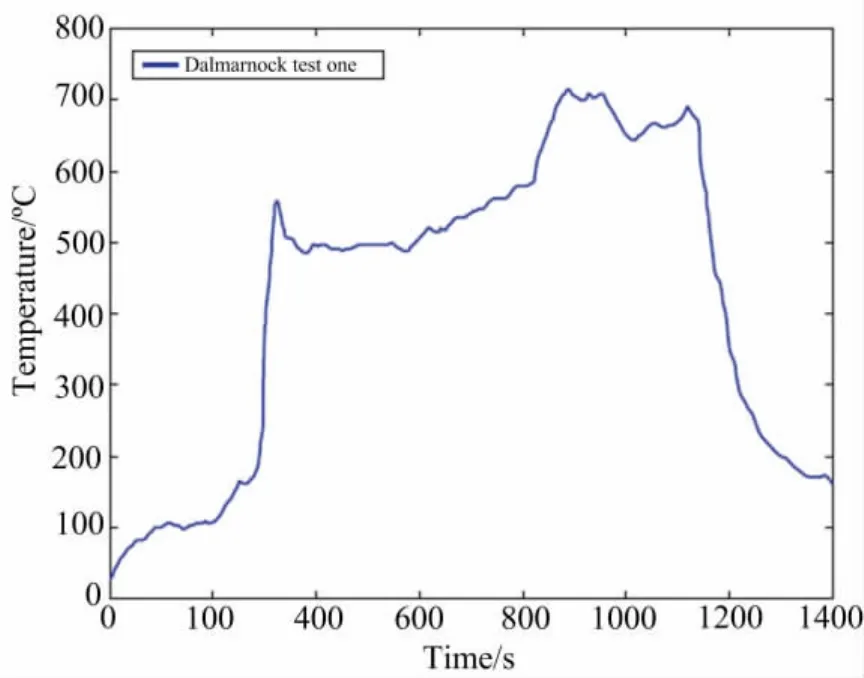
图5 Dalmarnock火灾试验中测得的平均室内温度曲线Fig.5 The measured average compartment temperature time curve in Dalmarnock fire test one

3 工况分析

3.1 不同火灾

考察上述实际火灾下有匀质防火保护的工字形钢截面的温度。截面为 H300×300×10×15，由30mm厚的普通防火涂料保护。涂料的导热率为0.12W／mK。经计算截面的形状系数为152m－1，加保护后的截面的耐火极限可达2小时。

图6给出了所考察的“瑞典”火灾下由不同公式计算得到的钢材温度的部分结果。图中也同时给出了有限元计算结果。整体而言，公式计算结果在升温段和降温段均与有限元结果符合良好。

图7给出了所考察的BRE火灾下由不同公式计算得到的钢材温度的部分结果。除了Pettersson公式，其他公式给出的结果在升温段和降温段均一致，且与有限元结果符合良好。Pettersson公式与其他公式在降温段符合较好，但在升温段相差较大。所有公式给出的最高钢材温度均与有限元分析的结果符合良好。

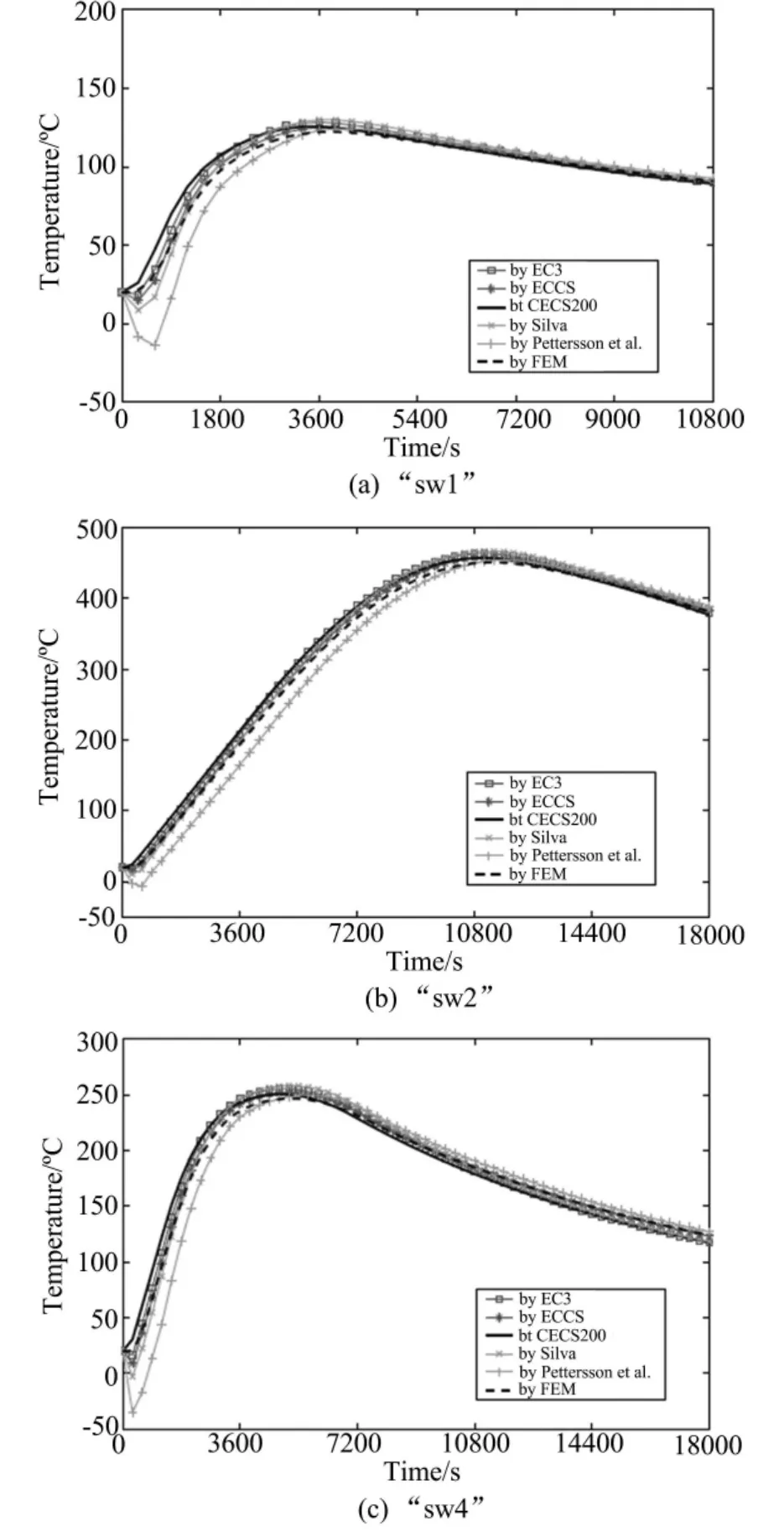
图6 “瑞典”火灾下不同方法得到的钢材温度的部分结果Fig.6 Some results of calculated steel temperatures by different formulae and FEM for“Swedish”fires

图8给出了所考察的卡丁顿8层框架火灾下由不同公式计算得到的钢材温度的部分结果。图中同时给出了测定的室内平均温度。公式结果与有限元结果符合良好。

图9给出了所考察的Dalmarnock火灾下由不同公式计算得到的钢材温度的部分结果。公式结果与有限元分析的结果符合较好。

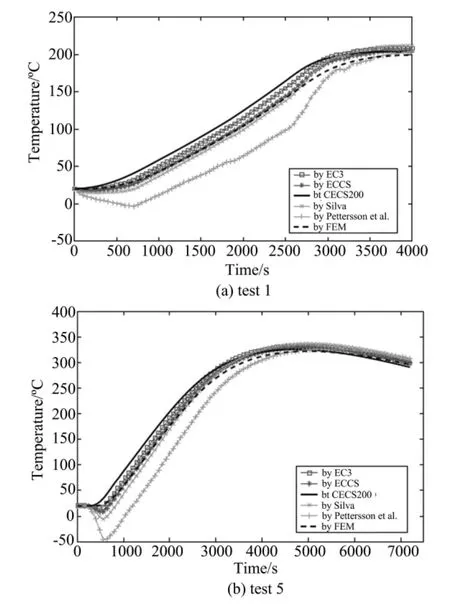
图7 BRE卡丁顿火灾下不同方法得到的钢材温度的部分结果Fig.7 Some results of calculated steel temperatures by different formulae and FEM for BRE Cardington fire tests

3.2 不同涂层厚度

考察上述钢截面的涂层厚度为13mm，30mm和48mm（对应的耐火极限为1小时，2小时和3小时），在“sw4”火灾下的温度。图10给出了计算得到的钢材温度结果。

3.3 不同截面

考察由30mm普通防火涂料保护的不同钢截面，H200×200×8×12，H300×300×10×15和H400×400×15×25（对应的截面系数为191m－1，152m－1和94m－1），在“sw4”火灾下的钢材温度。图11给出了计算得到的钢材温度结果。

3.4 不同防火涂料

考察了由30mm不同防火涂料保护的H300×300×10×15截面在“sw4”火灾下的钢材温度。除上面的普通防火涂料外，考察的另两种防火涂料为石膏板和普通混凝土。图12给出了计算得到的钢材温度结果。

对于由30mm石膏板保护的情形，不同公式给出的结果在降温段与有限元分析的结果符合较好。我国公式和欧钢协公式给出的钢材最高温度较好，其他公式给出的最高温度偏高。除我国公式外，其他公式给出的结果在升温段均偏低很多。

在图12b中同时也给出了在受火表面利用狄利克雷（Dirichlet）边界条件和诺依曼（Neumann）边界条件计算得到的有限元分析的结果。与诺依曼边界有限元结果相比，公式给出的结果均不理想；与狄利克雷边界有限元结果相比，我国规范给出的钢材温度符合较好。在降温段，基于狄利克雷边界得到的欧洲规范和巴西规范公式计算的钢材温度与狄利克雷边界有限元分析的结果符合较好。

图8 卡丁顿框架火灾下不同方法得到的钢材温度的部分结果Fig.8 Some results of calculated steel temperatures by different formulae and FEM for Cardington 8story fires

4 结果与讨论

对所考察的实际火灾，不同公式计算得到的最高钢材温度和降温段的钢材温度与有限元分析的结果符合良好，如图6－图9所示。除Pettersson公式外，其他公式给出的升温段钢材温度与有限元结果符合良好。Pettersson公式在升温段给出的钢材温度可能偏低很多。

图9 Dalmarnock火灾下不同方法得到的钢材温度的部分结果Fig.9 Some results of calculated steel temperatures by different formulae and FEM for Dalmarnock fire

在所考察的不同涂层厚度、不同截面系数的工况中也得到上述结论，如图10和图11所示。

图10 “sw4”火灾下不同防火涂层厚度时的钢材温度Fig.10 Predicted steel temperatures of section with different insulation exposed to“sw4”fire

对由石膏板和普通混凝土保护的钢构件，除我国公式外其他公式在早期升温段给出的的温度均偏低很多，如图12所示。对于密度高、导热率大的厚型防火涂料如普通混凝土，采用狄利克雷边界条件求解将使得升温段的钢材温度偏高、降温段的温度降低，如图12b。

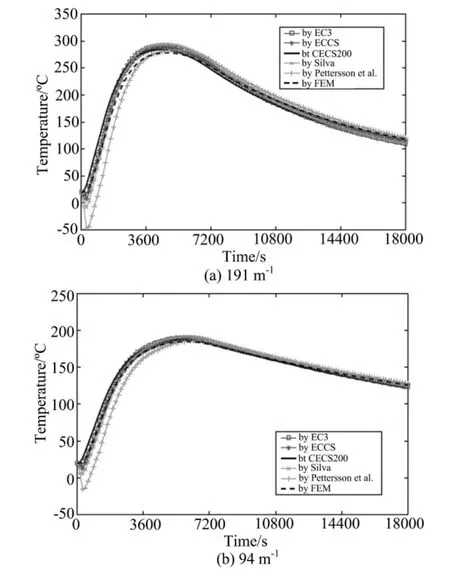
图11 不同截面系数时算的钢材温度Fig.11 Predicted steel temperatures with different section factor

在升温过程中，由欧洲规范、欧钢协、巴西规范和Pettersson公式计算得到的钢材温度增量可能为负值，如图8所示。在欧洲规范中为避免上述情况发生，当火灾增量为正值时，若计算得到的钢材温度增量为负值则取钢材增量为0。这样处理对于标准火灾环境下的计算可以［6］，但对于实际火灾环境下的计算，该处理可能引起最高钢材温度和降温段的钢材温度偏高很多，如图13所示。

5 结论

目前各国规范给出的计算火灾下有匀质防火保护的钢构件温度的公式均是基于标准火灾得到，本文考察了将现有公式用于实际火灾计算的可行性。本文的主要结论如下：

（1）整体而言，各国规范公式给出的最高钢材温度和降温段的钢材温度结果与有限元分析的结果符合良好。相较其他公式，无论是升温段还是降温段我国公式给出的结果均与有限元结果最为接近。

（2）除我国公式外，所考察的其他公式在升温初期给出的钢材温度均偏低。升温过程中除我国公式外的其他公式计算给出的钢材温度增量可能为负值。在欧洲规范中，升温过程中，当计算得到的钢材温度增量为负值时取增量为0，这种处理不适用于实际火灾环境计算，因为会使得最高钢材温度和降温段钢材温度偏高。

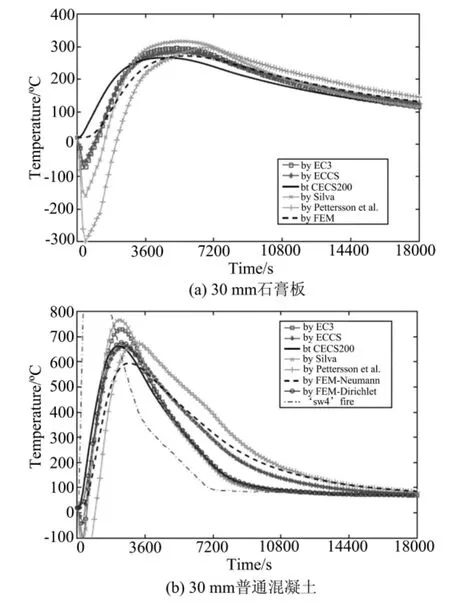
图12 “sw4”火灾下不同防火涂料保护的H300×300×10×15截面的钢材温度结果Fig.12 Predicted steel temperatures of H300×300×10×15 section protected by different fire proofing materials

（3）经比较，实际火灾下我国公式给出的钢材温度结果最好，因此实际火灾环境中推荐使用我国公式进行计算。

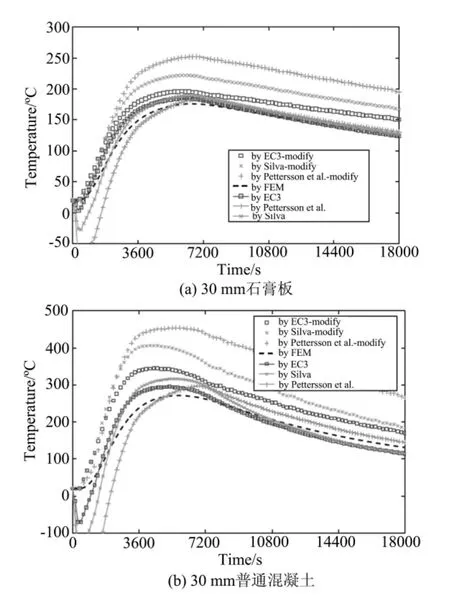
图13 取计算得到的钢材温度增量为0对计算结果的影响（“-modify”表示采用上述处理后的计算结果）Fig.13 Results of steel temperatures with and without taking the calculated positive steel temperature increment as zero

［1］Drysdale D.An introduction to fire dynamics［M］，Second edition.John Wiley and Sons，1999.

［2］EC1-1-2.Eurocode 1：Actions on sttructures-Part 1-2：General actions-Actions on structures exposed to fire［S］.British Standards Institution（BSI），2002.

［3］Babrauskas V.COMPF2：aprogram for claculating post-flashover fire temperatures ［R］.NBS Technical Note 991，National Bureau of Standards，1979.

［4］Cadorin JF，Franssen JM.A tool to design steel elements submitted to compartment fires-OZone V2.Part 1：pre-and post-flashover compartment fire model［J］，Fire Safety Journal，2003，38（5）：395-427.

［5］McGrattan K，McDermott R，Hostikka S，Floyd J.Fire Dynamics Simulator（Version 5）User’s Guide ［R］.NIST Special Publication 1019-5，National Institute of Standards and Technology（NIST），2010.

［6］李国强，张超.火灾下匀质防火保护钢构件温度计算（I）：理论与公式［J］.火灾科学，2012.21（2）：58-64.

［7］EN 1993-1-2.Eurocode 3：Design of steel structures-Part 1-2：General rules -Structural fire design［S］.British Standard Institution.London，2005.

［8］CECS 200：2006建筑钢结构防火技术规范［S］.

［9］Valdir Pignatta e Silva.Determination of the steel fire protection material thickness by an analytical process-a simple derivation［J］.Engineering Structures，2005，27：2036-2043.

［10］ECCS Technical Committee 3.European recommendations for the fire safety of steel structures［S］.Amsterdam：Elsevier Scientific Publishing Company；1983.

［11］O Pettersson，S Magnussen，J Thor.Fire engineering design of steel structures［M］.Stockholm：Swedish Institute of Steel Construction，1976.

［12］Lennon T，Moore D.The natural fire safety conceptfull-scale tests at Cardington［J］.Fire Safety Journal，2003，38（7）：623-643

［13］GM Newman，JT Robinson，CG Bailey.Fire safety design：a new approach to multi-story steel-framed buildings［M］，Second edition.SCI publication P288，2006.

［14］Abecassis-Empis C，Reszka P，Steinhaus T，Cowlard A.Characterisation of Dalmarnock fire Test One［J］.Experimental Thermal and Fluid Science，2008，32（7）：1334-1343.

Temperature calculation of uniformly insulated steel members in fire（II）：use in real fires

ZHANG Chao，LI Guo-qiang

（Tongji University，Shanghai 200092，China）

The formulae recommended by codes in different countries are originally derived in the standard fire which only includes heating phases，however，real fires have both heating and cooling phases.This paper investigates the applicability of the current formulae for calculation in real fires.Case studies are conducted to investigate the parameters for different real fires，different insulation thicknesses，different sections and different fire proofing materials.Comparing with FEM results，the formulae recommended in Chinese code give good predictions.The study also shows that the treatment adopted by eurocode to avoid negative steel temperature increment in early heating phase，for which if the calculated steel temperature increment is negative then the increment is taken as zero，is not suitable for real fires，because it will lead to over-predictions of the maximum steel temperature and steel temperatures in cooling phases.Overall，the formulae given in Chinese code are recommended for calculation in real fires.

Real fire；Uniformly insulated steel members；Steel member；Temperature calculation；Different formulae

TU375.4；X932

A

1004-5309（2012）-0058-07

10.3969／j.issn.1004-5309.2012.02.02

2011-11-30；修改日期：2011-12-29

张 超（1984-），男，湖北湛江人，工学博士，主要从事纲结构抗火。