建筑大空间火灾模拟及升温计算简单公式

张 超，李国强

（同济大学，上海，200092）

建筑大空间火灾模拟及升温计算简单公式

张 超，李国强

（同济大学，上海，200092）

钢结构经常用于建筑大空间环境。因为使用和功能要求，建筑大空间内通常无法设置防火墙来阻止火灾的水平传播，而是通过设置燃烧岛、防火舱及防火隔离带等措施将可燃物限制在一定区域内。大空间内可能的火灾为区域火灾。给出了模拟大空间火灾的理论模型和升温计算简单公式。公式基于火羽流相关理论，并引入工程相关常数得到。通过工况分析，考察了两种不同火灾场景，公式的计算结果与场模拟软件FDS结果进行了比较，二者符合良好。所给出的公式形式简单，式中参数的物理意义明确，推荐用于实际工程计算。

建筑大空间；火灾；温度计算；简单公式；火灾动力学模拟

0 引言

建筑大空间因使用和功能要求通常无法设置防火墙来阻止火灾的水平传播。性能化消防设计中一般通过控制使用过程中的可燃物，并设置燃烧岛、防火舱及防火隔离带等措施来限制大空间内的火灾规模和火灾的水平传播［1］。基于以上措施，大空间火灾通常不会发生“轰燃”，而是局限在初始火源附近，为区域火灾［2］。

目前各国结构抗火设计规范中给出的火灾下构件的升温计算公式均是针对发生“轰燃”后的一般室内火灾提出的［3，4］。因为“轰燃”作用，室内火灾环境将趋于空间均匀分布，因此可以用单一的温度时间曲线（如标准火灾升温曲线）来代表火灾环境，并用简单的一维传热模型来计算（钢）构件的升温［3］。但在区域火灾中火灾环境（如气体温度）空间分布不均，传热过程（主要是辐射传热）复杂，相应的受火灾影响的构件的升温计算也比较困难，目前各国规范均未给出合适的计算公式［5，6］。

合理模拟大空间火灾是进行大空间抗火设计的基础。研究中，常采用经验公式［5］，双区域模型［7］和场模型［8］来模拟大空间火灾。双区域模型将室内划分为上部热烟气区和下部冷空气区，并假定不同区域内的质量、温度均匀分布，引进相关简化假定后，通过求解不同区域内的热平衡方程和质量守恒方程可得到区域内气体的平均升温［9］。区域模型计算得到的烟气平均温度一般很低，而实际大空间火灾中火源附近温度很高、对结构安全威胁较大。因此，区域模型因为不能考虑烟气层内的温度梯度不适合用于大空间抗火设计。场模型能考虑火灾环境中的真实温度分布，但场模型的计算非常复杂，不便于工程运用。文献［10，11］根据数值模拟结果拟合给出了大空间火灾升温计算的简化公式，被我国钢结构抗火规CECS200采用。该式用统一的表达式来计算大空间火灾升温，虽然可以通过查表方式确定相关参数，但表格提供的数据有限，且表达式中相关参数的物理意义并不明确，不便于工程使用。

本文给出了计算建筑大空间火灾升温的简单公式。该公式以经典羽流理论模型为基础，能考虑大空间火灾中的温度梯度，表达式简单且物理意义明确。简单公式的有效性通过场模型验证。

1 火灾的热释放速率及火灾持续时间

大空间火灾为燃料控制性火灾，其热释放速率（Heat Release Rate，简称HRR）可通过以下三种方法确定：

（1）采用锤形量热仪实验测量。例如在性能化消防设计中将交通站房大空间中的书报亭设置为燃烧岛，通过实验测定书报亭火灾释放的热量［12］；

（2）通过叠加原理确定。目前，不同物体（如座椅、沙发、行李箱、显示器等）燃烧的HRR在相关燃烧手册中均可以查到，如文献［13］。大空间中，当潜在火源的组成较简单时（如座椅火灾、行李火灾等），可参考相关燃烧手册近似采用叠加方法确定可能火灾的HRR。

（3）由经验模型确定。根据可能火源面积Af、火灾荷载密度qf，d和自然火灾模型（Natural Fire Safety Concept，简称NFSC）确定。本方法被欧洲规范EC1［5］采用。以下介绍该方法。

如图1所示，NFSC假定火灾包括三个阶段，即发展阶段、稳态燃烧和衰减阶段。发展阶段的HRR由t2火模拟；当t2火计算得到的HRR达到给定的最大值HRRmax时，火灾进入稳态燃烧阶段；当设计火灾荷载的70%被消耗时，火灾进入衰减，衰减阶段的HRR线性递减。

发展阶段持续的时间为：

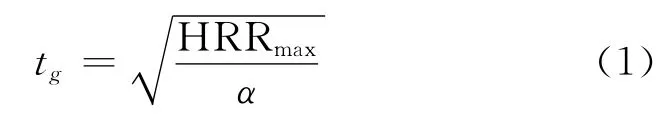
式中，α是根据火灾类型确定的火灾发展系数。

稳态阶段持续的时间由下式确定：

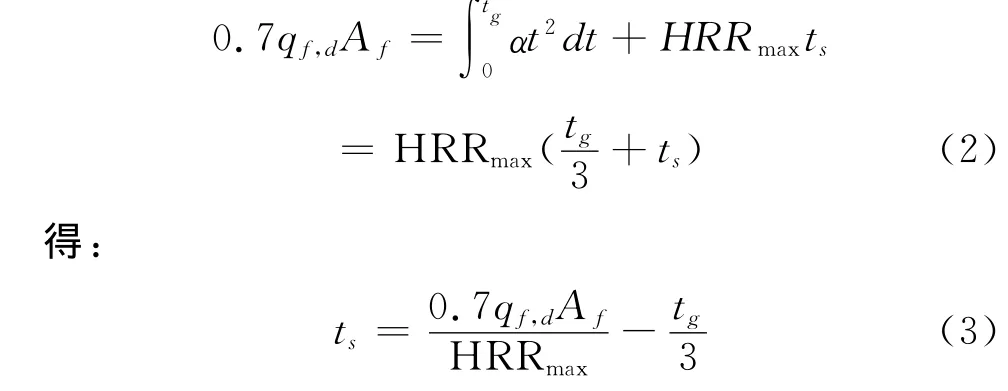
衰减阶段的持续时间由下式确定：

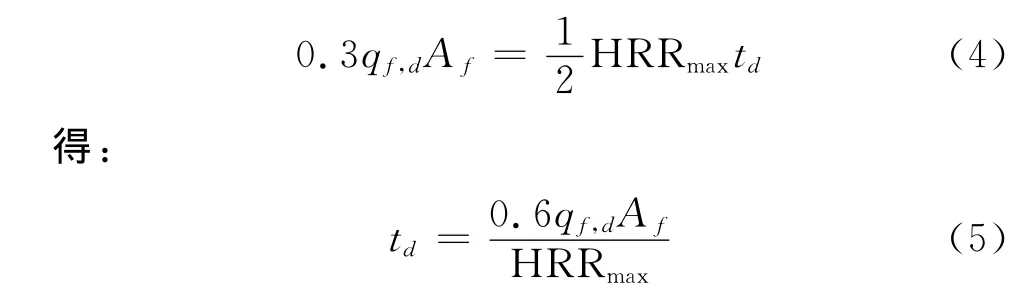
由热释放速率定义的火灾的持续时间为：

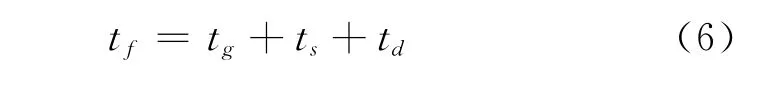
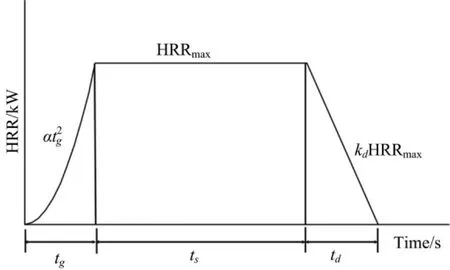
图1 自然火灾模型的热释放速率Fig.1 HRR history of a NFSC fire

图2 大空间火灾模型Fig.2 Illustration of large space fire model

2 大空间火灾模型及升温计算公式

建筑大空间因火灾荷载较少，体量大且通常设有排烟措施（如天窗），一般不会在顶棚下形成较厚的烟气层。图2给出了大空间火灾模型。火灾区域可划分为三个区域，即火焰区、羽流区和顶棚射流区。羽流通常指火焰上方因浮力而上升的烟柱［14］。羽流上升撞击顶棚后，向水平方向运动形成顶棚射流。

2.1 羽流温度

假设羽流为由一虚拟点火源产生、仅受浮力作用而上升的理想气体，并假定平面内羽流的速度和温度的分布形状，经典羽流理论由质量、动量和热平衡方程推导给出了羽流升温的理论公式。其中，通过假定平面内羽流的速度和质量均匀分布，即盖帽模型（top-hat）［15］，推导给出的羽流平均升温公式被广泛运用于防排烟计算，如美国规范NFPA 92B和英国规范TM 119及我国规范GB50016。

然而，羽流在平面内的温度分布并不均匀，一般认为平面内羽流温度的分布形状为正态分布形状［14，15］，即：

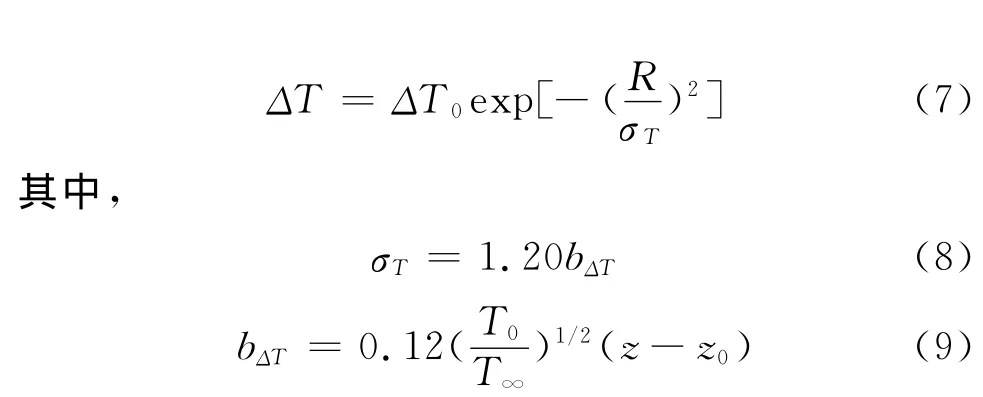
式中，ΔT、ΔT0表示温升。其中T0为中央羽流温度，由 Heskestad［15］给出的公式计算，为：

T∞为环境温度，cp、ρ∞为标准大气压下气体的比热和密度，g为重力加速度。带入相关气体常数后，式（10）变为欧洲规范EC1［5］采用的形式，即：

T0＝20＋0.25（1000˙Qc）2／3（z－z0）－5／3（11）式中，˙Qc＝ （1－χr）˙Q 是火灾热释放速率中的对流部分，χr是考虑热辐射损失的系数，˙Q为火灾热释放速率；z0是虚拟火源高度，可由Heskestad给出的公式计算［15］：

2.2 火焰温度

式（10）给出的羽流温度计算公式不适用于火焰区。火焰区的温度可由 Quintiere and Grove［16］给出的公式计算：

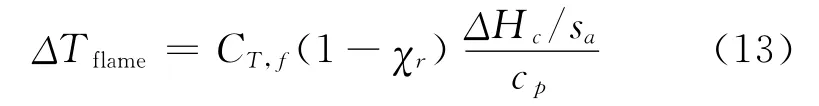
式中，CT，f是根据实验数据拟合得到的常数，通常取0.50［17］；ΔHc／sa是燃烧反应消耗单位质量空气释放的能量，对大量燃料的实验数据进行统计知ΔHc／sa＝3.03±0.02kJ／g［18］；cp是气体比热，通常取1.00J／gK。则式（13）可（保守）近似为：

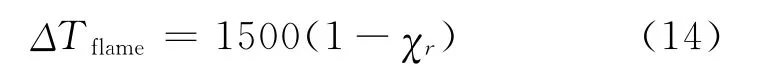
式（13）或式（14）认为进入火焰区的空气正好与燃料蒸气完全反应。实际随高度的增加，进入火焰区的空气量将大于反应所需的空气量。多余的空气将降低火焰区温度。

火焰区与羽流区一般根据火焰高度划分。Heskestad给出的火焰高度计算公式被EC1采用［15］，为：

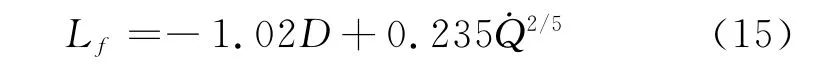
2.3 顶棚射流温度

Alpert［19］给出的顶棚射流最高温度（贴近顶棚处温度最高）计算公式被广泛用于设计感烟探测器的布置，为：

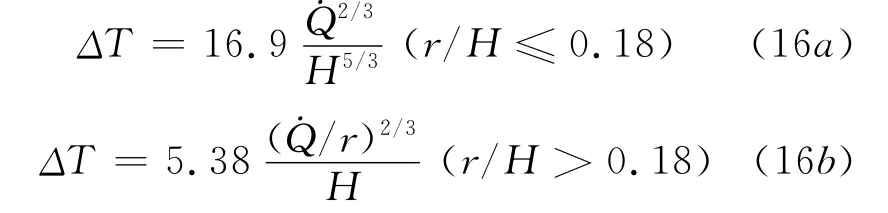
式（16）仅适用于计算火焰高度小于顶棚高度的弱羽流情形，对于火焰高度与顶棚高度相当的强羽流情形，应改用 Heskestad ＆ Hammada［20］给出的公式计算，为：

式中，ΔTp是顶棚高度处中央羽流的温升，可由式（2）或式（16a）计算；b是撞击区顶棚射流的名义半径，为：

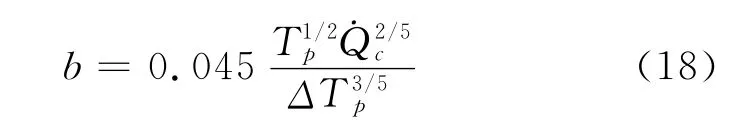
式（18）适用于自由火焰长度（由式（15）计算）与顶棚高度之比在0.3～3.0范围取值的情形。

3 大空间火灾的数值模拟

3.1 模拟工具

场模型可模拟火灾的真实温度分布。FDS（全称为“Fire Dynamic Simulator”）是当前火灾模拟中使用最多，最有效的场模拟软件。FDS采用大窝模拟（Large Eddy Simulation，简称LES）求解流体运动的Navier-Stokes方程；燃烧模型采用混合燃烧模型 （mixture fraction concept）；热辐射通过有限体积法（Finite Volume Method）求解特定波谱的灰体辐射传播方程计算；FDS中的固体传热模型为一维热传导模型。关于FDS的详细介绍可参见文献［8］。本文研究中采用FDS模拟大空间火灾的真实升温。在之前的研究中［21，22］，FDS有效的模拟了区域火灾试验中的热作用。

3.2 分析工况

工况一：楼面面积为10m×10m＝100m2，房间高度为5m。火灾场景拟用于考虑大空间中书报亭、小店铺等火灾。火源参照文献［23］取边长为2m的正方形池火，HRR＝1.6MW，为400s稳态火。

工况二：楼面面积为30m×30m＝900m2，房间高度5m。火灾场景拟用于考虑大空间中商业区域火灾。火源取边长10m的正方形火源。火灾的HRR和持续时间根据自然火灾模型确定，其中火灾荷载密度参照欧洲规范EC1中商业中心取qf，d＝600MJ／m2，单位面积热释放速率的最大值取HRRPUAmax＝250kW／m2。通过计算得火灾的持续时间为1小时。

3.3 数值模型

CFD模型的模拟结果受网格尺寸影响很大。FDS模拟时一般通过限制参数R＊的大小来保证模拟结果的精度。参数R＊定义为：

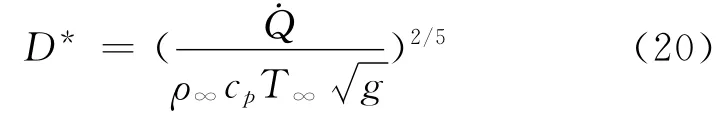
FDS使用手册［8］推荐的参数R＊的取值范围为1／4～1／16。工程中，通常认为R＊＝1／10能有效的模拟烟气的行为［17］。笔者之前的研究表明［21，22］，要有效模拟火焰区的行为，需要R＊＝1／20，当R＊＞1／20时模拟的火焰温度偏低。

在本文研究中，网格尺寸对FDS模拟结果的影响在工况一的模拟中进行了考虑。工况一的模拟中，使用了粗细两种网格尺寸，对应的R＊分别为1／10和1／20，其中细网格通过加密火源附近的网格实现，如图3所示。

式中，δx是网格尺寸；D＊为火灾特征尺寸，定义为：

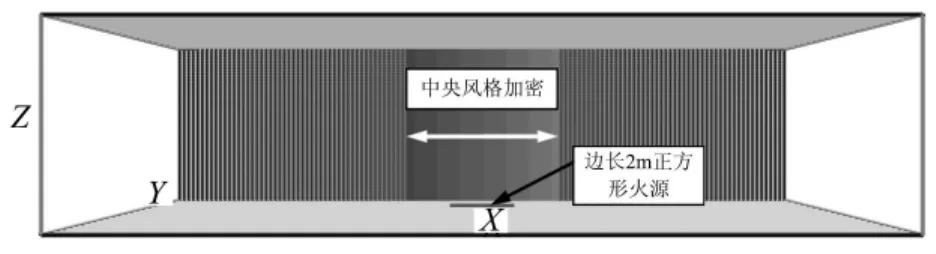
图3 工况分析中的数值模型（火源区域局部网格加密）Fig.3 Numerical model used in case studies（the grid size near the fire source has been refined）

4 结果与讨论

4.1 结果

图4给出了工况一中FDS模拟得到的火场温度分布的三维云图。图5给出了工况一中FDS模拟得到的火源中心面内的温度分布图。从图4和图5可知，大空间火灾中火场内温度空间分布不均。

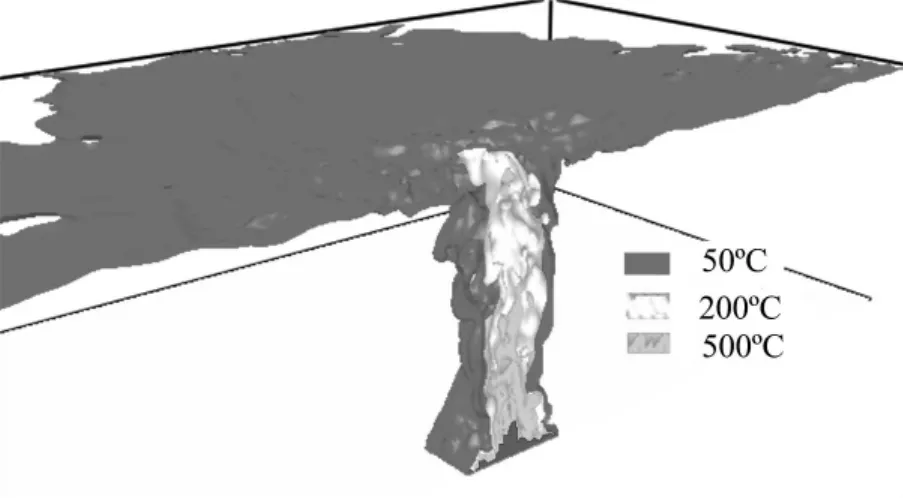
图4 工况一中FDS模拟得到的火场温度分布三维云图Fig.4 3Dcontour view of simulated gas temperature in case one

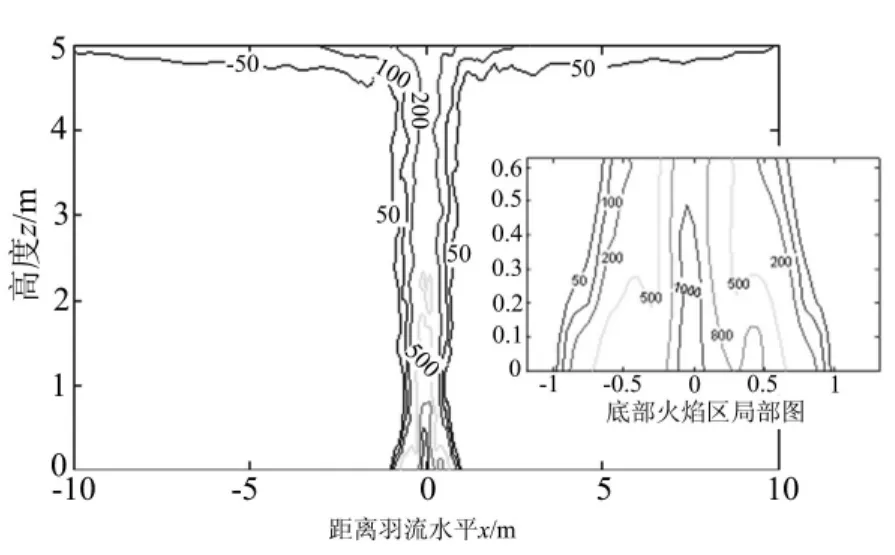
图5 工况一中FDS模拟得到的火源中心面内的温度分布图Fig.5 2Dcontour view of simulated gas temperature at plume center in case one

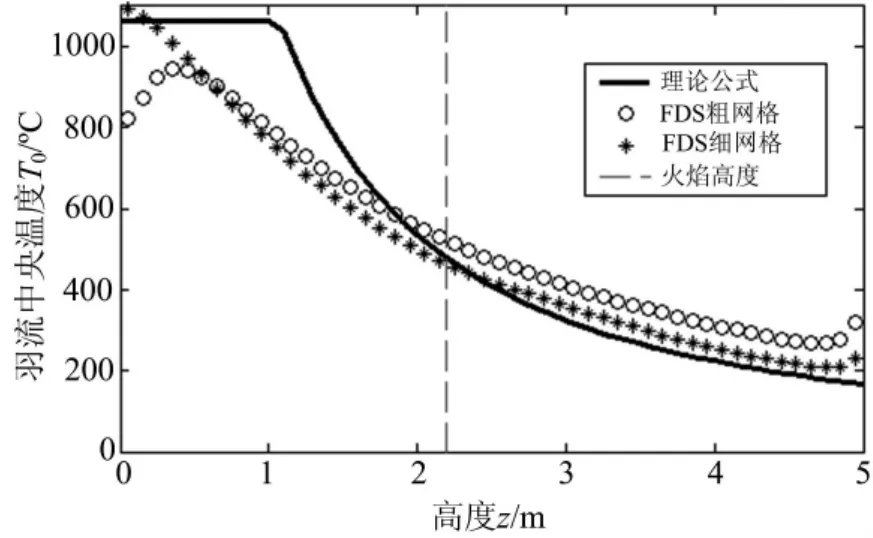
图6 工况一中由公式计算得到的羽流中央温度结果与FDS模拟结果的比较Fig.6 Compare between plume center temperatures predicted by theory and FDS

图6给出了工况一中由公式计算得到的羽流中央温度结果与FDS模拟结果的比较。公式计算中，采用式（11）和式（14）的较小值作为火源中央温度。图中红虚线标明了火焰高度由式（15）计算得到。比较发现，在火焰高度以上，公式与FDS符合很好且公式结果略微偏低；在火焰高度以下，公式与FDS相差较大且公式结果偏高。但在底部火焰区，公式与FDS使用精细网格（R＊＝1／20）得到的火焰温度符合很好，这与之前的研究结果一致［17，22，23］。

图7 工况一中由公式计算得到的顶棚射流最高温度结果与FDS模拟结果的比较Fig.7 Compare between maximum ceiling jet temperatures predicted by theory and FDS

图7给出了工况一中由公式计算得到的顶棚射流最高温度结果与FDS模拟结果的比较。撞击区以外，Alpert给出的公式（图中标记为“Alpert公式”）或式（16）与 FDS 符合很好，Heskestad ＆Hammada给出的公式（图中标记为“Heskestad公式”）或式（17）与FDS符合较差。撞击区域，公式与FDS相差较大，且该区域使用精细网格模拟得到的结果与公式结果更为接近。

考虑计算中使用精细网格得到的结果一般要更为准确，在工况二中将使用单一的精细网格模拟。

图8给出了工况二火灾持续时间内不同高度处由公式计算得到的羽流中央温度结果与FDS模拟结果的比较。2m高度以内，公式与FDS（平均值）符合很好；2m到4m高度内，公式与FDS（平均值）符合较好；4.8m高度或接近吊顶位置处，公式与FDS相差较大。整体而言，公式与FDS符合较好，且公式结果偏低。

图8 工况二火灾持续时间内不同高度处由公式计算得到的羽流中央温度结果与FDS模拟结果的比较Fig.8 Compare between plume center temperatures at different heating time predicted by theory and FDS

图9给出了工况二不同时刻由公式计算得到的顶棚射流最高温度结果与FDS模拟结果的比较。整体而言，“Heskestad公式”或式（17）较“Alpert公式”或式（16）与FDS结果更为接近。对于火灾发展阶段（300s），在撞击区以内，公式与FDS相差较大；撞击区以外，“Heskestad公式”与FDS符合很好；对于稳态燃烧阶段（1500s），“Heskestad公式”与FDS相差较大且偏低，“Alpert公式”在远离撞击区与FDS符合较好，但其他位置与FDS相差很大；对于衰减阶段（3000s），“Heskestad公式”与FDS符合较好且偏低。

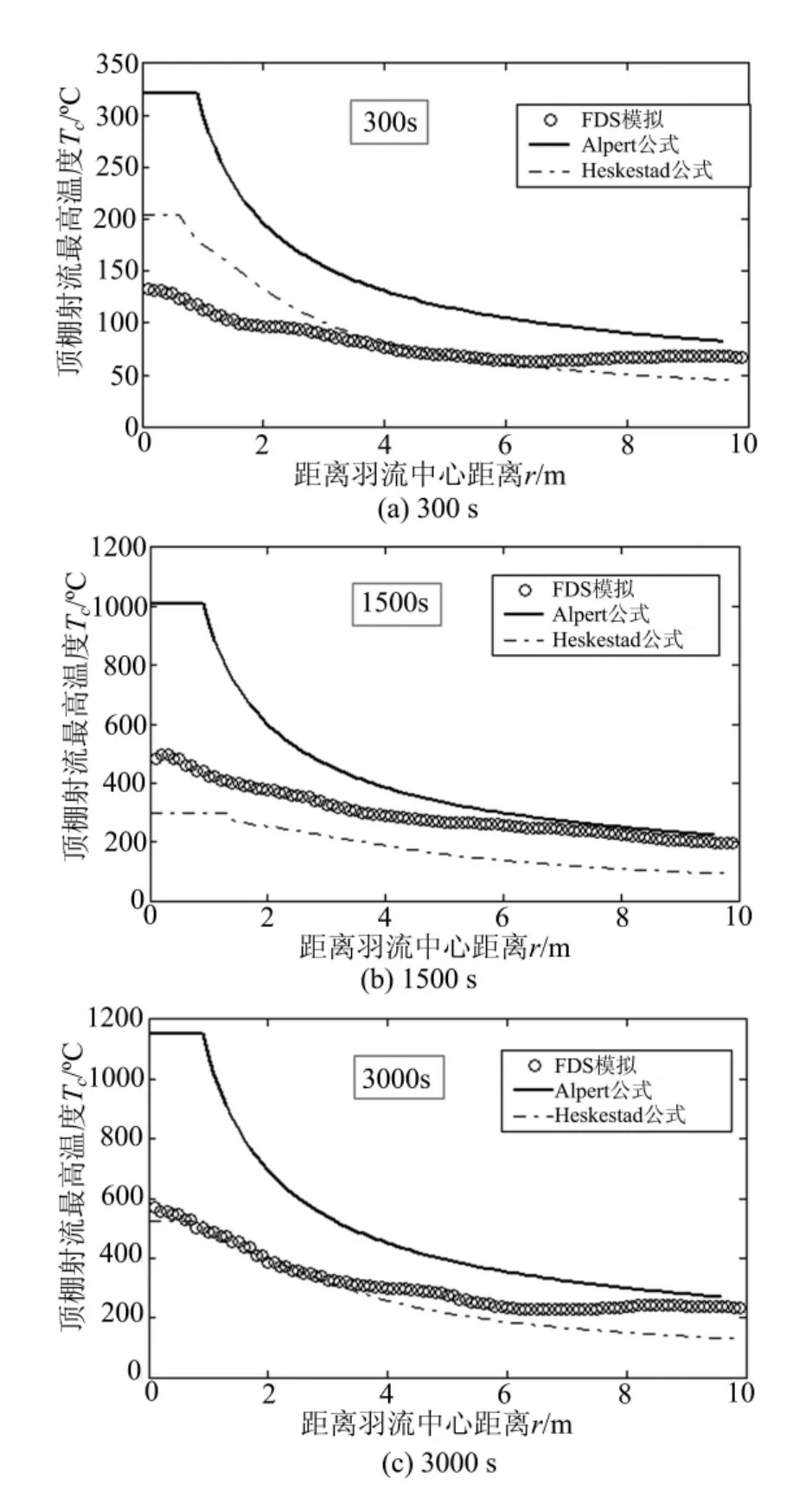
图9 工况二不同时刻由公式计算得到的顶棚射流最高温度结果与FDS模拟结果的比较Fig.9 Compare between maximum ceiling jet temperatures at different heating time predicted by theory and FDS

4.2 讨论

对于所考察的两种工况，公式计算得到的羽流中央温度和顶棚射流最高温度与FDS模拟结果整体符合较好。在火焰区（火焰高度以下），公式结果相对较高，其中部分是式（14）没有考虑多余空气对火焰区温度的降低作用；在烟气区（火焰高度以上），公式结果相对较低。

5 结论与建议

本文介绍了模拟建筑大空间火灾的区域火灾模型并给出了升温计算简单公式。通过与火灾动力学场模拟软件FDS的比较研究得到如下主要结论：

（1）所给出的简单公式是基于火羽流研究相关理论，并引入工程相关常数，公式形式简单，式中参数的物理意义明确，且计算结果与场模拟软件FDS符合很好，推荐用于实际工程计算。

（2）抗火设计中考察最多的中央羽流温度［24］，为便于工程使用，可将推荐的简化公式统一表述如下：

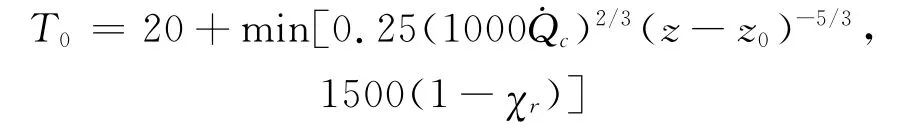
附录：建筑大空间的定义

欧洲规范EC1［25］中并未对建筑大空间进行定义，但在其附录A中，限定了参数火灾模型的适用条件，即楼面面积小于500m2，顶棚无水平开口，且高度不超过4m的房间。因而，可参照欧洲规范认为楼面面积超过500m2，且高度大于4m的空间为大空间。

美国防排烟规范 NFPA92B［26］定义大空间（Large-Volume Space）为：无隔断、高度超过2层楼高、烟气在其中可自由流动的空间。因而，取楼层高度为3.0m，可参照NFPA 92B，认为高度大于6m的空间为大空间。

我国钢结构抗火技术规范CECS200［6］，对高大空间进行了定义，为高度不小于6m，楼面面积不小于500m2的建筑空间。

［1］李引擎.性能化消防设计［M］.北京：中国标准出版社，1999.

［2］李国强，韩林海，楼国彪，蒋首超.钢结构及钢－混凝土组合结构抗火设计［M］.北京：中国建筑工业出版社，2006.

［3］Li GQ，Zhang C.Thermal Response to Fire of Uniformly Insulated Steel Members：Background and verification of the formulation recommended by Chinese code CECS200［J］.International Journal of Advanced Steel Construction，2010，6（2）：788-802.

［4］Zhang C，Li GQ，Wang YC.Sensitivity study on using different formulas for calculating the temperatures of insulated steel members in natural fires［J］.Fire Technology，2012，48（2）：343-366.

［5］EN 1993-1-2.Eurocode 3：Design of steel structures-Part 1-2：General rules -Structural fire design ［S］.British Standard Institution.London，2005.

［6］CECS 200：2006建筑钢结构防火技术规范［S］.

［7］Cadorin JF，Franssen JM.A tool to design steel elements submitted to compartment fires -Ozone V2.Part 1：pre-and post-flashover compartment fire model［J］，Fire Safety Journal，2003，38（5）：395-427.

［8］McGrattan K，McDermott R，Hostikka S，Floyd J.Fire Dynamics Simulator（Version 5）User’s Guide ［R］.NIST Special Publication 1019-5，National Institute of Standards and Technology（NIST），2010.

［9］Quintiere JG.Fundamentals of enclosure fire ‘zone’models［J］.Journal of Fire Protection Engineering，1989，1（3）：99-119.

［10］李国强，杜咏.实用大空间建筑火灾空气升温经验公式［J］.消防科学与技术，2005，24（3）：283-287.

［11］李国强，杜咏.大空间建筑顶部火灾空气升温的参数分析［J］.消防科学与技术，2005，24（1）：19-22.

［12］Chow WK.Assessment of fire hazard in small news agents in transport terminal halls［J］.Journal of Architectural Engineering，2005，11（1）：35-38.

［13］Babrauskas V.Heat Release Rates.SFPE Handbook of Fire Protection Engineering ［S］，Section 3-1，3rded..Society of Fire Protection Engineers，Maryland，USA.

［14］Quintiere JG.Fundamentals of fire phenomena［M］.John Wiley ＆Sons，LTD.2006.

［15］Heskestad G.Fire plumes，flame height，and air entrainment.SFPE Handbook of Fire Protection Engineer-ing［S］，Section 2-1，3rded..Society of Fire Protection Engineers，Maryland，USA.

［16］Quintiere JG，Grove BS.A unifired analysis for fire plumes［A］.27thSymposium （International）on Combustion［C］，The Combustion Institute，1998，27（2）：2757-2766.

［17］Ma TG，Quintiere JG.Numerical simulation of axisymmetric fire plumes：accuracy and limitations ［J］.Fire Safety Journal，2003，38（5）：467-492.

［18］Drysdale D.An introduction to fire dynamics（2ndedition）［M］.John Wiley ＆Sons，1999.

［19］Alpert R.Calculation of response time of ceilingmounted fire detectors［J］.Fire Technology，1972，8（3）：181-195.

［20］Heskestad G，Hamada T.Ceiling jets of strong fire plumes［J］.Fire Safety Journal，1993，21（1）：69-82.

［21］Zhang C，Li GQ.Thermal behavior of a steel beam exposed to a localized fire-Numerical simulation and comparison with experimental results［A］.Proceedings of the Fourth International Conference on Protection of Structures against Hazards［C］，Beijing，China，2009，409-415.

［22］Zhang C，Li GQ.Thermal Response of Steel Columns Exposed to Localized Fires–Numerical Simulation and Comparison with Experimental Results［J］.Journal of Structural Fire Engineering，2011，2（4）：311-317.

［23］Chow WK，Li YZ，Cui E，Huo R.Natural smoke filling in atrium with liquid pool fires up to 1.6MW ［J］.Building and Environment，2001，36（1）：121-127.

［24］Zhang C，Li GQ，Yin YZ，Luo MC.Fire resistance design of large space grid structures by performance-based approach-A case study of the fire resistance design of the roof structure of Kunming International Airport［A］.Proceedings of the Sixth International Conference on Advances in Steel Structures［C］，Hong Kong，2009，776-785.

［25］EN 1991-1-2.Eurocode 1：Actions on structures-Part 1-2：General rules– Actions on structures exposed to fire［S］.British Standard Institution.London，2002.

［26］NFPA 92B.Standard for smoke management systems in malls，atria，and large spaces［S］.National Fire Protection Association，2005.

Simple formulae for calculating the gas temperature in large enclosure fire environment

ZHANG Chao，LI Guo-qiang

（Tongji University，Shanghai 200092，China）

Steel structures are widely used in large enclosure.Limited by its performance and functions，a large enclosure is usually not permitted to be departed by fire walls for preventing horizontal fire spread.Instead，fire loads in the large enclosure are controlled in a special area by using the concept of island，cabin or isolation space in performance-based fire safety design.As a result，the potential fires in the large enclosure are characterized as localized fires.This paper proposes simple formulae for calculating the gas temperature in large enclosure.The formulae are based on the classic plume theory with adopting the commonly used constants in engineering.Case studies for two different fire scenarios are conducted.The calculated results agree well with those by the simulation results using the software of FDS.With a simple form，the proposed formulae are recommended for practical usages.

Large enclosure；Fire；Temperature calculation；Simple formulae；Fire dynamic simulation

TU375.4；X932

A

1004-5309（2012）-0084-08

10.3969／j.issn.1004-5309.2012.02.06

2011-11-30；修改日期：2011-12-29

张 超（1984-），男，湖北潜江人，工学博士，主要从事钢结构抗火。