航空弹药经济批量订货模型研究

朱来辉，曹 炜

（桂林空军学院 广州训练大队，广东 广州 510000）

航空弹药的消耗模式，决定了航空弹药的订货模式，和平时期的订货模型和战时订货模型的结构不同。在平时，由于航空弹药平时消耗的可计划性和可预见性，因此可以考虑采用确定性库存模型，来对航空弹药的订货模式进行研究[1～4]。

1 模型的假设[5～7]

（1）航空弹药有一个预定的存储水平，当存储降至此水平时，可以立即得到补充（即备货时间或拖后时间很短，可以近似地看作零）；不出现缺货，不考虑缺货费用；

（2）对航空弹药的需求是连续的、均匀的，设需求速度为一常数（单位时间的需求量）为常数；

（3）每次订购费不变；

（4）单位存贮费用不变；

（5）在平时训练中，每次使用的都是存储时间最久的弹药，保证存储的都是较新的弹药。

2 模型的建立与求解

建立模型来确定最佳订货间隔和最佳订货批量，目的是在满足军事需求的情况下，使总费用最少。在需求确定的情况下，每次订货数量多，则可减少订货次数，节约订货费；但是，一次订货多，则相应地增加存储费用。因此，综合各种因素确定订货间隔和最佳订货批量，是本模型的关键之所在。

2.1 符号说明

Y表示所有航空弹药仓库总费用；

Yij表示第i个航空弹药仓库第j种弹药在一个周期内的总费用；

Tij表示第i个航空弹药仓库第j种弹药最佳订货间隔；tij表示第i个航空弹药仓库第j种弹药存储时间；Bij为第i个航空弹药仓库第j种弹药在一个订货周期内的平均储量；

Zij表示第i个航空弹药仓库第j种弹药在订货周期内可能的战役需求量与训练需求量之和；

rij表示第i个航空弹药仓库第j种弹药在一个周期内的需求速度，为常数；

Pij表示第i个航空弹药仓库第j种弹药一个周期内最佳订货批量；

cij表示第i个航空弹药仓库第j种弹药订货的单位价格；

lij表示第i个航空弹药仓库第j种弹药每次的订货费用；

qij表示第i个航空弹药仓库第j种弹药的单位存贮费用；

m表示总仓库数；

n表示总弹药种类；

sij表示第i个航空弹药仓库第j种弹药库存水平下限（设定值）。

2.2 模型的建立与求解

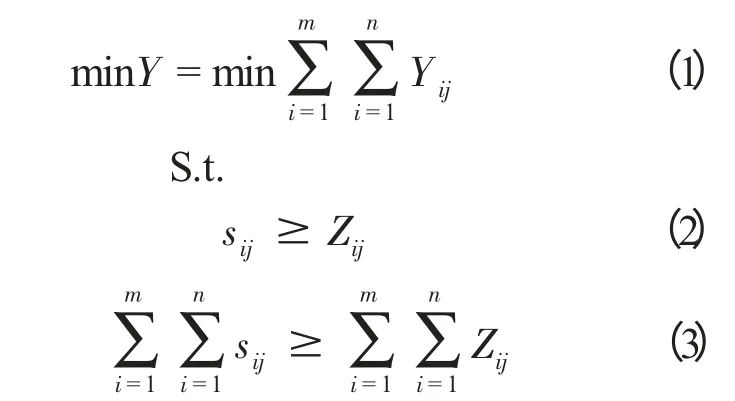
假定每tij时间订货一次，则tij时间的平均储量为

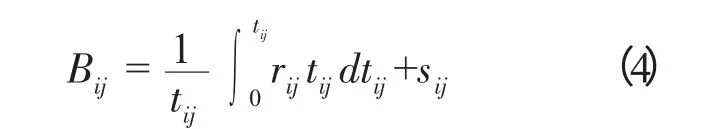
因为rij为常数，化简后得

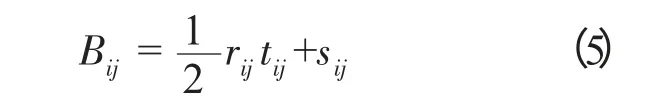
则在tij时间内的总费用为

在tij时间内的平均费用为

要求得平均费用的最小值，只需对上式求导，令其导数为零，得

对式（7）求二阶导数，得

说明此极值是函数的最小值。

因此，最佳订货间隔Tij为

最佳订货批量为

因此，在一个订货周期内最少总费用为

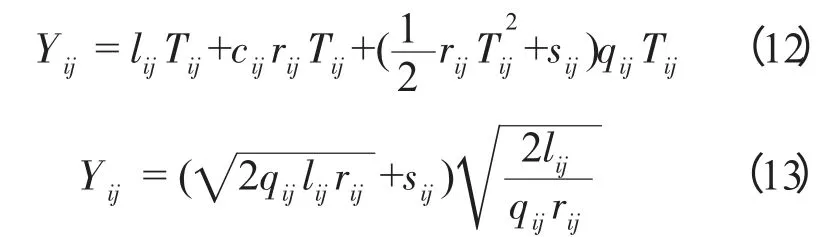
综合式（4）得

由图解法得出和公式推导一致的结果。

图1 确定性存储模型的图解法

3 结束语

该模型的公式结构简单，便于计算。但是本模型做了很多简化，在实际应用中，必须综合考虑多种因素，如各种航空弹药储存寿命、生产周期、生产能力等因素，来确定需要订购的品种和数量。同时也需要考虑订货经费规划和年度经费计划，进行综合平衡，确定一定时间和每年的订货量。由此公式计算出的结果，仅能用于参考。

[1]钱颂迪.运筹学[M].北京：清华大学出版社，2005.

[2]姜启源，谢金星，叶 俊.数学模型（第三版）[M].北京：高等教育出版社，2007.

[3]蒋惠国，程小飞.经济订货（EOQ）数学模型研究[J].武汉理工大学学报，2003，27(4)：527-529.

[4]赵 娜.不确定性条件下供应链优化模型及算法研究[D].大连：大连海事大学，2007.

[5]徐维江，陈学广.弹药保障决策模型的研究[J].军械工程学院学报，2001，13(3)：52-55.

[6]刘金梅，赵国志，韩永要.航空弹药平时消耗量的预测模型[J].弹箭与制导学报，2005，25(3)：212-214.

[7]潘孝先.美国弹药储备的现状与问题[EB/OL].http://www.usa-mil.com，1998.