垂直下降状态下的旋翼三维流场数值模拟
2012-12-19曹义华
曹 栋 曹义华
(北京航空航天大学 航空科学与工程学院,北京100191)
众所周知,直升机流场的数值模拟最困难的问题在于旋翼的流场模拟.之前较流行的旋翼流场计算分析主要专注于悬停和前飞,对下降状态的旋翼流场模拟较少.因为下降的旋翼,当其处于涡环(vertex ring)状态时[1],由于来流速度朝上,远处下游尾迹在旋翼的上方,旋翼诱导速度与相对气流方向相反,两股反向气流相遇形成紊乱的漩涡.同时旋翼的桨尖涡不能被吹离旋翼而聚集在一起,旋翼排出的部分气流又被吸入,绕旋翼外缘打转,流态复杂且很不稳定.1982—2003年,3/4的直升机事故与进入涡环状态有关[2].
对直升机旋翼流场的数值模拟,通常采用两种方法.一种是致力于模拟旋转桨叶附近的细致流动,包括捕捉桨叶附近的激波,分析桨尖涡的形成过程等.一般需要在每片桨叶周围生成贴体网格,将大部分网格点集中于桨叶附近,尤其是桨叶的边界层内,这种方法可以准确得到桨叶附近的流动特性.不过为了提高远场尾迹的计算精度也必须保证远场的网格密度,这将导致网格数目过大,计算代价很高.而采用一些尾迹模型来求解也会存在一些问题,因为尾迹结构会随着飞行条件和桨叶结构的改变而变化.对于垂直下降飞行,特别是涡环,湍流状态时由于气流对冲,很难有合适的尾迹模型能很好地描述.
本文采用另一种方法,将旋翼简化为一无限薄激励盘,忽略旋翼桨叶附近的细致流动特征,采用动量叶素理论结合下降状态时的诱导速度经验公式来计算桨叶的载荷分布,通过在N-S(Navier-Stokes)方程中加入此分布的载荷(桨盘压力差)来代替旋翼对空气的作用.由于用围绕整个桨盘的网格取代围绕桨叶的贴体网格,减小了网格生成的难度和网格数目,从而有效地节省了计算时间并能保证一定的计算精度.国外,文献[3]等采用这种方法对旋翼的流场进行了分析,而国内文献[4]等也使用这种思想进行了旋翼三维流场的研究,但他们都仅限于悬停和前飞,本文通过对旋翼垂直下降进行数值模拟,对旋翼下降时的流场和性能预测有一定的参考价值.
1 控制方程和湍流模型
由于垂直飞行时具有轴对称特性,理论上不同方位角的流动特性相似,且本文采用的模型旋翼的桨尖速度较小且整个旋翼的流场速度也不大,因而将整个流场看作不可压有粘流动,所以采用非定常、不可压、湍流的N-S方程为控制方程.并结合使用S-A(Spalart-Allmaras)一方程的湍流模型,此湍流模型可以很好地适用于翼型、壁面边界层等流动.控制方程的通用形式如下:

式中,Φ为广义变量;ρ为空气密度;V为速度矢量;Γ为广义扩散系数;SΦ为广义源项.对于特定意义的Φ,具有特定的Γ和SΦ.式(1)中的4项分别是非定常项、对流项、扩散项和源项.由于不考虑热传导,SΦ仅存在动量方程中,表示单位体积内旋翼赋予流场的气动力,对于本文采用的无限薄作用盘而言,仅表示了单位面积的旋翼赋予流场的拉力(压力)差.
2 计算方法
本文计算时利用商用软件直接求解三维粘性不可压N-S方程,微分方程的离散使用有限体积法,压力速度耦合迭代选用著名SIMPLER(Semi-Implicit Method for Pressure-Linked Equations Revised)算法,对流项使用二阶迎风差分格式离散,离散得到的代数方程组用Gauss-Seidel迭代法求解.而旋翼桨盘的压力分布则由FORTRAN编程得出,再通过多项式拟合成自定义函数(UDF)加载到商用软件中.
2.1 压差分布计算
从图1中可以看出,为了求得桨叶翼型剖面上的升力和阻力,需要用到叶素相对速度U,可表示为
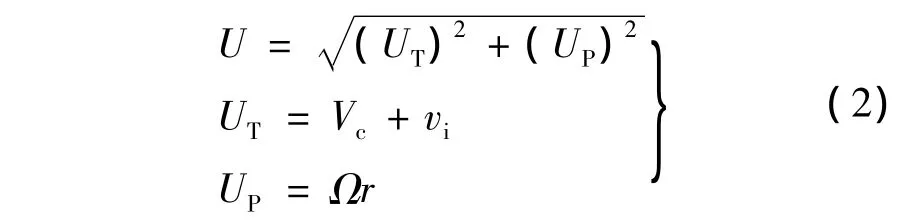
式中,UP,UT分别为桨叶剖面的切向速度和轴向速度;Ω,r分别为桨叶旋转角速度和桨叶剖面径向位置;Vc,vi分别为旋翼桨盘下降速度和与之对应的诱导速度,考虑到在一定的下降速度下,经典的动量理论不再成立,文献[5]给出了一种近似的诱导速度分布,vi可表示为

而悬停诱导速度vh可表示为
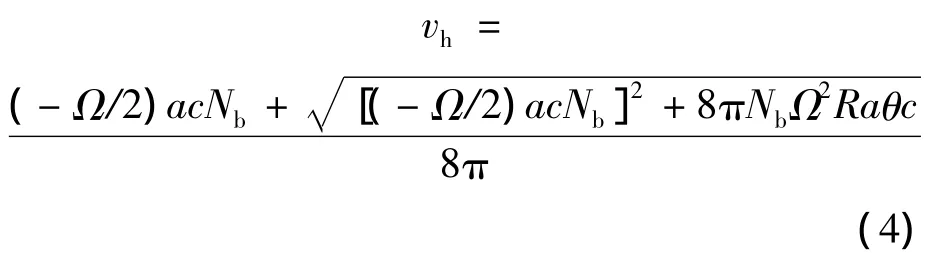
式中,a,c,Nb,R 分别为升力线斜率、桨叶宽度、桨叶片数和旋翼半径;θ为桨距角.

图1 桨叶翼型剖面上的气动力
根据迎角、当地雷诺数和马赫数,以及剖面的翼型型号,可以得到翼型的升力系数Cl和阻力系数Cd.本文通过FORTRAN程序计算了不同剖面迎角和下降速度下的升力系数和阻力系数,从而,桨叶剖面上的升力和阻力分别为

同时,来流角β和攻角α可分别表示为
则微段拉力dT和微段扭矩dQ可简单地表示为
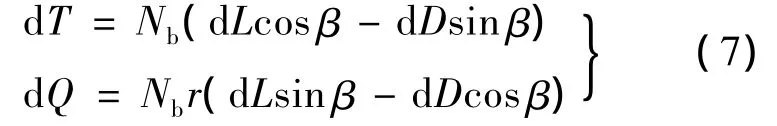
然后通过积分求解,可得到整个桨盘的拉力和扭矩,而桨盘上的压强分布则可表达为
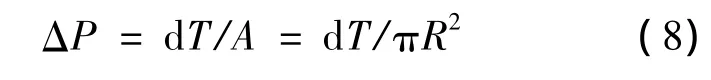
通过不同的桨盘径向位置,可以得到不同的ΔP,本文是将桨盘沿径向分为40个微段,这样可使后面的曲线拟合获得足够精确的结果,图2给出了压差源项的计算流程.对于悬停状态下的模型旋翼(桨盘半径为0.914 m),拟合后的公式为
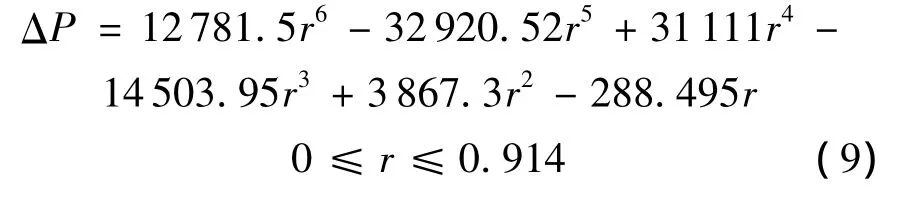
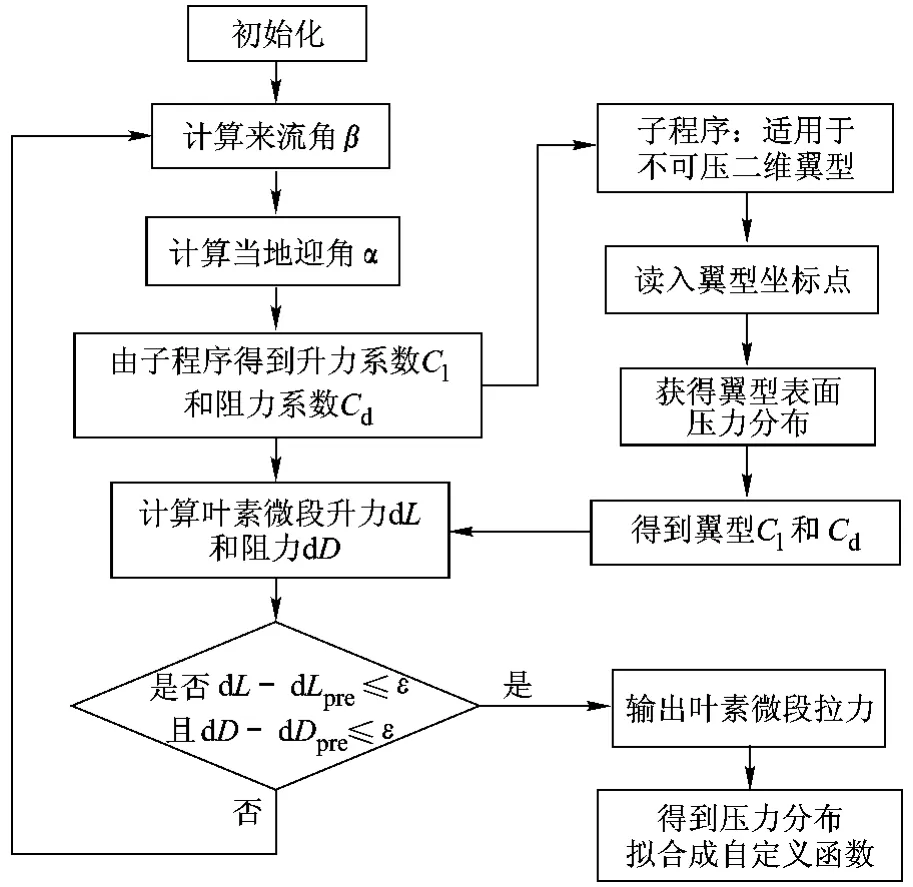
图2 动量源项桨盘压力差的计算流程图
2.2 网格生成与边界条件
为了兼顾计算精度与速度,本文利用GAMBIT前处理软件生成了六面体结构化网格,计算域为包含旋翼的圆柱体,网格在旋翼附近分布较密,离开旋翼逐渐变稀.垂直飞行时,选取半径为10R、高为30R的计算域,为了满足垂直下降的流场分析,桨盘上部的网格计算域高度为下部的两倍,网格数共有1 098 540个,见图3.为了符合模型旋翼附近的不可压流场状况,将整个计算域外表面定义为速度进口边界,桨盘定义为风扇边界,其上将加载由前面计算得到的压力分布源项,而桨毂则设定为壁面边界条件.

图3 计算域网格划分
2.3 悬停算例验证
为了能与现有的实验结果对照,本文采用了S-A湍流模型计算了模型旋翼桨盘下方0.104R,0.215R,0.660R 及0.993R 位置处的动压分布,旋翼参数见文献[6].图 4、图 5给出了 0.104R,0.660R处的计算结果与实验结果[6]对比.从图中可以看出,采用本文方法得到的悬停旋翼的下洗流场动压分布与实验值的变化情况基本吻合,为后文的垂直下降算例计算奠定了基础.
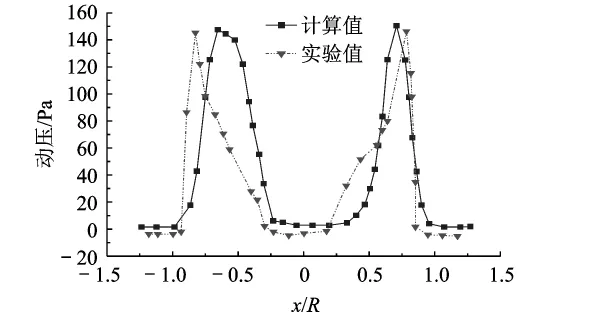
图4 桨盘下方0.104R处的动压分布
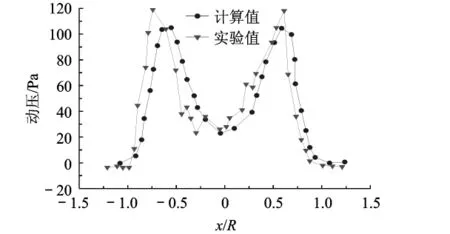
图5 桨盘下方0.660R处的动压分布
3 算例计算与分析
采用上文中提到的方法,本文模拟不同下降率的旋翼流场,从小下降率1 m/s到高下降率的19 m/s,并绘出了不同下降率下的流场流线特征(见图6),流场速度分布和旋翼性能预测图(包括拉力和攻角变化),并分析了产生变化的原因.

图6 不同下降率下的旋翼流场流线图
3.1 小速度下降情况
对应于图6中Vc=1 m/s和3 m/s的情况,可以看出由于下降率较小,向上的气流很难抵消旋翼自身下洗气流的影响,直到桨盘下方较远处下洗速度有所减弱后,两股相对气流对冲才卷起较大的涡,但由于其距桨盘较远,对旋翼的性能影响不是太大.图7a给出了Vc=1 m/s时计算域中截面(y=0)处的速度矢量图,明显可以看出旋翼的下洗速度仍占主导地位,仅在离桨盘周边很远处才有向上的速度分布.而图7b则捕捉到了小速率下降时旋翼上方的速度鞍点(速度为0的点,位于正中央),证明了旋翼在小速率下降的情况下旋翼上方由于流场不连续所导致的非定常特征.
图8给出了悬停以及Vc=1 m/s和3 m/s时,桨盘下方0.660R处的垂向速度Vz分布,其中悬停时,桨盘中心区域(r/R≤0.3)的诱导速度为正(定义相对气流方向向上为正),即形成了一个较大的上洗区域,而随着下降率的增加,此上洗区域消失.直到旋翼进入涡环状态,见图9,又出现了部分上洗的情况.
3.2 涡环及湍流状态
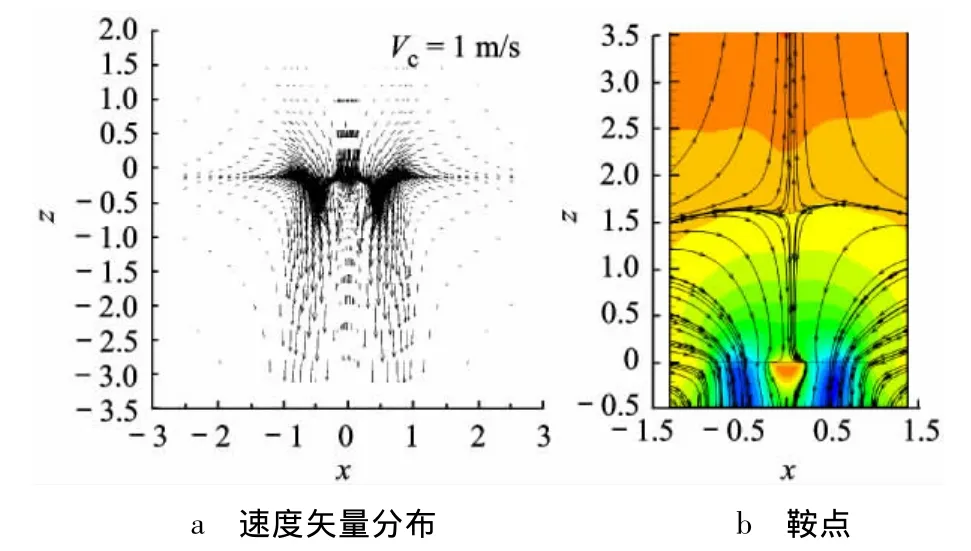
图7 小下降率情况下的中截面(y=0)处的特征分布
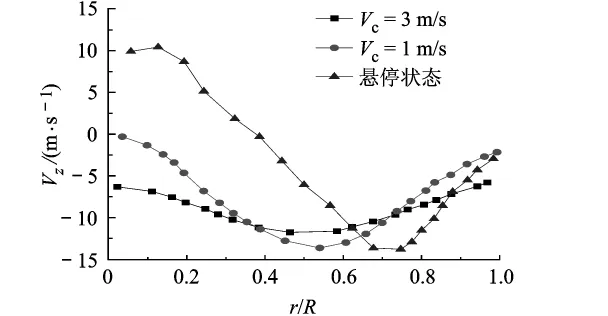
图8 小速度下降时桨盘下方0.660R处的Vz分布
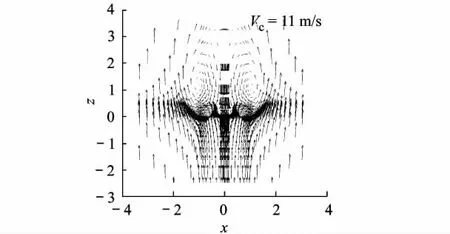
图9 湍流状态下的中截面处的速度矢量分布
一般认为当Vc=0.7vh时,旋翼进入涡环状态,本模型旋翼计算得到的vh≈7 m/s,所以可以认为图6中的Vc=5 m/s已进入涡环,由于下降率的增加,向上的自由流使桨尖涡螺旋线堆积在桨盘的下方,桨尖涡开始呈辐射状从旋翼桨盘向外发展,形成了靠近桨盘的环状情形.当下降率继续增加,对应于图6中Vc=7 m/s以及9 m/s的情况,桨尖涡环有所缩小并逐步靠近桨盘,形成了成熟的涡环状态.由于旋翼不断旋转,涡环强度不断积累,甚至出现了左右不对称的情况,所以整个流场的非定常特性十分明显.
当Vc=11 m/s时,形成的涡环上移至桨盘上方,旋翼进入湍流状态,在这种状态下,气流仍然会有高水平的扰动,但是,因为桨盘处的速度向上,所以穿过旋翼的环流少了很多.旋翼承受着由湍流造成的某些颠簸,但没有涡环状态时明显,图10中的垂向速度分布也证明了这点.图9、图11分别给出了Vc=11 m/s和9 m/s时计算域中截面(y=0)处的速度矢量图,明显可以看出旋翼向上的自由流速度已占主导地位.而图11中的典型涡环状态的速度矢量分布与文献[7]采用PIV实验得到的结果有明显的相似(图12),对比图9、图11,前者的自由流强度更加明显,且形成的速度湍流已移至桨盘上方.
图10 给出了 Vc=5,7,9,11m/s时,桨盘下方0.660R处Vz沿桨叶径向位置的分布,相比于小速度下降状态,在涡环形成阶段,z轴方向速度变化并不明显,其绝对峰值并未因下降率的增加有所减少甚至有所增加,从-12.5 m/s变为-15 m/s(定义相对气流方向向上为正,则下洗气流方向为负),非定常的气流特征开始呈显;当进入完全发展的涡环状态,对应于Vc=9 m/s时,增加的下降率对Vz的影响趋于明显,同时在此截面处沿桨叶径向,速度方向发生改变,与悬停情况类似,在内侧速度为正,气流方向向上,外侧速度为负,气流方向向下.但上洗的范围有所扩大(r/R≤0.55),相反地,气流方向导致空气动力特性十分复杂,这也与其所对应的速度矢量图相符合,靠近内侧速度矢量向上,靠外侧速度矢量向下.而当旋翼处于湍流状态时(Vc=11 m/s),Vz沿桨叶径向变化趋于0且均为正,即在此处位置,向上的自由流已完全抵消了旋翼的下洗作用.而湍流状态的速度矢量图显示,形成的环状气流已经发展到旋翼上方,桨盘下方的的流场较为稳定.
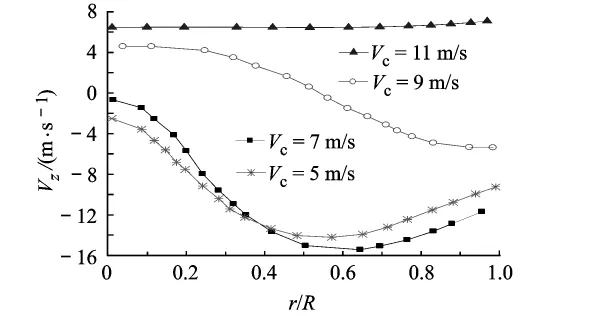
图10 涡环及湍流时桨盘下方0.660R处的Vz分布
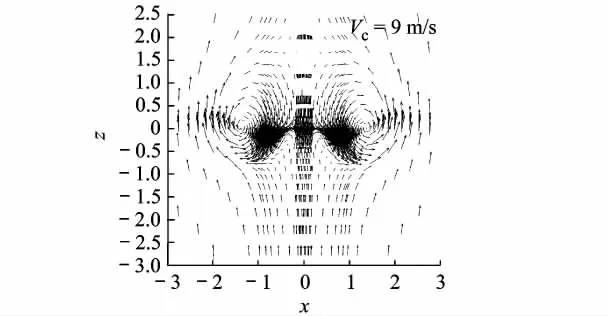
图11 典型涡环状态下的中截面(y=0)处的速度矢量分布
3.3 风车状态
稳定的风车状态(一般Vc≥|1.8vh|)对应于
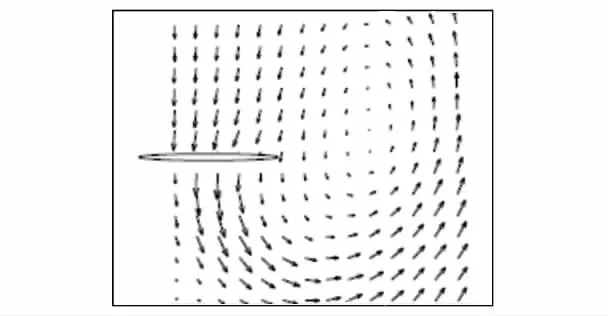
图12 文献[7]利用PIV实验得到的典型涡环状态下单侧桨叶的速度矢量分布
图6中的Vc=15 m/s,此时气流从桨盘下方向上穿过桨盘平面,流场又趋于稳定,图13给出了Vc=15 m/s时计算域中截面(y=0)处的速度矢量图,由于自由来流速度较大,完全抵消了旋翼的下洗流速度,流场中相对气流方向都已完全向上.而图14则给出了Vc=13,15,17m/s时,桨盘下方0.660R处Vz沿桨叶径向位置的分布,与涡环和紊流状态相比,速度值皆为正(即速度方向向上),且沿桨叶径向分布区域平缓,流场变得稳定起来.

图13 风车状态下中截面处的速度矢量分布

图14 风车状态时桨盘下方0.660R处的Vz分布
3.4 垂直下降性能预测
前面对流场的分析更主要是为了得到旋翼在下降情况下的性能特征,旋翼性能与流场诱导速度相互关系如图15所示,可以看到两者相互影响,存在一定的耦合.
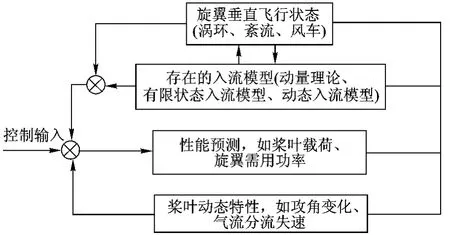
图15 旋翼载荷与诱导速度及垂直下降飞行的关系
本文采用两种方法给出了下降飞行时固定桨距情况下的平均拉力,见图16,可以看到两种方法都在完全的涡环状态(或湍流状态初始)时出现最大的拉力损失,即 -1.6≤Vc/vh≤ -1.3,恰巧的是,本文计算和实验[8-9]都显示,在这个范围里平均诱导速度也达到峰值,见图17.因此不难理解入流的增加正是导致拉力损失的关键,这与文献[10]的解释类似.至于在 Vc≥15 m/s后,两种方法的计算结果偏差明显,可能的原因是在编制程序中并没有涉及桨叶失速[11]的情况,因为按照文献[5]中的初始诱导速度分布特性,在高下降率的情况下,桨叶剖面攻角早已超过了NACA0012翼型的失速攻角,如图18所示,所以得到的结果偏大.
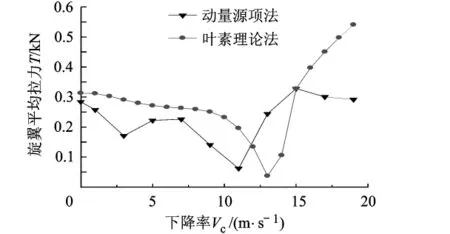
图16 不同下降率下的桨盘平均拉力
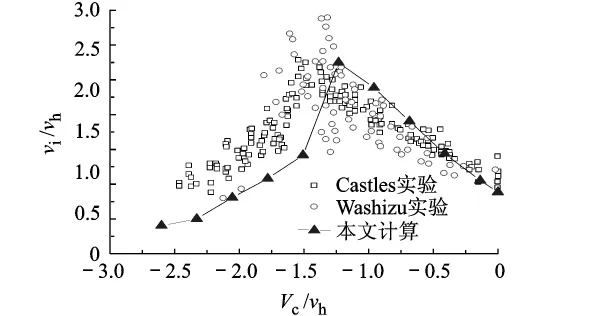
图17 模型旋翼垂直下降状态的诱导速度分布
在得到桨盘平均拉力和诱导速度之后可以很容易计算出模型旋翼的功率,见图19,与文献[8]吻合较好.其中Ph为悬停时的功率值,可以看到虽然在涡环状态的情况下,拉力有较大的损失,但由于诱导速度的增加,得到的需用功率值仍要大于悬停的需用功率,而在风车状态的情况下,特别是 -1.8≤Vc/vh≤ -1.6的范围里,旋翼功率甚至小于悬停时的需用功率,旋翼向周围的空气吸收能量.

图18 不同下降率下桨叶攻角的径向分布
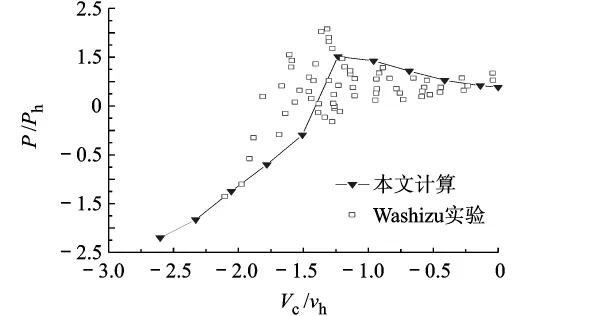
图19 模型旋翼垂直下降状态的需用功率分布
4 结论
本文通过引入压力源项求解非定常、不可压、湍流的N-S方程,来模拟直升机旋翼的垂直下降飞行情况.这种CFD(Computational Fluid Dynamics)分析方法,只需要知道旋翼桨叶的几何特征和气动特性参数,通过FORTRAN程序将得到的压力分布以UDF的形式代入软件耦合求解就能得到旋翼的全部三维流动信息,比如,不同下降率情况下旋翼附近的流态特征和某一截面的速度分布.同时计算得到了不同下降率下旋翼诱导速度分布以及拉力和功率分布,计算结果与文献吻合较好,并验证了在涡环状态下,旋翼拉力损失主要是由增加的诱导速度造成的.
此外,本研究还具有一定的实际意义:比如更改网格后可分析不同的旋翼参数(桨叶负扭度、桨叶半径等)对下降飞行时旋翼性能的影响,包括对涡环发生边界的准确预测,这对新型旋翼设计以及如何避免进入涡环状态有一定的参考价值.目前正在进行一些后续的工作,如采用准确桨叶建模结合滑移网格取代激励盘模型,可控的桨距变化取代固定桨距,以及机身对旋翼性能的影响等.
References)
[1]普劳蒂.直升机性能及稳定性和操纵性[M].高正,译.北京:航空工业出版社,1990:77-79 Prouty R W.Helicopter performance,stability and control[M].Translated by Gao Zheng.Beijing:Aeronautical Industry Press,1990:77-79(in Chinese)
[2]Varnes D J.Development of a helicopter vortex ring statewarning system through a moving map display computer[D].Monterey,California:Department of Aeronautics and Astronautics,Naval Postgraduate School,1999
[3]Chaffin M S,Berry J D.Helicopter fuselage aerodynamics under a rotor by Navier-Stokes simulation[J].Journal of the American Helicopter Society,1997,47(3):235 -243
[4]于子文,曹义华.前飞旋翼三维湍流场的数值模拟[J].北京航空航天大学学报,2006,32(7):751-754 Yu Ziwen,Cao Yihua.Three dimensional turbulence numerical simulation of rotor in forward flight[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(7):751 - 754(in Chinese)
[5]Leishman J G.Principle of helicopter aerodynamics[M].Cambridge:Cambridge University Press,2006:81 -91
[6]McKee J W,Naeseth R L.Experimental investigation of the drag of flat plates and cylinders in the slipstream of a hovering rotor[R].NACA TN 4239,1958
[7]Green R B,Gillies E A,Brown R E.The flow field around a rotor in axial descent[J].Journal of Fluid Mechanics,2005(354):237-261
[8]Washizu K,Azuma A,Koo J,et al.Experiments on a model helicopter rotor operating in the vortex ring state[J].Journal of Aircraft,1966,3(3):225 - 230
[9]Castles W,Jr,Gray R B.Empirical relation between induced velocity,thrust,and rate of descent of a helicopter rotor as determined by wind-tunnel tests on four model rotors[R].NASA TN 2474,1951
[10]Azuma A,Obata A.Induced flow variation of the helicopter rotor operating in the vortex ring state[J].Journal of Aircraft,1968,5(4):381-386
[11]苏媛,曹栋,曹义华.计及大迎角失速的直升机旋翼的气动力模拟[J].北京航空航天大学学报,2010,36(2):168-171 Su Yuan,Cao Dong,Cao Yihua.Simulation of helicopter rotor aerodynamic force in conditions of high angle of attack and dynamic stall[J].Journal of Beijing University of Aeronautics and Astronautics,2010,36(2):168 -171(in Chinese)
