基于数据挖掘技术的软件缺陷检测方法研究

华中科技大学计算机科学与技术学院 雷 珂 何 威

1.引言

随着软件应用规模的日益扩大和软件应用环境的日益复杂，因为软件质量导致的事故给人们造成的损失越来越多，后果也越来越严重，比如IBM360操作系统的失败、阿丽亚娜号航天火箭的爆炸[1]等。为保证软件的质量，必须检测软件缺陷并对其加以控制。

检测软件缺陷，通常指检查代码缺陷，其方法有很多种，包括人工审查、动态测试和静态分析。程序语义分析方法是静态分析常用的一种分析技术。它通过分析程序的控制流和数据流以及函数调用关系等计算程序的多种语义表示，如调用图和依赖图，来辅助软件审查。这种方法最大的优点就是不必执行目标程序，就可以通过扫描并分析程序的源代码并查找代码中的特定模式（可以理解为编程规则）集合，较早地发现程序代码中的缺陷。

最新的静态分析工具将数据挖掘技术（通常是频繁子图挖掘算法）与程序分析相结合。为了构造一个针对某一种类型的软件缺陷的高效的静态分析工具，必须使用适当的频繁子图挖掘算法。而该类静态分析工具的效率、性能的关键也就是频繁子图挖掘算法。

FFSM[5]算法是基于模式增长方法的。它与目前主流的频繁子图挖掘算法AcGM[2]、FSG[3]和gSpan[4]等方法相比，时间复杂度最优、挖掘效率最高。它使用CAM来唯一标识图，使用FFSM-Join和FFSMExtension来扩展频繁子图，并通过相应的剪枝策略来获得候选子图。在计算支持度时，只对embedding list进行扫描，提高了计算的速度和效率。但是FFSM算法存在一定的局限性，有如下五个主要问题：

不能处理多重图（即两个节点之间可能存在一条以上的边）；

只能处理无向图；

FFSM-Extension需要对边和节点进行枚举，效率低；

无法输出有向频繁子图。

FFSM挖掘得到的频繁子图无法准确地表征规则，无法应用到软件缺陷检测中，实用性差。

针对上述提出的经典频繁子图挖掘算法存在的问题，本文在经典的算法FFSM的基础上，提出了一种新的频繁子图挖掘算法HFFSM（High-performance Fast Frequent Subgraph Mining）。本文的主要工作概述如下：

提出一种将有向标记图等价转换为无向标记图的方法，即该方法可以在有向图转换为无向图之后保留原图边的方向性。而且该方法简单、通用、可移植。

基于经典频繁子图挖掘算法FFSM，提出一个能处理有向多重图并得到有向频繁子图的，比FFSM效率更优的频繁子图挖掘算法HFFSM。

2.FFSM算法介绍

FFSM算法使用邻接矩阵表示图，按照从上到下，从左到右的顺序扫描邻接矩阵的下三角，包括对角线，将得到的串表达式称为图的代码，将最大的代码称为图的规范表示，并把相应的邻接矩阵称为图的CAM（Canonical Adjacency Matrix）。

FFSM算法的基本思想如下：

(1)FFSM算法利用CAM来唯一标识图。

(2)简化输入数据库中的图为无向简单图并利用CAM的性质来解决子图同构问题。

(3)FFSM算法利用FFSM-Join和FFSMExtension操作来生成候选子图。FFSMJoin根据k-频繁子图所属类型的不同，采用不同的方式进行合并，生成k+1-频繁子图。FFSM-Extension每次在频繁子图上添加一条边和新的节点来获得新的频繁子图。

图1 FFSM算法的核心思想

图2 添加虚拟节点处理多重图

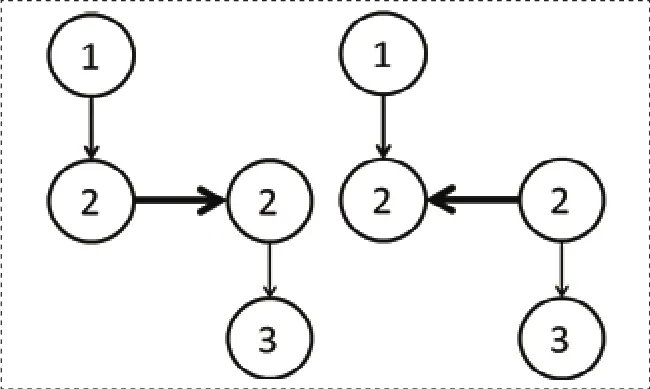
图3 边方向性处理方案无法处理的例子

(4)剪枝：去除既非次优CAM也非频繁的子图。

图4 FFSM-Extension伪代码：

图5 FFSM-Extension伪代码

输入图集中，与k-频繁子图具有子图同构关系的所有图，称为Embedding list。k+1-频繁子图的支持度可以通过扫描Embedding list获得，提高了支持度的计算速度如图1所示。

3.HFFSM算法

针对第一部分提到的FFSM的种种缺陷，本文针对第一部分中提出的HFFSM频繁子图挖掘算法的缺点，对原FFSM算法做出以下几点改进：

(1)问题一解决方案：多重图等价转换为简单图

HFFSM算法无法处理多重图，但是两个顶点之间可能同时存在数据依赖和控制依赖或控制依赖边和共享数据依赖边，所以必须将多重图转换为简单图。

杨炯等人[6]提出虚拟节点的概念，对多边情况进行处理，转化为单边。他们为了处理一对节点间的多条边，使用一条长度为2通过一个新的虚拟节点连接到原终点的路径来代替每一条多出来的边。

如图2所示，当节点1和节点2之间存在多条边时，每一条多出来的边通过添加一个虚拟节点将其转换为长度为2的路径。

(2)问题二和问题四解决方案：有向图等价转换为无向图

由于HFFSM算法只能处理无向图，而静态分析得到的PDG图却是有向标识图，所以必须将其转换为无向标识图。

有一个可选方案是，直接忽略边的方向性，这也是很多其他算法包括FFSM采取的处理方式。从2.2节对PDG的介绍可以看出，从节点a到b的数据或控制依赖与从节点b到a的数据或控制依赖在语义上是不等价的。直接忽略边的方向性必然导致得到图无法准确反映程序内部元素之间的语义关系，挖掘得到的规则也极有可能是虚假规则。

本文提出一个新方案来解决该问题。首先给出一个定义，以便于对边的方向进行处理。

定义1：大边和小边

给定边e＜a, b＞，la和lb分别是顶点a和b的标签。如果la＞lb，则边e为大边；否则，边e为小边。

新方案包含如下三条规则：

大边的标签用大写字母表示，小边的标签用小写字母表示；

忽略共享数据依赖边的方向，标签统一用小写字母表示；

添加虚拟节点之后边的方向由原来边的方向确定。

按照上述三条规则对原图进行处理，就可以通过标签的大小写区分从节点a到b和从节点b到a的边，同时大写意味着边的方向是通过标签大的节点指向小的节点，小写意味着边的方向是通过标签小的节点指向大的节点。

但是该方法存在一个缺陷——当边两个顶点的标签相等时，使用该方法无法保证得到的无向图与有向图在语义上等价。如图3所示，用上述方法处理完之后，左图和右图等价，但是它们在语义上并非等价。

但是，两个顶点之间的边是属于数据依赖或控制依赖或共享数据依赖，同一类型的语句(顶点)间不会存在边(即使存在，在规则中这样的边是没有意义的，可以忽略)，所以不用考虑边的两个顶点的标签相等的情况，这就意味着，在本文的问题范围内上述缺陷是不需要考虑的。

总之，通过上述三条规则，可以在本文的问题范围内(在挖掘编程规则时)将有向PDG图等价转换为无向标记图。

因为该方法在将有向图转换为无向图时保留了图中边的方向性，所以解决了问题二。通过边的标签的大小写可以判断边的方向，即大写意味着边的方向是通过标签大的节点指向小的节点，小写意味着边的方向是通过标签小的节点指向大的节点。因此可以将挖掘得到的无向频繁子图还原为有向频繁子图，解决了问题四。另外，本方案是针对于标记图，所以可以很方便的移植到同类算法中去，如gSpan。

(3)问题三解决方案：FFSM-Extension的改进

FFSM-Extension操作是向CAM添加一条从一个新节点到CAM最后行表示的节点的边。其有两个限定条件：

CAM必须是outer矩阵(矩阵最后一行除对角线元素之外有且仅有一个非0元素)。

添加的边必须是CAM最后一行表示的节点到一个未在CAM中的节点的边。

FFSM-Extension伪代码，如图4所示。

一个图是频繁的，那么图中的每个节点和边必然也是频繁的。根据这个性质，利用前面提到的频繁单节点矩阵集和频繁边集可以对FFSM-Extension进行优化。

从频繁单节点集中去除已经在M中的节点，然后遍历频繁单节点集。对于其中的每一个节点，检测其和M的最后一行表示的节点间是否存在边，若存在其且未包含在M中而包含在频繁边集中，则添入该节点和边生成新的矩阵。利用该方法可以避免产生一些非频繁的矩阵。要检验每个矩阵是否为次优CAM、是否频繁，这些都会带来资源的消耗，所以尽量减少非频繁矩阵的产生可以带来效率的提高。FFSMExtension伪代码，如图5所示。

4.实验

4.1 实验环境

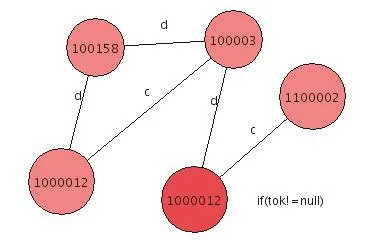
图6 频度为5时FFSM输出的一个频繁子图

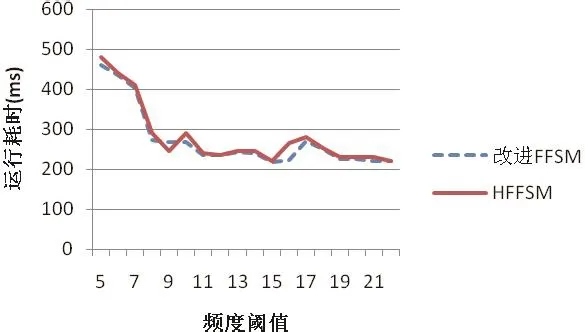
图8 HFFSM VS FFSM在不同频度阈值下运行耗时

HFFSM算法采用Java技术实现。

实验运行的硬件环境：

CPU是Intel(R)Core(TM)2 Duo CPU T6400(2.00GHz)，

一级缓存128KB，二级缓存2MB，

RAM是DDR2 800MHz 2.00GB。

实验运行的软件环境：

操作系统是Windows 7旗舰版32位，

编译软件是Eclipse SDK v3.7.1和jdk1.7.0、jre7。

4.2 实验内容

本部分主要比较HFFSM算法和改进过FFSM-Extension后的FFSM算法的性能。

①输出结果分析比较

图6是频度阈值为5时，FFSM算法输出的一个频繁子图，图7是其文本输出。

与HFFSM输出的结果不同，因为FFSM算法只能处理和输出无向图，从图3和图4很难判断其对应的源程序代码，以及其代表的规则的含义，也就是说，FFSM挖掘得到的结果无法表征编程规则，在实际应用中基本无法使用。

而HFFSM算法输出的是有向图，通过边的方面可以知道程序的执行规则，从而可以还原图为超图中的源代码，便于理解规则的含义。

综上所述，FFSM算法只能输出无向频繁子图，HFFSM算法可以输出有向频繁子图。FFSM算法无法准确表征编程规则，HFFSM算法不仅可以准确表征编程规则，还可以将规则还原为相应的源代码，比FFSM算法具有更高的实用性。

②不同频度阈值下的运行耗时

图8是HFFSM和FFSM在不同频度阈值下运行耗时的图。

图7 图6的文本输出

由图8可知，HFFSM和改进FFSM-Extension后的FFSM在运行时间，即算法运行的时间效率上基本没有差别，所以本文对FFSM的改进并未造成算法效率的降低。

由于对于FFSM的改进是将新的操作插入到原算法的实现中，例如对方向性的改进就是在解析输入PDG图文件时判断大小边对标签进行处理。所以，保证了改进算法时效率基本等效。

5.总结

采用静态分析技术可以较早地发现程序代码中的缺陷，以便于得到高质量的软件。但是，没有一种软件缺陷检测技术能够检测所有的软件缺陷，静态分析技术只能查找某些特定模式或规则。为了处理有向多重图、得到有向频繁子图并提高算法效率和实用性，尤其是减少算法应用时的虚假警报，本文在经典的算法FFSM的基础上，提出了一种新的频繁子图挖掘算法HFFSM。通过实验表明，本文算法比FFSM在时间效率上略有提高，但是避免了输出的一些错误的频繁子图，提高了算法的准确率。同时，算法输出的频繁子图是有向图，能够更加精确地表征规则，提高了算法的实用性。由于频繁子图挖掘算法和图结构都很复杂，处理时难度较大，本文算法仍有许多不足亟待解决。

[1]郑人杰.软件用户盼望获得精品[J].测控技术,2000,19(2):1-5.

[2]A.Inokuchi,T.Washin,K.Nishimura,H.Motoda.A Fast Algorithm for Mining Frequent Connected Subgraphs.Research Report RT-0448,IBM Tokyo Research Lab,2002.

[3]M.Kuramoehi,G.Karypis.Frequent Subgraph Discovery.Proceedings of IEEE the 2001 International Conference on Data Mining(ICDM’01),November 2001:313-320.

[4]X.Yan,J.Han.gSpan:Graph-based Substructure patterns Mining.Proceedings of IEEE the 2002 International Conference on Data Mining(ICDM’02),2002:721-724.

[5]J.Huan,W.Wang,J.Prins.Efficient Mining of Frequent Subgraphs in the Presence of Isomorphism.Proceedings of IEEE the 2002 International Conference on Data Mining(ICDM’03),2003:549-552.

[6]Ray-Yaung Chang, Andy Podgurski,Jiong Yang.Discovering Neglected Conditions in Software by Mining Dependence Graphs,2008,34(5):579-596.