一族新的免求二阶导数的Chebyshev-Halley型迭代法

程桂贤， 何国龙

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

非线性方程求解的方法和理论是当今数值分析研究的重要课题之一，而Newton迭代法是非线性方程求根的重要经典方法［1-2］，其迭代公式为

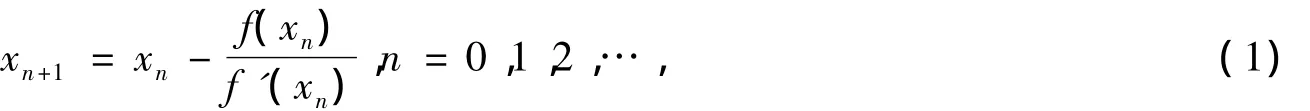
收敛阶为2．

近年来，有不少工作者对Newton迭代法进行了改进［3-6］．如文献［5］中的Newton-Steffensen迭代法，其迭代公式为

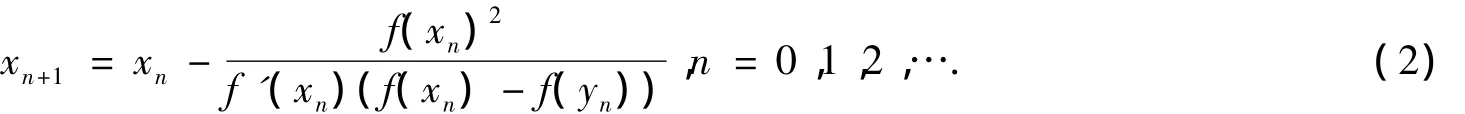
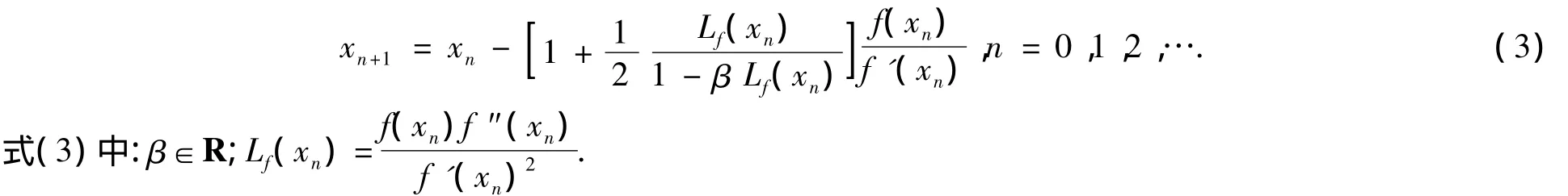
Chebyshev-Halley迭代法是一族收敛阶为3的迭代法，而且一些著名的迭代法包含其中．例如，当法［6-8］．然而，在Chebyshev-Halley迭代法中含有二阶导数的计算．因此，它在实际应用中受到了一定的限制．故求解非线性方程时经常会选用Newton迭代法．

至今，已有许多文献对 Chebyshev迭代法、Halley迭代法及 Chebyshev-Halley迭代法进行了改进［9-13］，其结果优于经典的Chebyshev-Halley迭代法及Newton迭代法．在上述工作的影响下，本文也提出了一族新的免求二阶导数的Chebyshev-Halley型迭代法．在每次迭代过程中只需计算2个函数值和1个一次导数值，其收敛阶仍为3．数值实验结果也验证了此方法的有效性．

1 新的Chebyshev-Halley型迭代法的推导及收敛性分析

设非线性方程

在开区间D⊆R→R上有单根α，且f(x)在D上充分光滑．将f(x)在xn(xn为n次迭代值)处泰勒展开，得

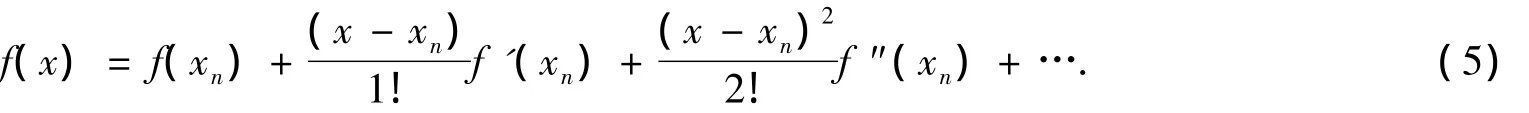
将x=α代入式(5)得

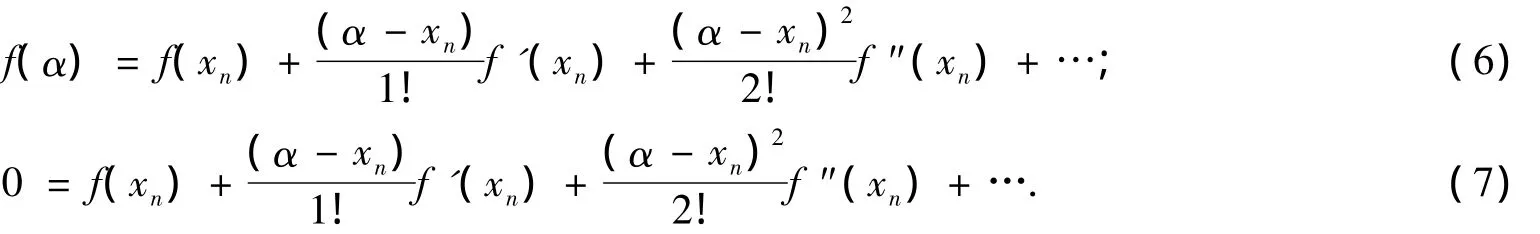
由式(7)可得

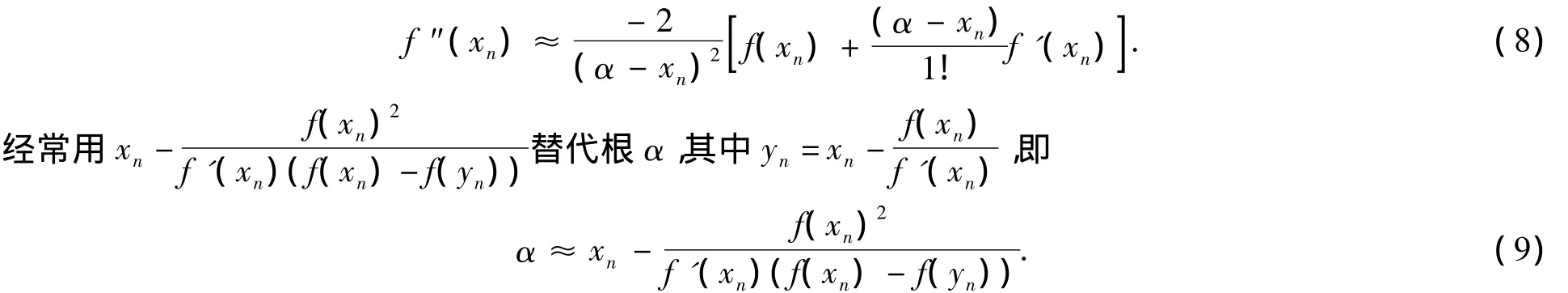
由式(8)和式(9)可得

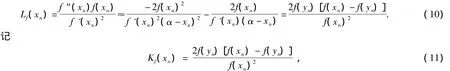
于是，得到一族新的免求二阶导数的Chebyshev-Halley型迭代法

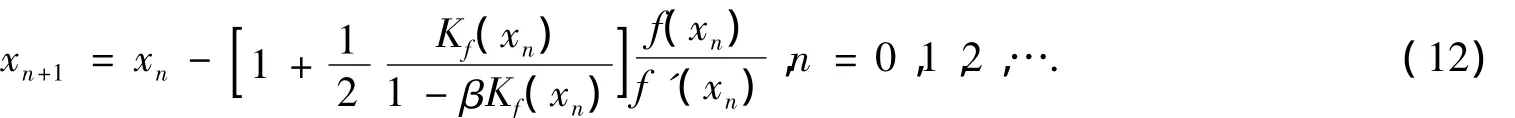
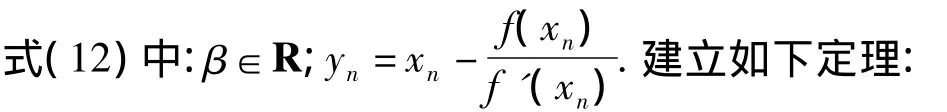
定理1 设f:D⊆R→R在α附近充分光滑，α∈D是方程f(x)=0的单根，且x0充分靠近α，则由式(12)所定义的迭代式的收敛阶至少为3，且误差方程为

证明 将f(xn)，f'(xn)在α处泰勒展开，得

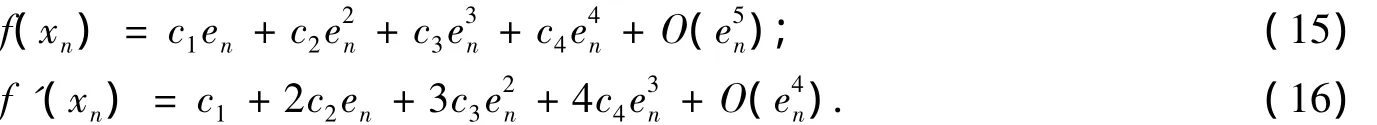
于是

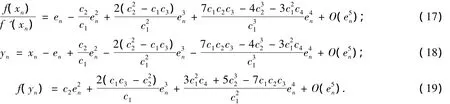
将式(15)及式(19)代入式(11)可得

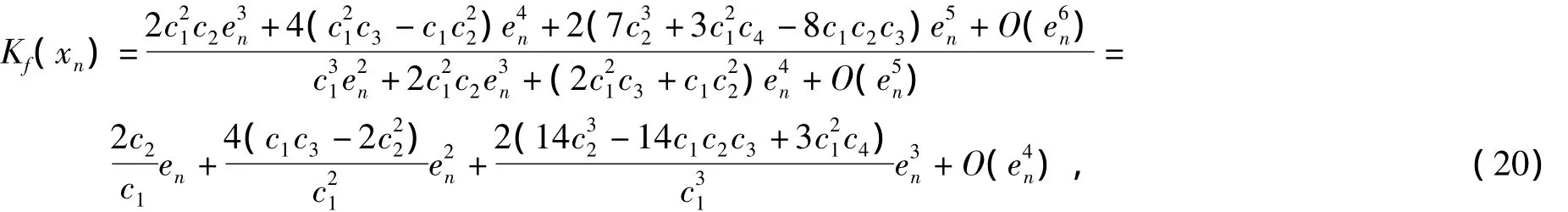
故

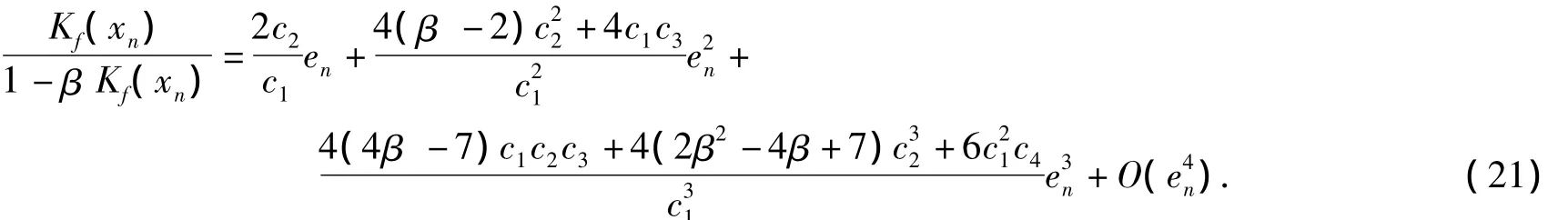
于是1

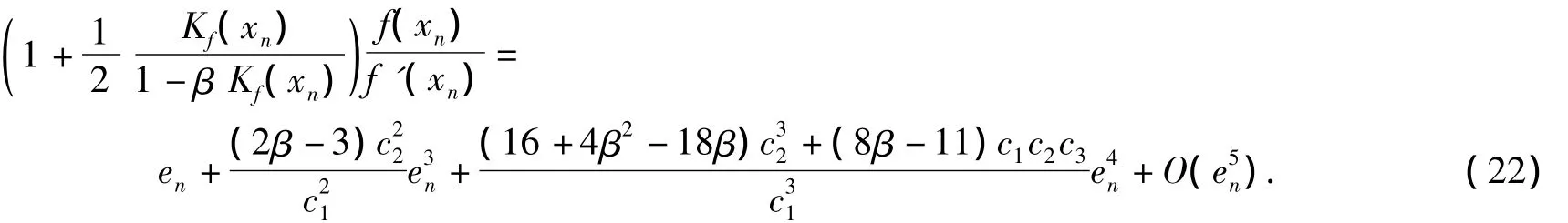
因此

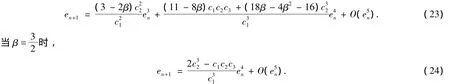
定理1得证．

2 例子

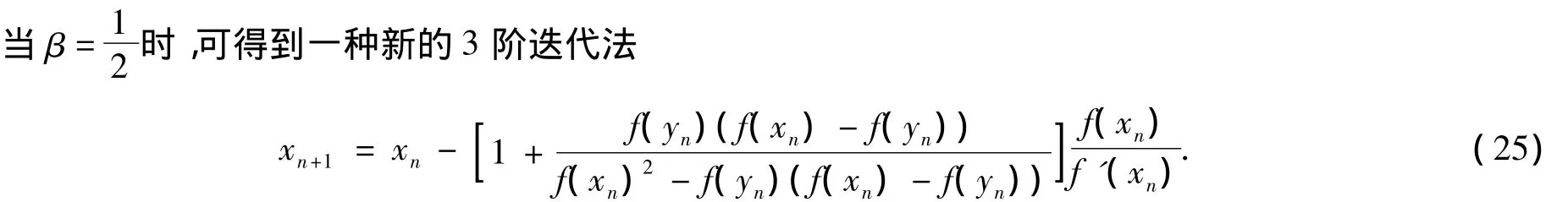
当β=0时，可得到另一种新的3阶迭代法

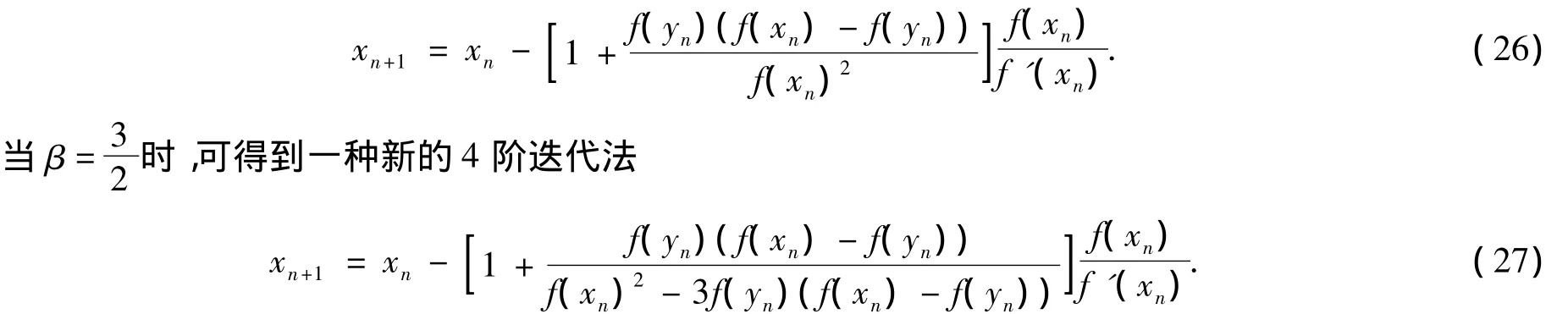
3 数值试验

为了验证本文所给出的迭代法的有效性，对每个算例都用文献［1-2］中的Newton迭代式(NM)、文和本文所给出的迭代式(26)(MCH1)及迭代式(27)(MCH2)进行比较．

给出以下计算实例:

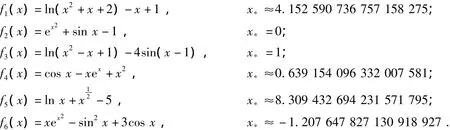
此处x*为方程f(x)=0的根α的近似值，xn为n次迭代后方程f(x)=0的根α的近似值，用TNFE表示函数值的求解总次数，ITN表示迭代次数，COC表示计算的收敛阶的近似值，其计算公式为［14］

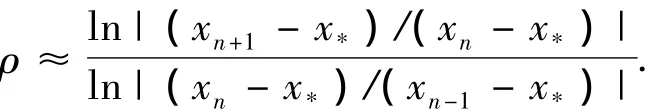
数值计算结果见表1．

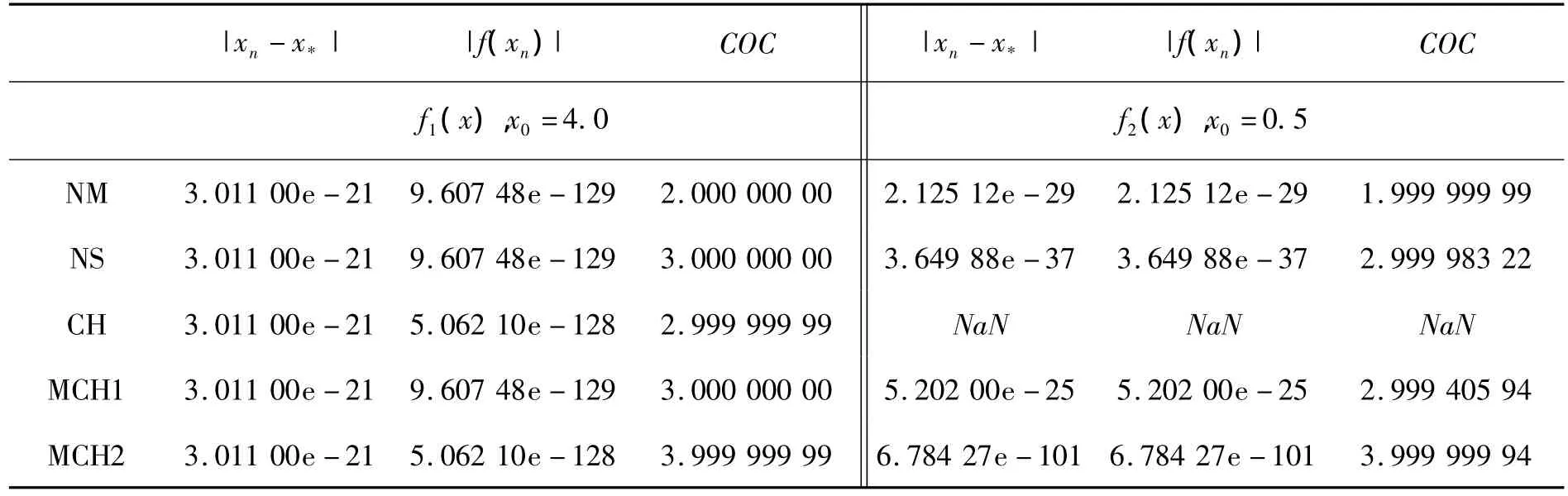
表1 TNFE=12为中止迭代的判定条件

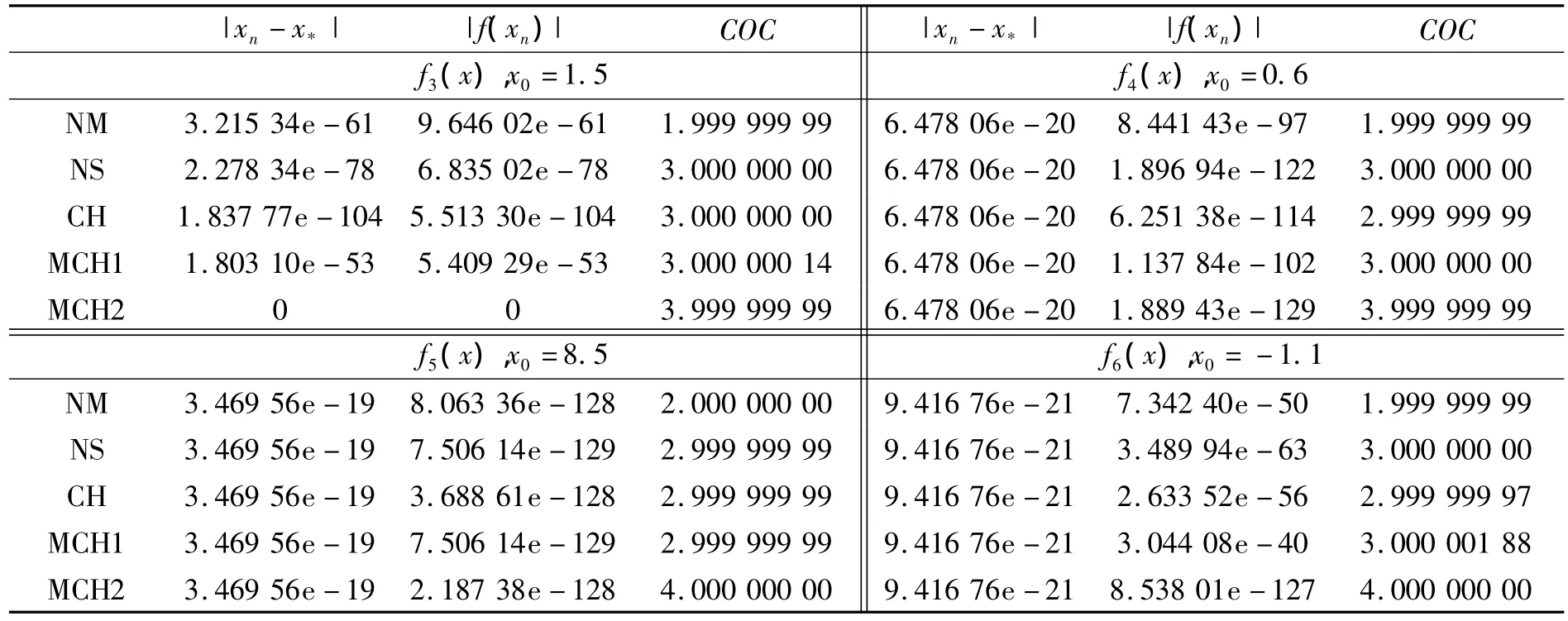
续表1

表2 |xn+1-xn|≤1．0×10-20为中止迭代的判定条件

给出的数值结果说明此方法是有效的．

［1］Ostrowski A M，Rheinboldt W G．Iterative solution of nonlinear equations in several variables［M］．New York:Academic Press，1970．

［2］Traub J F．Iterative methods for the solution of equations［M］．New York:Chelsea Publishing Company，1977．

［3］Amat S，Busquier S，Gutiérrez J M．Geometric constructions of iterative functions to solve nonlinear equations［J］．Computational and Applied Mathematics，2003，157(1):197-205．

［4］Frontiti M，Sormani E．Modified Newton's method with third-order convergence and multiple roots［J］．Computational and Applied Mathematics，2003，156(2):345-354．

［5］Sharma J R．A composite third order Newton-Steffensen method for solving nonlinear equations［J］．Applied Mathematics and Computation，2005，169(1):242-246．

［6］Gutiérrez J M，Hernández M A．A family of Chebyshev-Halley type methods in Banach spaces［J］．Bulletin of the Australian Mathematical Society，1997，55(1):113-130．

［7］Argyros I K．A note on the Halley method in Banach spaces［J］．Applied Mathematics and Computation，1993，58(2/3):215-224．

［8］Gutiérrez J M，Hernández M A．An acceleration of Newton's method:super-Halley method［J］．Applied Mathematics and Computation，2001，117(2):223-239．

［9］Kou J，Li Y，Wang X．Modified Halley's method free from second derivative［J］．Applied Mathematics and Computation，2006，183(1):704-708．

［10］Kou J，Li Y．Modified Chebyshev's method free from second derivative for non-linear equations［J］．Applied Mathematics and Computation，2007，187(2):1027-1032．

［11］Chun C．Some variants of Chebyshev-Halley methods free from second derivative［J］．Applied Mathematics and Computation，2007，191(1):193-198．

［12］Chun C．Some second-derivative-free variants of Chebyshev-Halley methods［J］．Applied Mathematics and Computation，2007，19(2):410-414．

［13］Zhou Xiaojian．Modified Chebyshev-Halley methods free from second derivative［J］．Applied Mathematics and Computation，2008，203(2):824-827．

［14］Weerakoon S，Fernando T G．A variant of Newton's method with accelerated third-order convergence［J］．Applied Mathematics Letters，2000，13(8):87-93．