若干倍图的均匀染色*

傅彩霞

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

本文所考虑的图是简单无向图．对于图G，用V(G)，E(G)，|V(G)|和Δ(G)分别表示G的顶点集、边集、阶和最大度．图G的正常k-染色是指映射f:V(G)→{1，2，…，k}满足∀uv∈E(G)，f(u)≠f(v)．用χ(G)表示G是正常k-可染的最小整数k．在图的染色中，均匀染色是一个重要的染色问题．

定义1 对|V(G)|≥2 的简单图 G(V，E)的正常 k-染色 f，若满足∀i，j∈{1，2，…，k}，||Vi|-|Vj||≤1，则称f为G的一个k-均匀染色．χe(G)表示G是k-均匀可染的最小整数k，称为G的均匀色数．其中Vi={v|v∈V(G)，f(v)=i}，i=1，2，…，k．

1964年，Erdös［1］给出猜想:任何一个图 G 和整数 k≥Δ(G)，G 是(k+1)-均匀可染的．这一猜想于1970 年被 Hajnal和 Szemerédi［2］所证明，即对于图 G，当 k≥Δ(G)+1 时，G 是 k-均匀可染的．在此基础上，Meyer［3］于1973年提出了如下猜想:若连通图G 不为完全图和奇圈，则 χe(G)≤Δ(G)．1994年，Chen等［4］进一步提出了如下猜想:不为Km，C2m+1和K2m+1，2m+1(m≥1)的连通图G 是 Δ(G)-均匀可染的．他们在同一文献中运用换色法等技巧给出了下面3个结论:1)对于Δ(G)≤3的连通图G，G是Δ(G)-均匀3)不为Kn，n的连通二部图G是Δ(G)-均匀可染的．文献［5］证明了Chen等的猜想对外平面图成立，同匀可染的．文献［7］给出了一个漂亮的结果:对于平面图G，若Δ(G)≥13，则G是Δ(G)-均匀可染的．本文讨论了星、扇、轮和棱柱Lm的倍图的均匀染色问题．

定义2［8］对简单图G，G'是G 的拷贝，若V(D(G))=V(G)∪V(G')，E(D(G))=E(G)∪ E(G')∪{uivj|ui∈V(G)，vj∈V(G')且 uiuj∈E(G)}，则称 D(G)为 G 的倍图．

1 星、扇、轮的倍图的均匀色数

本文通过得到某个倍图的均匀色数的下界k，然后给出一个k-均匀染色，从而得到这个倍图的均匀色数．首先给出轮的倍图的均匀色数．

定理1 对n+1阶的轮Wn(n≥3)的倍图D(Wn)，有

证明 记 n+1 阶的轮 Wn(n≥3)为 V(Wn)={ui|i=0，1，2，…，n}，E(Wn)={u0ui|i=1，2，…，n}∪{uiui+1|i=1，2，…，n-1}∪{u1un}．由于 D(Wn)中含 u0的最大独立集为 V0={u0，v0}，故若 f是1．以下分6种情形加以证明．

1)当 n=3 时，由于 D(W3)中含 ui的最大独立集为{ui，vi}(i=0，1，2，3)，因此 χe(D(W3))≥4．下面给出 D(W3)的一个 4-均匀染色．令 f满足 f(ui)=f(vi)=i，i=0，1，2，3，则|Vi|=2，i=0，1，2，3．并且对∀uv∈E(D(W3))，均有 f(u)≠f(v)且||Vi|-|Vj||≤1(i，j∈{0，1，2，3})．所以，f是 D(W3)的一个4-均匀染色，故 χe(D(W3))=4．

2)当 n=4 时，含 u0的最大独立集为{u0，v0}，而{u1，u2，u3，u4，v1，v2，v3，v4}在 D(W4)中的导出子图为K4，4，故V(D(W4))无法划分为4个独立集，使得各个独立集的顶点数相差不超过1，所以不存在D(W4)的 4-均匀染色．下面给出 D(W4)的一个 5-均匀染色．令 f满足 f(ui)=f(vi)=i，i=0，1，2，3，4，则|Vi|=2，i=0，1，2，3，4．并且对∀uv∈E(D(W4))，均有 f(u)≠f(v)且||Vi|-|Vj||≤1(i，j∈{0，1，2，3，4})．所以，f是 D(W4)的一个5-均匀染色，故 χe(D(W4))=5．

3)当n=5时，只需给出D(W5)的一个5-均匀染色．令f满足f(u1)=f(v1)=f(u3)=1，f(u5)=f(v5)=f(v3)=2，f(u4)=f(v4)=3，f(u2)=f(v2)=4，f(u0)=f(v0)=0，则|V1|=|V2|=3;|V3|=|V4|=|V0|=2．并且对∀uv∈E(D(W5))，均有 f(u)≠f(v)且||Vi|-|Vj||≤1(i，j∈{0，1，2，3，4})．所以，f是D(W5)的一个5-均匀染色，故χe(D(W5))=5．

4)当n=3k(k≥2)时，只需给出D(Wn)的=f(uk+i)=f(u2k+i)=i，i=1，2，3，…，k，f(vj)=f(vk+j)=f(v2k+j)=k+j，j=1，2，3，…，k，则|Vi|=3，i=1，2，3，…，2k，|V0|=2．并且对∀uv∈E(D(Wn))，均有 f(u)≠f(v)且||Vi|-|Vj||≤1(i，j∈{0，1，2，

推论1 对n+1阶的扇Fn(n≥2)的倍图D(Fn)，有

1)当 n=2时，χe(D(F2))≥3．令 f满足 f(u1)=f(v1)=1，f(u2)=f(v2)=2，f(u0)=f(v0)=0，则|Vi|=2，i=0，1，2．并且对∀uv∈E(D(F2))，均有 f(u)≠f(v)且||Vi|-|Vj||≤1(i，j∈{0，1，2})．所以，f是D(F2)的一个3-均匀染色，故χe(D(F2))=3．

2)当 n=3时，由定理1知，3≤χe(D(F3))≤χe(D(W3))=4．D(F3)中含 u0的最大独立集为{u0，v0}，含 u2的最大独立集为{u2，v2}，因此，χe(D(F3))≥4，故 χe(D(F3))=4．

3)当 n=4 时，4≤χe(D(F4))≤χe(D(W4))=5．令 f满足 f(u2)=f(v2)=f(u4)=1，f(u3)=f(v3)=f(v1)=2，f(u1)=f(v4)=3，f(u0)=f(v0)=0，则 |V0|=|V3|=2，|V1|=|V2|=3．并且对∀uv∈E(D(F4))，均有 f(u)≠f(v)且||Vi|-|Vj||≤1(i，j∈{0，1，2，3})．所以，f是 D(F4)的一个 4-均匀染色，故 χe(D(F4))=4．

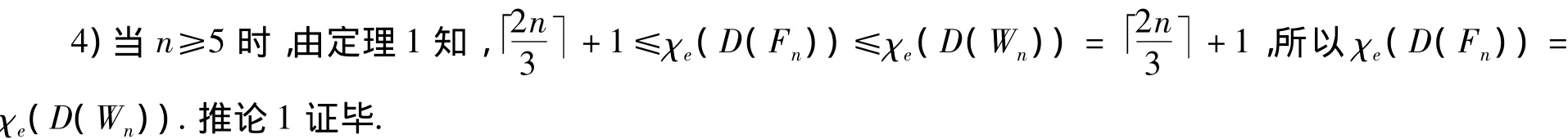
推论2 对n+1阶的星Sn的倍图D(Sn)，有

2 棱柱Lm的倍图的均匀色数

对于简单图 G，u11u12…u1mu11，u21u22…u2mu21是 G 中 2 个不相交的圈，u1i与 u2i(i=1，2，…，m)分别相邻，除此之外没有多余的边，则称G为m-棱柱，记为Lm．

定理2 对Lm(m≥3)的倍图D(Lm)，有

证明 记棱柱 Lm为 V(Lm)={u1i|i=1，2，…，m}∪{u2i|i=1，2，…，m}，E(Lm)={u1iu1i+1|i=1，2，…，m-1}∪{u1mu11}∪{u2iu2i+1|i=1，2，…，m-1}∪{u2mu21}∪{u1iu2i|i=1，2，…，m}．以下对 m 分奇偶进行讨论．

1)m≡1(mod 2)．D(Lm)包含奇圈，所以 χ(D(Lm))≥3，从而 χe(D(Lm))≥χ(D(Lm))≥3．以下分 3种情况进行讨论．

①m≡0(mod 3)．令f满足

结合以上3种情形可得:当m≡1(mod 2)时，χe(D(Lm))=3．

2)m≡0(mod 2)．易知 D(Lm)为二部图，其中 V((D(Lm))=(X，Y;E)的二分划为 X={u1i，u2j，v1i，v2j|i=1，3，5，…，m-1，j=2，4，6，…，m}，Y={u1j，u2i，v1j，v2i|i=1，3，5，…，m-1，j=2，4，6，…，m}，故χe(D(Lm))=2．定理2 证毕．

［1］Erdös P．Extremal problems in graph theory［C］//Miroslav F．Theory of graphs and its applications．NewYork:Prague Pub，1964:29-36．

［2］Hajnal A，Szemeredi E．Proof of a conjecture of Erdös［C］//Erdös P，Renyi A，Sos V T．Combinatorial theory and its applications，VolⅡ．Amsterdam:Bolyai Janos Matematikai Tarsulat，1970:601-603．

［3］Meyer W．Equitable coloring［J］．Amer Math Monthly，1973，80(8):920-922．

［4］Chen B L，Lih K W，Wu P L．Equitable coloring and the maximum degree［J］．European J Combin，1994，15(5):443-447．

［5］Zhang Yi，Yap H P．The equitable Δ-coloring conjecture holds for outerplanar graphs［J］．Bull Inst Math Acad Sinica，1997，25(2):143-149．

［6］Kostochka A V．Equitable coloring of outerplanar graph［J］．Discrete Math，2002，258(1/2/3):373-377．

［7］Zhang Yi，Yap H P．Equitable colorings of outerplanar graph［J］．J Combin Math Combin Comput，1998，27(3):97-105．

［8］Bondy J A，Murty U S R．Graph theory with applications［M］．London:Macmillan，1986．