最大度为6的平面图是13-线性可染的*

王 侃

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

本文所考虑的图都是简单图．用V(G)，E(G)，Δ(G)和δ(G)分别表示图G的顶点集、边集、最大度和最小度．G的围长g(G)是指G中最短圈的长度．

图G的一个正常染色是从顶点集合V(G)到颜色集合{1，2，…，k}的一个映射，使得任意2个相邻的顶点染不同的颜色;图G的一个线性k-染色是一个正常染色，使得染任意2种颜色的顶点集合导出的子图是一些点不交的路的并;图G的线性色数lc(G)定义为G的所有线性k-染色中最小的k值．

Yuster［1］首先研究了图的线性染色问题，证明了任意图G的线性色数满构造了一类图使 实上，这个概念是图的无圈染色的一种特殊情形．图G的一个无圈染色是G的一个正常染色，使得染任意2种颜色的顶点集合导出的子图是一个森林．无圈染色的概念是由Grünbaum［2］提出的，这方面的研究可参阅文献［2-5］．

2008年，Esperet等［6］把线性染色的概念推广到线性选择性上，研究了树、格子图、完全二部图、平面图、外平面图、最大度为3或4的图以及有较小最大平均度的图的线性选择数．文献［6］蕴含了以下结果:若图G满足最大度Δ(G)≤3，则lc(G)≤5;对平面图 G，若 g(G)≥16且Δ(G)≥3，则lc(G)=

文献［7］证明了:对一个平面图 G，若存在一个有序对(Δ，g)∈{(13，7)，(7，9)，(5，11)，(3，13)}Δ(G)≤5，则 lc(G)≤14;对平面图 G，若 Δ(G)≥52，则

本文考虑对平面图类改进上述部分结论，得到如下的结果:

定理1 若G是平面图且满足Δ(G)≤6，则lc(G)≤13．

1 基本概念

对于一个平面图G，用F(G)表示它的面集合．对任意的 f∈F(G)，若u1，u2，…，un是 f边界上依序排列的顶点，则记 f=［u1u2… un］，且点的重复出现是允许的;面的度是指它的边界上边的条数，其中割边被计算2次;对于任意的x∈V(G)∪F(G)，用dG(x)表示G中x的度，在不产生混淆的情况下，可以用d(x)代替dG(x);一个度数为k的顶点(面)被称为k-点(k-面);一个度数至少为k或至多为k的顶点(面)被称为k+-点(k+-面)或k--点(k--面);用NG(v)表示G中v的邻点的集合．

设c是G的一个部分线性染色，颜色集合为C．对于任意的v∈V(G)，用C2(v)表示C中正好在NG(v)上出现2次的颜色子集合;对于任意的顶点集合T，用C*2(T)表示C中至少在T上出现2次的颜色子集合．为讨论方便，称至少关联4个3-面的5-点为坏5-点．

2 极小反例的性质

假设定理1不成立．设G是一个极小反例，即G是一个平面图，满足Δ(G)≤6且lc(G)＞13，但对于任意的一个阶数更小的平面图H，满足Δ(H)≤6，有lc(H)≤13．设C={1，2，…，13}表示被应用的颜色集合．容易看到G是连通的，且G具有以下性质:

断言1 δ(G)≥5．

证明 假设G包含1-点v与某点u相邻．令H=G-v，则H是一个平面图，满足Δ(H)≤Δ(G)≤6．由G的极小性知，H有一个线性染色c应用颜色集合C．为将c扩充到整个图G，用不在C2(u)∪所以总有1种颜色可以染给v．与G的选择矛盾!

假设G包含一个2-点v，其邻点为x，y，则由G的极小性知H=G-v有一个线性染色c应用颜色集合C．用不在{c(x)，c(y)}∪C*2(NH(x)∪NH(y))中的颜色染v，v的禁用颜色数最多为Δ(G)+1=7，于是可用C中的颜色染好v．与G的选择矛盾!

假设G包含一个3-点v，其邻点为x，y，z，则由G的极小性知H=G-v+{xy}(若xy不存在)有一个线性染色c应用颜色集合C．用不在{c(x)，c(y)，c(z)}∪C*2((NG(x)∪NG(y)∪NG(z)){v})中的颜色染v，v的禁用颜色数最多为10，于是可用C中的颜色染好v．与G的选择矛盾!

假设 G 包含一个 4-点 v，且 v1，v2，v3，v4是 v的邻点，则 H=G-v+{v1v2，v3v4}(若 v1v2或 v3v4不存在)(见图1)．由G的极小性知H有一个线性染色c应用颜色集合C．显然，c(v1)≠c(v2)且c(v3)≠c(v4)，考虑3种情形染 v．

1)v1，v2，v3，v4染互不相同的颜色．

用不在{c(v1)，c(v2)，c(v3)，c(v4)}∪ C*2(NG(v1){v})∪C*2(NG(v2){v})∪C*2(NG(v3){v})∪C*2(NG(v4){v})中的中的颜色染好v．

2)v1，v2，v3，v4恰有 1 对顶点染相同的颜色．

不失一般性，设 c(v1)=c(v4)．用不在{c(v1)，c(v2)，c(v3)}∪C*2(NG(v1)∪NG(v4){v})∪C*2(NG(v2){v})∪C*2(NG(v3){v})中的颜色染v，v的禁用颜色数最多为12，于是可用C中的颜色染好v．

3)v1，v2，v3，v4有 2 对顶点染相同的颜色．

不失一般性，设 c(v1)=c(v4)且 c(v2)=c(v3)．用不在{c(v1)，c(v2)}∪C*2(NG(v1)∪NG(v4){v})∪C*2(NG(v2)∪NG(v3){v})中的颜色染v，v的禁用颜色数最多为12，于是可用C中的颜色染好v．断言1证毕．

断言2 不存在坏5-点．

证明 假设G有一个坏5-点v，则v至少和4个3-面关联．设vi(i=1，2，3，4，5)是v的邻点，fi是和v关联的面．设 f1=［v1vv2］，f2=［v2vv3］，f3=［v3vv4］，f4=［v4vv5］．H=G-v+{v2v4，v1v5}(若 v2v4或v1v5不存在)，如图2所示．

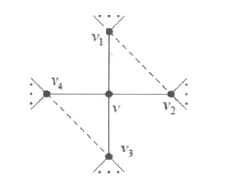
图1 断言1中的子结构

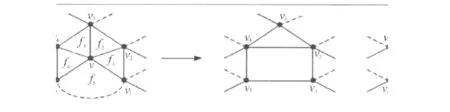
图2 断言2中的子结构

由G的极小性知H有一个线性染色c应用颜色集合C．易见c(v1)≠c(v2)，c(v1)≠c(v5)，c(v4)≠c(v5)，且 c(v2)，c(v3)，c(v4)互不相同．于是在{v1，v2，v3，v4，v5}中至多有 2 个顶点染相同颜色．考虑下面2种情形:

1)c(v1)，c(v2)，c(v3)，c(v4)，c(v5)互不相同．

用不在{c(v1)，c(v2)，c(v3)，c(v4)，c(v5)}，C*2(NG(v1){v，v2})，C*2(NG(v2){v，v1，v3})，C*2(NG(v3){v，v2，v4})，C*2(NG(v4){v，v3，v5})，C*2(NG(v5){v，v4})中的颜色染 v，v 的禁用颜色数最多为12，于是可用C中的颜色染好v．

2)c(v1)，c(v2)，c(v3)，c(v4)，c(v5)中有相同颜色．考虑下面2 种子情形:

①c(v1)=c(v4)或c(v2)=c(v5)．

不失一般性，设 c(v1)=c(v4)．用不在{c(v1)，c(v2)，c(v3)，c(v5)}，C*2((NG(v2){v，v1，v3})∪(NG(v3){v，v2，v4})∪(NG(v5){v，v4}))和 C*2((NG(v1){v，v2})∪(NG(v4){v，v3，v5}))中的颜色染v，v的禁用颜色数至多为12，于是可用C中的颜色染好v．

②c(v1)=c(v3)或c(v3)=c(v5)．

不失一般性，设 c(v1)=c(v3)．用不在{c(v1)，c(v2)，c(v4)，c(v5)}，C*2((NG(v2){v，v1，v3})∪(NG(v4){v，v3，v5})∪(NG(v5){v，v4}))和 C*2((NG(v1){v，v2})∪(NG(v3){v，v2，v4}))中的颜色染v，v的禁用颜色数至多为12，于是可用C中的颜色染好v．断言2证毕．

3 定理1的证明

设G是定理1的一个极小反例，为完成证明，应用权转移方法．首先，结合欧拉公式|V(G)|-

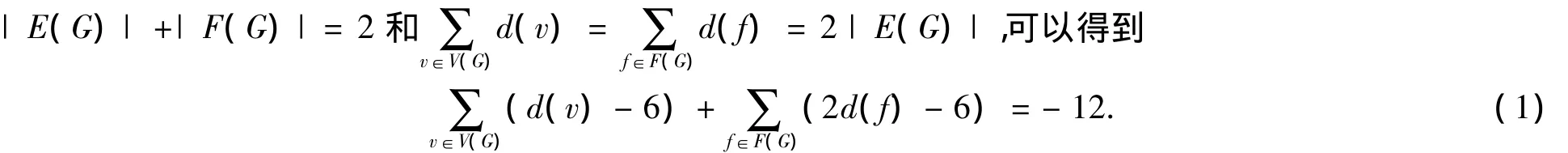
定义初始权函数w:对v∈V(G)，令 w(v)=d(v)-6;对 f∈F(G)，令 w(f)=2d(f)-6．由式(1)得总的权和为-12．然后定义一个权转移规则并且在所有的点和面上执行它．一旦权转移结束，就会产生一个新的权函数w'．在整个权转移过程中权和是不变的，但是对于所有的x∈V(G)∪F(G)，有w'(x)≥0．这就导致了下面一个很明显的矛盾:

因此，这样的反例G是不存在的．

权转移规则如下:

［1］Yuster R．Linear coloring of graphs［J］．Discrete Math，1998，185(1/2/3):293-297．

［2］Grünbaum B．Acyclic colorings of planar graphs［J］．Israel J Math，1973，14(4):390-408．

［3］Borodin O V．On acyclic colorings of planar graphs［J］．Discrete Math，1979，25(3):211-236．

［4］Kostochka A V．Acyclic 6-coloring of planar graphs［J］．Metody Diskret Anal，1976，28:40-56．

［5］Wang Weifan，Shu Qiaojun，Wang Kan，et al．Acyclic chromatic indices of planar graphs with large girth［J］．Discrete Appl Math，2011，159(12):1239-1253．

［6］Esperet L，Montassier M，Raspaud A．Linear choosability of graphs［J］．Discrete Math，2008，308(17):3938-3950．

［7］Raspaud A，Wang Weifan．Linear coloring of planar graphs with large girth［J］．Discrete Math，2009，309(18):5678-5686．

［8］王侃．不含3-圈平面图的线性染色［J］．浙江师范大学学报:自然科学版，2011，34(2):135-140．

［9］Li Chao，Wang Weifan，Raspaud A．Upper bounds on the linear chromatic number of graph［J］．Discrete Math，2011，311(4):232-238．