基于α稳定分布的地震反演方法

岳碧波，彭真明，张启衡

1电子科技大学光电信息学院，成都 610054 2中国科学院光电技术研究所，成都 610209

基于α稳定分布的地震反演方法

岳碧波1，彭真明1，张启衡2

1电子科技大学光电信息学院，成都 610054 2中国科学院光电技术研究所，成都 610209

本文介绍了α稳定分布的统计特征，并对比分析了实际地震信号与α稳定分布的动态样本方差特征，提出地震信号服从非高斯α稳定分布的假设．在此基础上，利用地震记录估计误差的p阶统计量作为代价函数，提出了基于非高斯α稳定分布的最小p范数地震反演方法．将该方法应用到单道反射系数理论模型及实际叠前弹性阻抗反演实例中，均取得了良好的反演效果．实际反演结果验证了本文提出的地震信号服从非高斯α稳定分布假设的合理性，以及最小p范数地震反演方法的可行性和有效性．

α稳定分布，非高斯，反演，p范数

1 引 言

地震反演是地球物理勘探中的核心内容之一，其目的是根据地表观测信号推测地球内部与信号有关的物理状态．经过近三十年的发展，地震反演方法的研究已经得到了很大的进步，尤其是近些年出现了许多优秀的非线性反演方法，例如，模拟退火反演方法、神经网络反演方法以及粒子群反演方法［1］等．这些方法都是假定地震信号是服从高斯分布的，但是事实上地震信号并非服从高斯分布，例如Walden［2］研究反射系数的幅度分布特点，提出反射系数序列是非高斯分布的．对于非高斯反演方法，彭真明等［3］提出了粒子滤波的AVO反演方法，同时指出该反演方法可以用于非高斯地震反演中；Liu等［4］研究了非高斯性最大化的预测反演方法．但是这些方法都没有指出地震数据的具体统计分布．陈建江［5］将Cauchy分布作为反射系数的先验分布，研究了AVO三参数反演方法．反射系数是否服从Cauchy一般很难确定，Godfrey［6］认为广义高斯分布在某种情形下比Cauchy更符合反射系数的分布特征．因此，对于地震信号究竟服从何种统计分布，仍然是值得当前学术界探讨的话题．

α稳定分布是一种满足广义中心极限定理的稳定分布，与高斯分布相比，该分布有较厚拖尾，符合地震信号的实际分布特征．另外，该分布在参数取特定值时会退化为高斯（Gaussian）分布、柯西（Gauchy）分布以及列维（Lévy）分布等特殊分布形式．因此，α稳定分布是一种比高斯分布适用性更广的随机概率分布．目前基于α稳定分布的信号处理方法已经在通信信号去噪［7］、图像处理［8］、目标检测［9］等领域得到了广泛的关注和深入的研究．

本文将非高斯α稳定分布作为地震数据的统计分布，并提出一种基于非高斯α稳定分布的最小p范数地震反演方法．本文第2部分论述α稳定分布的基本统计特性，并探讨了利用数据的动态样本方差判定数据是否是服从高斯分布的方法，以及基于非高斯α稳定分布信号的分数低阶矩处理方法；第3部分分析实际地震数据的动态样本方差特征，相比于高斯分布，这些地震数据的动态样本方差曲线更接近于非高斯α稳定分布数据的动态样本方差曲线；第4部分以叠前弹性阻抗反演为例，提出了基于非高斯α稳定分布的阻抗反演方法；第5部分将最小p范数地震反演方法应用到实际叠前弹性阻抗反演中．反演结果表明本文提出的地震信号服从非高斯α稳定分布的假设是合理的，同时也表明了最小p范数地震反演方法的有效性和可行性．

2 α稳定分布理论

α稳定分布是一种比高斯分布适用性更广的统计分布，高斯分布只是α稳定分布的一个特例．该分布是从广义中心极限定理发展而来的一类极限分布，这类分布没有封闭的概率密度函数表达式，其统计特性通常由特征函数来描述．对于一个服从α稳定分布的随机变量X，其特征函数的表达式为

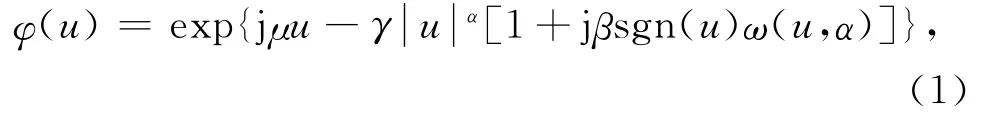
式中

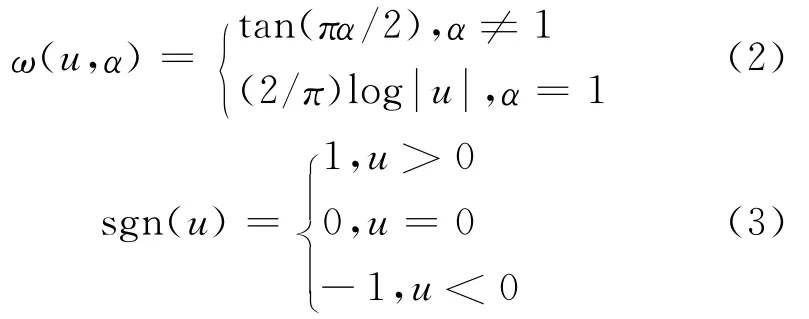
其中α、β、γ和μ是α稳定分布的四个分布参数．α（0＜α≤2）为α稳定分布的特征指数，该参数的大小决定了α稳定分布的拖尾厚度，其取值越小，分布的拖尾越厚；β（－1≤β≤1）为对称参数，决定分布的倾斜度，当β＝0时，α稳定分布的概率密度函数是关于u对称的；γ（γ＞0）表示分布的分散程度；μ（－∞＜μ＜∞）对应于分布的位置参数．

2．1 α稳定分布的三个特例

α稳定分布的统计特性由参数（α，β，γ，μ）决定，当参数取特定值，α稳定分布可退化为以下的三种特例形式：

（1）当α＝2，β＝0和γ＝σ2／2时，α稳定分布退化为高斯分布，此时的随机变量X～N（μ，σ2）；

（2）当α＝1，β＝0和γ＝σ时，α稳定分布退化为柯西分布；

（3）当α＝1／2和β＝1时，α稳定分布退化为列维分布，概率密度函数在区间x∈（μ，＋∞）上收敛．

2．2 非高斯α稳定分布的判定

服从非高斯α分布随机数据与服从高斯分布随机数据最大的不同之处在于，前者具有更强的脉冲特性，即概率密度函数具有厚拖尾现象．由于脉冲特性的存在，服从非高斯α稳定分布的数据的二阶矩不收敛，也没有有限的二阶以上的高阶矩，而高斯分布有稳定的二阶矩以及有限的高阶矩．因此，判定获得的观测数据是否服从非高斯α稳定分布，一个简单有效的办法就是考察观测数据的样本方差是否收敛．如果一组数据的样本方差不收敛，则该组数据一定不是高斯分布数据．

设观测数据X1，X2，…，XN为同分布随机序列，对每一个1≤n≤N，前n个观测数据的动态样本方差为［10］

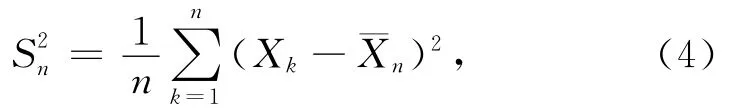
其中

为了验证高斯分布数据与非高斯α稳定分布数据的动态样本方差的不同，以及参数α对非高斯α稳定分布脉冲特征的影响，本文产生了三组随机数据，其中第一组为高斯分布随机数据，第二组为参数为（1．6，0，1，0）的α稳定分布随机数据，第三组为参数为（1．4，0，1，0）的α稳定分布随机数据，分别如图1a、图2a和图3a所示，三组随机数据长度均为2×104．图1b、图2b和图3b分别为图1a、图2a和图3a中对应随机数据的动态样本方差．

图1 高斯分布随机数据（a）及其动态样本方差（b）Fig．1 （a）Gaussian random data and（b）its dynamic sample variance

图2 参数为（1．6，0，1，0）的α稳定分布随机数据（a）及其动态样本方差（b）Fig．2 （a）α－stable distribution random data for（1．6，0，1，0）and（b）its dynamic sample variance

图3 参数为（1．4，0，1，0）的α稳定分布随机数据（a）及其动态样本方差（b）Fig．3 （a）α－stable distribution random data for（1．4，0，1，0）and（b）its dynamic sample variance

对比图1a、图2a和图3a可见，随着α稳定分布的参数α取值的减小，随机数据的脉冲特性加强．其中图1a中的服从高斯分布（α＝2时的α稳定分布）的随机数据起伏很稳定，脉冲性很弱，数据的动态样本方差随着样本点数的增加很快地收敛于一个稳定值，如图1b所示；图2a中特征参数减小为α＝1．6，产生的随机数据的脉冲特性相对于图1a中的高斯随机数据明显增强，该组随机数据对应的动态样本方差曲线如图2b所示，由图可见，随着样本点数的增加随机数据的动态样本方差呈台阶状递增，而不趋于一个稳定值；在图3a中，取特征参数α＝1．4，脉冲特性变得更明显，脉冲点的能量更强，其动态样本方差如图3b所示，数据对应的动态样本方差急剧跳跃到很大值．

2．3 非高斯α稳定分布信号处理

在对信号进行处理的时候，通常认为数据是服从高斯分布的．对于服从高斯分布的数据，采用基于二阶矩的算法就可以对数据进行处理．但是对于服从非高斯α稳定分布的数据，由于其没有有限的二阶矩以及二阶以上的高阶矩，因此，对非高斯的α稳定分布数据，只能在低于二阶的分数低阶矩下处理，通常称为p（0＜p＜α≤2）阶矩．一维α稳定分布随机变量X的p阶矩为

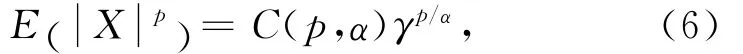
其中，

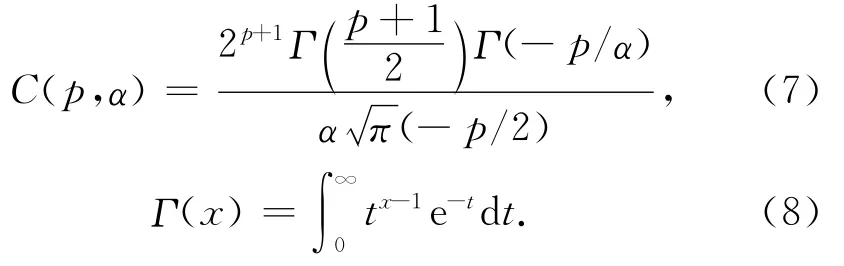
对于非高斯α稳定分布随机变量X，假设它的分散系数为γ，当1≤α≤2时，它张成的空间为Banach空间．将随机变量X的范数定义为

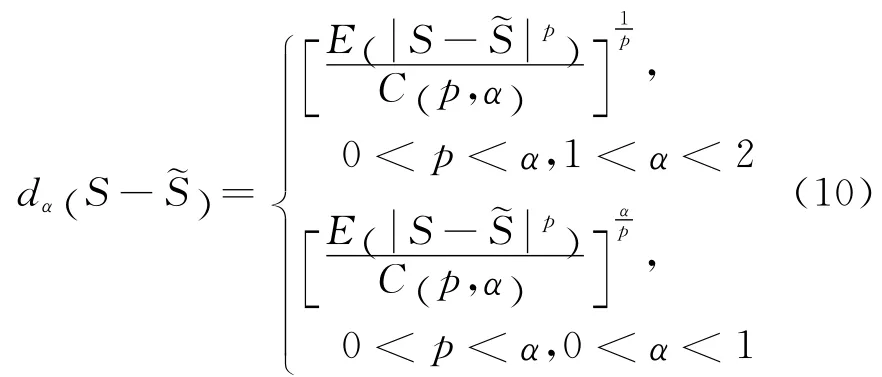
3 地震数据的非高斯分布分析

对于服从不同分布的信号，在处理时采用的手段是有很大差别的，因此对数据分布的正确判断很重要．在本文前面已经介绍了非高斯α稳定分布与高斯分布数据的脉冲特性，服从非高斯α稳定分布的数据的动态样本方差是不收敛的．根据数据的动态样本方差的特征，我们可以大致判断要处理的数据是服从高斯分布还是服从非高斯α稳定分布的．

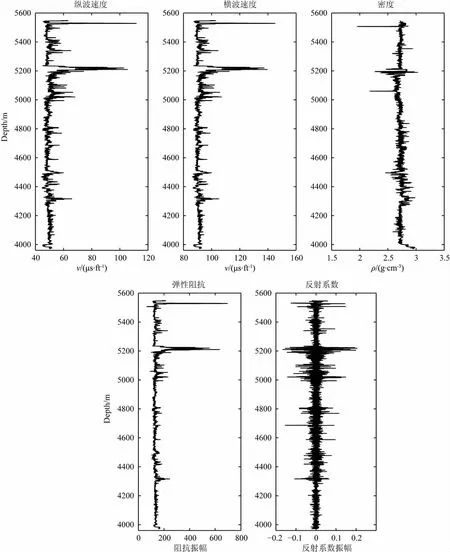
本文选取川东北地区某区块X6测井处的地震数据作为例子分析实际地震数据的统计分布情况．图4所示为该区块入射角度为3°时X6井旁道地震记录以及对应的动态样本方差，该角度地震记录的有效数据段为500ms到3640ms，采样时间为2 ms．图5为该区块X6井处的测井数据（包括纵波速度、横波速度、密度）以及相对应的阻抗、反射系数，数据对应的深度范围为3971．75～5548．25m，采样间隔为0．25m．再对这组测井数据分别计算动态样本方差，如图6所示．其中图6a中实线为纵波阻抗对应的动态样本方差，点划线为横波阻抗对应的动态样本方差；图6b为密度的动态样本方差；图6c为测井阻抗对应的动态样本方差；图6d为测井反射系数对应的动态样本方差．

由图4中所示井旁道地震记录对应的动态样本方差曲线可见，地震数据的动态样本方差随着数据样本点数的增加并没有趋于稳定，而是呈阶梯状上升．并且，由图6中的各组曲线可以看出，纵、横波速度对应的动态样本方差也是呈阶梯状上升的，虽然密度对应的动态样本方差曲线最后处于相对稳定的状态，但是由密度以及纵、横波速度获得的阻抗和反射系数所对应的动态样本方差都呈现阶梯状上升，并不趋于一个稳定值．将图4和图6分别与图1b、图2b和图3b相比，可见实际的地震数据的动态样本方差曲线的变化趋势更加接近于非高斯α稳定分布数据的动态样本方差，而与高斯分布数据的动态样本方差差异很大．因此，将实际的地震数据的分布假设为非高斯α稳定分布比假设其为高斯分布更为合理．

图4 入射角度为3°时的井旁道地震记录（a）及其动态样本方差（b）Fig．4 （a）Seismic trace and（b）its dynamic sample variance with incidence angle of 3°

4 叠前地震反演过程

4．1 弹性阻抗反演原理

叠前反演是以Zoeppritz方程为基础的，在Zoeppritz方程的基础上，人们又提出了很多的近似方程，其中Shuey［11］近似方程使用最为广泛．

基本弹性阻抗的表达式为

式中，α为纵波速度，β为横波速度，ρ为密度，θ为纵波入射角，参数K＝［（βi／αi）2－（βi＋1／αi＋1）2］／2代表纵横波速度比的平均值．

当入射角θ很小时，有sin2θ≈tan2θ，于是基本弹性阻抗表达式（11）可以表示为

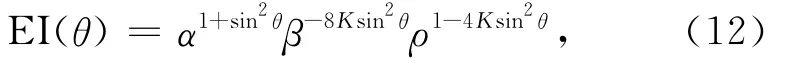
在式（12）中，令a＝1＋sin2θ，b＝－8 Ksin2θ，c＝1－4 Ksin2θ，则式（12）可以更简单地表示为

应该区分病理性黄疸和母乳性黄疸。病理性的主要是新生儿溶血（黄疸在出生24小时内出现尤其要注意）、肝炎和肠梗阻等。母乳性黄疸不要紧，可以吃点益生菌（金双歧或培菲康）。中药用茵栀黄口服液或颗粒剂，药店没有出售，可以请医生开。

4．2 非高斯α稳定分布下的EI反演

对于服从非高斯α稳定分布的数据，只能在分数低阶矩下处理［12－16］，国内有的学者将其称为p范数方法［17］．由式（10）可知，在对服从α稳定分布的信号进行估计时，如果估计信号~S与真实信号S之间的距离dα（~S－S）达到最小，即认为此时的估计信号~S最优．因此，对于满足非高斯α稳定分布的地震记录，只要地震记录的估计与实际的地震记录的距离dα－S）达到最小，即估计误差的p阶统计量最小时，地震记录对应的弹性阻抗就是最优的．

令入射角度为θ时某道的地震记录为S（θ），反射系数为R（θ），对应的子波为W（θ），则

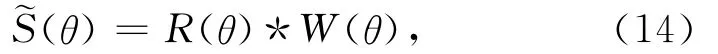
其中，符号＊代表褶积运算，~S（θ）为实际的地震记录S（θ）的估计值．

式（14）用矩阵的形式表示为

图6 X6井处测井数据对应的动态样本方差Fig．6 Dynamic sample variance of log data of well X6

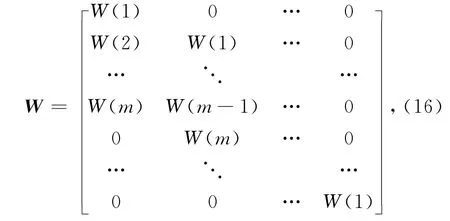
矩阵中的W（i）为子波W（θ）的第i个采样值，其中1≤i≤m，m为子波总的采样点数．

令地震记录采样后的向量为S＝［s（1），s（2），…，s（M）］T，真实地震记录与其估计之间的误差向量为

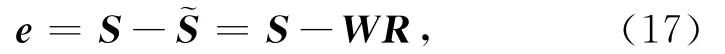
以式（17）所示的估计误差的p（1＜p＜α≤2）阶统计量建立代价函数．定义代价函数为

当代价函数J在误差的p统计量下取得最小值时，所对应的反射系数即为最优解．这样，反演问题转化成了求解式（18）的最小值的数学问题．代价函数是关于反射系数的函数，对代价函数求梯度，可得

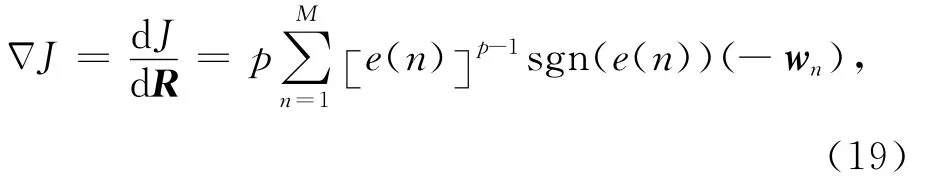
式（19）中e（n）表示误差向量e的第n个元素，wn为子波矩阵W的第n行．

根据最速下降Δ算法，可得关于反射系数的递推式

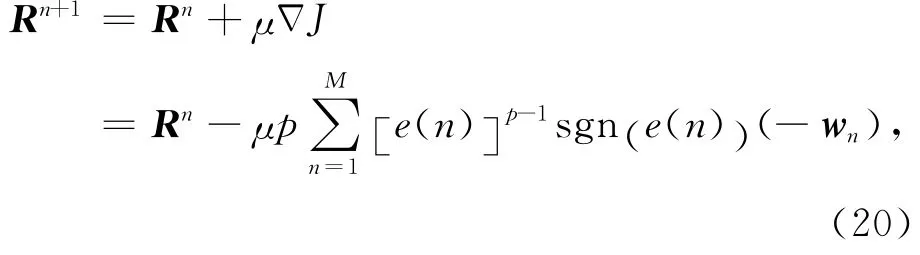
其中，μ＞0，为自动调整步长．利用迭代的方法很容易得到反演结果．该算法称为最小p范数反演方法．

设定初始模型反射系数为R0，最大误差为e（e＞0），最大迭代次数Itera．利用迭代的方法实现最小p范数反演方法的步骤为

步骤1，初始化，R（0）＝R0；

步骤4，由式（20）更新反演结果，若迭代次数n＋1＝Itera，转步骤5，否则转步骤2；

步骤5，输出反射系数R（n）．

在迭代过程中，自动调整步长μ的选取对最后的反演结果将产生影响，μ取值小可以减小稳态失调量，提高算法的精度，但是会影响算法的收敛速度；μ取值大可以提高算法的收敛速度，但是会影响算法的精度．因此，自动调整步长μ的取值应视应用环境而定．地震反演属于非实时信号处理，在算法的速度要求不高的情况下，设置μ为小值将有利于反演结果精度的提高．

5 反演实例与分析

5．1 理论模型反演

将本文研究的基于非高斯α稳定分布假设的反演方法应用到实际的地震资料中，地震数据来自川东北地区某区块，数据已经过叠前时间偏移和动校正（NMO）处理，地震数据的采样率为2ms．利用该区X6井目的层段的测井数据计算反射系数如图7a所示，数据对应的地震剖面时间为1800～2300ms；图7b为以中心频率为45Hz，长度为100ms的雷克子波，子波的最大振幅已根据测井的阻抗值幅度做了校正；图7c为图7a中的反射系数与图7b中所示的子波卷积得到的合成地震记录．

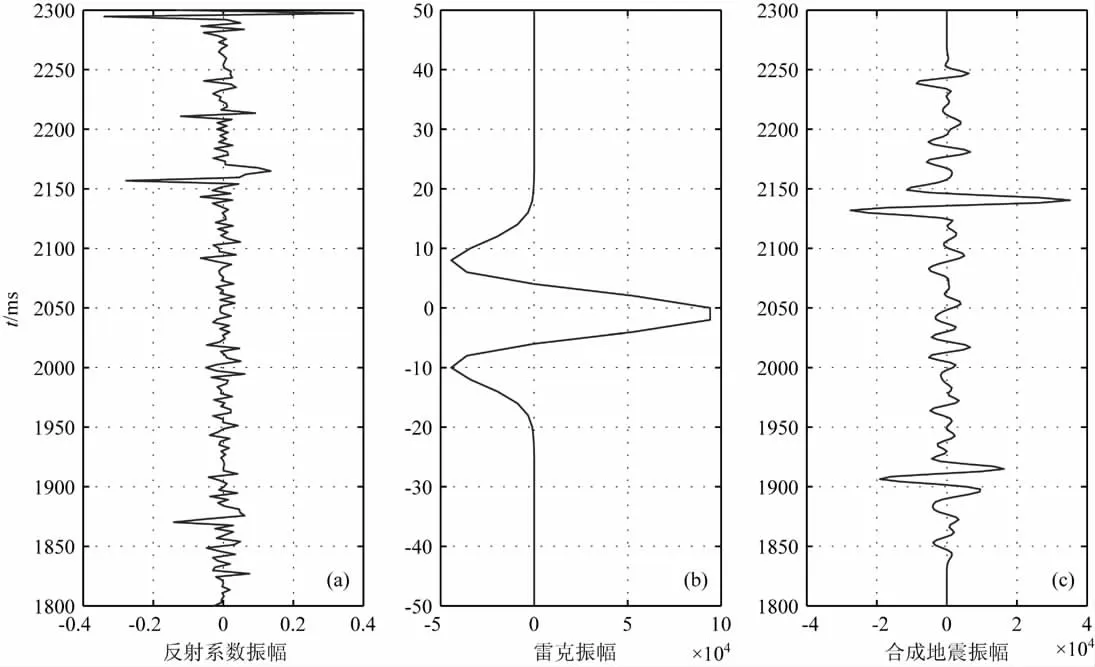
图7 理论模型及合成地震记录Fig．7 Reflectivity and wavelet model and synthetic seismogram

为了验证最小p范数反演方法的可行性，将最小p范数反演方法获得的反演结果与基于高斯分布二阶矩的最速下降算法反演结果比较．本文利用图7中所示的数据做理论的试算，从图7c所示的合成地震记录和图7b所示的雷克子波出发，分别用上述的两种反演方法各获得一组反演结果．反演结果如图8b所示，其中红色实线REF1为利用最小p范数反演方法，即利用式（20）反演出的反射系数序列，蓝色的点划线REF2为利用基于高斯分布二阶矩的最速下降算法反演出的反射系数．两种方法中，自动调整步长均为μ＝0．82，基于最小p范数反演方法中取误差范数为p＝1．92．图8a为实际的测井处的反射系数，与图7a中所示的是同一个数据；图8c为实际的反射系数与反演出的反射系数的误差序列，其中的红色实线ERR1为实际的反射系数与REF1的误差，蓝色的点划线ERR2为实际的反射系数与REF2的误差．从图8a和图8b看出，反演出的反射系数与实际的反射系数在波形的趋势上吻合度非常高；而且图8c中的误差曲线表明了，除少数点外，绝大部分误差都小于0．02．另外，图8c中误差曲线ERR1在反射系数峰值处（例如，2200ms附近）的起伏明显低于ERR2．这是因为反射系数是服从非高斯α稳定分布的，在峰值处处在脉冲现象，在这种情况下，基于非高斯α稳定分布的最小p范数反演方法的性能优于基于高斯分布的二阶矩方法．

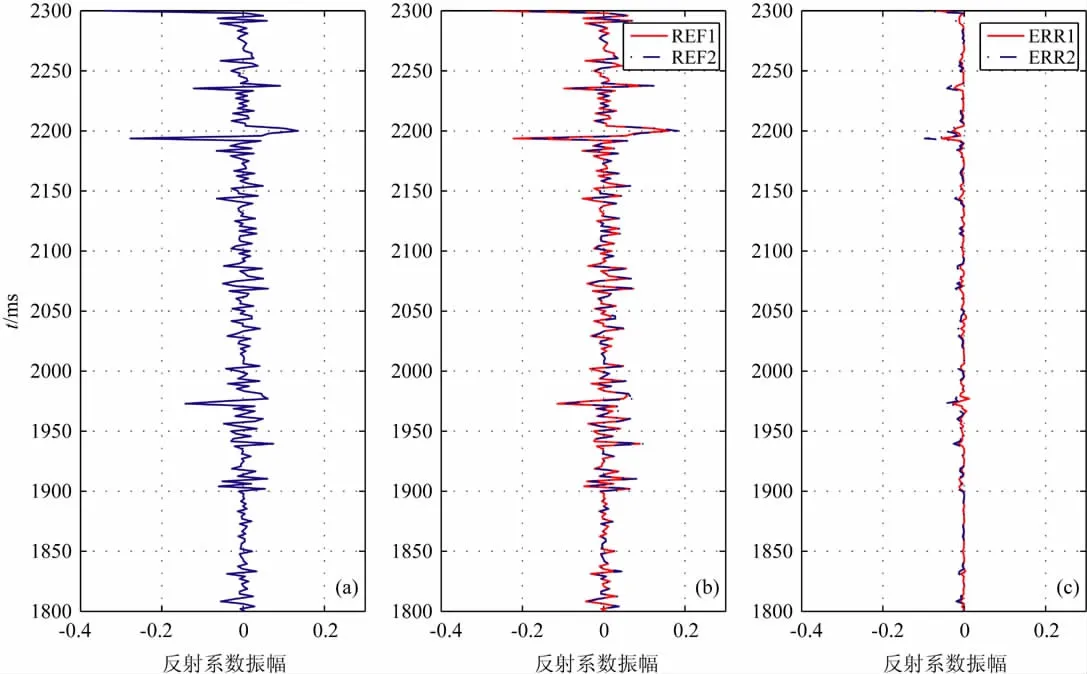
图8 原始反射系数（a）、反演结果（b）及其误差（c）Fig．8 （a）Original reflectivity，（b）inversion results and（c）estimation errors

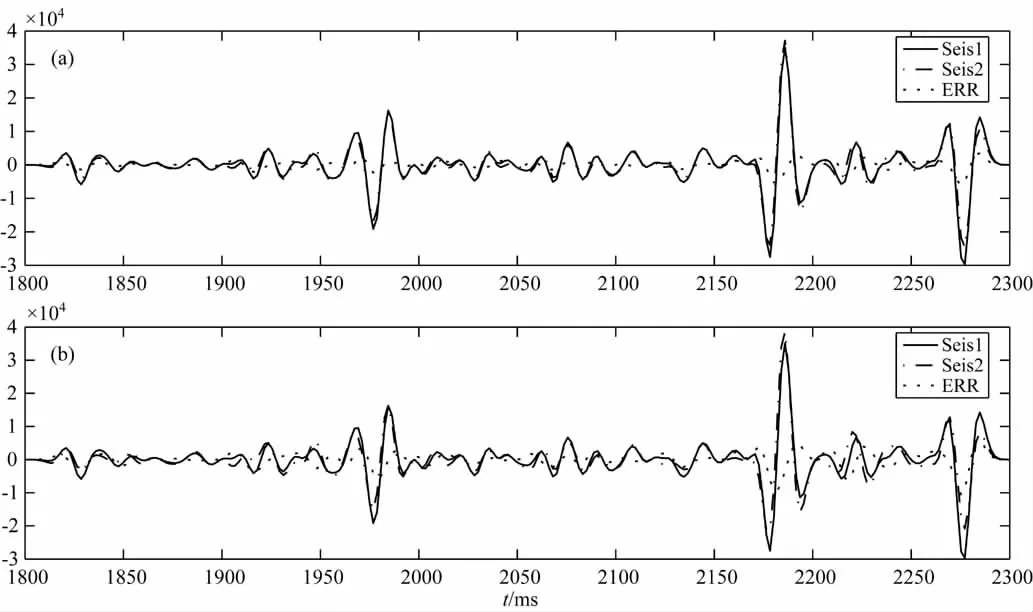
图9 地震记录比较Fig．9 Comparison between original synthetic and synthetics calculated from inverted results

再将两种方法反演得到的反射系数（如图8b所示）分别与雷克子波（如图7b所示）卷积，得到地震记录估计．将该地震记录的估计与图7c中的原始地震记录在同一图中显示，如图9所示．其中图9a中的实线Seis1为原始的地震记录，点划线为图8b中REF1与子波卷积得到的地震记录估计，划线ERR为原始地震记录与地震记录估计的误差曲线；图9b中的实线Seis1为原始的地震记录，点划线为图8b中REF 2与子波卷积得到的地震记录估计，划线ERR为原始地震记录与地震记录估计的误差曲线．由图9a可见，曲线Seis1与曲线Seis2吻合度非常高，误差曲线Err起伏很小．同时，比较图9a中的曲线Seis2与图9b中的曲线Seis2，不难发现，图9a中的Seis2曲线在地震记录的大峰值处（如，2180ms和2275ms处）与原始的地震记录的吻合度明显要高于图9b中Seis2与原始地震记录的吻合度．从图8和图9这两组图可以得出结论，基于α稳定分布的最小p范数反演方法是可行的．

5．2 叠前弹性阻抗反演

通过以上的理论模型反演，验证了基于α稳定分布的最小p范数反演方法的可行性．本文再将该反演方法应用到整个区块的叠前弹性阻抗反演中．选取误差范数为p＝1．92，自动调整步长μ＝0．82，分别反演得到3°、9°和15°三个入射角下过X6井的某测线的叠前弹性阻抗剖面，如图10a、图10c和图10e所示．将图中红色椭圆标记处放大，如图右上角所示，阻抗呈现低值（蓝色）．因此，可初步判断标记区域为储层位置，这与测井解释该区域层为含气、水层的结果是吻合的．

图10 多角度弹性阻抗反演结果Fig．10 Maps of multi－angle elastic impedance obtained by the least p－norm inversion algorithm

彭真明等［18］研究了流体信息与不同角度弹性阻抗的关系，得出结论，随着入射角度的增加，含气储层阻抗值会减小．随着图10a、图10c和图10e中对应入射角度逐渐增加，在预测的储层处（红色椭圆标记处）阻抗值随入射角度增加而减小，变化规律与彭真明等人得到的结论吻合．

图10b、图10d和图10f分别为图10a、图10c和图10e标记处附近的阻抗波形图．波形图显示的CDP范围为310～350，时间范围为1900～2240ms，红色曲线为测井处阻抗．由这三组波形图可见，反演结果与实际测井数据吻合度非常高．充分说明了本文研究的基于α稳定分布的最小p范数反演方法在地震反演中的有效性．

6 结 论

α稳定分布是一种比高斯分布适用性更广的概率分布．本文通过对地震信号的动态样本方差分析表明，地震数据的分布更接近于非高斯的α稳定分布，而不是传统的高斯分布．由于非高斯α稳定分布的二阶统计量不存在，若仍按照传统的高斯分布假设下的地震反演方法，选取地震记录估计误差的二阶矩作为代价函数，反演结果不是最优的．因此，在对非高斯的α稳定分布的地震信号反演时必须取地震记录估计误差的p（1＜p＜α）阶统计量作为代价函数．

通过对川东北地区某区块X6井反射系数的对比反演，验证了本文提出的反演方法的可行性．最后将该反演方法应用到该区块多角度叠前弹性阻抗反演中，取得了很好的效果．这一成功的应用不仅表明了实际的地震信号是服从非高斯α稳定分布的，而且证实了利用非高斯α稳定分布的方法进行地震反演的有效性．

（References）

［1］ 岳碧波，彭真明，洪余刚等．基于粒子群优化算法的叠前角道集子波反演．地球物理学报，2009，52（12）：3116－3123．Yue B B，Peng Z M，Hong Y G，et al．Wavelet inversion of pre－stack seismic angle－gather based on particle swarm optimization algorithm．Chinese J．Geophys．（in Chinese），2009，52（12）：3116－3123．

［2］ Walden A T．Non－Gaussian reflectivity，entropy，and deconvolution．Geophysics，1985，50（12）：2862－2888．

［3］ 彭真明，李亚林，魏文阁等．粒子滤波非线性AVO反演方法．地球物理学报，2008，51（4）：1218－1225．Peng Z M，Li Y L，Wei W G，et al．Nonlinear AVO inversion using particle filter．Chinese J．Geophys．（in Chinese），2008，51（4）：1218－1225．

［4］ Liu J，Lu W K．An improved predictive deconvolution based on maximization of non－Gaussianity．Applied Geophysics，2008，5（3）：189－196．

［5］ 陈建江．AVO三参数反演方法研究［博士论文］．山东：中国石油大学，2007．Chen J J．Study of three－term AVO inversion method［Ph．D．thesis］（in Chinese）．Shandong：China University of Petroleum，2007．

［6］ Godfrey B，Claerbout J F．Two methods of deconvolution：power spectrum smoothing and parsimonious deconvolution．Stanford Exploration Project，1978，14：207－226．

［7］ 孙永梅，邱天爽．α稳定分布噪声下自适应信号处理的研究进展．信号处理，2004，20（6）：618－622．Sun Y M，Qiu T S．The development of adaptive signal processing in alpha－stable noise environments．SignalProcessing（in Chinese），2004，20（6）：618－622．

［8］ 张军保．基于对称alpha平稳分布的SAR图像复原算法研究［硕士论文］．北京：中国科学院电子学研究所，2005．Zhang J B．Synthetic Aperture Radar（SAR）image recovering with improving symmetric alpha－stable distribution method［Master′s thesis］（in Chinese）．Beijing：Institute of Electronics，Chinese Academy of Sciences，2005．

［9］ 胡睿，孙进平，王文光．基于α稳定分布的SAR图像目标检测算法．中国图像图形学报，2009，14（1）：25－29．Hu R，Sun J P，Wang W G．Target detection of SAR images using alpha stable distribution．Journal of Image and Graphics（in Chinese），2009，14（1）：25－29．

［10］ 郭文强．稳定分布噪声下的盲信号处理方法及应用研究［博士论文］．大连：大连理工大学，2007．Guo W Q．Study on method and applications of blind signal processing in stable noise［Ph．D．thesis］（in Chinese）．Dalian：Dalian University of Technology，2007．

［11］ Shuey R T．A simplification of the Zoeppritz equations．Geophysics，1985，50（4）：609－614．

［12］ Tsihrintzis G A，Nikias C L．Evaluation of fractional，lowerorder statistics－based detection algorithms on real radar seaclutter data．IEE Proceedings－Radar，Sonar and Navigation，1997，144（1）：29－38．

［13］ Shao M，Nikias C L．Signal processing with fractional lower order moments：stable processes and their applications．Proceeding of the IEEE，1993，81（7）：986－1010．

［14］ Gonzalez J G，Paredes J L，Arce G R．Zero－order statistics：a mathematical framework for the processing and characterization of very impulsive signals．IEEE Transactions on Signal Processing，2006，54（10）：3939－3851．

［15］ Joon L T．System Identification Using Novel Adaptive Filter Structures．Cambridge：University of Cambridge，1995．

［16］ Stuck B W．Minimum error dispersion linear filtering of scalar symmetric stable processes．IEEE Transactions on Automatic Control，1978，23（3）：507－509．

［17］ 邱天爽，杨志春，李小兵等．α稳定分布下的加权平均最小p－范数算法．电子与信息学报，2007，29（2）：410－413．Qiu T S，Yang Z C，Li X B，et al．A weighted average least p－norm algorithm under alpha stable noise conditions．Journal of Electronics ＆Information Technology（in Chinese），2007，29（2）：410－413．

［18］ 彭真明，李亚林，巫盛洪等．碳酸盐岩储层多角度弹性阻抗流体识别方法．地球物理学报，2008，51（3）：881－885．Peng Z M，Li Y L，Wu S H，et al．Discriminating gas and water using multi－angle extended elastic impedance inversion in carbonate reservoirs．Chinese J．Geophys．（in Chinese），2008，51（3）：881－885．

Seismic inversion method withα－stable distribution

YUE Bi－Bo1，PENG Zhen－Ming1，ZHANG Qi－Heng2

1 School of Opto－Electronic Information，University of Electronic Science and Technology of China，Chengdu610054，China
2 Institute of Optics and Electronics，Chinese Academy of Sciences，Chengdu610209，China

This paper briefly introduced the statistic characteristics ofα－stable distribution，analyzed the dynamic sample variance ofα－stable distribution and seismic signals comparatively，and proposed that seismic signals followα－stable distribution．Based on this，the cost function was built with the p－order statistics of seismic data estimated error．The least p－norm seismic inversion algorithm was proposed and applied to single－channel reflectivity inversion and real prestack elastic impedance inversion．Both of the applications obtained good results，which demonstrated that the seismic signals follow non－Gaussianα－stable distribution and the least pnorm seismic inversion algorithm was efficient and feasible．

α－stable distribution，non－Gaussian，Inversion，p－norm

P631收修定稿2011－03－01，2012－03－19收修定稿

国家自然科学基金（40874066，40839905）、国家科技重大专项（2008ZX05019－006）及中央高校基本科研业务费专项资金（ZYGX2011YB021）资助．

岳碧波，男，1984年生，博士研究生，主要从事信号与信息处理、叠前地震反演与储层预测研究工作．E－mail：yue＿bibo＠163．com

岳碧波，彭真明，张启衡．基于α稳定分布的地震反演方法．地球物理学报，2012，55（4）：1307－1317，

10．6038／j．issn．0001－5733．2012．04．026．

Yue B B，Peng Z M，Zhang Q H．Seismic inversion method withα－stable distribution．Chinese J．Geophys．（in Chinese），2012，55（4）：1307－1317，doi：10．6038／j．issn．0001－5733．2012．04．026．

10．6038／j．issn．0001－5733．2012．04．026

（本文编辑 何 燕）