甲烷晶体的晶格能和弹性性质:不同方法及泛函的评估
2012-12-12郑朝阳赵纪军
郑朝阳 赵纪军
(大连理工大学物理与光电工程学院,高科技研究院,辽宁大连116024)
1 Introduction
Dispersion interaction is originated from the interaction between the instantaneous dipoles of nearby atoms or molecules. It continues to be a challenge for theoretical chemistry and solid state physics.1Although the strength of dispersion force is much weaker than those of covalent,metallic,or ionic bonding,the van der Waals(vdW)interaction becomes dominant in the condensed phases of rare gases,molecular crystals,layered solids(like graphite),etc.Till now,the computational physicists and computational chemists have made significant efforts to an accurate description of the dispersion interaction.2-5Due to the lack of long-range correlation,the standard density functional theory(DFT)methods based on local density approximation(LDA)or generalized gradient approximation(GGA) were shown to be insufficient to describe vdW interaction.For instance,Johnson and DiLabio3examined six DFT functionals for predicting binding energies and structure for 28 vdW dimmers and found that no standard DFT method can provide a consistently accurate treatment of dispersion-bound complexes.Zhao and Truhlar5assessed forty DFT functionals for noncovalent interaction energies of biological importance.They showed that B3LYP and PBE0 functionals fail to describe the interactions in the dispersion-dominated complexes.
Recently,there have been some attempts of adding dispersive interaction into the standard density functional theory,for example,the DFT with dispersion energy correction(DFT-D) methods.In a pioneering work,Gianturco et al.6investigated the interaction between Ar and CO using standard DFT calculation combined with a damped dispersion energy.Wu and Yang7implemented the vdW energy correction into DFT calculations and studied the effect of the damping functions and the DFT functionals.Grimme and co-workers8-10systematically studied the empirical correction to account for vdW interactions within DFT functionals and they developed a series of DFT-D methods(DFT-D2 and DFT-D3),which have been widely used in the present research.They applied these methods to study hydrogen-bonded complexes,non-aromatic complexes,benzene complexes,complexes of larger aromatic molecules and DNA base pairs.For example,the mean absolute deviation of heat of formation for G97/2 set is only 3.8 kcal·mol-1(15.9 kJ· mol-1).9Ortmann et al.11developed a semiempirical method based on a few simple assumptions that corrects DFT-GGA by including dispersion forces.The semiempirical vdW-corrected GGA functional was applied to crystalline systems such as graphite,hexagonal boron nitride(h-BN)and rare-gas solid, molecular and dimerized systems to probe the universality and transferability of this correction.Recently,Tkatchenko and Scheffler12presented an accurate method to obtain molecular C6coefficients of potential form C6R-6(R represents the distance between two interacted atoms)from ground-state electron density and reference values for the free atom.They found that the C6coefficients depended strongly on the bonding environment of an atom.In general,DFT-D method shows asymptotically correct and can be easily combined with standard or other exchange-correction functionals.13
The dimer and solid of methane serve as ideal prototype systems to study the vdW interaction because the CH4molecule possesses close-shell electron configuration with totally eight valence electrons and carries no permanent dipole moment.In other words,the interaction between methane molecules is purely vdW force due to induced dipole-induced interaction. Previously,Tsuzuki et al.14-18carried out a series of studies on the nonbonding interactions of methane dimer using various theoretical methods,including the Hartree-Fock(HF)theory, the second-order and fourth-order Møller-Plesset perturbation theories(MP2 and MP4),the coupled-cluster theory with singles,doubles,and perturbative triples excitations(CCSD(T)), and the density functional theory.They found that MP4 (SDTQ)was close to CCSD(T)for electron correlation energies and dispersion interaction was not covered by DFT methods using BLYP,BPW91,and B3LYP functionals.16Li and Chao19calculated the intermolecular potentials of the methane dimer at the most stable D3dconformation with Møller-Plesset perturbation theory and density functional theory.
In addition to methane dimer,methane solid has been studied both experimentally and theoretically.Using X-ray diffraction(XRD)technology,Hazen et al.20measured the lattice parameters of crystalline methane under high pressures(up to 5.21 GPa)and determined the isothermal bulk modulus((4.9± 0.9)GPa)from the first-order Murnaghan equation of state.Bini and Pratesi21constructed a phase diagram for solid methane using high-pressure infrared spectra up to 30 GPa between 50 and 300 K.Thermodynamic properties of CH4and heavy methane(CD4)have been studied experimentally by Colwell and co-workers.22They accounted for the apparent zero-point entropies and the mechanism of thermal transitions of both solid CH4and CD4.Press23also studied the structure and phase transitions of solid CD4using XRD technology.Shimizu et al.24studied the pressure effect on rotation-translation via high-pressure elastic properties of liquid and solid methane using Brillouin spectroscopy.Nakahata et al.25performed the XRD measurements for solid methane up to 13 GPa and revealed that the high-pressure structure of solid methane is rhombohedral with a bulk modulus of 7.9 GPa
On the theoretical side,the cohesive energy and crystal structure of solid methane have been studied using different computational methods by Kimel et al.26and Kunz,27respectively. Kimel et al.calculated the possible structures of solid methane using the intermolecular potential consisting of repulsive and attractive interactions between nonbonded atoms.They obtained the best structure of symmetry D3dand other properties of solid methane with distortion.Kunz27simulated the cohesive properties,electronic structure,and optical properties of solid methane using local orbital approach and many body perturbation theory(MBPT)based on Hartree-Fock method and was able to predict the accurate lattice parameter and the binding energy.The phase transition28,29and electronic band structure30,31of solid methane have also been studied by several groups.
Despite of the above efforts,there were only few studies of the vdW interaction in molecular crystals using DFT-D functionals.32-34The performance of the popular DFT functionals and DFT-D functionals for the solid methane as a prototype vdW system is crucial to the further applications of these theoretical methods in the other molecular crystals.In this paper, we investigate the intermolecular interaction in terms of lattice energy,lattice constant,and bulk modulus of solid methane using different functionals.The comparison of our theoretical results with experiments provides very useful information for the validity of these DFT methods.
2 Computational methods
The crystalline structure of solid methane(Fig.1)is an fcc lattice with four CH4molecules per unit cell,with the central carbon atom of CH4sitting on each lattice point.DFT calculations were performed using planewave pseudopotential techniqueasimplemented in theCASTEP program.35The norm-conserving pseudopotentials36were adopted to describe the ion-electron interactions.The energy cutoff of planewave was set to 750 eV and the Brillouin zone was sampled by a 3× 3×3 k point mesh.Our test calculations show that further raising the cutoff energy or the number of k points leads to only minor changes on the computational results.
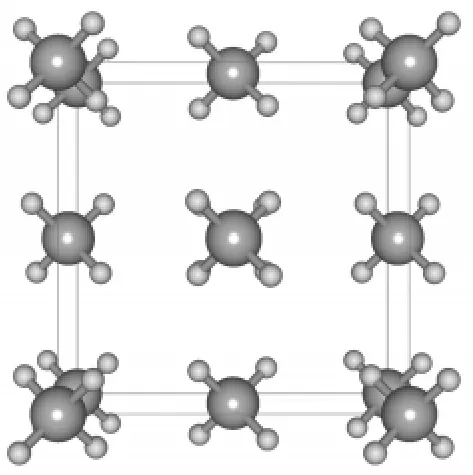
Fig.1 Atomic structure of solid methane(perspective view)of fcc lattice
Here we used a variety of density functionals for describing the exchange correction interaction.They can be categorized into four types:(i)CA-PZ37,38within local density approximation(LDA);(ii)standard(pure)PBE,39RPBE,40PW91,41and WC42functionals within generalized gradient approximation (GGA);(iii)hybrid sX-LDA,43B3LYP,44,45and PBE046functionals;(iv)DFT-D schemes including the DFT-Grimme by Grimme,8DFT-OBS by Ortmann,Bechstedt and Schmidt,11and DFT-TS by Tkatchenko and Scheffler.12
For a molecular crystal,the strength of intermolecular interaction can be characterized by the lattice energy47defined as:

where Elattis the lattice energy per molecule,Ecrysis the total energy per unit cell of the crystal,n is the number of molecules per unit cell,and Emolis the total energy of the gas phase molecule.
The bulk modulus(B)was calculated using the following third-order Birch-Murnaghan equation of state(EOS)48for thecurve:
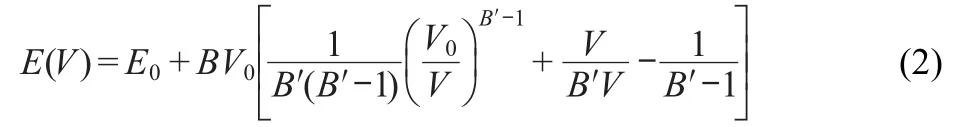
where the volume(V)is determined by V=a3for cubic systems, V0represents the volume at the energy minimum E0,Bʹis the derivative of the bulk modulus at the zero pressure,which was set as 4.0.
3 Results and discussion
Table 1 summarizes the theoretical lattice energy(Elatt),lattice parameter(a),and bulk modulus(B)of solid methane obtained from different DFT methods,along with experimental data.27Fig.2 shows several representative curves of lattice ener-gy versus lattice parameter for selected DFT methods.Fig.3 compares the lattice energies and bulk modulus calculated by different functionals with experimental value.
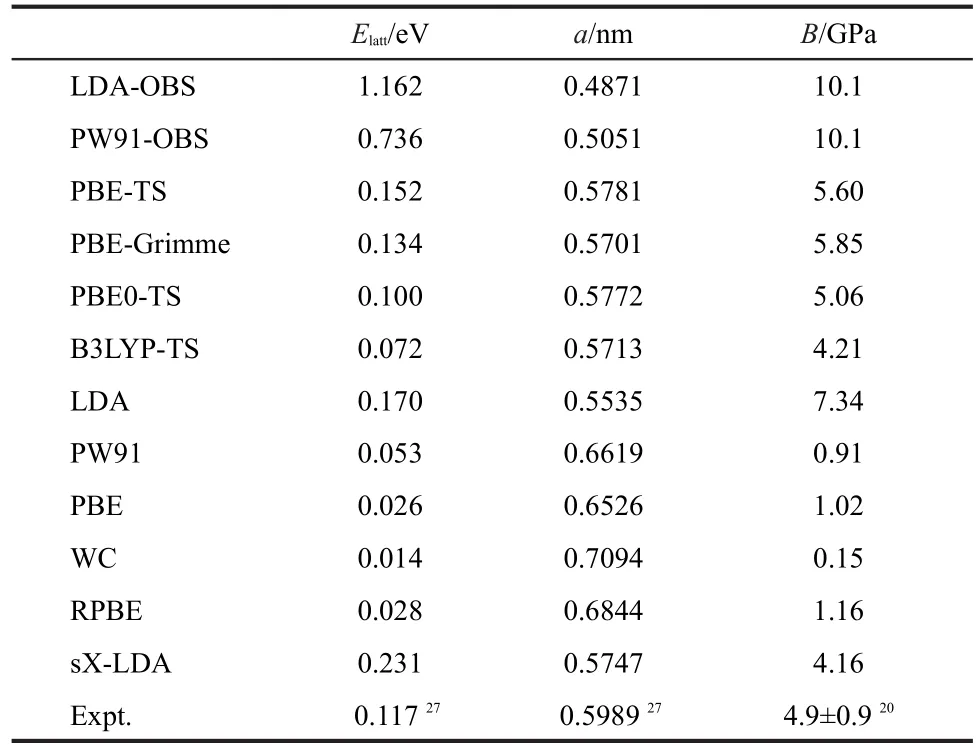
Table 1 Lattice parameter(a),lattice energy(Elatt),and bulk modulus(B)of solid methane calculated from different DFT functionals and experiments
Clearly,most of standard GGA functionals except PW91 functional significantly underestimate intermolecular interaction.For example,the lattice energy obtained from PBE functional is 0.026 eV,which is only about 22%of the experiment value of 0.117 eV.27The smallest binding strength(Elatt=0.014 eV)is predicted by the WC functional.Among those pure GGAfunctionals considered,PW91 yields the largest lattice energy of 0.053 eV,which is about half of the experimental strength.Previously,Tsuzuki and Lüthi49also found that PW91 can partially give the description of the dispersion interactions. In contrast,LDA overestimates the intermolecular lattice energy of solid methane by 45%.These results are in agreement with previous studies by Slough and Perger,34who found that the B3LYP-D potential showed promise for prediction of structure and elastic properties in molecular crystals.
As for the hybrid functionals,some of them(such as PBE0, B3LYP,and HF-LDA)show no maximum lattice energy on the binding curve,indicating that the solid methane described by these methods is not even locally stable.On the contrary, sX-LDA yields large lattice energy of 0.231 eV,severely overestimated the CH4-CH4interaction by about twice of magnitude with regard to experiment.
Since all above functionals can not describe the binding interaction in the molecular solid well,they are not able to give reasonable lattice parameters of solid methane.Accordingly, most pure and hybrid GGA functionals overestimate the lattice parameter,while LDA and sX-LDA underestimate.For example,PBE functional predicts a lattice parameter of 0.6526 nm, while LDA gives 0.5535 nm,compared with the experiment value of 0.5989 nm.27
The most exciting result is that some DFT-D methods(such as PBE-TS,PBE-Grimme,PBE0-TS,and B3LYP-TS)give better description of intermolecular interaction than those stan-dard DFT methods.Among them,the lattice energies predicted by the PBE0-TS(0.1 eV)and PBE-Grimme(0.134 eV)are closest to the experiment value(0.117 eV).27However,as shown in Table 1 and Fig.3,some DFT-D functionals like PW91-OBS and LDA-OBS overcorrects the binding properties severely and yields too large lattice energies(0.736 or 1.162 eV).Meanwhile,all DFT-D methods underestimate lattice parameter of solid methane(see Table 1).In particular,the DFT-D methods which overestimate the lattice energy also underestimate the lattice parameter severely.For instance,the lattice parameter from PW91-OBS functional is 0.5051 nm, which is 15.7%smaller than experimental value of 0.5989 nm.27Among the methods considered,the lattice constants from sX-LDA,PBE-TS,PBE0-TS are relatively closer to experiment,with deviation of about 4%.
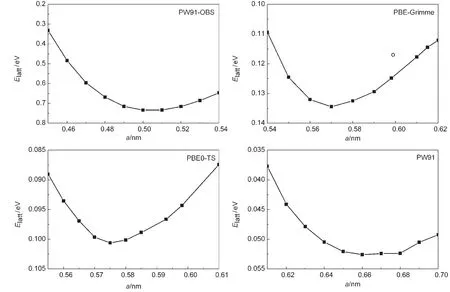
Fig.2 Lattice energy versus cell parameter of solid methane for selected DFT methodsThe lines are connecting these data points simply,and the open circle dot is the experimental values.27

Fig.3 Lattice energies(a)and bulk modulus(b)of solid methane calculated using different DFT functionalsThe experiment value of 0.117 eV27for lattice energy and 4.9 GPa20for bulk modulus were marked by dashed lines.
Since the intermolecular interaction is rather weak,there is no noticeable difference in the geometry parameters in the gas-phase molecule and solid methane described with the same functional.For example,the C―H bond length is 0.1091 nm for both individual methane molecule and solid methane from calculation using PBE functional,which is in good agreement with the experimentally spectroscopic data of(0.1086± 0.0001)nm for CH4molecule.40
To ensure a good description of intermolecular vdW force,it is crucial to examine the performance of the DFT methods for a molecular solid under high-pressure compression,which corresponds to shorter intermolecular distance.For each DFT method,we computed the Elatt-a curve and fitted the Birch-Murnaghan equation of state to obtain the bulk modulus B.The calculated bulk moduli are listed in Table 1.One can see that all pure GGA functionals underestimate the bulk modulus of solid methane because they underestimate the bonding property of weak interactions system.For example,the bulk modulus of solid methane using PBE functional is only 1.02 GPa,compared to the experiment value of(4.9±0.9)GPa.20Naturally, those functionals that overestimate the binding properties of solid methane,such as LDA,PW91-OBS,and LDA-OBS,also overestimate the bulk modulus.Again,the PBE0-TS and PBEGrimme methods yield reasonable values of 5.06 and 5.85 GPa,respectively,which agree satisfactorily with experiment value.20In addition,the bulk modulus(5.60 GPa)given by PBE-TS calculation is also acceptable.
4 Conclusions
In the present study,we examined the description of vdW interactions in a prototype molecular solid of methane by a variety of DFT methods,including LDA,standard GGA,hybrid GGA,and DFT-D.The lattice constant,lattice energy,and bulk modulus of solid methane were calculated using different DFT methods and compared with experimental data.Without dispersion correction,LDA as well as pure or hybrid GGA fail to reproduce the intermolecular vdW interaction of solid methane. Our calculations show that the PBE0-TS and PBE-Grimme functionals are able to describe the vdW interaction of solid methane well,and the performance of PBE-TS is also acceptable.Considering the high computational cost of the hybrid DFT functional like PBE0,dispersion-corrected PBE functionals,such as PBE-Grimme and PBE-TS are recommended as the reasonable choice for studying the vdW solid.
(1) Dobson,J.F.;McLennan,K.;Rubio,A.;Wang,J.;Gould,T.; Le,H.M.;Dinte,B.P.Aust.J.Chem.2001,54(8),513.doi: 10.1071/CH01052
(2) Johnson,B.;Gill,P.;Pople,J.J.Chem.Phys.1993,98(7), 5612.doi:10.1063/1.464906
(3) Johnson,E.R.;DiLabio,G.A.Chem.Phys.Lett.2006,419 (4-6),333.doi:10.1016/j.cplett.2005.11.099
(4) Zhang,Y.;Pan,W.;Yang,W.J.Chem.Phys.1997,107(19), 7921.doi:10.1063/1.475105
(5) Zhao,Y.;Truhlar,D.G.J.Chem.Theory Comput.2006,3(1), 289.
(6) Gianturco,F.A.;Paesani,F.;Laranjeira,M.F.;Vassilenko,V.; Cunha,M.A.J.Chem.Phys.1999,110(16),7832.doi:10.1063/ 1.478690
(7)Wu,Q.;Yang,W.J.Chem.Phys.2002,116(2),515.doi: 10.1063/1.1424928
(8) Grimme,S.J.Comput.Chem.2004,25(12),1463.doi:10.1002/ jcc.20078
(9) Grimme,S.J.Comput.Chem.2006,27(15),1787.doi:10.1002/ jcc.20495
(10) Grimme,S.;Antony,J.;Ehrlich,S.;Krieg,H.J.Chem.Phys. 2010,132(15),154104.doi:10.1063/1.3382344
(11) Ortmann,F.;Bechstedt,F.;Schmidt,W.G.Phys.Rev.B 2006, 73(20),205101.doi:10.1103/PhysRevB.73.205101
(12) Tkatchenko,A.;Scheffler,M.Phys.Rev.Lett.2009,102(7), 073005.doi:10.1103/PhysRevLett.102.073005
(13) Grimme,S.Wires Comput.Mol.Sci.2011,1(2),211.doi: 10.1002/wcms.30
(14) Tsuzuki,S.;Tanabe,K.J.Phys.Chem.1991,95(6),2272.doi: 10.1021/j100159a032
(15)Tsuzuki,S.;Uchimaru,T.;Mikami,M.;Tanabe,K.J.Phys. Chem.A 1998,102(12),2091.doi:10.1021/jp973467d
(16) Tsuzuki,S.;Uchimaru,T.;Tanabe,K.Chem.Phys.Lett.1998, 287(1-2),202.doi:10.1016/S0009-2614(98)00159-6
(17)Tsuzuki,S.;Uchimaru,T.;Tanabe,K.Chem.Phys.Lett.1998, 287(3-4),327.doi:10.1016/S0009-2614(98)00193-6
(18) Tsuzuki,S.;Uchimaru,T.;Tanabe,K.;Kuwajima,S.J.Phys. Chem.1994,98(7),1830.
(19) Li,A.H.T.;Chao,S.D.J.Chem.Phys.2006,125(9),094312. doi:10.1063/1.2345198
(20) Hazen,R.;Mao,H.;Finger,L.;Bell,P.Appl.Phys,Lett.1980, 37(3),288.doi:10.1063/1.91909
(21) Bini,R.;Pratesi,G.Phys.Rev.B 1997,55(22),14800.doi: 10.1103/PhysRevB.55.14800
(22) Colwell,J.;Gill,E.;Morrison,J.J.Chem.Phys.1964,40(7), 2041.doi:10.1063/1.1725446
(23) Press,W.J.Chem.Phys.1972,56(6),2597.doi:10.1063/ 1.1677586
(24) Shimizu,H.;Nakashima,N.;Sasaki,S.Phys.Rev.B 1996,53 (1),111.doi:10.1103/PhysRevB.53.111
(25)Nakahata,I.;Matsui,N.;Akahama,Y.;Kawamura,H.Chem. Phys.Lett.1999,302(3-4),359.doi:10.1016/S0009-2614(99) 00092-5
(26) Kimel,S.;Ron,A.;Hornig,D.J.Chem.Phys.1964,40(11), 3351.doi:10.1063/1.1725006
(27) Kunz,A.B.J.Phys.Condens.Mat.1994,6(17),L233.
(28) Spanu,L.;Donadio,D.;Hohl,D.;Galli,G.J.Chem.Phys. 2009,130(16),164520.doi:10.1063/1.3120487
(29)Yamamoto,T.;Kataoka,Y.Phys,Rev.Lett.1968,20(1),1.doi: 10.1103/PhysRevLett.20.1
(30) Kunz,A.B.Phys.Rev.B 1974,9(12),5330.doi:10.1103/ PhysRevB.9.5330
(31) Piela.L.;Pietronero,L.;Resta,R.Phys.Rev.B 1973,7(12), 5321.doi:10.1103/PhysRevB.7.5321
(32) Bucko,T.S.;Hafner,J.R.;Lebègue,S.B.;Ángyán,J.N.G. J.Phys.Chem.A 2010,114(43),11814.doi:10.1021/ jp106469x
(33) Shimojo,F.;Wu,Z.;Nakano,A.;Kalia,R.K.;Vashishta,P. J.Chem.Phys.2010,132(9),094106.doi:10.1063/1.3336452
(34) Slough,W.;Perger,W.F.Chem.Phys.Lett.2010,498(1-3), 97.doi:10.1016/j.cplett.2010.08.049
(35) Clark,S.J.;Segall,M.D.;Pickard,C.J.;Hasnip,P.J.;Probert, M.I.J.;Refson,K.;Payne,M.C.Zeitschrift für Kristallographie 2005,220(5-6),567.doi:10.1524/ zkri.220.5.567.65075
(36) Hamann,D.R.;Schlüter,M.;Chiang,C.Phys,Rev.Lett.1979, 43(20),1494.doi:10.1103/PhysRevLett.43.1494
(37) Ceperley,D.M.;Alder,B.J.Phys.Rev.Lett.1980,45(7),566. doi:10.1103/PhysRevLett.45.566
(38) Perdew,J.P.;Zunger,A.Phys.Rev.B 1981,23(10),5048.doi: 10.1103/PhysRevB.23.5048
(39) Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996,77 (18),3865.doi:10.1103/PhysRevLett.77.3865
(40) Hammer,B.;Hansen,L.B.;Nørskov,J.K.Phys.Rev.B 1999, 59(11),7413.doi:10.1103/PhysRevB.59.7413
(41) Perdew,J.P.;Wang,Y.Phys.Rev.B 1992,45,13244. doi:10.1103/PhysRevB.45.13244
(42) Wu,Z.;Cohen,R.E.Phys.Rev.B 2006,73(23),235116.doi: 10.1103/PhysRevB.73.235116
(43) Seidl,A.;Görling,A.;Vogl,P.;Majewski,J.A.;Levy,M.Phys. Rev.B 1996,53(7),3764.doi:10.1103/PhysRevB.53.3764
(44) Becke,A.D.J.Chem.Phys.1993,98(7),5648.doi:10.1063/ 1.464913
(45) Lee,C.;Yang,W.;Parr,R.G.Phys.Rev.B 1988,37(2),785. doi:10.1103/PhysRevB.37.785
(46)Adamo,C.;Barone,V.J.Chem.Phys.1999,110(13),6158. doi:10.1063/1.478522
(47)Perger,W.F.;Pandey,R.;Blanco,M.A.;Zhao,J.Chem.Phys. Lett.2004,388(1-3),175.doi:10.1016/j.cplett.2004.02.100
(48) Birch,F.Phys.Rev.1947,71(11),809.
(49) Tsuzuki,S.;Lüthi,H.P.J.Chem.Phys.2001,114(9),3949. doi:10.1063/1.1344891
(50) Gray,D.L.;Robiette,A.G.Mol.Phys.1979,37(6),1901.doi: 10.1080/00268977900101401