考虑刚性弹弹头形状的混凝土(岩石)靶体侵彻深度半理论分析*
2012-12-12龚自明
吴 昊,方 秦,龚自明
(1.中国工程物理研究院总体工程研究所,四川 绵阳621900;2.解放军理工大学国防工程学院,江苏 南京210007)
动能弹对混凝土和岩石靶体的冲击破坏效应是防护工程和武器研发领域的研究重点之一。表征靶体破坏效应的最主要参数就是弹体的侵彻深度(弹体侵入靶体的垂直距离)。对于中低速冲击而言(小于900m/s),侵彻深度研究一般基于两点假设:(1)弹体视为刚体,不考虑弹体的变形和质量侵蚀;(2)将弹体对靶体的冲击侵彻过程视为靶体的局部响应,不考虑弹体冲击作用下靶体的整体运动。
预测弹体侵彻深度的计算公式,主要分经验公式和半经验半理论公式两类。经验公式基于对野外原型或缩比模型弹体冲击实验数据拟合得到,常用的针对混凝土靶体的有BRL公式、ACE公式和修正的NDRC公式等[1],针对岩石靶体的有Young公式、Bernard公式和修正的别列赞(BLZ)公式等[2]。半经验半理论侵彻深度计算的研究中,M.J.Forrestal和D.J.Frew等基于空腔膨胀理论估算弹体侵彻靶体的阻力,进而提出了弹体侵彻深度计算公式Ⅰ[3-4]和Ⅱ[5-7]。X.W.Chen等[8]和 Q.M.Li等[9-10]基于两阶段侵彻模型,采用滑移线场理论得到了靶体开坑区的深度,引入了量纲一弹头形状函数和冲击因子,基于对弹头轮廓曲线方程的定义,进一步将Forrestal公式量纲一化,并能够适用于任意弹头形状。L.X.Qian等[11]引入靶体阻力系数和靶体强度参数,针对截卵形弹头的侵彻问题进行了半理论研究,但上述参数需要大量实验确定,并且只适用于截断部分长度小于弹身长度1/3的情况。A.T.Jan等[12]通过改进弹体阻力计算公式,将Forrestal侵彻模型推广到平头弹的情况,并且不用再引入经验参数。H.M.Wen[13]认为弹体侵彻过程中所受到的靶体阻力由靶体材料弹塑性变形产生的准静态压力和弹体速度效应引起的动压力两部分组成,引入了与靶体材料压力相关的剪切强度,提出了岩石靶体的弹体侵彻深度计算公式。王明洋等[14]利用波阵面上的动量守恒关系和弹体表面的连续运动规律,得到了岩体对弹体的侵彻阻抗,进而得到了弹体侵彻岩石靶体的侵彻深度计算公式及其参数的确定方法。沈俊等[15]通过量纲分析,对大量岩石靶体的侵彻实验数据进行拟合,建立了岩石靶体侵彻深度计算公式。
已有的研究大多针对卵形弹和混凝土靶体,对异型弹冲击混凝土和岩石靶体的侵彻问题研究较少,对侵彻过程中弹靶间摩擦阻力影响的研究还不深入。本文中,认为岩石靶体侵彻深度的工程计算可以采用混凝土靶体的类似分析方法,基于混凝土材料的动力球型空腔膨胀理论和“冲击成坑+钻孔区”两阶段侵彻模型,以截卵形弹头弹体为例,利用曲面积分的方法,得到能够综合考虑弹靶摩擦阻力、成坑区深度和弹头形状等参数影响的混凝土和岩石靶体垂直侵彻深度的计算公式。
1 侵彻深度计算
以截卵形弹头弹体为例,如图1所示。其中弹身直径为d,截断部分直径为d1,卵形弹头总长度为l,截断部分长度为l1,弹头的曲率半径为s,x为弹体位移,箭头所指方向为弹体运动方向,θ为弹体运动方向与弹头圆弧法线方向的夹角,v0为弹体的初始冲击速度。

图1 截卵形弹头示意图Fig.1 Sketch map of truncated-ogive nose projectile
许多混凝土和岩石靶体侵彻实验表明,靶体的破坏形态为一个近似倒锥形的冲击坑和一个直径近似等于弹体直径的钻孔区组成。本文中采用“冲击成坑+钻孔区”两阶段侵彻模型,如图2所示,其中冲击坑深度为Hc,弹体侵彻深度为Hp。文献[3-4]表明,靶体开坑区深度与弹体直径成正比,可表示为Hc=kd,其中k为开坑区深度系数。对于卵形弹,M.J.Forrestal等[16]基于实验,得出k=2,Q.M.Li等[9]基于滑移线理论,得出k=0.707+l/d。对于截卵形弹头,则有k=0.707+(l-l1)/d。

图2 两阶段侵彻模型Fig.2 Two-stage penetration model
当Hp≤Hc时,弹体侵彻只形成开坑区,基于已有实验对弹体过载特性的测量,开坑区弹体所受阻力Fcr与弹体侵彻深度x成线性关系。对于典型的截卵形弹头,可表示为[11]

式中:c为阻力系数。由式(1)得出弹体在开坑区的运动方程为

式中:M 为弹体质量。初始条件为:x(0)=0,x′(0)=v0,求解上述微分方程可以得到侵彻深度

积分式(2)得到开坑区弹体的位移、速度和加速度表达式
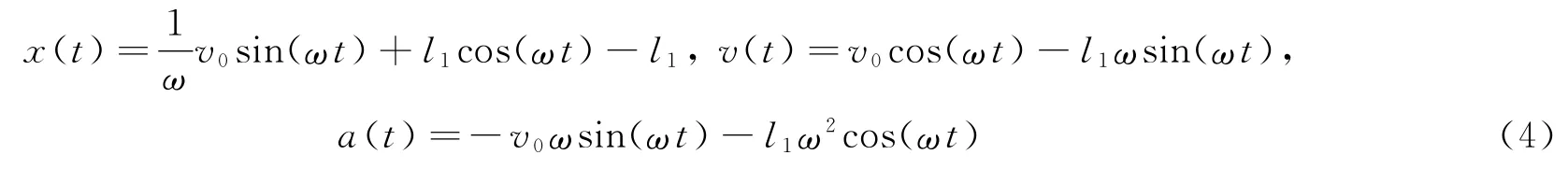
式中:ω2=c/M,0≤x≤kd。
当Hp>Hc时,弹体侵彻过程形成开坑区和坑下的钻孔区,其中开坑区深度满足Hc=kd。在钻孔区,由动力球型空腔膨胀理论,得到弹体侵彻混凝土靶体过程中弹体头部空腔法向膨胀压缩应力σn与法向膨胀速度vr的关系式[16],本文中认为对于岩石靶体同样满足

式中:S为靶体的强度参数,fc为靶体的抗压强度,ρ为靶体密度。S基于大量不同强度靶体侵彻实验数据回归得到,文献[3-4]中提出S=82.6(10-6fc)-0.544,文献[9]中提出S=72(10-6fc)-0.5,而两式在fc≥15MPa时基本相等,因此本文中取S=82.6(10-6fc)-0.544。
侵彻过程(见图1)中,弹体头部空腔的法向膨胀速度vr与弹体即时侵彻速度v满足vr=vcosθ,弹体所受靶体的切向应力στ与法向应力σn满足στ=μmσn,其中μm为弹体和靶体间的滑动摩擦系数,一般取值范围为0~0.2[8,17-18]。
弹头截断部分和卵形部分在侵彻过程中受到的沿弹体运动方向的阻力分别为

式中:Σ 为弹头卵形部分侧面积。对于一般弹体构造,有θ0=arccos((l-l1)/s)和θ1=π/2。由式(6)得到钻孔区弹体所受到的阻力为

式中:G1和G2为表征弹头形状和弹靶摩擦效应的量纲一系数。定义弹头形状量纲一参数Φ=s/d,ζ1=l/d,ζ2=l1/d,ζ3=d1/d,由式(6)~(7),对于(截)卵形(包括半球形、平头形)弹有

对于(截)锥(包括平头形)形弹有
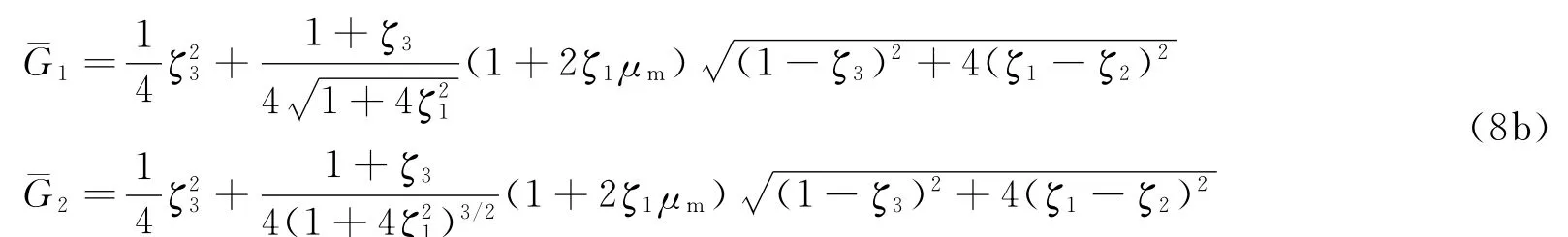
对于卵形弹和锥形弹,式(8)中取ζ2=ζ3=0;对于截卵(锥)形弹,式(8)中取ζ3=d1/d;对于半球形弹,式(8a)中取ζ2=ζ3=0,ζ1=Φ=0.5;对于平头弹,有ζ1=ζ2,ζ3=1,式(8a)和(8b)形式相同。
设冲击成坑区结束时刻为t1,弹体的速度为v1,由式(4)和(7)得出开坑区结束时刻(t=t1,v=v1,x=kd)两阶段弹体位移、速度和力的平衡条件为

由上式可求得
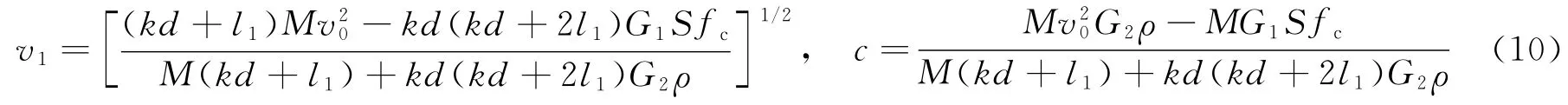
引入质量比λ=M/(ρd3),冲击因子I=Mv2/(d3fc),结合式(3)和(10)得到,当 Hp/d≤k时

由式(7)得出钻孔区弹体的运动方程,并积分得到,当Hp/d>k时
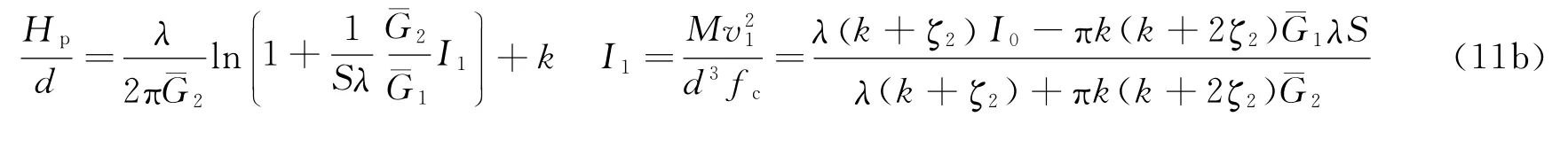
如果不考虑开坑区,即k=0,则由上式得到

对于中低速碰撞(v0<900m/s),当ζ3≠1(非平头弹)时,有I0G2/(G1Sλ)≪1,可将式(12)简化为

还有,当μm=0且ζ3≠1时,有I0G2/(G1Sλ)≪1并且G1≈0.25,则式(13)可进一步简化为

比较式(11)~(14)和已有应用较广的几个半理论公式可以得出:
(1)ForrestalⅠ公式[3-4]、Chen和 Li公式[8-10]和 Wen公式[13]中与本文公式中均考虑了开坑区深度,ForrestalⅠ公式、Chen和Li公式和 Wen公式中分别有k=2、k=0.707+(ζ1-ζ2)和k=ζ1。
(2)ForrestalⅡ公式[5-7]和 Wen公式[13]虽然精度较高,但公式中反映靶体强度的参数R 和Y 必须通过实际的实验侵彻深度反推得到,因此缺乏对侵彻深度的预测能力,本文中不作讨论。
(3)ForrestalⅠ公式[3-4]中仅考虑了卵形弹,并且没有考虑弹靶之间的摩擦力。当取ζ2=ζ3=0、k=2和μm=0时,式(11)退化为ForrestalⅠ公式。Chen和Li公式[8-10]可以考虑多种弹头形状,当μm=0且k=0.707+(ζ1-ζ2)时,式(11)分别取ζ2=ζ3=0、ζ2=ζ3=0和Φ=ζ1、ζ1=ζ2=0和ζ3=1时,和Chen和Li公式卵形弹、锥形弹、平头弹计算公式形式相同。
(4)从式(13)~(14)可以看出,非平头弹体的量纲一侵彻深度与冲击因子近似成系数为1/(2πSG1)的线性关系。当不考虑弹靶摩擦阻力时,上述线性系数简化为2/(πS)。对于平头弹(ζ3=1),IG2/(G1Sλ)≪1不满足,式(13)~(14)不成立,这点在已有研究中没有讨论过。
图3分别给出了基于表1中实验3,得到的量纲一侵彻深度随ζ3和Φ的变化曲线,为方便计算中取μm=0和k=0。由图可见,侵彻深度随Φ的增大而增大,随ζ3的增大而减小。因此采用卵(锥)形弹头并增加Φ,是提高弹体侵彻能力的有效途径。

图3 ζ3和Φ对侵彻深度的影响曲线Fig.3 Penetration depth curves for differentζ3andΦ
2 与实验结果比较
表1为8组混凝土和岩石靶体侵彻实验参数。用式(11)及已有10个(半)经验公式的弹体侵彻深度与相应实验结果进行比较,图4~5给出了表1中对应的混凝土和岩石靶体的侵彻深度。
由图4可见,对于混凝土靶体而言:
(1)弹体的量纲一侵彻深度随弹靶摩擦系数μm的增大而显著减小,并且μm对侵彻深度的影响随弹体冲击速度的增大而显著增大。当μm=0时,计算结果与实验数据吻合最好,因此对于非平头弹,可以采用简化式(14)进行计算。

表1 侵彻实验的相关参数Table 1 Parameters in projectile penetration experiments
(2)对于不同弹头形状弹体而言,量纲一侵彻深度随着开坑区深度系数k的增大而增加,并且随着弹头截断部分的不断增大,k对侵彻深度的影响也越来越大。通过对比得出,当ζ3≠1时,建议当钻孔区深度大于开坑区深度的2倍时,即初始冲击因子最小值满足I0,min≥2πSG1k2/(k+ζ2)时,可不考虑开坑区深度,采用式(12)计算,如实验1~3;否则,采用式(11)计算,取k=0.707+(ζ1-ζ2);当ζ3=1时,取k=0.707,如实验4。
(3)图4(c)~(d)中,取μm=0和k=0.707+(l-l1)/d 时,式(11)的计算结果和Chen和Li公式计算结果的误差,在于靶体强度参数S不同。
(4)式(11)的计算结果优于常用的三个经验公式计算结果。经验公式中,BRL公式和ACE公式分别用于卵形弹和异形弹计算时的精度最高。
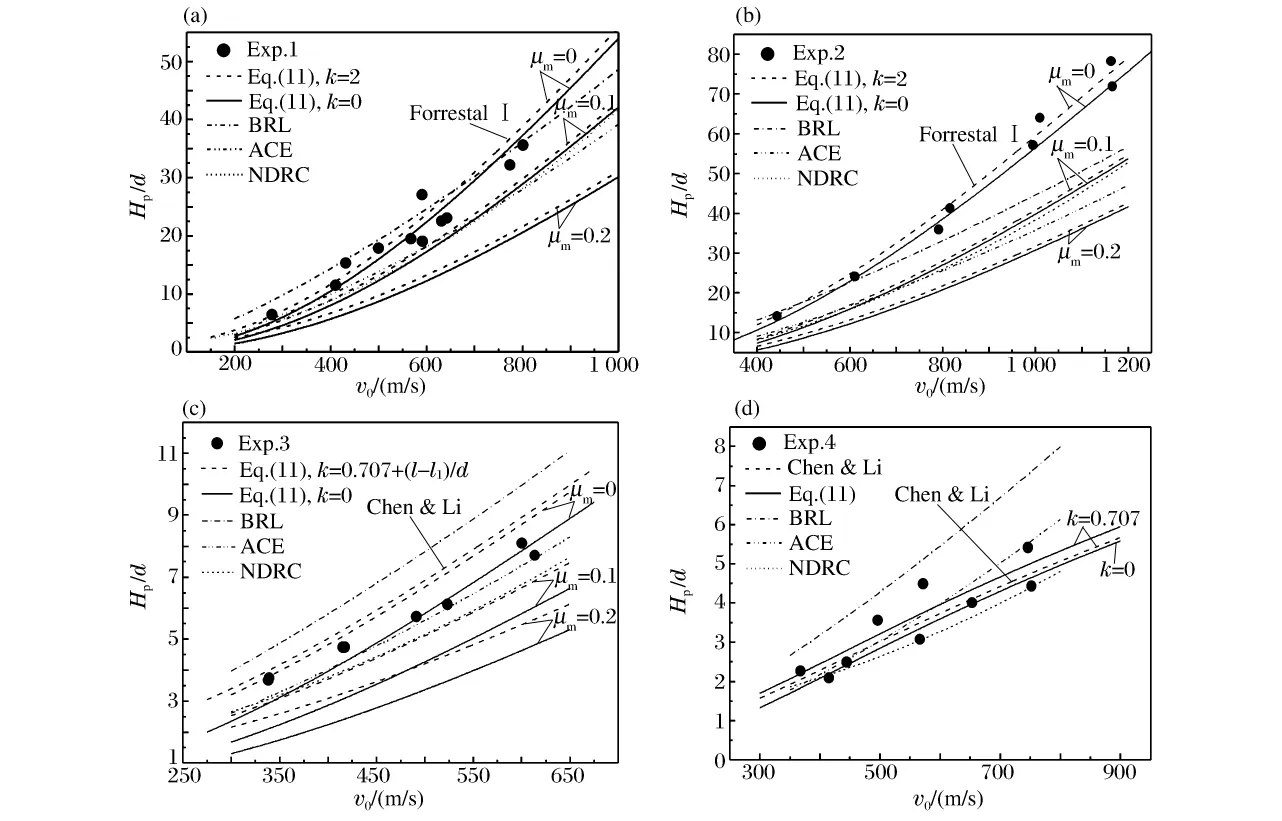
图4 混凝土靶体侵彻深度Fig.4 Penetration depth curves for concrete target
对于卵形弹,实验5~6和8满足I0≥2πSG1k2/(k+ζ2),计算中采用式(12)。实验7满足I0<2πSG1k2/(k+ζ2),计算中采用式(11)。由图5可见,对于岩石靶体而言:
(1)普通和高强岩石靶体的侵彻问题同样可以用混凝土靶体侵彻分析方法进行研究。
(2)和混凝土靶体相同,弹体侵彻岩石靶体的量纲一侵彻深度随弹靶摩擦系数μm的增大而显著减小,并且μm对侵彻深度的影响随弹体冲击速度的增大而显著增大。对于岩石靶体时,需考虑弹靶间的摩擦阻力。对于普通和高强岩石靶体,当μm分别取0.05和0.1时,计算结果与实验数据吻合最好。
(3)岩石靶体的侵彻深度计算中,成坑区系数的取值可参照混凝土靶体。
(4)式(11)的计算结果优于(半)经验公式计算结果。经验公式中,Bernard公式预测精度最高。
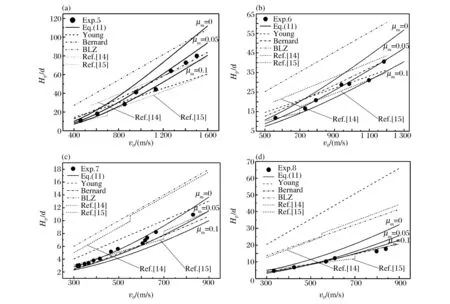
图5 岩石靶体侵彻深度Fig.5 Penetration depth curves for rock target
3 结 论
基于动力球型空腔膨胀理论和“冲击成坑+钻孔区”两阶段侵彻模型,以截卵形弹头弹体为例,利用曲面积分方法,得到了能够综合考虑弹靶摩擦阻力、成坑区深度和弹头形状等参数影响的混凝土和岩石靶体侵彻深度的计算公式。
(1)本文公式在相关参数取特殊值时退化为经典的ForrestalⅠ公式[3-4]。与8组不同弹头形状弹体侵彻混凝土和岩石靶体的实验数据、10个(半)经验公式的计算结果对比,验证了本文公式的适用性。
(2)对于混凝土靶体,建议弹靶摩擦系数取0,非平头弹体中低速侵彻混凝土靶体的量纲一侵彻深度与冲击因子近似成系数为2/(πS)的线性关系;对于普通和高强岩石靶体,建议弹靶摩擦系数分别取0.05和0.1,非平头弹体中低速侵彻岩石靶体的量纲一侵彻深度与冲击因子近似成系数为1/(2πSG1)的线性关系。
(3)对于混凝土和岩石靶体侵彻深度的计算,当ζ3≠1且I0,min≥2πSG1k2/(k+ζ2)时,可不考虑开坑区深度,采用式(12)计算;否则,采用式(11)计算,取k=0.707+(ζ1-ζ2);当ζ3=1时,取k=0.707。
(4)经验公式中,BRL公式、ACE公式和Bernard公式分别用于混凝土和岩石靶体侵彻深度计算时的预测精度最高。
(5)受已有实验限制,仅针对普通混凝土靶体的(截)卵形和平头弹以及岩石靶体的卵形弹侵彻深度问题进行了探讨。式(11)对于如高强混凝土靶体的侵彻问题以及平头弹侵彻岩石靶体等工况中侵彻深度的预测能力,有待进一步的实验验证。另外,对于弹靶摩擦系数的取值范围0~0.2,只是一种工程方法,对于弹靶摩擦机理以及与弹体即时速度相关的摩擦系数的取值也是进一步工作的重点。
[1]Li Q M,Reid S R,Wen H M,et al.Local impact effects of hard missiles on concrete targets[J].International Journal of Impact Engineering,2005,32:224-284.
[2]周健南,王斌,金丰年,等.侵彻岩石深度计算公式对比分析[J].弹箭与制导学报,2007,27(5):119-121.ZHOU Jian-nan,WANG Bin,JING Feng-nian,et al.Analysis on depth calculation of projectiles penetration into rocks[J].Journal of Projectile,Rockets,Missiles and Guidance,2007,27(5):119-121.
[3]Forrestal M J,Frew D J,Hanchak S J.Penetration of grout and concrete targets with ogive-nose steel projectiles[J].International Journal of Impact Engineering,1996,18(5):465-476.
[4]Frew D J,Hanchak S J,Green M L.Penetration of concrete targets with ogive-nose steel rods[J].International Journal of Impact Engineering,1998,21(6):489-497.
[5]Frew D J,Forrestal M J,Hanchak S J.Penetration into limestone targets with ogive-nose steel projectile[J].Journal of Applied Mechanics,2000,67:841-845.
[6]Forrestal M J,Frew D J,Hickerson J P.Penetration of concrete targets with deceleration-time measurements[J].International Journal of Impact Engineering,2003,28:479-497.
[7]Frew D J,Forrestal M J,Cargile J D.The effect of concrete target diameter on projectile deceleration and penetration depth[J].International Journal of Impact Engineering,2006,32:1584-1594.
[8]Chen X W,Li Q M.Deep penetration of a non-deformable projectile with different geometrical characteristics[J].International Journal of Impact Engineering,2002,27:619-637.
[9]Li Q M,Chen X W.Dimensionless formulae for penetration depth of concrete targets impacted by rigid projectiles[J].International Journal of Impact Engineering,2003,28:93-116.
[10]Li Q M,Weng H J,Chen X W.A modified model for the penetration into moderately thick plates by a rigid,sharp-nosed projectile[J].International Journal of Impact Engineering,2004,30:193-204.
[11]Qian L X,Yang Y B,Liu T.A semi-analytical model for truncated-ogive-nose projectiles penetration into semi-infinite concrete targets[J].International Journal of Impact Engineering,2000,24:947-955.
[12]Jan A T,Henrik S.Penetration into concrete by truncated projectiles[J].International Journal of Impact Engineering,2004,30:447-464.
[13]Wen H M.Predicting the penetration and perforation of targets struck by projectiles at normal incidence[J].Mechanics of Structures and Machines,2002,30(4):543-577.
[14]王明洋,谭可可,吴华杰,等.钻地弹侵彻岩石深度计算新原理与方法[J].岩石力学与工程学报,2009,28(9):1863-1868.WANG Ming-yang,TAN Ke-ke,WU Hua-jie,et al.New method of calculation of projectile penetration into rock[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(9):1863-1868.
[15]沈俊,刘瑞朝,杨建超,等.弹体侵彻岩体效应试验与理论研究[J].岩石力学与工程学报,2008,27(5):946-952.SHEN Jun,LIU Rui-chao,YANG Jian-chao,et al.Experimental and theoretical studies of projectile penetrating rocks[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(5):946-952.
[16]Forrestal M J,Altman B S,Cargile J D.An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J].International Journal of Impact Engineering,1994,15(4):395-405.
[17]Forrestal M J,Brar N S,Luk V K.Penetration of strain-hardening targets with rigid spherical-nose rodes[J].Journal of Applied Mechanics,1991,58(1):7-10.
[18]Mastilovic S,Krajcinovic D.Penetration of rigid projectiles through quasi-brittle materials[J].Journal of Applied Mechanics,1999,66:585-592.
[19]Forrestal M J,Cargile J D,Tzou R D Y.Penetration of concrete targets[R].SAND-92-2513C,1993.
[20]左魁,张继春,曾宪明,等.BLU-109B模型弹在岩石介质中成坑效应实验研究[J].岩石力学与工程学报,2007,26(增1):2767-2771.ZUO Kui,ZHANG Ji-chun,ZENG Xian-ming,et al.Experimental study on formation on craters in rock with BLU-109Bearth penetrating model projectiles[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(suppl 1):2767-2771.
[21]张德志,张向荣,林俊德,等.高强钢弹对花岗岩正侵彻的实验研究[J].岩石力学与工程学报,2005,24(9):1612-1618.ZHANG De-zhi,ZHANG Xiang-rong,LIN Jun-de,et al.Penetration experiments for normal impact into granite targets with high-strength steel projectile[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(9):1612-1618.
