Matlab辅助高等数学教学方法初探

夏静 卜华龙

（1 巢湖学院数学系，安徽 巢湖 238000）

（2 巢湖学院计算机与信息工程学院，安徽 巢湖 238000）

1 引言

高等数学是高校绝大部分理工科专业必修的一门基础理论课，高等数学有其固有的特点，即高度的抽象性、严密的逻辑性和广泛的应用性。传统的数学教学方式往往是一支粉笔，一块黑板以及对问题的静态描述，难以帮助学生深入浅出的理解教学内容，可能导致一部分学生失去学习兴趣和信心，从而难以取得预期的教学效果[1,2]。

提高学生兴趣、帮助学生理解抽象内容一直是困扰教师的难题，随着计算机与数学软件的发展，适当利用这类工具能改善这一问题[3,4]。Matlab是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司开发的一种数学软件，可用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。本文通过教学中一些典型问题为例，探讨Matlab在高等数学教学中的使用。

2 MATLAB图形输出功能的应用

教学时，为使学生直观理解高等数学问题，我们往往会借助几何图形讲解，然而，手工作图不准确，尤其是多维空间图形，手工示意图更是差强人意。借助MATLAB软件功能，我们通过调用MATLAB命令，就可以准确画出所需图形，从而降低教与学的难度，提高学生学习兴趣，并培养学生通过数学软件解决数学问题的意识和能力。

2.1 深化对极限的理解

极限是高等数学里的第一个重要的抽象概念，实际上，中学的数学课程里已经有一些简单的极限知识，学生往往认为只要会进行一些具体极限的计算就可以了，但若不能很好理解极限的数学定义，将对后续知识的学习产生极大的影响，比如函数连续，可导等重要概念都是建立在极限的基础之上的。若在讲解定义过程中展示出极限的“无限靠近”特征，通过几何图形则能够很好地体现其内涵，可使学生理解得更加深刻，教学效果明显提高。

在MATLAB的命令窗口中输入如下命令集合：

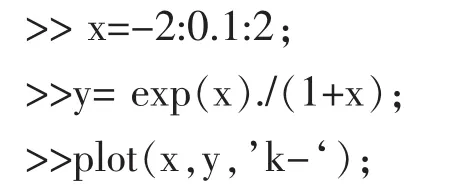
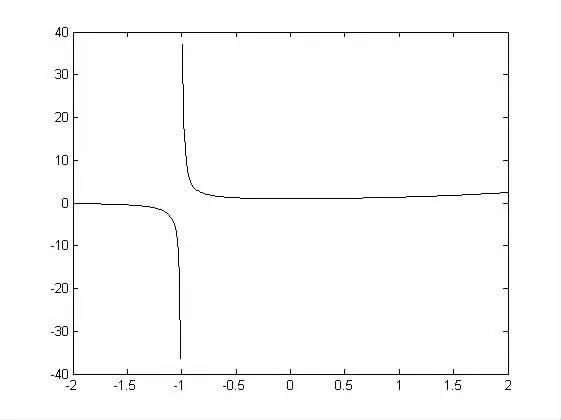
图1 极限示意图

2.2 观察函数级数展开后的逼近程度

以函数的Taylor幂级数展开为例:

若在x=a点附近进行Taylor幂级数展开，则得出：

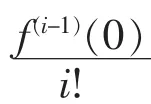
例2 对余弦函数Taylor幂级数方式展开，并观察不同阶次的拟合程度。

在MATLAB的命令窗口中输入如下命令集

特别的，当函数在x=0点附近进行Taylor幂级数展开，则得出

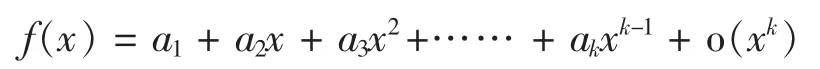
其中，每个系数ai的确定方法与前面一样，

ai＝合:

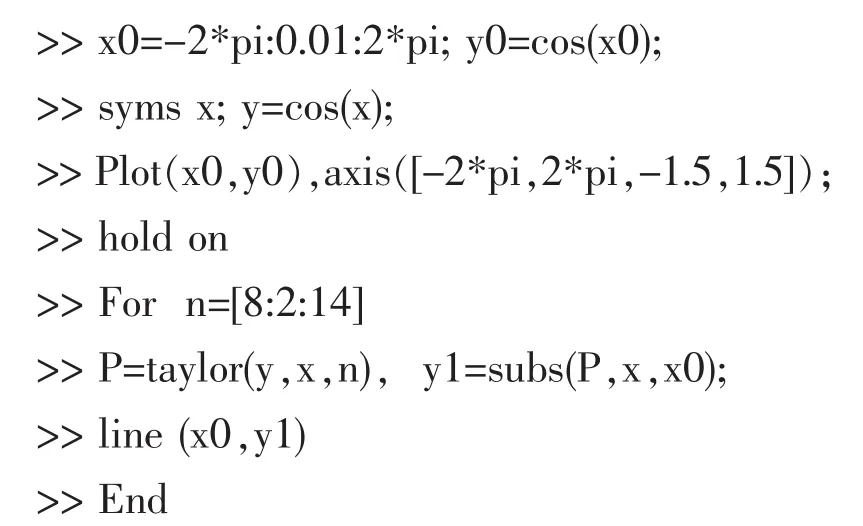
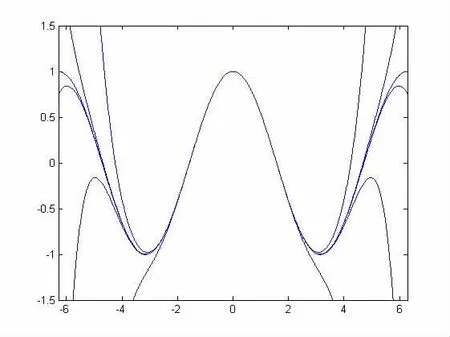
图2 各阶余弦函数拟合曲线

上图2得到了余弦函数各阶次的拟合曲线，从图中可以发现，若拟合次数低，则拟合效果较好的范围较小，若增加拟合的阶次，则拟合程度好的范围将显著增加。

2.3 帮助学生学习空间解析几何

对于传统的高等数学里的空间解析几何部分教学，学生普遍感觉学习吃力，原因是难以想象复杂空间图形，更难以作图。若能正确做出图形，学生若“真实”的看见图形，则能极大程度上提高学生理解深度，也就是说图形的有无是能否解决问题的决定性因素之一。

例3 试绘制出二元函数z=x2+y2+5的图像。

在MATLAB命令窗口输入如下命令集合：

结果图如下图3：

图3 二元函数示意图

3 Matlab强大的数值处理功能的应用

不少高等数学问题理论简单但计算量大，学生在解决这类问题时往往花费很多时间计算，却得不出正确结果，这导致部分学生对这类数学问题“望而却步”，降低学生学习兴趣。应用Matlab相关命令，就能轻松解决繁杂的计算。

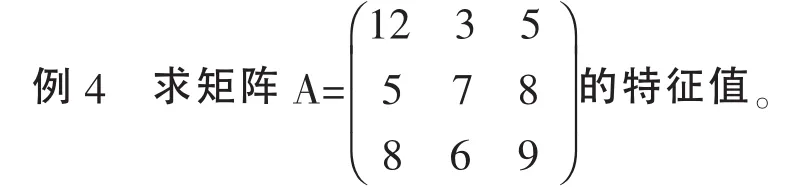
求A矩阵特征值可以直接调用MATLAB中的 eig（）函数。

在命令窗口输入：

从而立刻得到矩阵A的特征值如下：

由上可见，繁杂的计算在Matlab里只需一条简单的命令就能解决，这有助于激发学生学习数学方法和数学工具的兴趣，提高学生解决数学问题的能力，将数学的工具性作用落到实处。

4 总结和展望

除了以上列举的一些典型应用，Matlab还可以深入高等数学的很多方面。通过MATLAB形象化、具体化各类抽象问题、简单化繁琐的计算，可以提高学生学习兴趣，也能增强学生编程动手能力。既有益于高等数学教学，也有益于编程能力的开发。当前的高校各类课程教学，对教师提出了更高要求，结合各类新兴的教学工具和教学软件提高教学效果，不失为高等数学教学的一条新思路。

[1]薛定宇，陈阳泉.高等应用数学问题的MATLAB求解[M].北京：清华大学出版社，2004.

[2]郭志军.论高等数学中计算的 MATLAB 实现[J].中州大学学报，2007，24（4）：116-118.

[3]张爱华，付宏伟.MATLAB在高等数学教学中的应用研究[J].软件导报，2008，7（6）：161-163.

[4]赵亚男，牛严涛.MATLAB在解析几何教学中的应用[J].长春大学学报，2011，21（4）：54-58.