组合式成型装药数值模拟与分析*
2012-12-10王志军尹建平
孙 华,王志军,尹建平
(中北大学机电工程学院,太原 030051)
0 引言
由于爆炸成型弹丸EFP[1]的密实性较好,动能较高,攻击效果基本不受炸高的影响,从而得到广泛应用;然而环形药型罩在环形装药起爆后,在爆轰波和爆炸产物的作用下,环形药型罩挤压翻转,形成环形侵彻体,由于其开孔大、装药长径比小等特点,常用于为反舰导弹和鱼雷等串联随进战斗部的前级装药[2]。文中提出了一种组合式装药结构,即用一级主装药能够同时形成EFP和环形侵彻体,且二者之间存在一定的速度差,可以实现环形侵彻体先于EFP达到目标完成开孔任务,之后EFP随进对目标进行二次毁伤的目的。该结构能够应用于防空、反导、反武装直升机、反陆军轻型装甲和海军轻型装甲等领域。文中利用ANSYS/LS-DYNA软件对该结构进行了数值模拟,并研究了药型罩材料组合和偏移量d对该结构的影响。
1 组合式成型装药结构设计
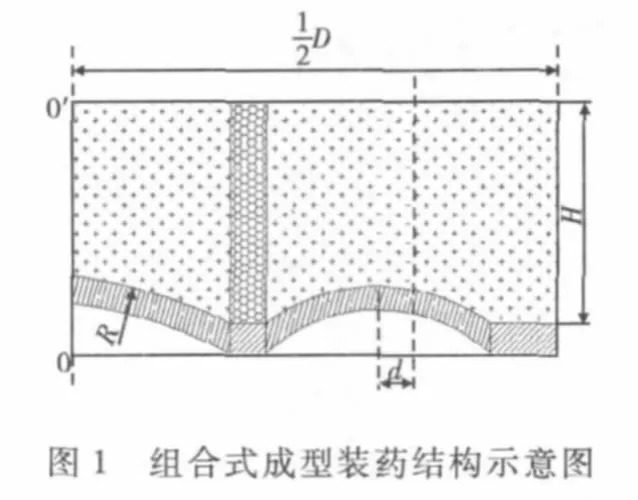
该结构主要难点在于,等壁厚环形药型罩形成环形侵彻体的过程中,由于内外罩的质量以及装药量的不对称性[3],从而环形侵彻体会发生沿轴向的偏移,进而影响其侵彻效果。为了有效降低环形侵彻体发生偏移,文献[4]和文献[5]借鉴的是等冲量设计原则,按一定比例分别对内、外罩的厚度进行调整,内、外罩底至罩顶间的厚度均匀变化,内罩底边厚需增加一定厚度,外罩底边厚需减少一定厚度,但是要使内外罩的质量和分别作用在其上的有效装药相等,从而实现内外罩的冲量相等,在工程实现上以及药型罩加工过程中比较困难。为了能够有效的解决该问题,文中所采用的方式是:中间药型罩和环形药型罩均为球缺型,从而便于药型罩加工,仅仅使环形药型罩的旋转轴与环形装药的旋转轴存在一定的偏移量d,如图1所示,从而有效的减小环形侵彻体的偏转角θ,得到稳定的环形侵彻体。文中提出的组合式成型装药结构如图2所示。

2 数值模拟
2.1 有限元模型与材料
文中采用Truegrid软件建立组合式成型装药的有限元模型,模型中单元均为solid164三维实体单元,并在边界上施加边界条件无反射约束,避免压力在边界上的反射;然后通过与LS-DYNA软件间的接口,将有限元模型导入求解器中进行计算。全文使用的单位制为:mm-ms-kg-GPa。由于该结构为轴对称结构,所以模型采用1/4网格划分,从而减少模型单元数量,以节省计算时间。数值仿真中简化为药型罩、炸药、隔板和空气四部分,其算法均采用Euler算法。
国内外对药型罩材料[6]的研究及应用进行了大量的工作,对紫铜、钽等材料都进行了研究。文中在数值模拟中药型罩材料选其中一种或两种材料组合进行对比,这两种材料均采用Johnson-Cook材料模型和Gruneisen状态方程来描述其在动力学作用下的响应行为。文献[7]中给出了紫铜和钽的主要参数,紫铜的主要参数有:ρ=8.96g/cm3,A=90MPa,B=292MPa,n=0.31,m=1.09,c=0.025;钽的主要参数有:ρ=16.6 g/cm3,A=245MPa,B=493MPa,n=0.58,m=1.04,c=0.065。
炸药选用8701,用HIGH_EXPLOSIVE_BURN材料模型和JWL状态方程来进行描述,其主要参数参照文献[8]:ρ=1.787 g/cm3,D=7.98Km/s,Pcj=29.5GP。
2.2 组合式侵彻体成型过程的数值分析
为了研究组合式侵彻体的成型过程,文中采用装药口径D=140mm,装药高度H=40mm,中间药型罩材料为钽,曲率半径为30mm,壁厚为3mm,偏移量d=2mm,环形药型罩材料为紫铜为例进行数值模拟。图3为该组合装药结构在不同时刻形成侵彻体的过程。

图3 组合式侵彻体的成型过程
由图3可以看出,在炸药起爆条件下,爆轰波首先对中间药型罩和环形药型罩的罩顶进行压垮,随着爆轰波的进一步传播以及爆炸产物的影响,药型罩两侧也开始翻转,在40μs时,中间药型罩和环形药型罩基本完成翻转,组合式侵彻体形态基本稳定,由于所受爆轰波作用时间长短的差异,头、尾部之间有一定的速度梯度,从而在40μs至60μs阶段侵彻体继续被拉伸,直至速度趋于一致。

图4 组合式侵彻体头、尾部速度变化曲线
结合图3和图4,可以看出 60μs 时中间EFP头、尾速度达到一致,80μs时环形侵彻体头、尾速度达到一致,且两者之间存在较大的速度差,环形侵彻体的速度大于中间 EFP的
速度,即可以实现环形侵彻体先于中间EFP达到目标完成开孔任务,之后中间EFP随进对目标进行二次毁伤的目的。
2.2.1 药型罩材料选取对结构形成组合式侵彻体的影响
为了研究药型罩材料对结构形成组合式侵彻体的影响,文中分别对:方案1,中间药型罩和环形药型罩均为铜;方案2,中间药型罩和环形药型罩均为钽;方案3,中间药型罩为钽环形药型罩为铜;方案4,中间药型罩为铜环形药型罩为钽进行了数值模拟。

图5 不同材料组合下侵彻体成型

表1 不同方案结果对比
结合图5和表1可以看出:当材料组合为中间药型罩为钽,环形药型罩为紫铜时环形侵彻与中间EFP的速度差达到703m/s,EFP和环形侵彻体均有较高的长径比,且环形侵彻体未发生轴向偏移;当两者材料一样时,中间EFP的速度大于环形侵彻体的速度,是因为环形炸药起爆后,爆轰波虽然受到隔板的作用,但是有一部分爆轰波通过透射,在中心轴上形成透射波叠加,如图6所示,使中间药型罩受到爆轰时间延长,从而中间EFP的速度大于环形侵彻体的速度;当中间药型罩为铜环形药型罩为钽,中间EFP的速度远远大于环形侵彻体的速度,且环形侵彻体发生了沿轴向向外的偏移。
综上所述:要想实现环形侵彻体先于EFP达到目标完成开孔任务,之后EFP随进继续销毁目标的目的,合理选择两者材料是一种有效的方式。在同一结构中,当中间药型罩材料密度大于环形药型罩材料密度时,能够使环形侵彻体的速度大于中间EFP的速度。
2.2.2 偏移量d对结构形成组合式侵彻体的影响
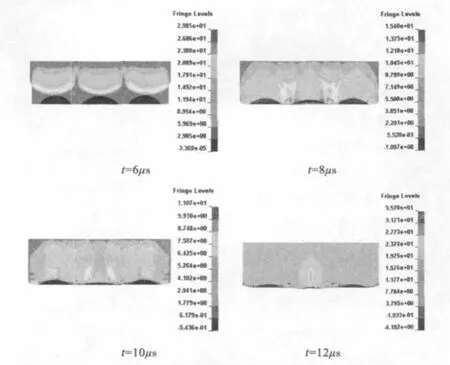
图6 各时刻爆轰波云图
为了研究偏移量d对结构形成组合式侵彻体的影响,文中分别对 d=0mm、d=1mm、d=2mm、d=3mm、d=4mm这5种情况进行了数值模拟。


图7 不同偏移量时组合侵彻体成型
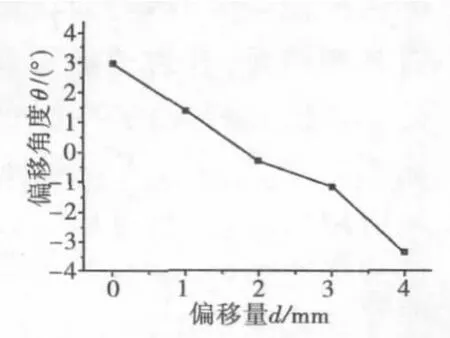
图8 不同偏移量下环形侵彻体头部偏转角曲线
从图7可以看出,当偏移量d在0~1mm之间时,环形药型罩外壁出现了大量的“崩落环”,材料利用率较低,侵彻能力将受到影响。从图8可以看出,当偏移量 d在 0~1mm之间时,环形侵彻体头部偏转角θ为正,且随着偏移量d的增大,偏转角逐渐减小;当偏移量d在3~4mm之间时,环形侵彻体头部偏转角θ为负,且随着偏移量d的增大,偏转角θ绝对值逐渐增大;当偏移量d=2mm时,环形侵彻体头部偏转角θ几乎为0°。从图9可以看出,随着偏移量 d的增大,环形侵彻体的速度逐渐增大,中间 EFP的速度几乎不变。综合图7、图8和图9可以得出:当偏移量 d=2mm时,环形药型罩内外罩所受到的有效装药相等,实现了等冲量原则,所以偏转角θ几乎为0°;当偏移量d在0~1mm之间时,环形药型罩内罩受到的有效装药多于外罩,所以环形侵彻体发生了远离中心轴的偏转;当偏移量d在3~4mm之间时,环形药型罩内罩受到的有效装药少于外罩,所以环形侵彻体发生了靠近中心轴的偏转。

图9 不同偏移量下组合侵彻体的速度曲线
3 结论
通过数值模拟表明,该组合式成型装药结构设计是可行的,能够按照预先方案在炸药爆轰以及爆轰反应物的作用下形成中间EFP和环形侵彻体两者组合式毁伤元素。并对其影响因素进行了分析,得出以下结论:
1)当中间药型罩材料密度大于环形药型罩材料密度时,能够使环形侵彻体的速度大于中间EFP的速度,从而实现环形侵彻体先于中间EFP达到目标完成开孔任务,之后EFP随进对目标进行二次毁伤的目的;
2)当偏移量d=2mm时,环形药型罩内外罩所受到的有效装药相等,环形侵彻体头部偏转角θ几乎为0°,其形态较好,侵彻能力较强。
[1]宁俊生.成型装药和爆炸成型弹丸的研究进展[J].兵器材料科学与工程,2004,27(6):65 -67.
[2]黄群涛,李铁鹏,钱建平,等.环形EFP成型及侵彻过程的数值模拟[J].火炸药学报,2009,32(5):50-53.
[3]黄群涛.环形EFP成型机理研究[D].南京:南京理工大学,2008.
[4]李永胜,王伟力,姜涛.用于串联战斗部的环形切割器优化设计[J].弹箭与制导学报,2010,30(2):93 -94.
[5]吴成,曾艳春,张向荣,等.环型聚能药型罩的设计新方法与实验[J].北京理工大学学报,2007,27(4):291-294.
[6]胡忠武,李中奎,张廷杰,等.药型罩材料的发展[J].稀有金属材料与工程,2004,33(10):1010 -1013.
[7]宋梅利,李伟兵,王晓鸣,等.药型罩材料影响EFP成型的数值计算研究[J].火工品,2009(4):16-19.
[8]高靖,王志军,范晨阳,等.中心孔对聚能装药成型的影响[J].弹箭与制导学报,2011,31(1):110-112.
