火箭发射装置回转箱体拓扑优化设计方法研究*

孙延超，李 军，韩世东，李彦君

（南京理工大学机械工程学院，南京 210094）

0 引言

回转箱体是火箭发射装置中主要的支承和传力部件，既要支承箱体内的传动部件，又要承受俯仰体由于燃气射流作用产生的冲击载荷[1]。其结构的刚强度是影响火箭发射装置可靠性与射击精度的重要因素。同时，回转箱体又是火箭发射装置中最具减重潜力的部件之一。基于传统保守设计理念设计出的结构刚强度安全系数偏大，增加了回转体质量，对发射装置回转机的机动性造成一定影响。在保证结构足够刚强度的条件下，尽量减小回转箱体质量，将有效改善火箭发射装置的整体性能。

文中将针对回转箱体最为恶劣的四种典型发射工况，采用基于变密度法的拓扑优化技术，对回转箱体进行结构优化，获得回转箱体的最优拓扑结构。在拓扑优化的基础上对回转箱体结构进行二次设计以及刚强度分析。

1 载荷工况分析

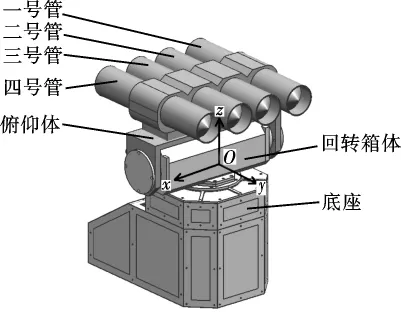
图1 发射装置整体结构

回转箱体通过耳轴与俯仰体连接，通过立轴与底座连接，箱体内装有电机、减速器等传动部件。回转箱体在火箭发射时所受的载荷分为静载荷与动载荷，静载荷为俯仰体以及传动部件自身重力及重力矩，动载荷为燃气射流冲击所造成的，燃气射流对发射装置的冲击力由俯仰体通过耳轴传递至回转箱体，再由回转箱体的立轴传递至底座。为明确说明四种典型发射工况，将发射装置的定向管、回转箱体的耳轴分别编号，发射装置整体结构如图1所示，回转箱体如图2所示。各工况载荷的测量均以图1所示固定坐标系o－xyz为基准，该坐标系原点位于回转箱体质心位置，x轴与俯仰体回转轴线平行，z与回转体回转轴线平行，y轴与x轴z轴构成笛卡尔右手直角坐标系。火箭发射过程中，底座通过地脚螺栓固定于大地上。

文中针对如下4种发射工况进行拓扑优化。

工况一：0°方向角，0°射角，一号管内火箭发射；

工况二：0°方向角，0°射角，四号管内火箭发射；

工况三：0°方向角，60°射角，一号管内火箭发射；

工况四：0°方向角，60°射角，四号管内火箭发射。

以上4种工况是相对独立的，对结构具有相同的刚度要求。每种工况下回转箱体耳轴所受y向载荷及z向载荷的最大值如表1所示。

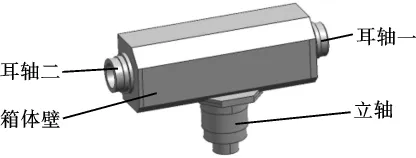
图2 回转箱体

表1 四种工况下载荷

2 拓扑优化原理

拓扑优化的主要思想是将寻求结构的最优拓扑问题转化为在给定设计区域内寻求最优材料分布问题[2]。连续体结构拓扑优化常用方法有均匀化法和变密度法，文中采用变密度法[3－4]。变密度法的思想是将连续体离散化以后，规定每个单元内部材料属性为常数，设计变量定义为每个离散单元的相对密度。相对密度是表征材料分布率的一个参量，用ηi（0≤ηi≤1）表示，单元材料物理参数随相对密度变化而变化，这种关系可表示为[5]：

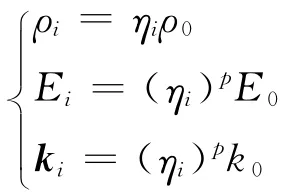
其中：ρi、Ei、ki分别为优化后第i个单元的密度、材料弹性模量、单元刚度矩阵，下标0表示优化前材料实际属性。p为惩罚因子，其作用是对中间密度单元项进行惩罚，使设计变量ηi尽可能地趋近0或1，以尽量减少结构中间密度单元的数目，从而得到清晰的拓扑结构。若结构优化区域划分为n个单元，则优化模型中设计变量为n个，即η1，η2，…，ηn。

3 拓扑优化模型

箱体有限元模型如图3所示。其中，箱体壁采用壳体单元，耳轴及立轴采用六面体单元划分网格，壳体单元与六面体单元采用节点耦合的方式连接。箱体材料弹性模量为201GPa，泊松比为0.3，密度为7.83g／cm3。箱体中耳轴与俯仰体连接部位及立轴与底座连接部位由于功能要求其结构不能改变，此部分结构在优化时定义为非优化区域，其它结构为优化区域。在两耳轴端部中心点处创建约束节点，并用刚性单元连接约束节点与耳轴内壁节点。

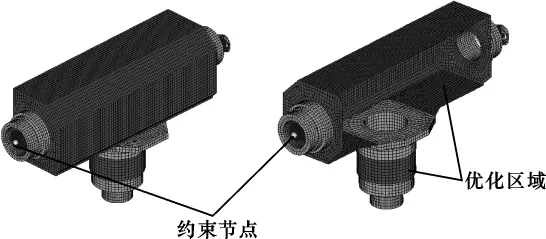
图3 回转箱体有限元模型

回转箱体拓扑优化数学模型如下：

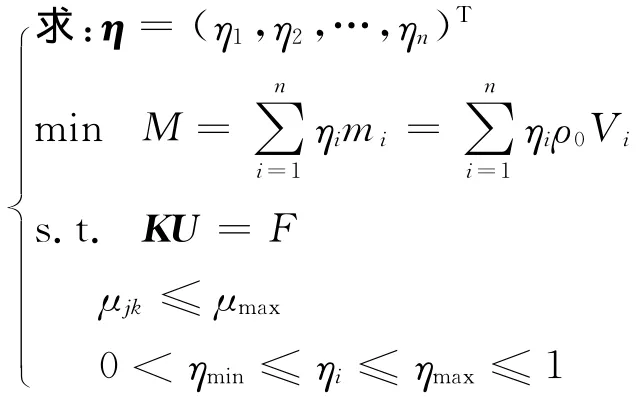
式中：η为单元相对密度向量；M为结构总质量；mi为结构第i单元的质量；ηi为第i个单元的相对密度；n为结构单元总数；ρ0为结构材料密度，K为整体刚度矩阵；U为位移矩阵；F为外部载荷，μjk为节点j在第k种工况下的位移，μmax为满足设计要求的对应节点位移，ηmin为单元设计变量的下限，ηmax为单元设计变量的上限。

4 拓扑优化结果分析

利用结构优化软件hyperworks的optistruct模块进行拓扑优化。计算经过19次迭代后收敛，目标函数及四种工况下对应约束点位移随迭代次数变化情况分别如图4、图5所示。

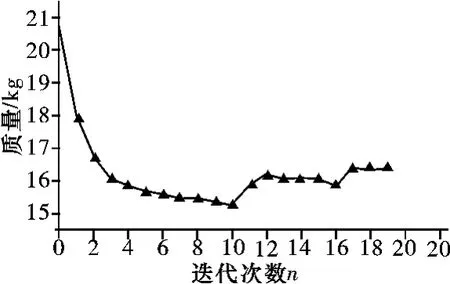
图4 目标函数迭代曲线

由图可知，优化过程中，从迭代的第1步到第10步，回转箱体质量呈单调下降趋势。约束点的位移由第9步开始有急剧上升趋势，工况一下的约束点位移在第10步超出约束值。因此，目标函数从第10步开始有所回升，工况一条件下的约束点位移逐渐向约束值靠拢。17步以后目标函数基本不变，各约束点均满足约束条件。

为清晰显示拓扑优化结果，图6是隐藏了相对密度小于0.25的单元的结构密度云图，图7为二次设计后的结构模型。

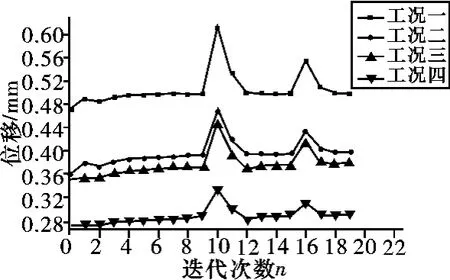
图5 约束点位移迭代曲线

图6 拓扑优化密度云图

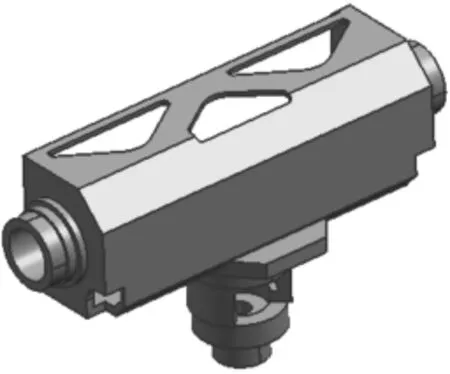
图7 优化后建立的模型

由相对密度与结构弹性模量的关系可知，相对密度越小的部位对结构整体刚度影响越小。二次设计时参考拓扑优化密度云图，将相对密度较小部位的材料去除。针对四种工况，对优化后的结构进行刚强度分析，并与优化前的结构进行对比。优化前后结构各参数对比如表2所示。由表可知，优化后的结构约束点位移有所增大，但都小于设计要求中规定的约束值0.5mm。优化后的结构整体质量减小15.4%，有效减小了回转箱体质量，达到了优化目的。文中将工况一下结构优化前后的应力分布云图展示如图8、图9所示。优化后的结构删除的部材料虽然对结构整体刚度影响不大，但具有一定承力作用，因此，优化后结构应力会相应增大。

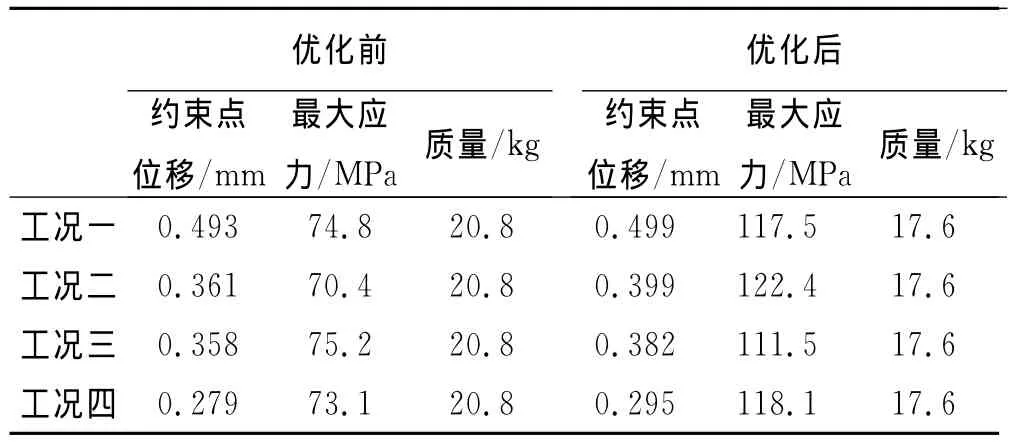
表2 结构优化前后对比分析

图8 工况一下优化前箱体应力分布图

图9 工况一下优化后箱体应力分布图

5 结论

针对四种典型发射工况，对火箭发射装置回转箱体进行了拓扑优化研究并对优化前后的结构进行了对比分析，结论如下：

1）经优化后，结构质量下降明显，刚度、强度满足设计要求。结构材料得到更为充分的利用，达到了优化目的。

2）在拓扑优化的基础上，可对结构具体尺寸如箱体壁厚再次进行尺寸优化，进一步改进结构的性能。

3）该优化方法可配合多体动力学分析法、结构有限元法等应用于火箭发射装置的其它结构设计中，对改善装置整体性能具有重要意义。

[1]吴秉贤，严世泽，龚龙兴.火箭发射装置结构分析[M].北京；国防工业出版社，1988.

[2]Fukushima J.Shapc and topology optimization of a car body with multiple loading conditions[J].SAE Technical Paper Series，1992，101（6）：1025－1029.

[3]左孔天，陈立平，钟毅芳，等.基于人工材料密度的新型拓扑优化理论和算法研究[J].机械工程学报，2004，40（12）：31－37.

[4]Bendsoe MP.Sigmund O Material Interpolation Schemes in topology optimization[J].Archive Aplied Mechanics，1999，69；635－654.

[5]王显会，许刚，李守成.特种车辆车架结构拓扑优化设计研究[J].兵工学报，2007，28（8）；903－908.