地球自转对弹道导弹射程影响的动力学分析及运动学仿真*
2012-12-10夏巍巍牟建华瞿继双傅志民
夏巍巍,牟建华,瞿继双,傅志民
(第二炮兵装备研究院,北京 100085)
0 引言
地球自转对日常生活中的低速地表运动并无显著影响,但对于飞行速度达到每秒数千米、射程在几百乃至上万公里的弹道导弹而言,则不能忽略自转对其弹道及射程的影响。通常所说的“东远西近”[1],即指导弹自西向东发射能获得更大射程,该表述是否正确、是否具有普适性,需要通过数学手段加以分析和验证。文中将对地球自转在不同弹道条件下影响弹道导弹射程的规律进行分析。
1 基于发射系的动力学分析
选取发射系作为参考系对地球自转影响进行分析。其定义如下:坐标原点与发射点固连,x轴在发射点水平面内指向瞄准方向,y轴垂直于发射点水平面指向上方,z轴与x、y轴构成右手坐标系。显然,发射坐标系为动参考系,其相对惯性坐标系以地球自转角速度ωe转动,根据矢量导数法则,发射系下的导弹质心动力学方程为[2]:

式中:v为导弹在发射系下的相对速度矢量,P、R、Fc、mg分别表示发动机推力、气动力、控制力和引力;-mωe×(ωe×r)表示离心惯性力;-2mωe×v表示哥氏惯性力。
选取正东、正西射向的两种典型弹道作为分析对象。假设两条弹道采用相同的动力系统和控制程序,则发动机推力、气动力、控制力、引力、离心惯性力均因射向相反呈对称结构,而哥氏惯性力并非如此。如图1所示,自西向东飞行时,哥氏惯性力垂直于速度指向弹道上方;自东向西飞行时,哥氏惯性力垂直于速度指向弹道下方。在哥氏惯性力影响下,两个射向的弹道并不完全对称。
可以看出,自西向东飞行时,哥氏惯性力垂直分量Fk⊥始终竖直向上,具有抬高弹道、延长飞行时间的作用,会引起射程增大;水平分量Fk∥在升弧段向西,降弧段向东,在升、降弧段飞行时间相差不大的情况下,将产生向西的位移增量,即减小射程。反之,自东向西飞行时,哥氏惯性力垂直分量Fk⊥始终竖直向下,具有压低弹道,缩短飞行时间的作用,会引起射程减小;水平分量Fk∥与自西向东飞行时一致,升弧段向西,降弧段向东,产生向西的位移增量,即增大射程。可见,哥氏惯性力水平分量和垂直分量对射程的影响是相反的,因而自转对飞行射程的影响不能一概而论,而是与弹道形状等因素有关。
选取飞行弹道的两种极限情况——竖直上抛运动和平抛运动为对象,分析自转对射程的影响。
竖直上抛运动无水平速度分量,哥氏惯性力-2mωe×v在上升过程平行于地平面指向西,下降过程平行于地平面指向东,由于竖直上抛运动上升、下降过程时间近似相等,则哥氏惯性力将引起落点处偏西的附加位移。
对于一定高程处的平抛运动,向东平抛时,抛体受到的哥氏惯性力竖直向上,将抬高运动轨迹,增大抛射距离,向西平抛时,抛体受到的哥氏惯性力竖直向下,将压低运动轨迹,减小抛射距离。显然,在相同的水平速度下,向东平抛将获得比向西更远的抛掷距离,即哥氏惯性力引起落点偏东。
综合上述分析,初始速度倾角Θ=90°时,即做竖直上抛运动的物体,在地球自转的作用下,将产生偏西的水平位移;初始速度倾角Θ=0°时,即平抛运动物体,在地球自转的作用下,将产生偏东的水平位移。对于弹道导弹,对射程起决定作用的自由段可以看作初始速度倾角在0°~90°之间的斜抛运动,地球自转对其影响将取决于具体弹道形状,从对竖直上抛和平抛运动的分析来看,其规律可能是:在较小的关机点速度倾角下,自转引起落点偏东,而随着倾角的增大,该影响将由偏东逐渐变为偏西。

图1 哥氏惯性力示意图
2 基于惯性系的运动学仿真
为了验证上述结论,本节将选取发射惯性系进行地球自转影响的分析和仿真。该坐标系的定义如下:点火时刻,坐标原点与发射点重合,x轴在发射点水平面内指向瞄准方向,y轴垂直于发射点水平面指向上方,z轴与x、y轴构成右手坐标系,该坐标系在惯性空间保持不动。
以惯性系作为参考系的优势在于,地球自转不会引起导弹受力的变化,而仅会对初始运动参数产生影响。具体而言,自转对弹道的影响主要体现在两方面:
1)地球自转使导弹具有发射点牵连初速ve,从而使弹道形状发生变化;
2)导弹飞行过程地球持续转动,将对落点经度产生影响。
本节将结合椭圆轨道理论对该影响进行分析和仿真。
2.1 椭圆轨道理论
导弹关机后,进入无动力自由飞行段,在地球为圆球的假设下,仅受到与地心距平方成反比的引力作用,将沿椭圆轨道飞行。在惯性再入方式下,若不考虑再入段气动及其它干扰因素的影响,关机点至落点的被动段弹道可采用椭圆轨道求解。根据椭圆轨道理论,椭圆几何参数及被动段射程和飞行时间均由关机点参数(rk、vk、Θk)确定[3]。
为便于表述,引入能量参数ηk及椭圆通径P:
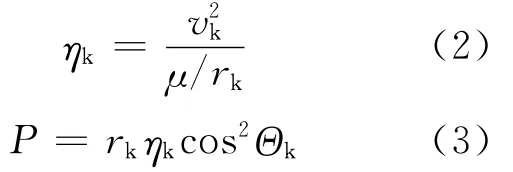
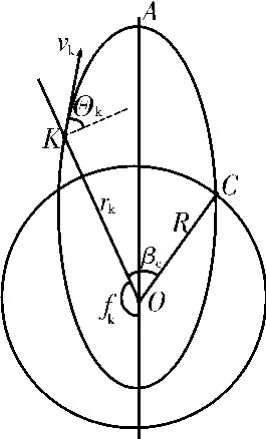
图2 椭圆轨道示意图
其中,μ为地球引力系数。
由上述关机点参数确定的椭圆偏心率为:
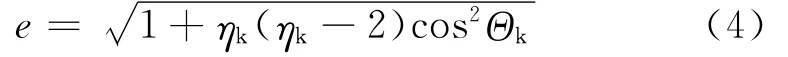
长半轴为:

被动段射程角βic满足如下二次方程:
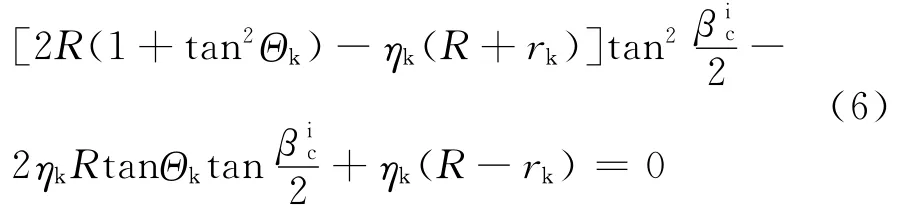
式中,R为地球半径。记:
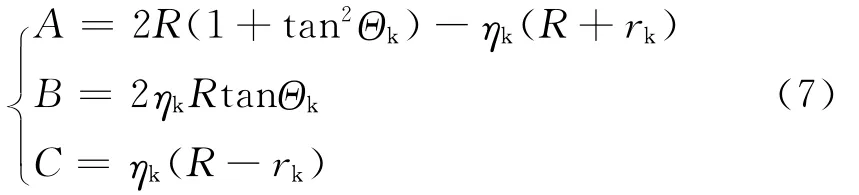
则:
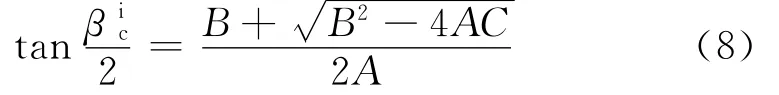
被动段飞行时间为:

已知关机点参数时,根据式(8)和式(9)可以计算被动段对应的地心角及飞行时间。需要指出的是,这里得到的地心角是相对惯性空间的,若要得到相对旋转地球的地心角,还需考虑地球自转的影响。下式给出了旋转地球表面落点经纬度及被动段射程角的解算方法[4]:
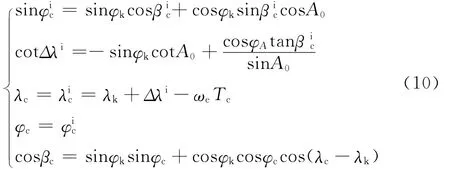
其中:ωe为地球自转角速度;A0为射击方位角;λk、φk为关机点经、纬度;Δλi为被动段相对静止地球的经度增量为落点相对静止地球的经度、纬度;λc、φc为落点相对旋转地球的经、纬度;βc为被动段相对旋转地球的射程角。此处未考虑地球扁率的影响,在地球为圆球时,被动段射程为:

将式(10)第5个方程中的λk、φk替换为发射点经、纬度λ0、φ0即可求出全弹道射程。
2.2 射程影响机理分析
弹道导弹主动段射程较短,通常只占全射程的10%以下,在小射程角范围内,水平初速对弹道高程的影响较小,由此引起的引力变化可以忽略。假设飞行程序角、发动机推力及关机时间固化,则主动段动力学过程不因地球自转而发生变化。因此,相对地球静止的情形,自转在原运动轨迹上叠加了水平初速的影响,至关机点处的速度、位置为:
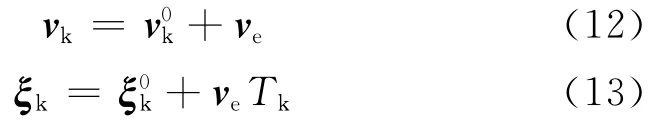
关机点运动参数的变化使被动段椭圆弹道形状发生改变,最终引起射程角及飞行时间的变化,具体可根据式(8)和式(9)计算。
另一方面,旋转地球上子午线相对惯性空间的转动也是不可忽略的,将带来落点处附加经度增量-ωe×T,其中T为导弹全程飞行时间,对该影响的处理在式(10)中已考虑。
弹道形状变化及子午线转动的综合作用决定了地球自转引起的导弹射程变化,下文将采用数值仿真方法进行分析。
2.3 数值仿真
选取惯性再入的某型号中程弹道导弹作为仿真试验原型,固化发射点位和主动段动力学过程,按照上文中分析的影响模式,计算东、西射向下的射程和飞行时间。仿真过程做了如下简化:
1)不考虑再入段气动力影响,被动段全程按椭圆轨道计算;
2)假设地球为圆球,不考虑引力谐分量的动力学影响和扁率引起的几何影响。
假设地球无自转的条件下,关机点惯性系速度倾角Θk=33°,全程飞行时间为T0,射程为L0。在地球自转的实际情形下,向东发射和向西发射的射程变化仿真结果如表1所示:

表1 某中程导弹不同射向下的射程变化情况
可以看出:在上述弹道下,向东发射时能够获得更大射程,即牵连初速引起的射程增大较之落点经度变化造成的射程损失更为显著。但该结论是否适用于其它弹道条件,还需加以考核。
为分析不同弹道条件下地球自转对射程的影响,在上述弹道基础上,固化关机点速度大小,对速度倾角进行调整,构造出不同形状的弹道序列,对地球自转条件下飞行时间和射程相对无自转情形的变化情况进行仿真计算。图3列出了自转对射程和飞行时间的影响随关机点速度倾角变化的曲线,其中实线表示射向正东、虚线表示射向正西。
可以看出,与自转同方向发射时的飞行时间长于与自转反方向发射,但在不同的关机点速度倾角下,地球自转对射程的影响量值并不相同,且随着倾角增大,极性也发生了变化。具体而言:小速度倾角条件下,与自转同方向发射能够获得更大射程,即自转引起落点偏东;随着速度倾角增大至约50°~60°,与自转反方向发射能获得更大射程,即自转引起落点偏西,该结论与基于发射系的分析结果相一致。

图3 地球自转对某中程导弹飞行时间及射程的影响
根据椭圆轨道理论,对应最大射程的最佳关机点速度倾角小于45°,因此,就发挥射程能力而言,与自转同方向发射更为有利。
3 结论
通过发射系下的动力学分析和惯性系下的运动学仿真,总结了不同弹道形状下地球自转对弹道导弹射程影响的变化规律:低弹道条件下,向东发射射程更大,而随着关机点速度倾角增大到某一临界值,向西发射将获得更大射程。但对应导弹最大射程的最佳速度倾角往往小于该临界值,因此,尽管地球自转对某条具体弹道的影响并不确定,但自西向东发射对增大导弹的最大射程能力更为有利。
[1]李桢,李海阳,雍恩米.临近空间动能武器弹道特性分析[J].弹箭与制导学报,2009,29(3):183-185.
[2]贾沛然,陈克俊,何力.远程火箭弹道学[M].长沙:国防科技大学出版社,2009.
[3]徐延万.控制系统[M].北京:中国宇航出版社,1989.
[4]沙钰,吴翊,王正明.弹道导弹精度分析概论[M].长沙:国防科技大学出版社,1995.
