基于数值仿真的火箭箭体气动特性分析*

朱和铨，张登成，屈 亮，张艳华

（空军工程大学工程学院，西安 710038）

0 引言

空中发射（空射）运载火箭技术中，箭体在高速、大攻角运动时所受到的非线性空气动力对箭－伞系统的稳定性与运载火箭的控制系统有效工作将产生较大的影响。因此，进行箭体的流体计算是空射系统的一项重要课题。西北工业大学的李易利用CFD计算了圆柱型运载火箭的下落过程中的气动特性[1]，但由于物理模型建立的过于简单，对箭体的气动力矩等不能准确的估算。文中在空中发射课题设计的运载火箭气动外形的基础上，利用CFD软件进行仿真分析，得到了空射系统的运载火箭气动力系数，为稳定伞的选取、运载火箭控制方式的设计、运载火箭的气动外形修改等提供参考。

1 理论介绍

1.1 空中发射理论简介[2]

采用前向发射，借助稳定伞来进行箭机分离和运载火箭点火前的姿态稳定与调整，当运载火箭下落到规定姿态时，启动点火程序，同时烧断稳定伞绳，运载火箭开始依靠自身携带的控制系统进行飞行控制，具体如图1所示。

图1 空中发射运载火箭过程

1.2 小型运载火箭气动外形建模

利用SolidWorks绘制的运载火箭简化平面图如图2所示（单位：m）。

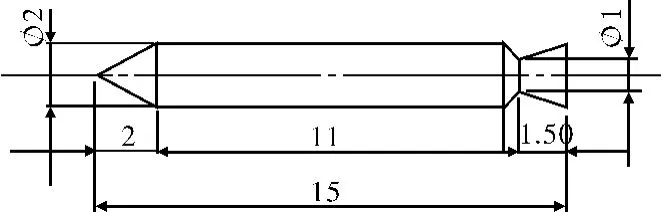
图2 运载火箭平面图

1.3 湍流模型

雷诺平均法是把湍流运动看作是时间平均流动和瞬时脉动流动的叠加，这样可以将脉动分离出来。在雷诺平均中，瞬态N－S方程里需要求解的变量已经分解为时均常量和变量。以速度为例：

同理，压力和其它的标量也可写成类似的形式：

φ表示一个标量，如压力、动能或粒子浓度等。

用这种形式的表达式把流动变量放入连续性方程和动量方程，并取一段时间的平均，就可以写成如下形式：

时均连续方程：

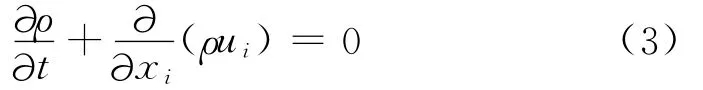
Reynolds方程[3]：

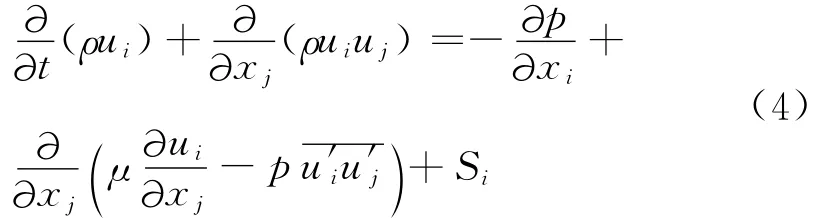
在式（3）、式（4）的基础上，再建立一个湍流动能k的输运方程，而ut表示成k的函数，从而可使方程组封闭。这里，湍流动能k的输运方程可写为：

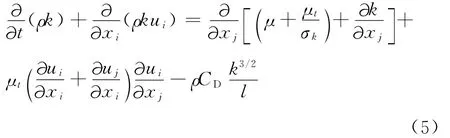
从左至右，方程中各项依次为瞬态项、对流项、扩散项、生产项、耗散项。由Kolmogorov－prandt1表达式，有：

上面几式中σk、CD、Cμ为经验常数，多数文献[3]建议：σk＝1，Cμ＝0.09，而CD的取值在不同文献中结果不同，从0.08到0.38不等。

式（5）与式（6）构成单方程模型。

2 模型建立

2.1 气条件的建立

采用国际标准大气：

1）空气被看作完全气体；

2）大气相对湿度为零；

3）以海平面作为高度技术的起点（H＝0），在海平面处，T0＝288.2K，p0＝1.0133×105N／m2，ρ0＝1.225kg／m3，根据静力学平衡微分方程[4]，可得对流层内空气温度、密度、压强随高度的变化情况。

根据空中发射初始条件，可知H＝10000m，代入可得万米高空大气参数为：T ＝ 223.2K，ρ ＝0.4127kg／m3，p＝26438N／m2。

2.2 建立数值仿真模型

由于只关心运载火箭垂直平面上的气动特点，且运载火箭是一个面对称实体。因此，为了减少计算量，选取Z轴正方向实体（图3）在Gambit软件中进行非结构网格刨分，然后导入Fluent进行数值仿真。而将仿真结果中箭体气动参数扩大2倍即为全模型的气动参数。

图3 Fluent仿真模型

湍流模型选择[5]：Spalart－Allmaras模型是一个相对简单的单方程模型，只求解一个有关涡粘性的运输方程，计算量相对较小。该湍流模型比较适合于具有壁面限制的流动问题，对有逆压梯度的边界层问题能够给出很好的计算结果，常常用在空气动力学问题当中，例如飞行器、翼型等等绕流流场分析。

流动方程采用二阶迎风格式差分，湍流方程采用二阶迎风格式差分，全显式耦合求解。

3 结果分析

3.1 气动力数据的拟合

根据运载火箭在与载机分离前后的特点，选取迎角10°时为计算初始状态点；由于运载火箭自由下落的时间一般在10s内，且具有初始水平速度209m／s，可知运载火箭的迎角不会大于130°，不失一般性，选取迎角135°为最后计算状态点。以每增加迎角5°为一个新状态点，总计计算27个状态点。

在采用4个Intel（R）Xeon（R）CPU（3.00GHz主频，2G内存）计算单元并行运算的情况下，每个状态平均在30h后达到预定的收敛值。表1为收敛后每个状态点对应的力系数与力矩系数值。

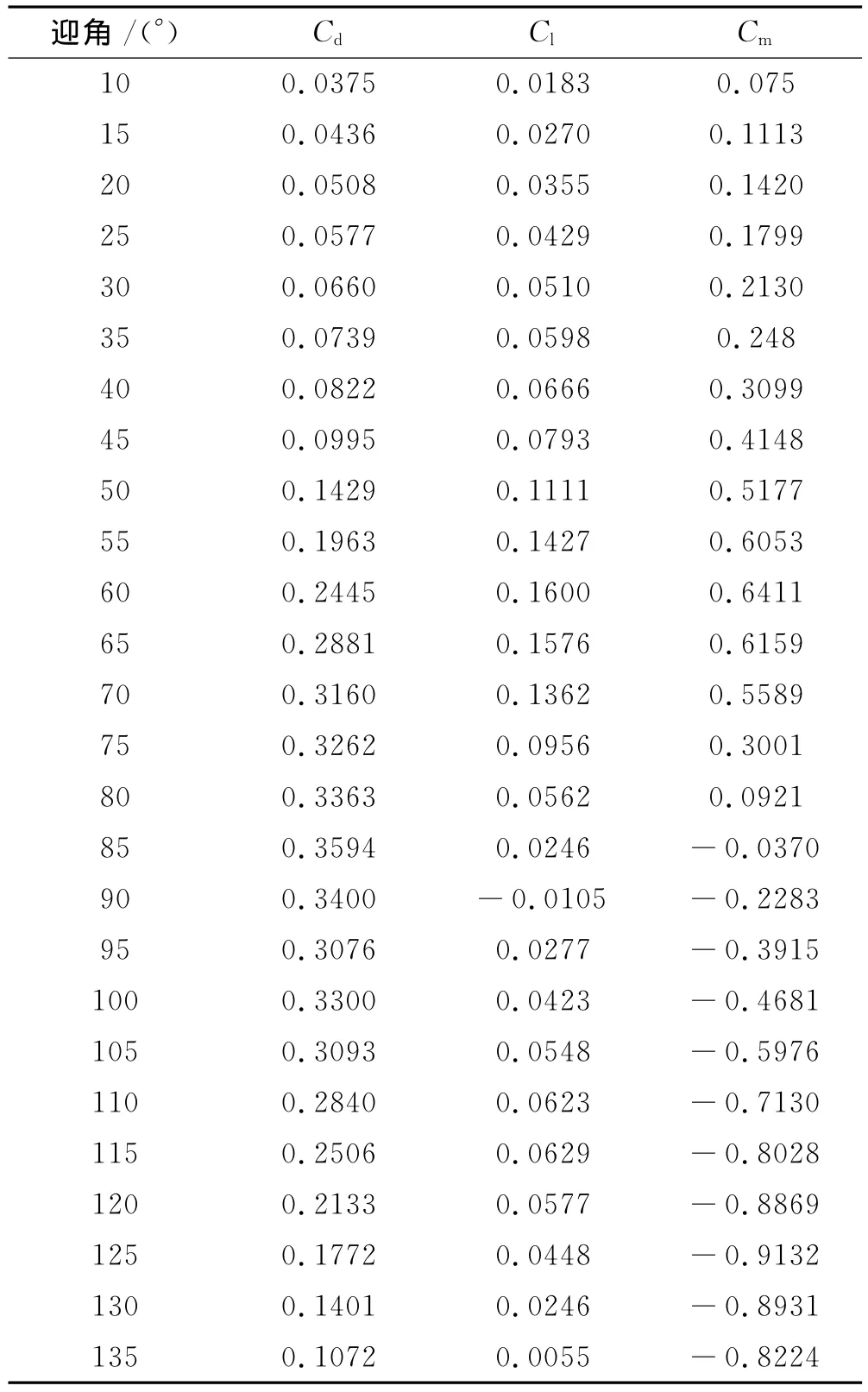
表1 运载火箭气动力参数

将表1中的计算结果导入Matlab软件中进行数据拟合，利用一维插值函数法即可得到较为准确的各个角度的气动参数。结合Reference Values中预设的参考面积（S＝27m2）、力臂均值（L＝1m）、空气密度（ρ＝0.4127kg／m3）和实际来流速度即可计算出运载火箭的气动力及力矩。

3.2 箭体的压力分布及周围涡流分析

选取迎角为10°、30°、50°、70°、90°、110°时的6个状态点压力云图进行比较分析，如图4所示。

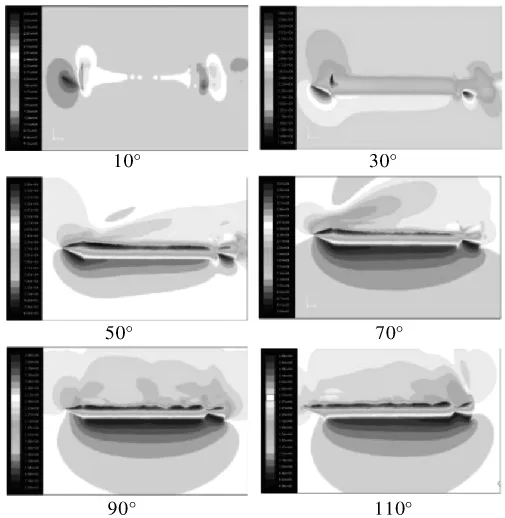
图4 不同方向来流时的压力云图

比较各个不同状态点的压力云图，可以看到刚开始时气流在运载火箭的头部和尾部背风部位有小范围的分离，形成低压区，而在迎风区域形成高压区，并且以箭头部位较为明显，随着迎角的增大，气流在运载火箭表面的分离区域逐渐从头部向尾部扩散，直至全箭体气流分离，形成严重扰流。分析压力云图变化特点，可以得出以下结论。

1）随着迎角的增大，运载火箭所受到的气动力的焦点后移，且趋势明显。这种变化的好处是：开始焦点位于重心之前，有利于运载火箭初期快速调整姿态，当快到达预期点火姿态（运载火箭接近竖直），焦点的快速后移，产生与角速度反方向的力矩，迫使运载火箭稳定。可见尾喷管的存在虽然增大了运载火箭的空气阻力，但却对系统的稳定起到很大作用。

2）自始至终，运载火箭头部与尾部均存在气流分离，形成非定常的涡流区域，因此选用空气舵进行运载火箭的姿态控制方式是不可取的。

3）裸露的尾喷管迎风面受空气压力大，因此结构设计时应当充分考虑尾喷管壁面强度。同时，如果选用矢量喷管进行运载火箭姿态控制，应当在控制系统设计时考虑执行机构能抵御喷管所受到外界强气压的影响。

3.3 箭体尾流分析

选取迎角为45°、90°时的两个状态点的流场轨迹图进行比较分析，如图5所示。

图5 流场轨迹图

由图5可以看出，运载火箭在流场中会产生较大范围的尾流区，特别是迎角90°的状态点，形成严重扰流。如果选用稳定伞来调整运载火箭姿态，考虑稳定伞的正常工作，应当尽量避免其落入运载火箭引起的尾流区域。结合稳定伞工作特点，图中选取两个白色标记点，这两个区域的流场受运载火箭尾流影响已经较小，能够保证稳定伞正常工作。比较运载火箭的外形尺寸，可知运载火箭与稳定伞之间的连接绳不应当小于20m。

4 结论

利用CFD技术，对空射运载火箭系统中箭体在不同迎角下的流场进行了数值仿真，得到了运载火箭以迎角为自变量的气动系数；分析箭体周围的流场特点及箭体表面压力分布情况，为运载火箭姿态控制方式的选择提供了参考依据；通过运载火箭的尾流分析，为以稳定伞为运载火箭初期姿态稳定方式的设计提供了连接绳的长度限制。仿真实验只进行了单独运载火箭大迎角流场特性分析，有载机和稳定伞的流场则需要进一步研究。

[1]李易.内装式空射运载火箭箭机分离动力学研究[D].西安：西北工业大学，2009.

[2]张登成，闫杰，张久星.内装式空射运载火箭与载机的分离研究[J].弹箭与制导学报2009，29（5）：158－161.

[3]王福军.计算流体动力学分析——CFD软件原理应用[M].北京：清华大学出版社，2004.

[4]陈廷楠.应用流体力学[M].北京：航空工业出版社，2006：18－23.

[5]于勇.FLUENT入门与进阶教程[M].北京：北京理工大学出版社，2008.