高层建筑框架结构与基础地基共同工作的半解析自由振动分析

谢向东

(襄樊学院 建筑工程学院，湖北 襄阳 441053)

高层建筑框架结构与基础地基共同工作的半解析自由振动分析

谢向东

(襄樊学院 建筑工程学院，湖北 襄阳 441053)

将高层建筑框架结构与其基础等效连续化为一个半无限大弹性地基上的闭口薄壁筒体，并以此三维模型，用半解析法对其动力特性进行计算. 计算结果表明：简化模型合理，分析方法正确，为高层建筑框架结构的自由振动计算提供了一种合理可行的简化计算方法，并得出了一些结论.

高层建筑；框架结构；自由振动；闭口薄壁筒；半解析法

近些年来，随着城市化建设与房地产的发展，在内陆城市的软土地基上修建高层建筑已是相当普遍. 而在高层建筑结构的选型上，由于框架结构(图1)在传力、抗震、抗侧刚度和发挥材料特长等方面具有很强的优越性，且具有良好的技术经济指标，所以框架结构在高层建筑结构中得到了很好的应用. 然而，高层建筑在设计阶段都要进行动力计算(风荷载、地震作用等)，这个计算工作量通常很大，目前很多设计院还是采用刚性地基进行计算而且输入的地震波也有局限性，计算结果一般不够准确. 为了给框架结构寻求适合初步设计阶段或整体性能评价阶段的快速、简化分析方法，本文将高层框架结构与其基础等效连续化为一个半无限大弹性地基上的薄壁筒，并以此三维模型，用半解析法对其动力特性进行了计算. 通过计算结果分析，得出了一些很有价值的结论.

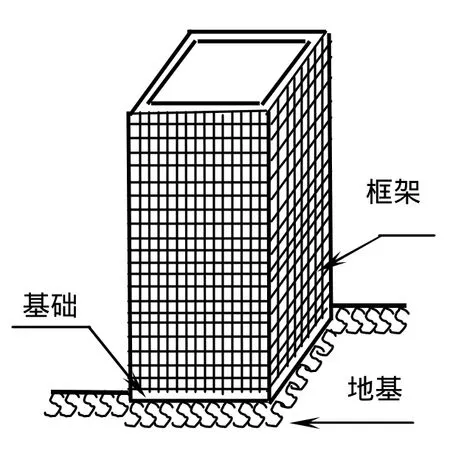
图1 框架结构示意图

1 框架结构的分析模型

本文将采用集地基、基础、上部结构为一体的三维一体化模型进行分析.对于地基，按某种综合等效弹性地基处理，也就是根据实际情况，将基坑底部与坑壁等效成不同的半无限弹性体. 对于基础，把它看成是上部结构的一部分，实际上，基础是上部结构向地下的延伸. 对于上部结构，利用刚度等效原理[1]将其等效连续化成闭口薄壁截面筒，这样就可以用三维模型对这种结构进行有效的简化计算.

在推导上述半无限大弹性地基上的闭口薄壁筒共同工作的自由振动数学模型时，取纵向节线(图2)的未知函数为基本未知量，沿周线方向半离散化，也就是在节线之间用插值函数，将整个结构的运动场表示为以节线未知函数为未知量的函数集合. 再通过哈密顿原理导出该结构自由振动的数学模型.

以下就自由振动的数学模型进行推导.

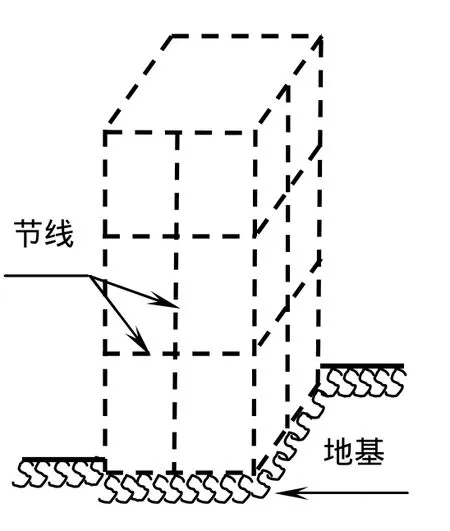
图2 薄壁筒示意图

2 控制方程的推导

为了便于描述结构的位移，作如下假定：1)刚性楼板假定，即认为楼层在其自身平面内是无限刚性的；2)楼层横截面的环向正应力与纵向正应力相比可以忽略不计的假定，即认为薄壁筒筒壁在以纵向正应力s，纵向及横向剪应力t的平面应力状态下工作.

在上述假定下，取节线的纵向位移 wi( z)为基本未知函数，节线之间用插值函数 fi( s). 于是，薄壁筒的运动场可表示为：

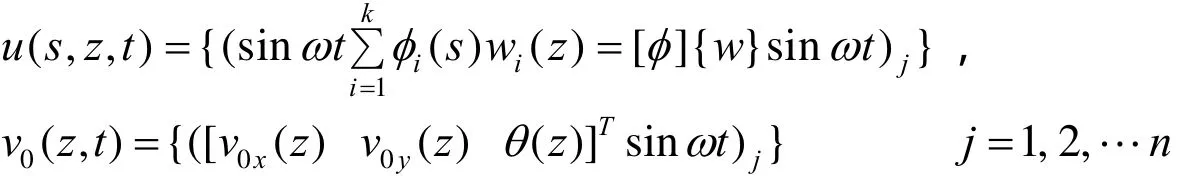
其中，z和s分别表示薄壁筒筒壁的纵向(轴线方向)与环向(截面中心线方向)，u( s, z, t)为描述薄壁筒筒壁纵向翘曲的运动函数，v0( z, t)为描述薄壁筒横截面形心横向运动的函数，它们都是函数集合. k为节线与s的交点数，n为节线在纵向的分段数.

因此，可得整个薄壁筒结构系统的总势能：P = Ut+ Utc+ Utd. 其中，Ut为薄壁筒体的弹性应变能，Utc为基础基坑周围地基中储存的弹性应变能，Utd为薄壁筒体底部地基中储存的弹性应变能，分别为：

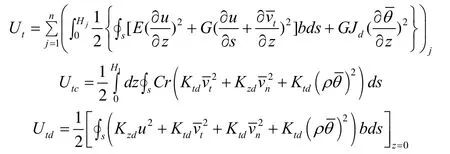
整个薄壁筒结构系统的总动能：

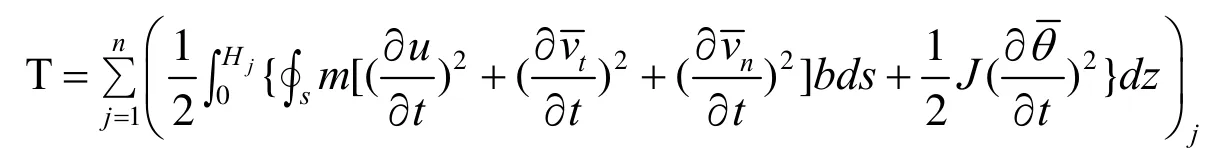
式中，E—薄壁筒体材料的抗拉压弹性模量；G—薄壁筒体材料的抗剪弹性模量；GJd—薄壁筒体横截面的抗扭刚度；b—薄壁筒筒壁厚度；vt—薄壁筒筒壁微元在局部坐标系中的切向位移；vn—薄壁筒筒壁微元在局部坐标系中的法向位移；q—薄壁筒筒壁微元在局部坐标系中的转角；Ktd—基坑底部切向的等效刚度；Kzd—基坑底部法向的等效刚度；Cr—基础与地基的接触系数；r—薄壁筒筒壁微元离横截面中心的距离. 其它符号的意义参见文献[1].

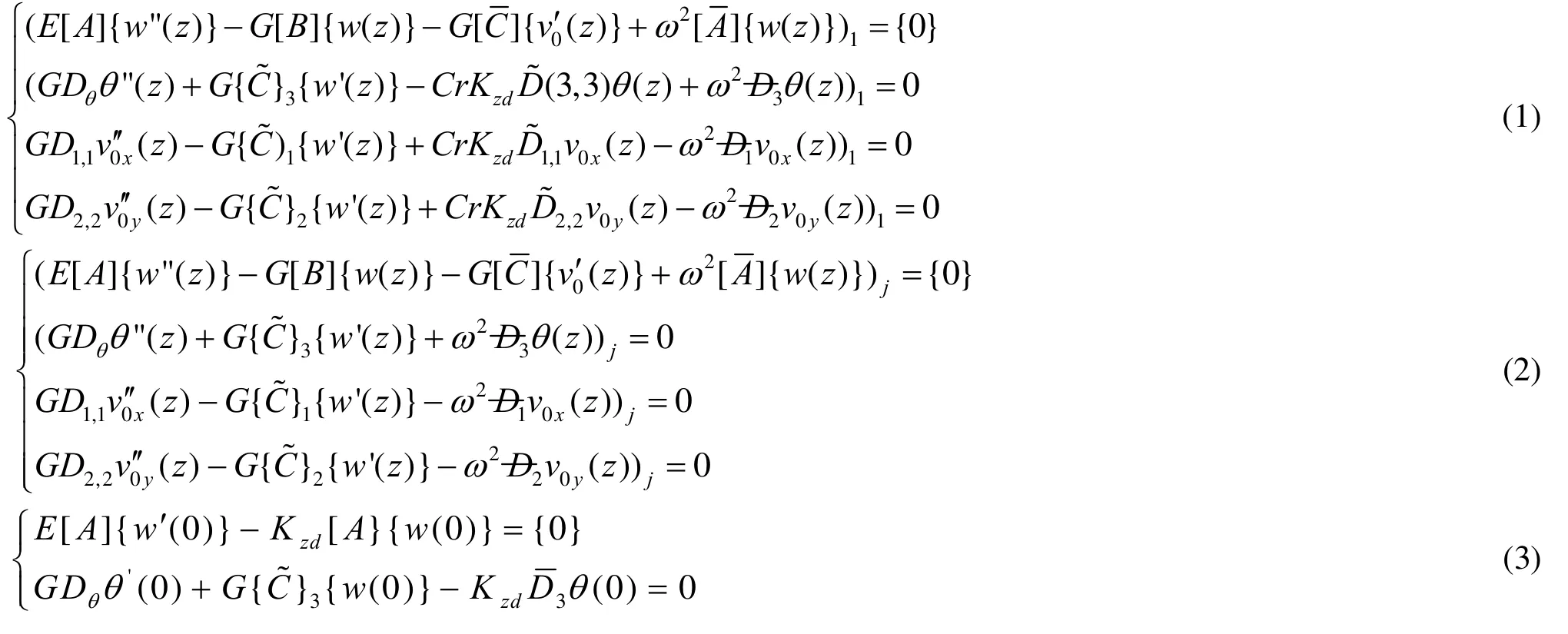
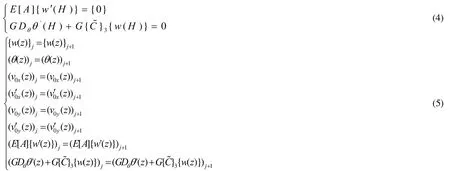
式(1)、(2)分别是关于基础、上部结构的控制微分方程，式(3)、(4)、(5)分别表示结构底部、楼顶以及结构系统各部分连接处的边界和连接条件.

以上方程组用Fortran语言编成计算机程序，在程序中调用高质高效的常微分方程求解器COLSYS[2]进行求解.

3 算例与计算结果分析

算例 高层框架结构的计算简图如图 3所示，建筑高度为 60m，长、宽均为30m. 框架柱间距为6m，梁间距为3m，截面均为0.5×0.5m2. 钢筋混凝土弹性模量E=3.25×107kN/m2，G=0.45E. 基础底部、侧面的地基压缩模量分别为Kzd=rd25.0×106kPa，Ktd=rd18.0×106kPa，Kθ=rd18.0×106kPa，rd为由场地情况确定的系数，Cr为基础与地基的接触系数(本例取 Cr＝0.5)，重力荷载取50kN/m3.

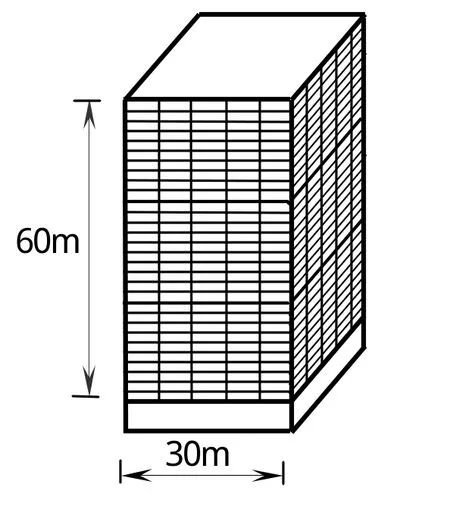
图3 算例计算简图

表1、表2、表3为部分计算结果.

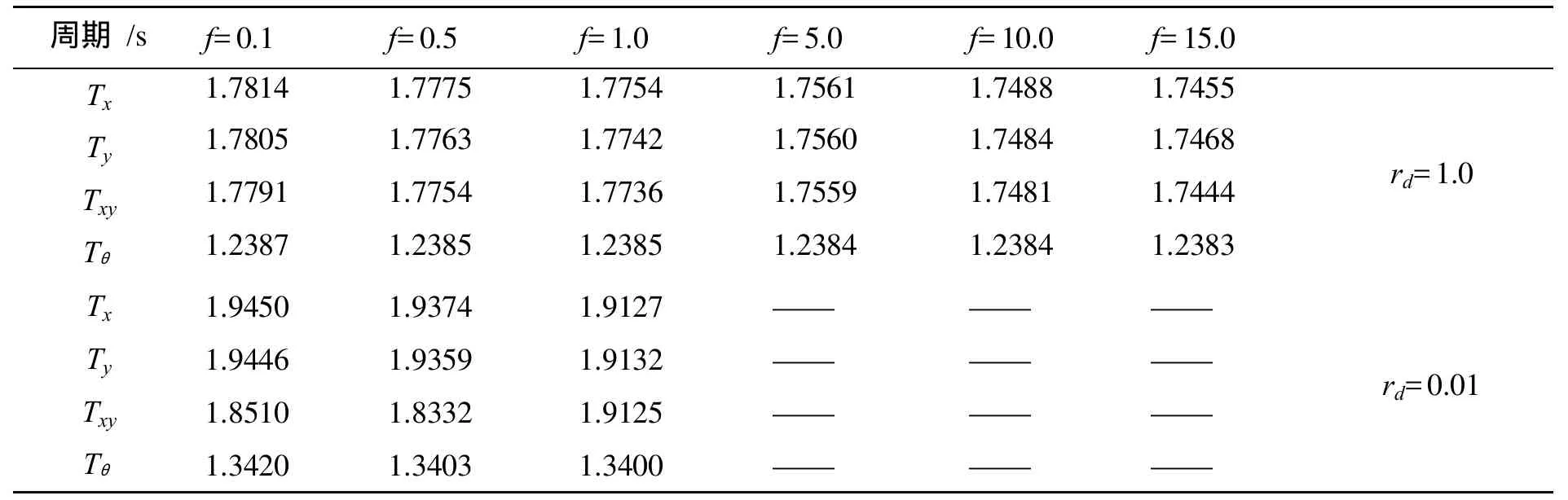
表1 基础刚度变化时结构第一自振周期的变化

表2 地基刚度变化时结构第一自振周期的变化

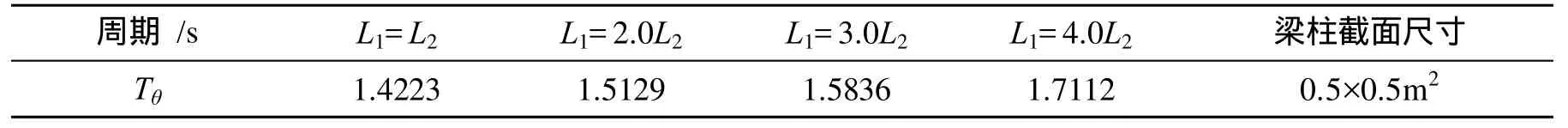
表3 横截面尺寸改变时第一扭转自振周期的变化

4 结论

1)这种方法可以对任意大型的框架结构进行高速高效的简化计算，得出比较精确的计算结果，这是其他有限元方法所无法做到的.

2)由表1可看出：随基础刚度增加，各方向自振周期逐渐减小. 但当基础刚度远大于地基刚度时，则会出现自振周期无限长(即切入)的现象. 可见在工程中，最好是地基、基础刚度都比较大且比较接近，这样二者才能协调变形，共同工作.

3)由表2可看出：当基础刚度保持不变时，地基刚度有一个临界值，其相对临界值增加或减小各方向自振周期都逐渐减小，只是当地基刚度减小到一定程度时，各方向自振周期则显著增大.

4)由表1、2、3可看出：地基、基础刚度变化对扭转自振周期几乎无影响，但是结构系统横截面尺寸的改变对其影响很明显，且随着结构横截面不对称性的增加扭转自阵周期显著加长，所以在抗震设防中应该通过调整结构系统横截面尺寸来调整扭转自振周期.

[1] 龚耀清.弹性地基上高层建筑结构及半解析法研究[D].北京: 清华大学, 1999.

[2] 袁 驷.介绍一个常微分方程边值问题通用程序—COLSYS[J].计算结构力学及其应用, 1990(2): 104-105.

[3] 包世华, 周 坚.薄壁杆件结构力学[M]. 北京：中国建筑工业出版社, 1991.

[4] 谢向东. 高层建筑框架结构与地基基础共同工作的半解析静力分析[J]. 襄樊学院学报, 2011(2): 12-15.

[5] 谢向东. 地基基础刚度变化对超高层束筒结构的影响[J]. 西安建筑科技大学学报: 自然科学版, 2008(2): 184-188.

[6] 谢向东. 地基基础刚度变化对超高层建筑自振特性的影响[J]. 西安建筑科技大学学报: 自然科学版, 2007(3): 402-410.

(责任编辑：饶 超)

Analysis on Free Vibration by Semi-analytical Approach for Collaboration of Frame Structure of Tall Building and Foundation

XIE Xiang-dong
(School of Civil Engineering and Architecture, Xiangfan University, Xiangyang 441053, China)

In the paper, the superstructure and its foundation of a tall building frame structure are simplified equivalently and continuously to a three-dimensional model, which is a combination of thin-wall tubes on semi-infinite elastic subgrade. And its dynamic characteristics are computed with the three-dimensional model by semi-analytical approach based on ODE(Ordinary Differential Equation) Solver. It is observed from the computing example that the new method is reasonable and feasible, At the same time, some valuable conclusions are obtained through analyzing the reasonable results of the numerical example.

Tall building; Frame structure; Free vibration; Closed thin-wall tube; Semi-analytical method

TU973

A

1009-2854(2012)02-0005-04

2012-02-11

襄樊学院博士基金项目

谢向东(1975— ), 男, 河南南阳人, 襄樊学院建筑工程学院讲师, 博士, 主要研究方向: 高层建筑结构的分析与研究.