基于Matlab实验的非局部反应扩散逻辑方程解的进一步数值研究

李 珊 孙丽男

（黑河学院 数学系，黑龙江 黑河 164300）

基于Matlab实验的非局部反应扩散逻辑方程解的进一步数值研究

李 珊 孙丽男

（黑河学院 数学系，黑龙江 黑河 164300）

论文主要考虑如下形式的非局部问题

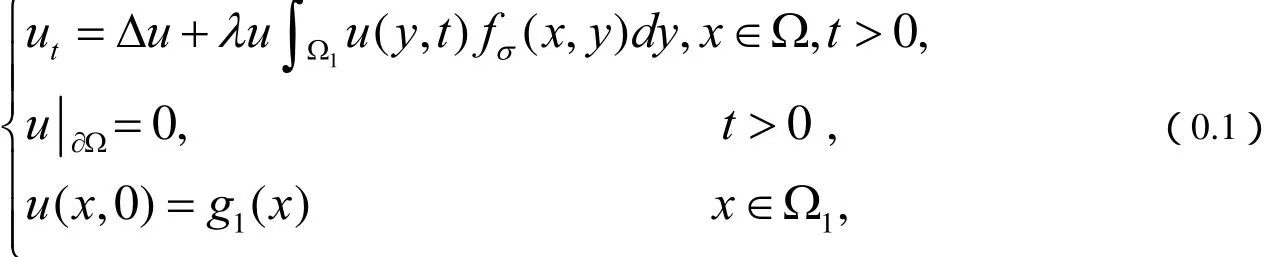
其中

1.若 π2/4

λ＜n ，上述问题有一个稳定的平衡解u=0；

2.若 π2/4

其中n=1,2,…，从而为进一步研究非局部问题的解析解奠定基础。

非局部反应扩散方程；数值实验；平衡解；稳定性；分歧

1 引言

伴随着科技和社会的发展，人们越来越关注与人类生存息息相关的环境和生态研究，而作为生态学分支的人口动力学在自然界的各个领域都有着广泛的应用，通过人口动力学的研究，人们可以更好地认识和了解自然模式的形成和发展，见[1,2,3]，局部反应扩散方程恰恰成为人们研究过程中的一个经典之作，其有如下形式[4]：

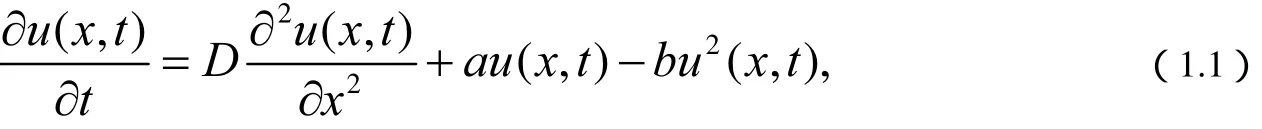
在[4]及许多文献中，对于（1.1）的平衡解的研究已经很充分了，因此我们更加关注的是上述经典方程的推广形式[5]

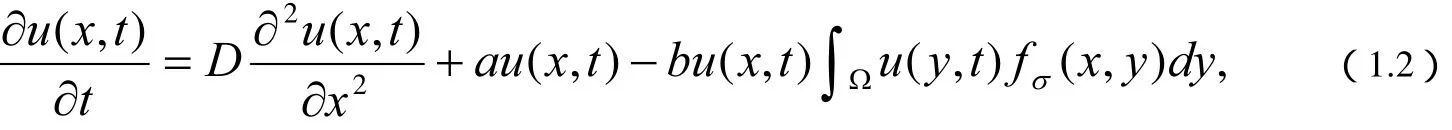
在[6]中，我们已经对简单的非局部问题的解进行了数值分析，[6]中讨论的问题的非局部影响区域是一个确定的区间，即非局部项中得积分区间是一个确定的闭区间，这就使得无论是数值实验还是解析研究都容易了很多。若积分项的积分区间与变量x有关，则相应的非局部问题就变得复杂了，也更贴近实际生活了，值得我们进行进一步的研究。

本文中，我们考虑以下非局部问题

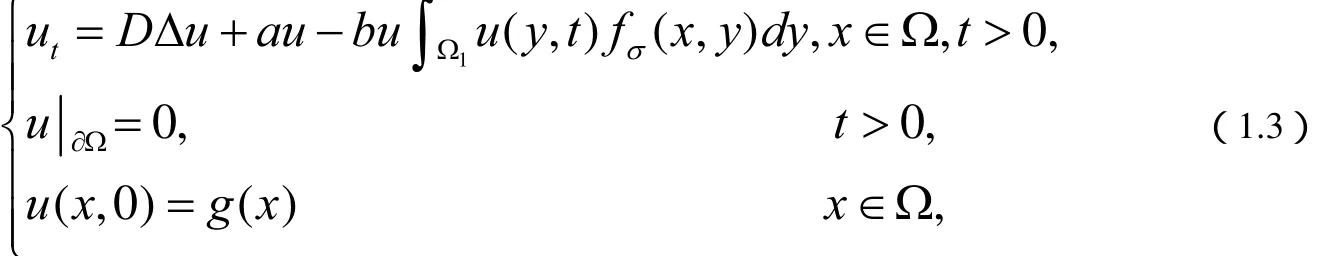
其中

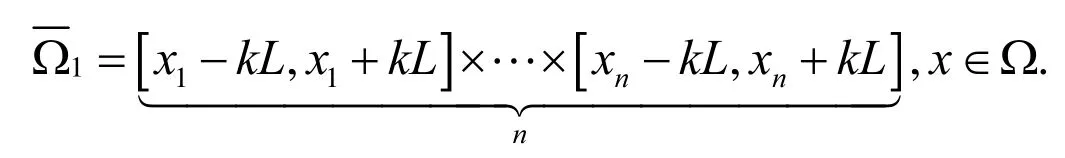
我们首先考虑n=1的情形

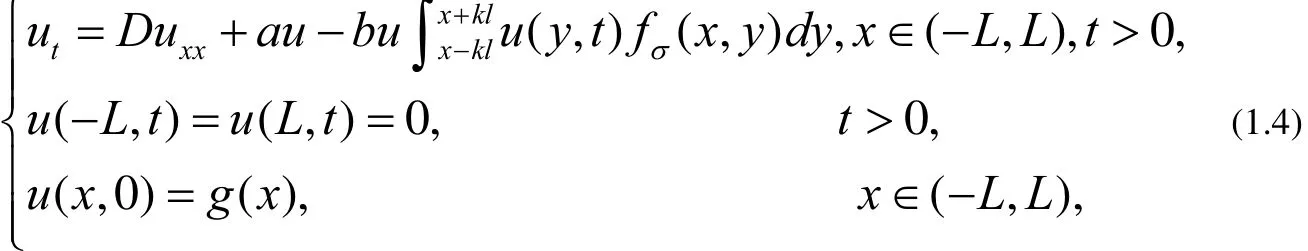
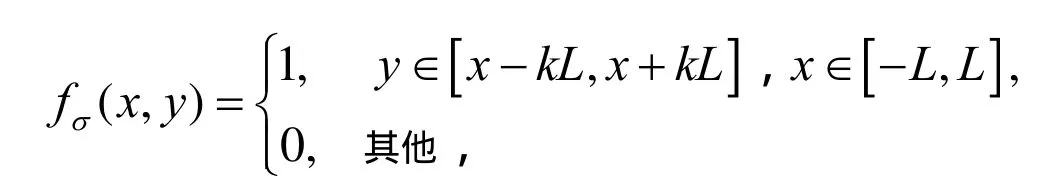
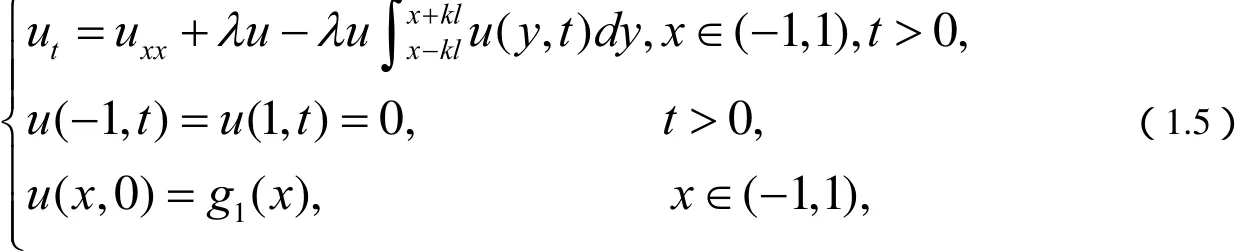
2 数值实验及主要结果

2.1 数值实验

本部分，我们将简单介绍采用的数值方法以及实验方法。

在这里，我们采用的数值方法仍然是简单有效的有限差分法[]7。采用数值方法研究问题的关键是对区域、方程的离散以及对边值条件和初始条件的处理。

2.接下来我们采用向前差分格式对方程

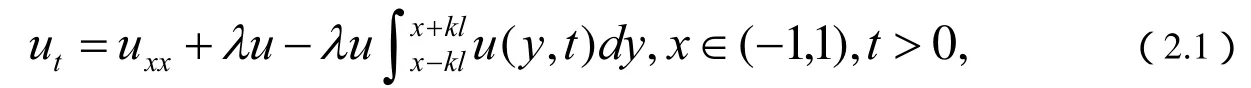
进行离散，得到

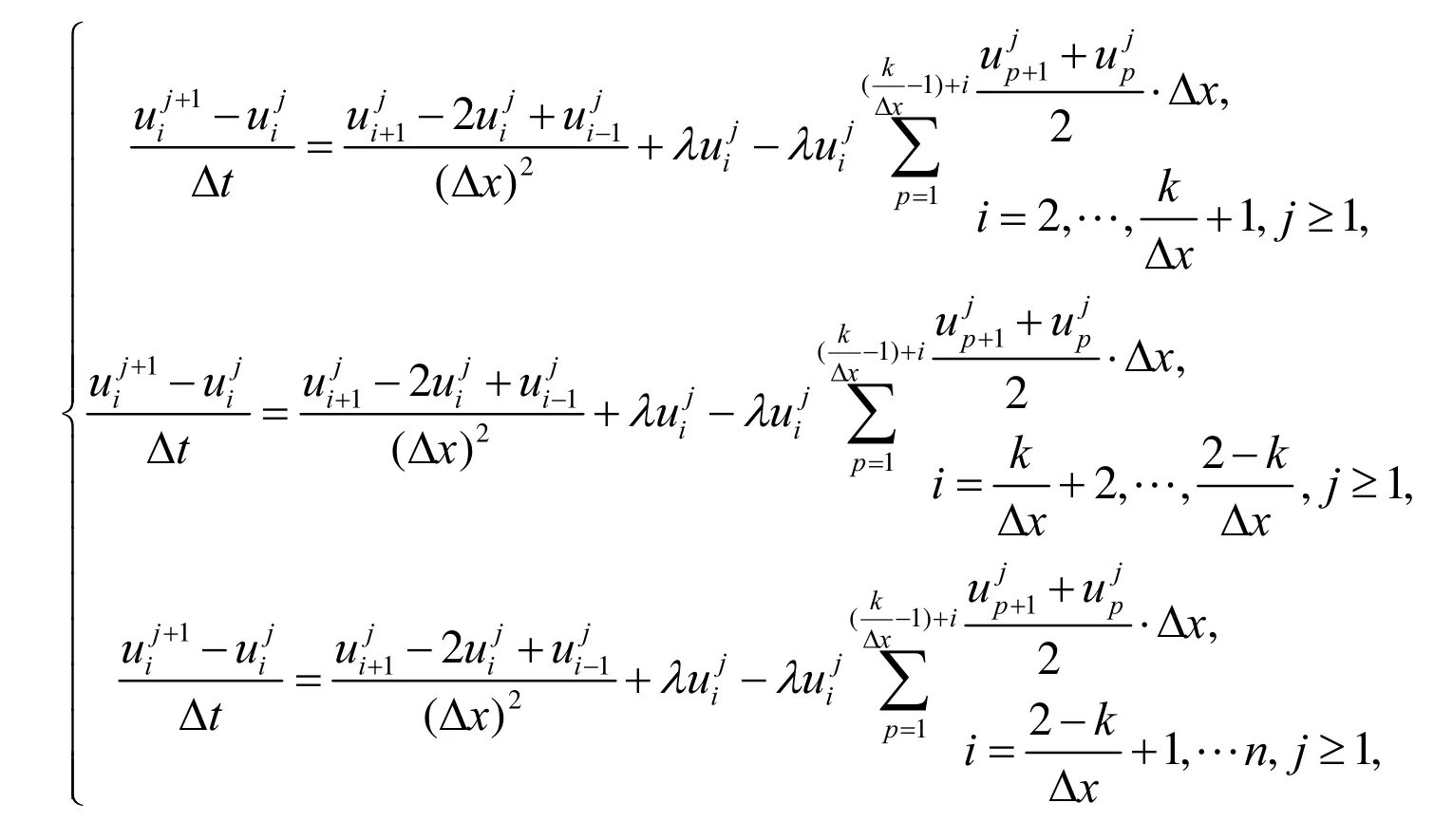
（2.2）3.初值条件的处理

4.边值条件的处理

下面我们将利用Matlab做一些数值实验来研究（1.5 ）平衡解的状态，不失一般性，我们在（1.5 ）中取k=0.3，考虑下面的狄利克雷问题

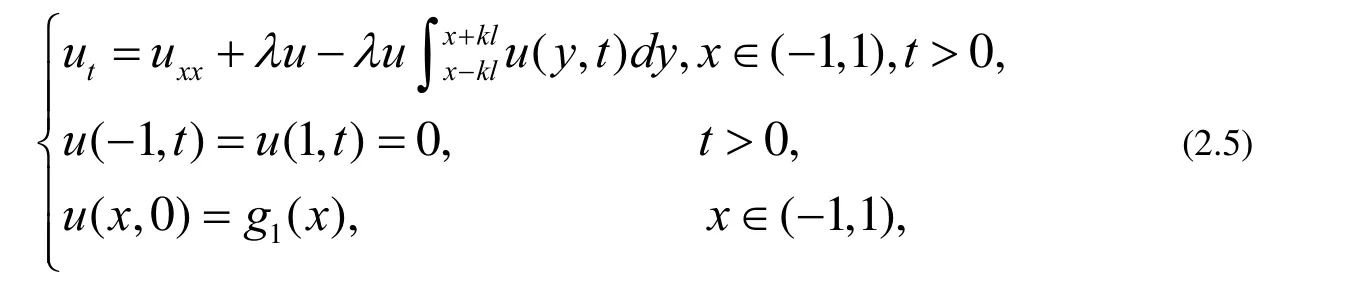
我们采用上面阐述的数值方法，并取 Δx =0. 1, λ= 1以及 g1( x)=1-x2。在实验中我们发现，首先（2. 5 ）的解的图像从t=0时刻的初始图形下降为t=0.1时刻的图形 （见 图1（ a）和（b）。接下来，随着时间的发展，我们观察到一系列下降的拱形，最终，当时候足够长时，它们归于一条与x轴重合的直线 （见图2（a）和（b））

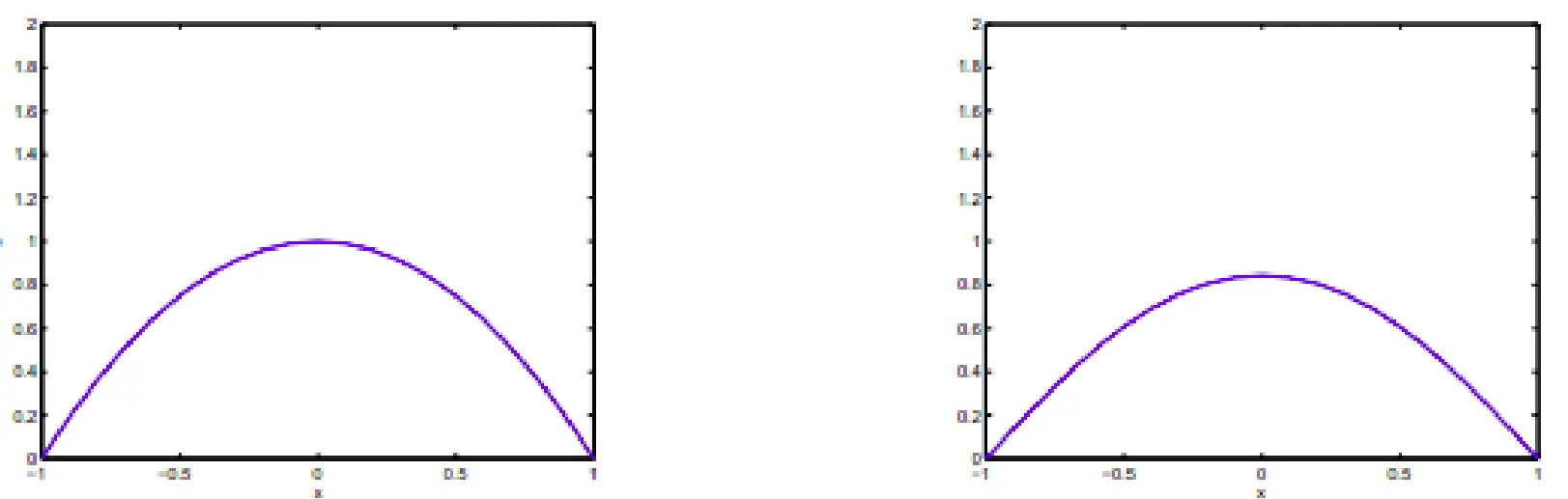
图 1a.（左） t = 0,λ= 1,u(x,0)=1-x 2 时 （2. 5 ）解的图像；b.（右）t= 0.1,λ = 1,u( x ,0)=1-x2时（2. 5）解的图像

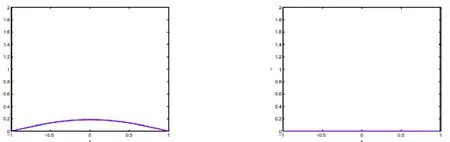
图 2a.（左） t = 1,λ= 1,u(x,0)=1-x 2 时（2. 5 ）解的图像；b.（右）t = 15,λ = 1,u( x ,0)=1-x2时（2.5）解的图像

在上述实验中，我们取λ=1，它小于π2/4，接下来，我们考虑 π2/4 λ＞ 时的情形，之所以选π2/4这样一个临界数是从方程结构特点得到的，在接下来的实验中，我们取λ=10，它比 λ= π2/4要大，同时我们选取两组不同的初值 u (x ,0)= 1- x2和 u (x,0)= g(x)其中

3

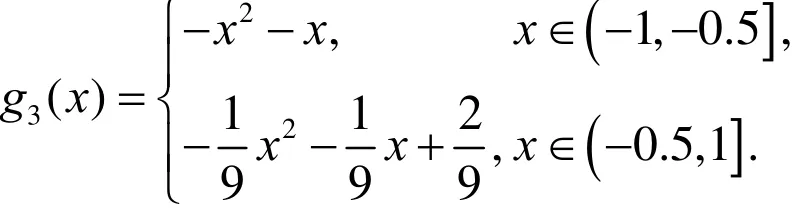
在实验中，我们发现当经历比较短的一段时间后，对应第一种初值解的图像如图（图3a），对应第二种初值，解的图像如图（图 3b）。从上述图像上看，我们很难判断随着时间的推移会发生什么样的变化！于是，我们继续实验，取t=15，这时我们发现对应两种初值的解得图像几乎一样，如图（图4（a）或（b）.当然，我们可以选取其他的初值，效果仍然是一样的如图（图4a或b）

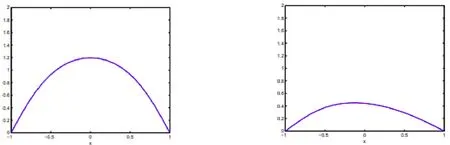
图3a.（左） t = 0.1,λ= 1,u(x,0)=1-x2 时（2. 5 ）解的图像；b. （右）t= 0.1,λ =1,u( x, 0) =g 3(x)时 （2. 5 ）解的图像。

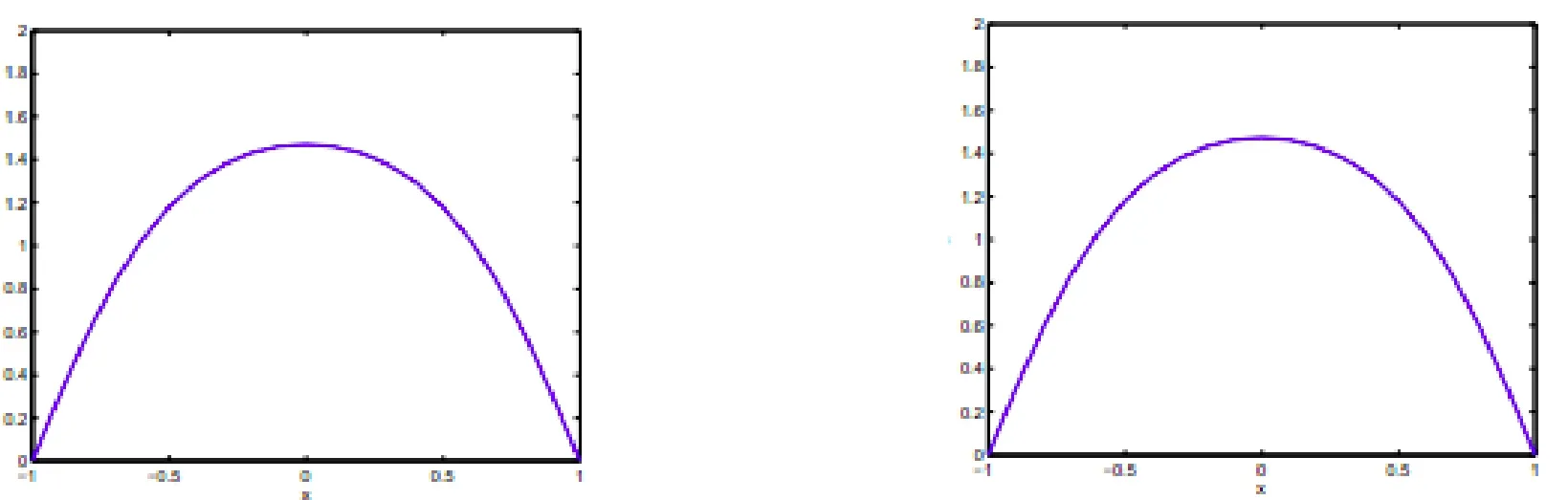
图4a.（左） t = 15, λ= 1,u(x,0)=1-x 2 时 （2. 5 ）解的图像；b. （右）t= 15,λ =1,u( x, 0) =g 3(x)时 （2. 5 ）解的图像。

综上，问题（2. 5 ）的解最终趋向某一个稳定的形式，实际上它应该是（2. 5 ）的平衡解，满足

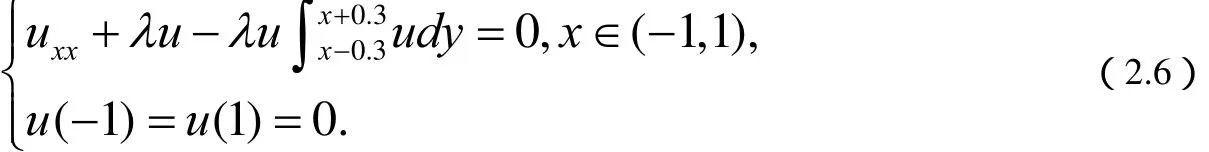
其中λ=10.对于更大的λ.通过实验得到的结果是一样的，只不过平衡解的图像有所差异，如图（图5（a）和（图5b）。解的图像。

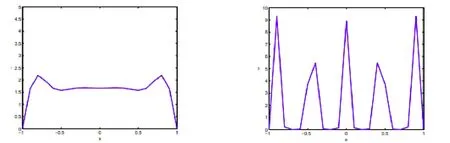
图5a.（左）t = 15, λ= 200,u(x,0)=1-x 2 时 （2. 5 ）解的图像:b.（右） t=15,

2.2 主要结果

我们通过上述数值模拟及与局部反应扩散方程的比较，可归纳总结如下实验结果，

1.若 λ＜ π2/4,(1.4)有一个稳定的平衡解u=0；

2.若 λ＞ π2/4,(1.4)有两个稳定的平衡解u=0和 u =uλ＞0.；

事实上，我们可以对任意维空间上的非局部问题（1.3）按上述方法进行数值模拟，得到相应数值结果1.若 λ＜nπ2/4，（1.3）有一个稳定的平衡解u=0；

2.若 λ＞nπ2/4，（1.3）有两个稳定的平衡解u=0和 u = uλ＞0；

其中 n=1,2,….

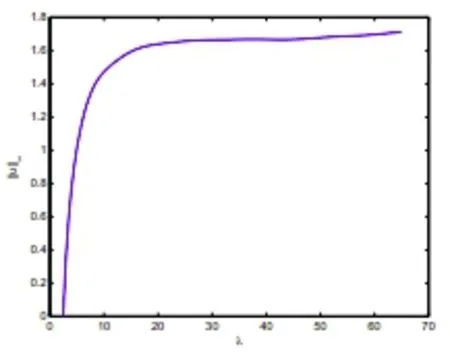
图6（2.5）平衡解的分歧图

本文我们只通过数值模拟观察并推断出（1.3 ）的平衡解得性态，我们将在其他文章中给出精确的理论的证明。

[1]A.L.Lin,B.Mann,G.Torres,B.Lincoln,J.Kas,and H.L.Swinney,Localization and Extinction of Bacterial Populations under Inhomogeneous Growth Conditions[J].Bio phys J.,87(2004),no.1,75-80.

[2]J.Wakita,K.Komatsu,A.Nakahara,T.Matsuyama,and M.Matsushita,Experimental Investigation on the Validity of Population Dynamics Approach to Bacterial Colony Formation[J].J.Phys.Soc.Jpn.63(1994),1205-1211.

[3]E.Ben-Jacob,I.Cohen,and H.Levine,Cooperative self-organization of microorganisms[J]. Adv.Phys,49(2000),395-554.

[4]V.M.Kenkre,Results from variants of the Fisher equation in the study of epidemics and bacteria[J].Proc.of.Amer.Phys.Soc.342(2004),242-248.

[5]M.A.Fuentes,M.N.Kuperman,V.M.Kenkre,Nonlocal Interaction Effects on Pattern Formation in Population Dynamics[J].Phys.Rev.Lett.91(2003),no.15,158104/1-4.

[6]孙丽男,王玉文,史峻平.非局部逻辑方程的数值分析[J].哈尔滨师范大学自然科学学报,2008,(2):27-30.

[7]陆金甫,关治.偏微分方程数值解法[M].北京:清华大学出版社,2005:82-84.

O29

A

1673-2219（2012）08-0001-06

2012－06－06

黑龙江省教育厅科学技术研究项目资助（项目编号11551308）。

李珊（1965－），女，江苏人，黑河学院数学系主任，教授，主要从事偏微分方程和数理统计研究。孙丽男（1983－），女，黑龙江人，黑河学院数学系讲师，硕士，主要从事偏微分方程研究。

（责任编校：京华，俊华）