基于粒子群优化的双力偶模型振幅谱反演方法及应用

郑建常 陈运泰

1）中国北京100081中国地震局地球物理研究所

2）中国济南250014山东省地震局

基于粒子群优化的双力偶模型振幅谱反演方法及应用

郑建常1，2），陈运泰1）

1）中国北京100081中国地震局地球物理研究所

2）中国济南250014山东省地震局

发展了一种基于全波形振幅谱的频率域双力偶震源机制反演方法.通过理论振幅谱与观测振幅谱的拟合搜寻断层面参数，基于粒子群优化算法可以在较短的时间内得到稳定可靠的解.数值试验表明，在定位误差较大，以及台站布局较差的情况下，振幅谱反演仍可较为准确地得到震源机制，并且由此计算得到的最优震源深度仍比较接近真实的震源位置.使用该方法用2010年5月17日渤海ML4.0地震的震源机制进行了检验，结果与加权P波初动解非常一致.应用该方法对山东半岛及近海地区2003—2010年14次ML≥4.0地震震源机制进行了估计.

矩张量 频率域 震源机制 粒子群优化 振幅谱 全波

引言

地震震源机制的测定是地震学的一项基本工作，它有助于了解震源区和区域性构造应力状态以及断层的构造特性，是理解地震孕育过程的重要途径.传统的求解震源机制的方法包括初动符号法、振幅比法等.对于中、小地震，在数据量较少以及台站布局等不理想的情况下，这些方法的应用都受到一定的限制（吴大铭等，1989）.区域性地震的波形记录包含了有关震源和区域地壳的丰富的信息，因此，在对地壳结构已知的情况下，可以利用矩张量反演的方法来求解这些地震的震源机制（Dreger，Helmberger，1993；Šíleny｀，Pseneik，1995）.

矩张量的波形反演既可以在时间域内进行，也可以在频率域内执行.对较大的远震，矩张量的频率域反演方法已经有了长足的发展（Mendiguren，1977；Kanamori，Given，1981，1982；Romanowicz，1982；Beck，Patton，1991；Cotton，Campillo，1995；Dufumier，Trampert，1997；Sasatani，1997；周荣茂，陈运泰，1999；Hernandezetal，1999；Nakanoetal，2008；Cescaetal，2010）.但是对于区域性的中小地震，由于其优势频率较高，易受到噪声和地壳结构误差及横向不均匀性的影响（Fordetal，2010），因此区域地震的矩张量反演比较复杂（郑建常，陈运泰，2012）.由于时间域反演需要对每个台站进行震相校正，人工对齐波形的到时，相对而言，波形的振幅谱对震相的平移不敏感，因此在频率域内利用振幅谱的反演方法在研究区域性地震时更具优势（卞爱飞等，2010）.

Patton和Zandt（1991）首先对用于远震的面波反演算法进行修改使之适用于区域性地震，并对内华达州1988年的一次核爆事件进行了研究；吴忠良和陈运泰（1994）使用直达P波、直达S波和SP转换波的位移地震图在频率域内对1985年4月18日云南禄劝MS6.1地震的15次余震在简单介质模型下进行了近震源记录的矩张量反演，结果显示对ML4.0—5.0的地震可以较好地给出震源机制解.Thio和Kanamori（1995）在利用区域相速度模型对观测数据进行震相校正，消除横向不均匀结构影响后，使用短周期面波（10—50s）谱反演了TERRA－scope台阵记录的超过180次的MW3.2—6.5南加州地方震事件的矩张量，结果与初动符号和其它波形反演方法得到的结果一致；Pasyanos等（1996）比较了区域面波反演与时间域矩张量反演方法的结果，并进行了中等地震矩张量解的准实时处理的尝试.Zahradník等（2001）发展了利用振幅谱与初动符号联合求解小震震源机制的方法，并应用该方法对希腊科林斯湾（Corinth Gulf）地区5次MW＜4的中小地震震源机制进行了研究；Cesca等（2006）提出了使用直达体波振幅谱在频率域反演偏量矩张量解的方法，使用合成数据对该方法进行了数值试验，在区域震中距范围内对西班牙地区中低震级的浅震震源机制的应用研究表明这一方法是稳定可靠的；许力生等（2007）应用频率域矩张量反演方法获得了首都圈地区2004年51次中小地震的矩张量解，并通过数值试验对反演结果进行了评价；Lashak等（2010）使用频率域矩张量反演方法，研究了伊朗地区9次中等强度的区域地震的震源机制.

近年来，随着数字化台网建设的加快，尤其是我国东部地区的地震台网密度有了很大的提高，可以求得更加可靠的小震震源机制解.但是由于受场地条件的限制，对于发生于海域的区域性地震，多数台站距离较远，无法得到清晰的初动；而一些近海和岛屿上的台站，虽然可以记录到波形，但台站的方位覆盖差，并且由于受到海浪和潮汐的影响，噪声干扰大，因此在使用振幅比或波形反演求解震源机制的方法时都受到了很大限制.鉴于这种情况，本研究致力于发展在频率域内使用理论振幅谱来拟合观测振幅谱的矩张量反演方法，以求解区域性中、小地震的震源机制.

1 理论与方法

1.1 基本理论

在点源和远场近似的情况下，地震在观测点r引起的位移可以表示为（许力生，陈运泰，2002）

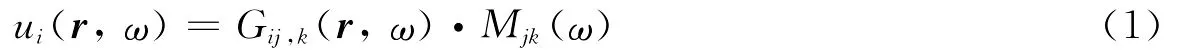
式中，ω为角频率，ui（r，ω）为地震的观测位移谱，Mjk（ω）为地震矩张量谱，Gij，k（r，ω）为格林函数（微商）谱.对于中小地震，由于震源破裂时间很短，可以用狄拉克δ－函数来表示震源时间函数（许力生等，2007）.这种情况下，式（1）可以写成

对于近区域中小地震，只考虑矩心周围的格林函数一阶项，位移谱ui（ω）可以表示为对应6种基本震源类型的基本地震图的谱Eij（ω）的加权和

系数aj与矩张量Mjk有关，在地理坐标系（x朝北为正，y朝东为正，z朝下为正）中，

由矩张量Mij的特征矢量可得断层机制的走向、倾角、滑动角；由特征值可得标量地震矩M0；在纯双力偶震源模型的约束条件下，矩张量的迹和行列式为零.

1.2 反演方法

在纯剪切位错的情况下，由于震源机制中没有体积分量，因此无需考虑各向同性分量的基本地震图，即公式（4）中a6＝0.其余5个权重系数ai可以表示为断层的走向φ、倾角δ和滑动角λ的函数.这5个系数与5种基本理论振幅褶积求和，由于格林函数谱是复数谱，对结果取模得到理论振幅谱.为了便于比较，反演时对理论和观测振幅谱进行归一化

式中，上下标s和k分别表示台站和震相.

本文使用基于一维速度模型的离散波数方法计算Green函数（Bouchon，1981）.使用L1范数来计算观测振幅谱与合成振幅谱之间的错配程度，错配函数定义如下：

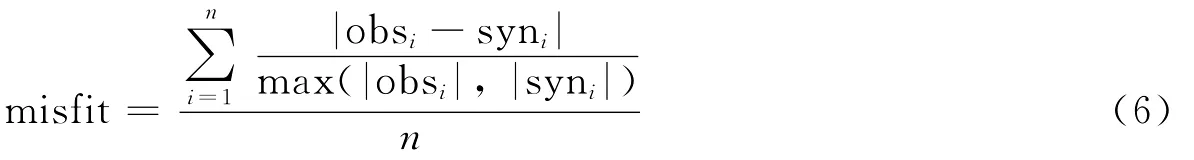
式中，obs表示观测振幅谱，syn表示合成振幅谱，n＝台站数×分向数×使用频率数.

对于约束为纯双力偶模型的矩张量，其震源机制的求解过程是典型的非线性最优化问题.传统的格点搜索会耗费大量的计算时间，且得到的解不是十分精确.因此在实际应用中，多采用不同的非线性优化算法（Sambridge，Drijkoningen，1992；Kobayashi，Nakanishi，1994；Zhouetal，1995；杨文采，2002；Šíleny｀，1998；Wuetal，2008；Godanoetal，2009）.我们使用了最近发展的粒子群算法来进行震源机制解的非线性优化搜索.

1.3 粒子群算法

粒子群算法（particle swarm optimization algorithm，简写为PSO）是近年来发展起来的一种新的全局优化算法（Kennedy，Eberhart，1995），属于进化算法（evolutionary algorithm）的一种.与遗传算法相似，粒子群算法也是从随机解出发，通过群体迭代寻找最优解，也是通过适应度来评价解的品质.但该算法比遗传算法规则简单，没有遗传算法的“交叉”和“变异”操作，而是通过粒子在解空间追随当前的最优粒子来寻找全局最优.该算法基于复杂适应系统（complex adaptive system，简写为CAS）理论，通过模拟生物群体迁徙、觅食、躲避猎食者的行为，离散的个体之间通过共享信息和集体协作使群体达到最优目的，是一种基于群体智能的优化方法.

粒子群算法相对于遗传算法和神经网络算法，具有一些优点.Hassan等（2005）以及Yang等（2008）通过一系列基准问题的测试，证明了与遗传算法相比，粒子群优化算法达到同样精度的解所需的计算用时更少，并且对于连续变量的非线性问题，粒子群优化算法的计算效率更高.

为了避免反演过程收敛到局部极小值，我们对粒子群算法进行了修改，采用断层的走向、倾角、滑动角的10°×10°×10°步长，对震源机制参数的解空间进行网格搜索得到的结果作为初始解，这样就保证了搜索过程可以稳定地收敛到全局最优解.数值试验表明，使用该算法进行搜索，反演过程可以较快地收敛到真实解（图1）.

2 数值试验

2.1 用于数值试验的数据与资料

为了检验方法的可行性，采用合成数据进行数值试验.用于数值试验的台站分布见图2.为了模拟实际地震的情况，假设台网给出的定位位置存在偏差，假设定位的震中相对真实的震中位置在经度和纬度上各偏移了0.05°，相当于偏离了约8km，这在近区域或者地方震的定位中属于偏离较大、精度较差的结果.用于检验的“真实”震源深度设为9km，标量地震矩M0＝1.0×1015N·m，矩震级MW4.0；震源机制设为走滑型，其断层面参数设为（该震源机制来自2010年10月24日周口太康MS4.6地震）：走向224°、倾角89°、滑动角－172°（图2）.同时，参考实际需要，为了模拟近海海域地震观测的实际情况，给出的台站分布的方位角张角范围不到90°，台站的震中距范围在100—300km之间.台站相对真实震源的震中距和方位角见表1.

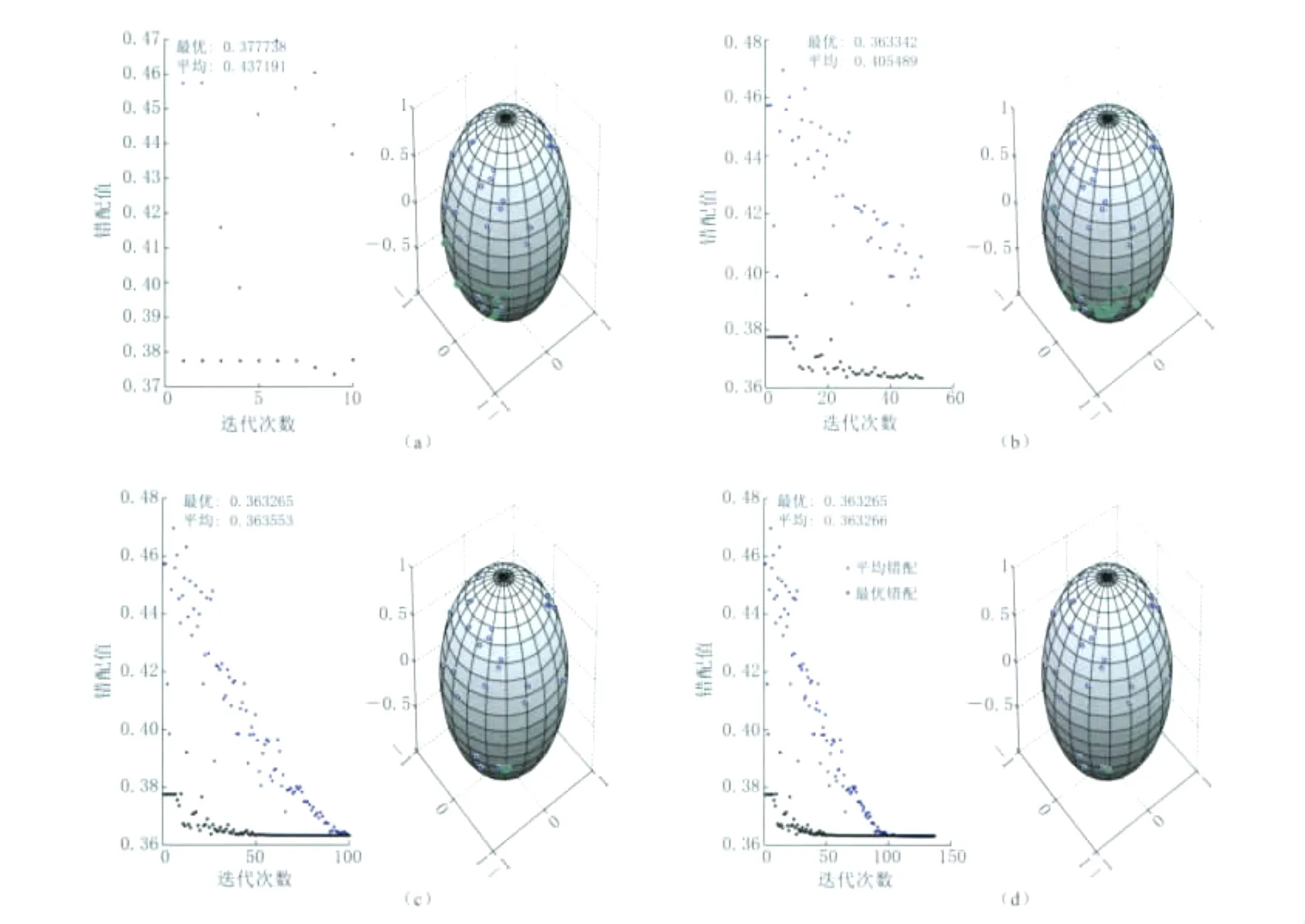
图1 粒子群算法搜索过程（a）迭代10次时解的分布；（b）迭代50次时解的分布；（c）迭代100次时解的分布；（d）迭代结束时解的分布.（a）—（d）图中左半部分为迭代中解的错配值变化，其中蓝色点为迭代中所有解的错配平均值，黑色点为这些解中的相对最优解；右半部分为解在震源球上的分布示意图，蓝色空心圆表示初始解的P轴在震源球上的投影；绿色实心圆为每一步迭代过程中解的P轴的投影Fig.1 Convergence of PSO algorithm’s searching procedure on focal sphere（a）Solution after 10iterations；（b）After 50iterations；（c）After 100iterations；（d）Iteration end.Left part of each panel shows misfit values for solutions in each iteration step.Blue points are mean misfit value for all solutions in each step，while black points are misfit value for relative optimized solution in each step.Right part of each panel denotes solution distribution on the focal sphere.Blue circles on the sphere denote Paxes of initial solutions，while green points are that of iterative solutions in each step

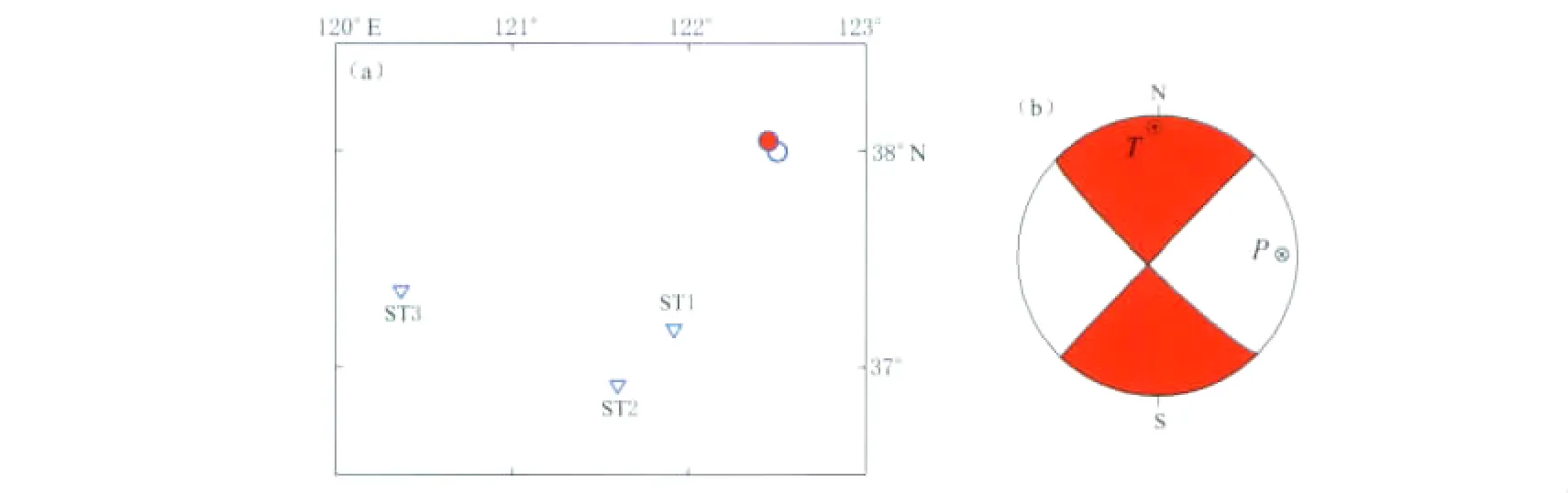
图2 用于数值试验的台站分布（a）及震源机制（b）（红色实心圆表示定位结果，蓝色空心圆表示实际震中）Fig.2 （a）shows earthquakes（circle）and stations（triangles），and（b）plots the focal mechanism used in numerical experiments.In（a）figure solid circle represents location result，blue circle represents true epicenter of test event

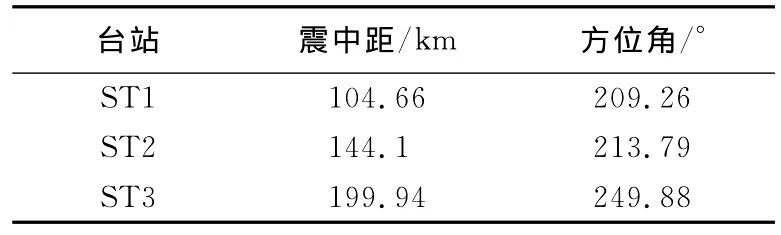
表1 用于数值试验的台站的震中距及方位角Table 1 Epicentral distance and azimuth of stations for numerical experiments

使用Bouchon（1981）的离散波数法，在0.01—1Hz频段内计算合成波形，作为用于数值检验的真实波形.图3给出了ST3台的添加了10%噪声的合成波形.

2.2 计算结果

在与真实震中位置存在偏离的定位位置上进行反演，使用如图3添加了10%水平均值为零的高斯白噪声信号的合成波形作为真实波形，像真实数据一样进行滤波.在深度方向进行搜索，起始深度为3km，搜索步长1km，最大深度20km，共18个深度位置.选用了0.10—0.20Hz的频段进行震源参数的反演，最终计算得到各个深度的最优解以及错配函数值见图4.反演得到的最佳深度h＝10km，与真实的深度h＝9km相差1km.在该深度位置上得到的标量地震矩为1.16×1015N·m，矩震级MW4.0，与真实值相差不大.反演得到的最佳震源机制与真实震源机制之间的差别不大，解的详细对比情况见表2.

表2 真实震源机制与反演结果的断层面参数的比较Table 2 Comparison between true solution and inversion result

由表2可见，反演得到的结果与真实解相差不大，得到的两个节面的走向的差异均在5°范围内，其中P轴方位的差异不到1°，T轴方位差在10°以内.

由真实解计算得到的观测振幅谱与对应搜索得到的最佳解的理论谱的对应关系见图5.值得说明的是，我们反演使用的频段为0.10—0.20Hz，分别在0.08—0.10Hz和0.20—0.208Hz频段使用了余弦边瓣.由图5可以看出，除了个别频率点外，大部分频率都符合得相当好.

对10km深度得到的最佳解计算合成波形，与真实解的合成波形进行比较，并计算了相关系数，结果见表3及图6.可以看出，大部分台站分向的波形拟合得相当好.

表3 最佳解合成波形与真实解合成波形的相关系数比较Table 3 Correlations between observed and synthetic waveforms

3 方法检验

3.1 数据与资料

据山东台网测定，北京时间2010年5月17日20时2分13.0秒，在渤海海峡（38.38°N，120.53°E）发生了ML4.0地震.

这次地震发生在庙岛群岛的西北侧，距离辽东半岛陆地超过100km，距离山东半岛最近不到70km.我们使用了来自于山东台网的波形数据，在震中距150km范围内主要有山东台网的6个台站（BHC，CHD，LOK，ZHY，YTA，LZH），主要分布在地震的南侧，以及辽宁台网用于数据交换的DL2和HSH两个台，位于地震的北侧.地震及台站分布见图7.

距离最近的BHC台存在问题，数据无法使用.根据台站波形的信噪比情况，选择了CHD，LOK，DL2，ZHY四个台站的数据用于反演.首先对台站的波形数据进行傅里叶变换，得到了观测谱.图8给出了CHD台（震中距55.22km）和DL2台（震中距111.86km）的垂直向波形的速度振幅谱和噪声谱.由图8可见，两个台均有较好的信噪比.

图9 本文使用的地壳速度结构模型Fig.9 Crustal velocity structure used in this paper

反演使用的速度模型是Park等（2006）给出的黄海地区中上地壳速度结构模型（图9）.该模型也是韩国地矿研究所（KIGAM，Korea Institute of Geology，Mining and Materials）使用的黄海至朝鲜半岛地区的地震定位速度模型.

由于矩张量反演对震中位置的较小误差不敏感，因此我们使用中国地震台网中心给出的全国小震目录中的定位结果，在深度方向进行搜寻.起始深度为3km，搜寻步长1km，最大深度20 km，共18个深度位置.

3.2 0.10—0.20Hz频段计算结果与分析

使用0.10—0.20Hz频段（周期5—10s）的振幅谱进行反演，图10给出了不同深度的最优解的错配值随深度的变化关系，以及最终得到的全局最优解.

反演得到此次地震的最佳深度在9km，该结果比台网中心给出的定位结果（12km）的震源深度要浅.由图10可以看出，我们使用的周期5—10s的波形对震源深度的分辨能力不是很好，尝试震源深度在8—13km之间时，解的错配值的差别不是很大.最佳震源机制解的错配函数misfit＝0.405 7.反演得到此次地震的标量地震矩约3.05×1014N·m，相当于矩震级MW3.7.

图10 0.10—0.20Hz频段反演得到的渤海ML4.0地震不同深度的最优解和错配值（a）以及全局最优解（b）Fig.10 Inversion results for Bohai Sea ML＝4.0event based on 0.10—0.20Hz data.（a）Optimized solutions at different focal depths；（b）Global optimized focal mechanism

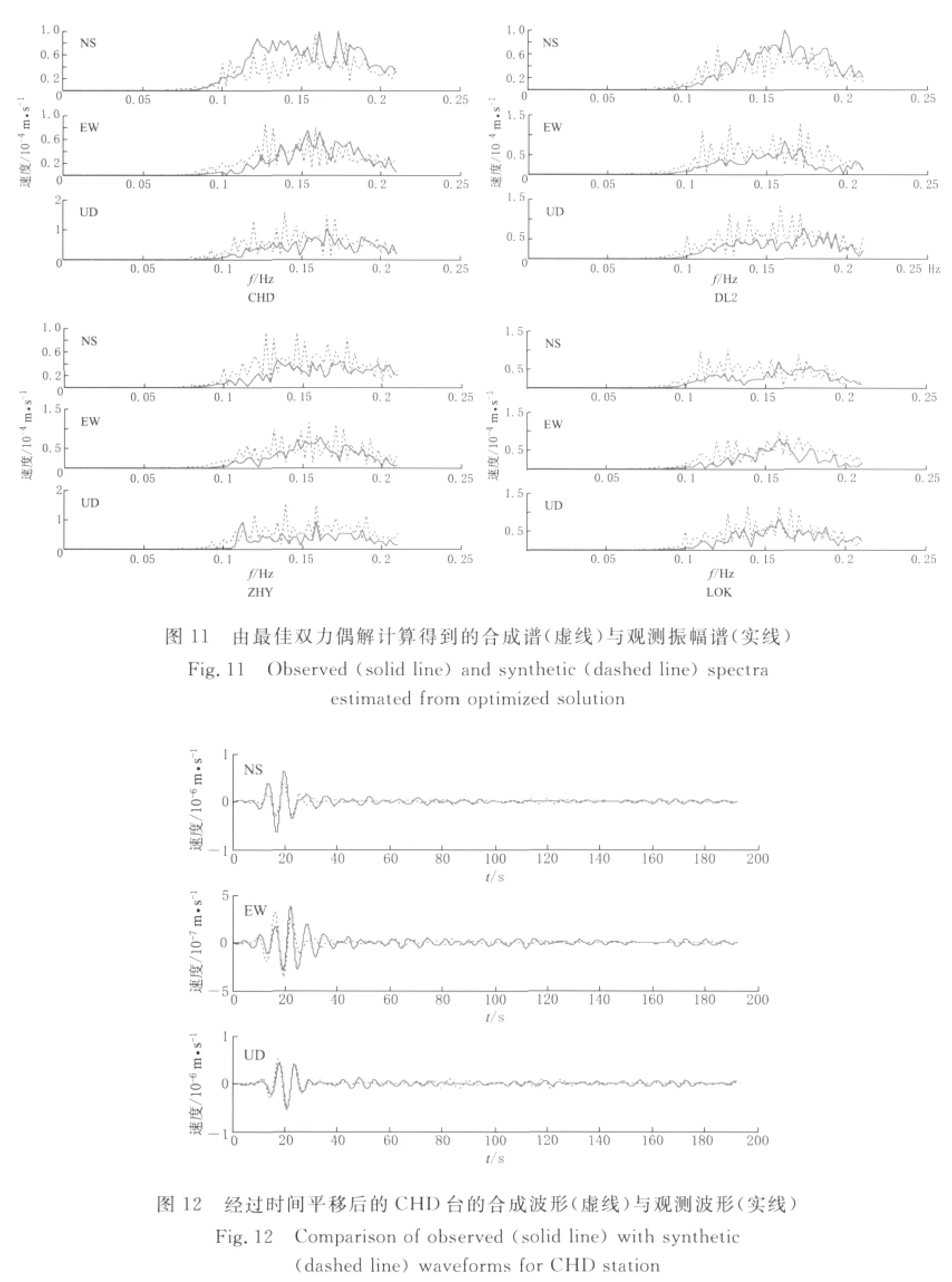
图11给出了最佳双力偶解计算得到的合成谱与观测振幅谱.使用反演得到的最佳震源机制解计算得到合成波形，图12给出了在对齐到时的情况下CHD台的波形拟合情况，3个分向的平均相关系数达到了0.757.由图可见，合成波形能够再现观测波形的基本震幅和主要特征，由理论谱得到的合成波形与实际的观测波形拟合的相当一致，这表明了方法的可靠性以及反演过程的准确性.

3.3 0.10—0.25Hz频段计算结果与分析

使用0.10—0.25Hz频段进行反演，得到了各个深度的最佳震源机制解以及相应的观测振幅谱与合成谱的错配值（图13）.由图13可见，最佳震源深度仍然为9km，与0.10—0.20Hz频段反演结果一致.在此深度上，最佳震源机制解对应的错配函数最小值为0.397，得到的标量地震矩为3.339×1014N·m，相当于矩震级MW3.7.与5—10s周期反演结果相比，最佳震源机制非常一致，标量地震矩也很接近.

由反演得到的最佳双力偶模型震源机制计算的合成波形与观测波形的平均相关系数约0.739（图略），稍低于0.10—0.20Hz频段的结果.由此可见，在反演过程中增加相对高频的成分，可以提高深度的分辨能力，但受一维速度结构模型的限制，有可能会减弱合成波形的拟合程度.

3.4 与初动符号解的比较

根据山东台网的波形资料，读取了17个台的初动符号，使用P波初动格点尝试法求解震源机制，得到的结果见表4.

与初动符号的震源机制相比，二者之间的最小空间旋转角（Kagan，1991）为11.24°，节面走向的差不到10°，P和T轴的方位位置均比较接近.进一步说明了方法的可靠性.

4 山东半岛及近海地区地震的反演结果

2003年以来，山东半岛两侧近海海域陆续发生了多次3—4级中小地震，受台站布局以及观测资料的限制，对这些地震一直没有开展过研究.我们采用上述的基于粒子群优化的双力偶约束的谱相关反演方法，对该区的地震震源机制进行了初步分析.为了保证反演质量，使用波形的相对低频部分，在合适的信噪比的情况下，我们共选择了该区2003—2010年ML≥4.0的14次地震用于计算.图14给出了这14次地震的震源机制解下半球投影的“海滩球”表示，表5中列出了这些地震的震源参数.

图13 0.10—0.25Hz频段反演得到的渤海ML4.0地震不同深度的最优解和错配值（a）以及全局最优解（b）Fig.13 Inversion results for Bohai Sea ML＝4.0event based on 0.10—0.25Hz data.（a）Optimized solutions at different focal depths；（b）Global optimized focal mechanism

表4 由P波初动符号得到的断层面解与振幅谱相关方法得到解的比较Table 4 Comparison of the fault plane solution obtained by polarity analysis with that of this paper

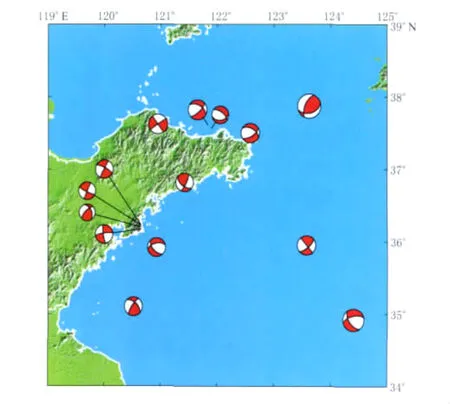
图14 研究区域的台站分布及本文得到的震源机制解Fig.14 Stations in studied area and focal mechanisms of earthquakes estimated by this paper

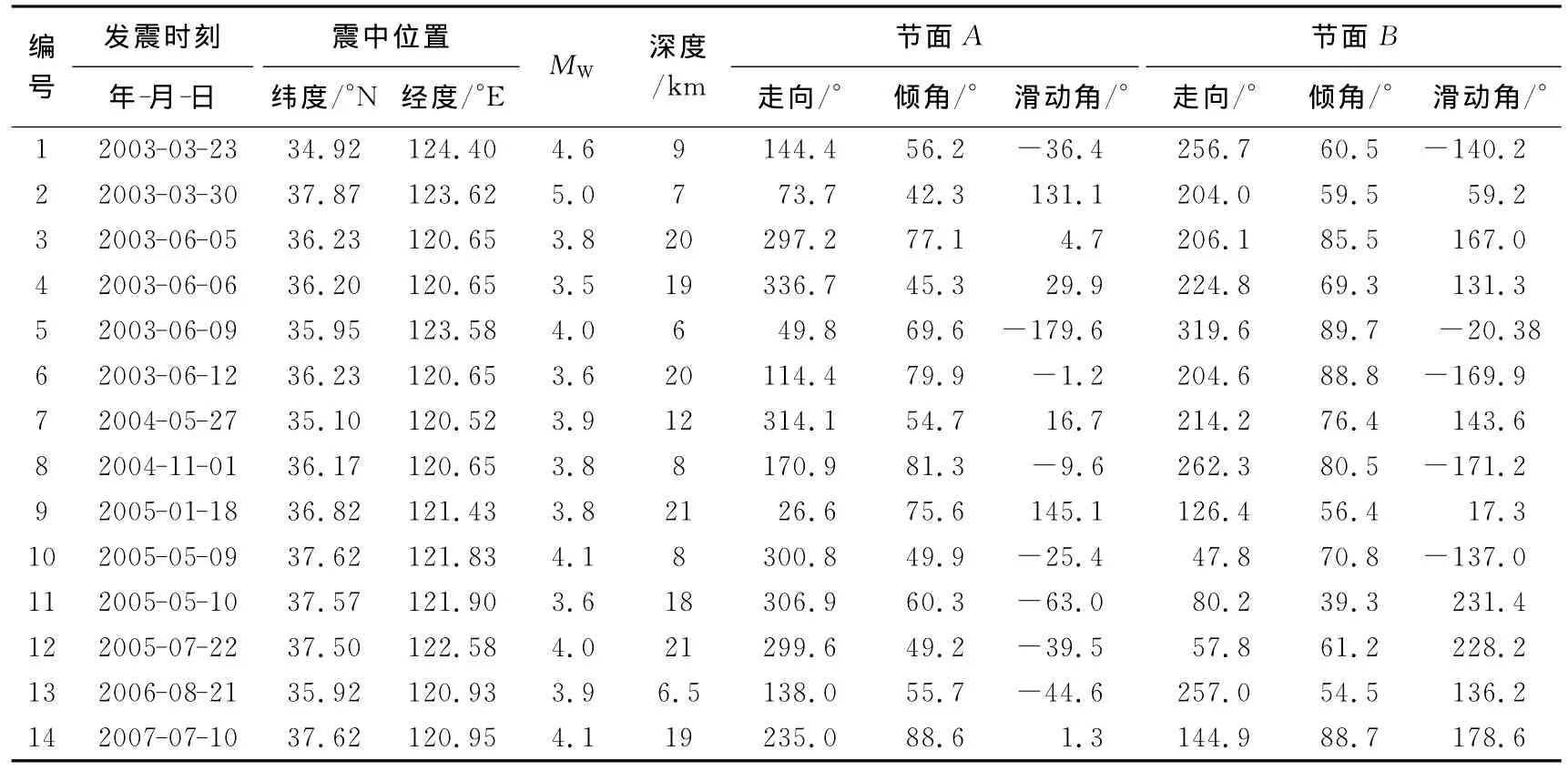
表5 本文得到的14次ML≥4.0地震的震源机制解参数Table 5 Focal mechanisms of 14earthquakes studied in this paper

5 讨论与结论

发展了一种基于全波形振幅谱的频率域双力偶震源反演方法.通过理论谱与观测谱振幅的拟合搜寻断层面参数，基于粒子群优化算法，可以在较短的时间内得到相对稳定可靠的解.

数值试验表明，在定位误差较大以及台站布局较差的情况下，通过振幅谱反演可以较为准确地得到震源机制，并且计算得到的最优震源深度接近真实的震源位置.

对于时间域波形反演，振幅谱方法速度更快，扣除仪器响应更容易，并且该方法既不需要确切的发震时刻，又无需对观测波形与合成波形进行人工对齐，减少了中间误差.此外，由于数据量少，观测谱与合成谱之间的拟合程度的量化也比波形要容易.因此更适合于区域中等地震的矩张量反演的自动化处理.

使用该方法对2010年5月17日渤海ML4.0地震的震源机制进行了检验计算.计算结果显示，此次地震的最佳深度为9km，标量地震矩M0＝3.049×1014N·m，相当于矩震级MW3.7；不同频段的反演结果相对稳定，震源机制结果与P波初动解的结果较为一致.

应用该方法对2003年以来山东半岛及其两侧近海海域发生的14次ML≥4.0地震的震源机制进行了研究，给出了最佳的双力偶震源机制解.反演得到的最佳深度与台网给出的地震目录的深度不尽一致.根据有关研究（许力生，陈运泰，1997），深度的误差对震源机制的结果影响不大.此外需要说明的是，受台站布局和早期数字化观测的数据质量较差的影响，对于距离陆地较远的海域地震，其结果的可靠程度相对较低.

感谢审稿专家为本文提出的修改意见和建议.本文使用的粒子群优化算法程序为S Chen（2010）给出的基于 Matlab的源代码（http：∥www.mathworks.com/matlabcentral/fileexchange/25986－another－particle－swarm－toolbox），并进行了部分修改，在此谨致谢忱.

卞爱飞，於文辉，周华伟.2010.频率域全波形反演方法研究进展［J］.地球物理学进展，25（3）：982－－993.

吴大铭，王培德，陈运泰.1989.用SH波和P波振幅比确定震源机制解［J］.地震学报，11（3）：275－－281.

吴忠良，陈运泰.1994.近震源宽频带记录的地震矩张量反演［J］.地震学报，16（2）：141－－152.

许力生，陈运泰.1997.震源深度误差对矩张量反演的影响［J］.地震学报，19（5）：462－－470.

许力生，陈运泰.2002.震源时间函数与震源破裂过程［J］.地震地磁观测与研究，23（6）：1－－8.

许力生，蒋长胜，陈运泰，李春来，张天中.2007.2004年首都圈地区中小地震的矩张量反演［J］.地震学报，29（3）：229－－239.

杨文采.2002.非线性地球物理反演方法：回顾与展望［J］.地球物理学进展，27（2）：255－－261.

郑建常，陈运泰.2012.稀疏台网反演区域地震偏量矩张量解的稳定性［J］.地震学报，34（1）：31－－43.

周荣茂，陈运泰.1999.由矩张量反演得到的北部湾地震的震源机制［J］.地震学报，21（6）：561－－569.

Beck L S，Patton H J.1991.Inversion of regional surface wave spectra for source parameters of aftershock from the Loma－Prieta earthquake［J］.BullSeismSocAmer，81（5）：1726－－1736.

Bouchon M.1981.A simple method to calculate Green’s functions for elastic layered media［J］.BullSeismSocAmer，71（4）：959－－971.

Cesca S，Buforn E，Dahm T.2006.Amplitude spectra moment tensor inversion of shallow earthquakes in Spain［J］.GeophysJInt，166（2）：839－－854.

Cesca S，Heimann S，Dahm T.2010.Rapid directivity detection by azimuthal amplitude spectra inversion［J］.JSeismol，15（1）：147－－164.

Cotton F，Campillo M.1995.Frequency domain inversion of strong motions：Application to the 1992Landers earthquake［J］.JGeophysRes，100（B3）：3961－－3975.

Dreger D S，Helmberger D V.1993.Determination of source parameters at regional distances with three－component sparse network data［J］.JGeophysRes，98（B5）：8107－－8125.

Dufumier H，Trampert J.1997.Contribution of seismic tomography in moment－tensor inversions using teleseismic surface－wave spectra［J］.BullSeismSocAmer，87（1）：114－－122.

Ford S R，Dreger D S，Walter W R.2010.Network sensitivity solutions for regional moment tensor inversions［J］.Bull SeismSocAmer，100（5A）：1962－－1970.

Godano M，Regnier M，Deschamps A，Bardainne T，Gaucher E.2009.Focal mechanisms from sparse observations by nonlinear inversion of amplitude：Method and tests on synthetic and real data［J］.BullSeismSocAmer，99（4）：2243－－2264.

Hassan R，Cohanim B，de Weck O.2005.A comparison of particle swarm optimization and the generic algorithm［C］∥Proceedingsofthe46thAIAA/ASME/ASCE/AHS/ASCStructures，StructuralDynamicsandMaterialsConference.Austin，Texas：AIAA：1－－13.

Hernandez B，Cotton F，Campillo M.1999.Contribution of radar interferometry to a two－step inversion of the kinematic process of the 1992Landers earthquake［J］.JGeophysRes，104（B6）：13083－－13099.

Kagan Y Y.1991.3－D rotation of double－couple earthquake sources［J］.GeophysJInt，106（3）：709－－716.

Kanamori H，Given J W.1981.Use of long－period surface waves for rapid determination of earthquake source parameters［J］.PhysEarthPlanetInteri，27（1）：8－－31.

Kanamori H，Given J W.1982.Use of long－period surface waves for rapid determination of earthquake source parameters 2：Preliminary determination of source mechanisms of large earthquakes（MS≥6.5）in 1980［J］.PhysEarthPlanet Interi，30（2－－3）：260－－268.

Kennedy J，Eberhart R.1995.Particle swarm optimization［C］∥ProceedingsoftheIEEEInternationalConferenceon NeuralNetworks.Perth，Australia：IEEE：1942－－1945.

Kobayashi R，Nakanishi I.1994.Application of genetic algorithms to focal mechanism determination［J］.GeophysRes Lett，21（8）：729－－732.

Lashak A B，Zare M，Mortezanejad G，Bayranvand S P.2010.Moment tensor inversion of nine events in Iran using INSN data［J］.JSeismol，14（4）：751－－760.

Mendiguren J.1977.Inversion of surface wave data in source mechanism studies［J］.GeophysResLett，82（5）：889－－894.Nakano M，Kumagai H，Inoue H.2008.Waveform inversion in the frequency domain for the simultaneous determination of earthquake source mechanism and moment function［J］.GeophysJInt，173（3）：1000－－1011.

Pasyanos M E，Dreger D S，Romanowicz B.1996.Toward real－time estimation of regional moment tensors［J］.Bull SeismSocAmer，86（5）：1255－－1269.

Patton H J，Zandt G.1991.Seismic moment tensors of western U S earthquakes and implication for the tectonic stress field［J］.JGeophysRes，96（B11）：18245－－18259.

Romanowicz B A.1982.Moment tensor inversion of long period Rayleigh waves：A new approach［J］.JGeophysRes，87（B7）：5395－－5407.

Sambridge M，Drijkoningen G.1992.Genertic algorithms in seismic waveform inversion［J］.GeophysJInt，109（2）：323－－342.

Sasatani T.1997.Source characteristics of the 1994Hokkaido Toho－Oki earthquake deduced from wide band strong motion records［J］.JourFacSciHokkaidoUniv，SerVII（Geophysics），10（2）：269－－293.

Šíleny｀J，Pseneik I.1995.Mechanisms of local earthquakes in 3－D inhomogeneous media determined by waveform inversion［J］.GeophysJInt，121（2）：459－－474.

Šíleny｀J.1998.Earthquake source parameters and their confidence regions by agenetic algorithm with a‘memory’［J］.GeophysJInt，134（1）：228－－242.

Thio H K，Kanamori H.1995.Moment tensor inversions for local earthquakes using surface waves recorded at TERRA－scope［J］.BullSeismSocAmer，85（4）：1021－－1038.

Wu Y M，Zhao L，Chang C H，Hsu Y J.2008.Focal mechanism determination in Taiwan by genetic algorithm［J］.Bull SeismSocAmer，98（2）：651－－661.

Yang F，Zhang C，Sun T.2008.Comparison of particle swarm optimization and genetic algorithm for HMM training［C］∥19thInternationalConferenceonPatternRecognition.New York：IEEE，2008：1－－4.

Zahradník J，Jansky J，Paptsimpa K.2001.Focal mechanism of weak earthquakes from amplitude spectra and polarities［J］.PureApplGeophys，158（4）：647－－665.

Zhou R，Tajima F，Stoffa P L.1995.Earthquake source parameter determination using genetic algorithms［J］.Geophys ResLett，22（4）：517－－520.

Amplitude spectrum inversion for double－couple source model with particle swarm optimization algorithm

Zheng Jianchang1，2），Chen Yun－tai1）

1）InstituteofGeophysics，ChinaEarthquakeAdministration，Beijing100081，China
2）EarthquakeAdministrationofShandongProvince，Jinan250014，China

An inversion method is proposed to best fit the observation in frequency domain with synthetic amplitude spectra of full waveform in seismic source mechanism studies.Grid search is performed for finding fault parameters by correlating theoretical spectra with observations.Employing particle swarm optimization algorithm，stable and reliable solutions can be obtained in shorter time.Numerical test shows that，in the case of large location error and worse station coverage，the inversion can result in the solutions close to the given true focal mechanism，and the focal depth near the real focus.The method has been applied to processing local and regional recordings of the 17May 2010ML4.0 earthquake in Bohai Sea region.The result is in agreement with that obtained from P wave polarity analysis.We also estimated focal mechanism solutions of 14ML≥4.0earthquakes in Shandong peninsula and its adjacent sea area from 2003to 2010.

moment tensor；frequency domain；focal mechanism；particle swarm optimization；amplitude spectrum；full waveform

10.3969/j.issn.0253－3782.2012.03.003

P315.3＋3

A

郑建常，陈运泰.2012.基于粒子群优化的双力偶模型振幅谱反演方法及应用.地震学报，34（3）：308－－322.

Zheng Jianchang，Chen Yun－tai.2012.Amplitude spectrum inversion for double－couple source model with particle swarm optimization algorithm.ActaSeismologicaSinica，34（3）：308－－322.

地震科技星火计划项目（XH12028Y）、山东省科技发展计划项目（2008GG10008004）与中国地震局监测预报司震情跟踪定向工作任务项目（2010020102）及山东省地震局博士基金联合资助.

2011－05－02收到初稿，2011－08－16决定采用修改稿.

e－mail：zjcmail＠yeah.net