改进粒子群算法及其在电力变压器优化设计中的应用

杜 江 李长波

河北工业大学电气工程学院 天津 300130

0 引言

电力变压器的优化设计问题是典型的工程优化问题，即在选用的优化算法稳定、可靠、寻优方便的基础上，在众多方案中寻求最优方案，使其既能满足工程问题中的约束条件，又可使优化设计问题的目标性能或指标达到最优［1］。优化设计方法广泛应用于化学工程和结构优化设计等问题当中，由于科技水平的不断发展和进步，需要解决的工程和技术问题变得更加复杂化、大型化和精密化，而优化设计方法正是解决这些问题的有效手段之一，因此，对优化算法的研究将会得到更加深入的发展。

近年来，随着信息科学与生命科学的快速发展，专家学者们将生物学中的遗传进化、群集智能等思想同计算机技术相结合，提出了许多新的算法。如遗传算法、人工神经网络算法、粒子群算法和蚁群算法等，这些算法统称智能优化算法。

粒子群优化算法（Particle Swarm Optimization,简称PSO算法）是由James Kennedy和Russell Eberhart通过对鸟群捕食行为的模拟所提出的，该算法适合解决多变量，多约束条件，非线性规划的工程问题，具有容易理解，易于实现，收敛速度较快等优点［2－3］。 但是，粒子群算法在处理维度较高的复杂问题时，容易出现早熟收敛的问题，即粒子群过早的聚集到局部最优解的邻域范围。

本文提出了一种带有速度惩罚量的改进粒子群算法，克服上述缺陷，实现算法在寻优精度和收敛性能上的提高。

1 粒子群优化算法

1.1 基本粒子群优化算法

粒子群算法的数学描述如下：

由m个粒子组成的粒子群体在一个D维搜索区域内进行寻优，其中每个粒子都包含两种信息：速度向量和位置向量。第i个粒子的位置向量为Xi=［Xil，Xi2，Xi3…XiD］， 速度向量为Vi＝［Vi1，Vi2，Vi3…ViD］，到目前为止粒子本身搜索到的最优位置为，粒子群当中所有粒子到目前为止搜索到的最优位置为Pi＝［Pi1，Pi2，Pi3…PiD］。 每次迭代粒子按照下式更新自己的速度和位置：

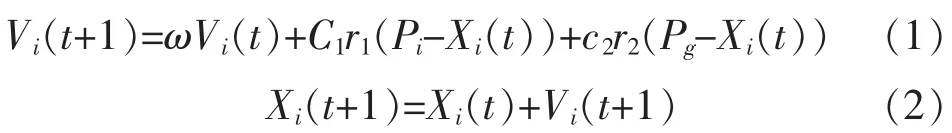
其中D为粒子的维度，每一维均为优化问题的一个变量；i=1，2，3， …，m表示粒子群当中的第i个粒子；t为粒子群迭代次数；c1、c2为粒子的学习因子或称为加速系数， 通常取c1＝c2=2；r1，r2为介于0和1之间的随机数；ω为惯性权重，控制之前速度对当前速度的影响［4－5］。

1.2 粒子群优化算法的改进策略

从粒子群速度迭代公式可知：在迭代后期，随着粒子群中的粒子逐渐向最优解的位置靠拢，粒子之间的差异性减小，粒子的迭代速度也减小，对于维度较大的复杂问题，往往存在多个极值点，粒子群很有可能陷入局部最优解的邻域内无法跳出，找不到全局最优解。

因此，本文提出了一种带有惩罚量的改进粒子群算法（particle swarm optimization with punishment factor简称PPSO算法）。其基本思想是在粒子群迭代过程中，通过判断粒子的聚集程度，对粒子群的聚集行为进行惩罚：若聚集程度明显，则增加粒子的飞行速度，使其能够跳出局部最优解的邻域。粒子的聚集程度可用粒子的适应度方差s2来表示，即

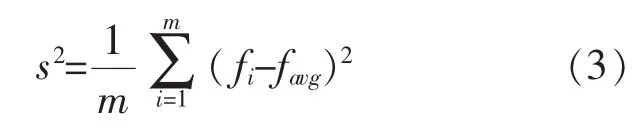
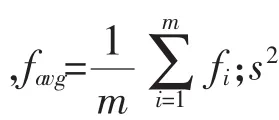
带有惩罚量的粒子群算法速度迭代公式为：

其中：α为惩罚量；μ为惩罚系数，与粒子的运动范围和飞行速度有关。

带惩罚量的改进粒子群优化算法的实现过程如图1所示。

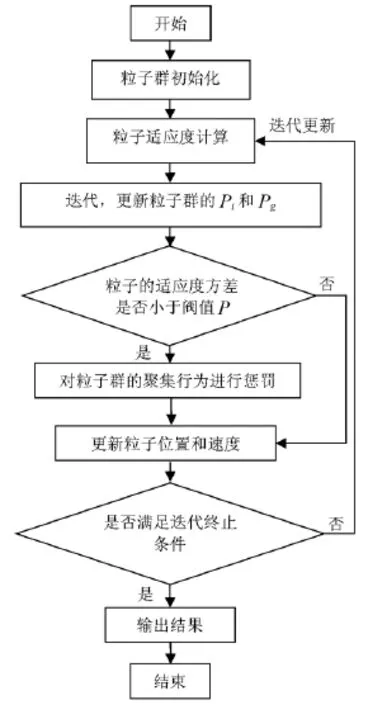
图1 改进粒子群优化算法流程图

1.3 算法测试

为了测试算法的寻优能力，将标准测试函数对基本粒子群算法和改进之后的粒子群算法进行仿真实验。本文选取Rosenbrock和Bastrigri作为测试函数，两函数优化难度大，所以常用来进行算法性能的测试。

Rosenbrock函数为：

Bastrigri函数为：

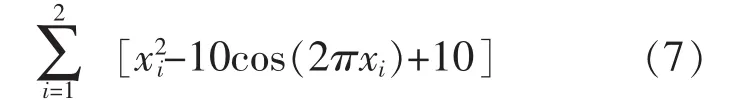
两函数的实验参数如表1所示。

两种粒子群算法中参数选取为：粒子种群规模为10；粒子维度为2；惯性权重ω值随算法迭代由0.9线性递减至0.4；学习因子c1，c2取为2；惩罚阀值p取为0.001；惩罚系数μ取为2；

分别对两种算法进行50次试验，测试结果如表2，3所示：其中表2为给定迭代次数N＝200时，两种算法得到的平均精度和适应度方差；表3为给定精度要求，两算法的平均迭代次数。

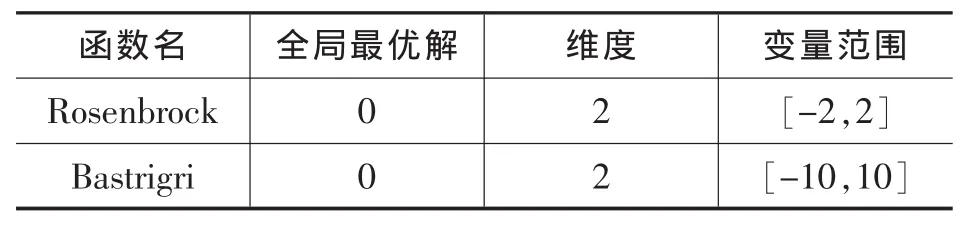
表1 测试函数及其实验参数

表2 算法的精度及适应度方差

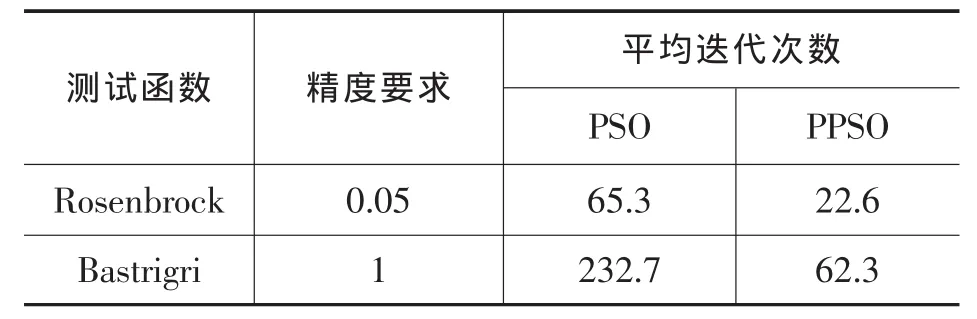
表3 算法的平均迭代次数

由表2、表3的数据可知：在迭代次数一定的情况下，改进的粒子群算法能得到更好的精度；达到一定精度要求，改进的粒子群算法所需迭代次数更少。

为了更直观的对算法的性能进行比较，给出了两函数的适应度值随迭代次数变化的曲线，如图2、3所示。

图2 Rosenbrock函数适应度曲线

由图2、3可见，改进的粒子群算法在算法精度和收敛性能上均有提高，较好的抑制了粒子群易陷入局部最优解的缺陷，提高了粒子群算法的寻优能力。

图3 Bastrigri函数适应度曲线

2 电力变压器的优化设计数学模型建立

优化设计问题通常的数学模型为

其中为优化问题中变量的集合；F（X）为优化问题的目标函数；Gi（X）为优化问题约束函数，即变量满足的约束条件。

2.1 优化设计目标函数的确定

针对变压器的设计问题，可以从多方面对其进行分析，建立不同的优化目标函数。考虑到变压器电磁设计过程主要是针对铁心和绕组部分进行设计，因此，本文从降低变压器的有效材料成本角度出发，建立以有效材料总成本最小为目标的目标函数，即

其中Pfe为硅钢片材料的单价；G（X）fe为所用硅钢片的总重量；Pcu为绕组导线材料单价；G（X）cu为所用绕组导线的重量。

2.2 优化变量的选取

在优化设计问题中合理正确的选取优化变量，可以简化优化问题的复杂性，提高优化算法的效率，取得更加合理的优化方案。针对变压器的优化设计问题特点，优化变量的选取原则为：变量的独立性较强；选取的变量应能明显影响变压器的关键技术参数，如有载损耗，阻抗电压；变量的选取应能确定变压器的设计参数等［6－7］。

基于以上原则，并考虑到粒子群优化算法更适合求解变量是连续变化的优化问题，因此，应用粒子群优化算法的变压器设计选取的优化变量为铁心直径选用系数KD，铁心磁密BC，低压线圈电流密度Cj2，高压线圈的电流密度Cj1等。

2.3 约束条件的选取

所设计变压器的负载损耗PS、空载损耗PO、短路阻抗UK、空载电流IO、高低压线圈对油面的温升等均应满足国家标准规定的范围，同时，变压器设计中的一些约束如铁心磁密、高低压线圈电流密度、扁导线的宽厚比等也应满足条件［8－9］。

2.4 带惩罚函数的变压器的优化设计目标函数的建立

由于粒子群算法所具有的非约束性，可考虑将带有多约束条件的优化设计问题转化为粒子群算法更易实现和应用的无约束条件限制的优化设计问题，同时，惩罚函数法是解决这类问题时最常用的方法，具有效率高，实现简单等优点，因此，本文采用惩罚函数法对风电场用电力变压器优化设计中的约束条件进行处理。惩罚函数法的基本思想是建立约束条件的惩罚函数，并将建立的惩罚函数同要求解的目标函数组合为一个新的、无约束条件的目标函数［10－11］。

带惩罚函数的变压器优化设计目标函数为：

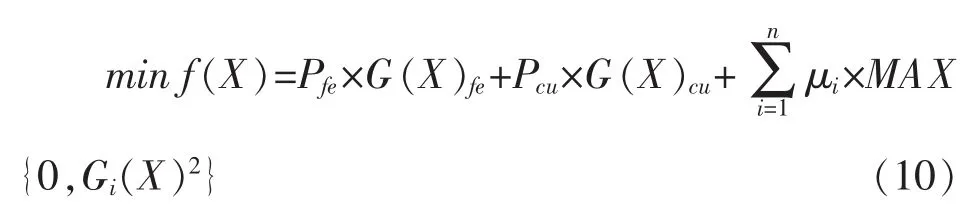
将此目标函数作为粒子群算法的适应度函数来进行迭代：如果优化变量不满足约束条件限定范围时，则会受到惩罚函数的惩罚，粒子的适应度较差，则粒子逃离惩罚区域，因此，随着迭代的进行，粒子在满足约束条件的解域中寻优。

3 电力变压器优化算例及数据分析

将改进的粒子群优化算法应用于风电场电力变压器SF9－630／10，其额定数据为：额定容量为SN＝630kVA；额定电压为高压侧线电压UL1=10500×（1±5%）V，低压侧线电压UL2＝690V；连接组号为Dyn－11；空载损耗PO＝1200W；空载电流IO＝1%；负载损耗PS＝6200W；短路阻抗UK＝6%；

改进粒子群算法的参数：粒子群种群规模S＝10；粒子的维度D＝4；惯性权重系数随迭代次数增加从0.9线性递减至0.4；学习因子c1=c2=2；迭代次数；惩罚阀值p=25；惩罚系数μ＝10。

常规设计方案与改进粒子群优化算法设计方案数据对比如下表4、表5所示。

由表6中数据可知，较之常规设计方案，应用改进粒子群优化算法的变压器的设计方案在有效材料成本上有了可观性的减少，但负载损耗、空载损耗、高低压线圈的温升等性能数据有了增加。

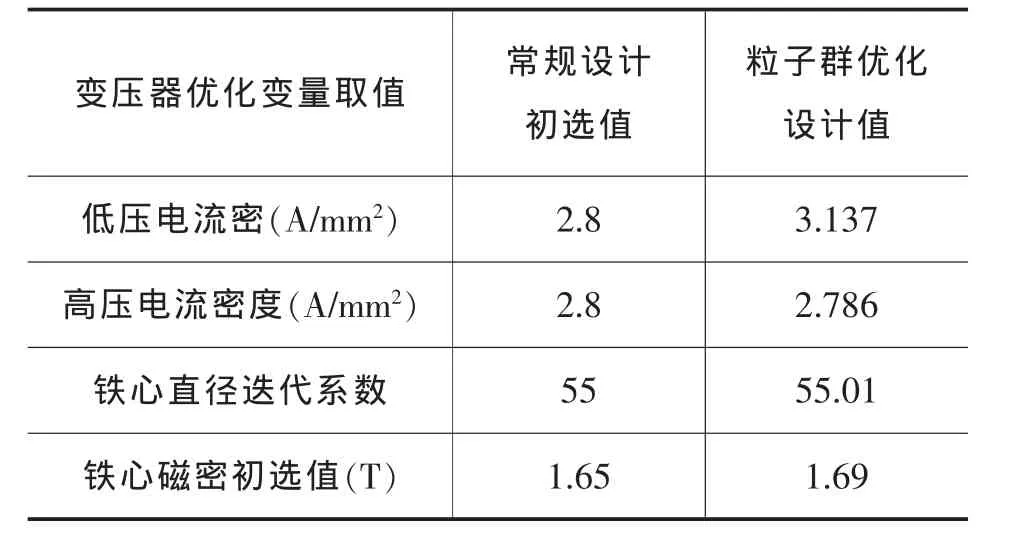
表4 变压器优化变量取值

表5 变压器设计中的关键设计量

实验数据表明：变压器设计当中有效材料使用量的减少必然引起变压器的负载损耗等性能参数的增加。因此，在设计变压器时应结合实际应用情况，综合考虑制造成本和损耗成本的影响，设计出较优的方案。

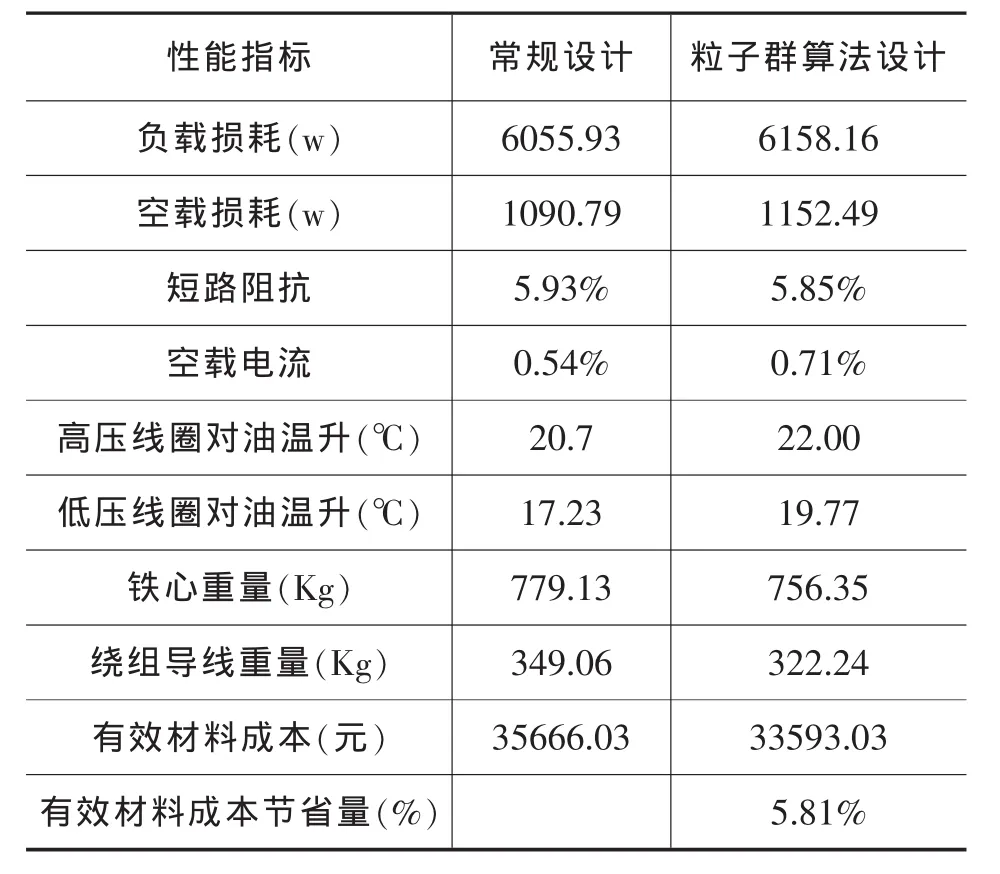
表6 变压器设计方案的性能参数值

4 结论

本文将带有速度惩罚量的粒子群算法应用于电力变压器的优化设计，通过对算法的测试和应用实例数据分析，可得出以下结论：改进的粒子群算法在算法精度和收敛性能上均有提高，较好的抑制了算法易陷入局部最优解的缺陷；应用改进粒子群算法的优化设计方案在满足变压器约束条件的基础上，变压器的有效材料成本较之常规设计方案有了可观性的减少，该算法用于变压器的优化设计问题是切实可行的。

［1］路长柏，朱英浩.电力变压器计算［M］.哈尔滨:黑龙江科学技术出版社，1986.

［2］于颖，李永生，於孝春.粒子群算法在工程优化设计中的应用［J］.机械工程学报， 2008，44（12）:226－229.

［3］J.Kennedy， R.Eberhart.Particle Swarm Optimization ［C］.In Proceedings of IEEE International conference on Neural Networks，1995，pp.1942－1948.

［4］R.Eberhart， Y.Shi， and J.Kennedy.Swarm Intelligence［M］.San Mateo， CA:Morgan Kaufmann， 2001.

［5］Angeline P J.Evolutionary Optimization Versus Particle Swarm Optimization:Philosophy and Performance Differences［J］.Evolutionary Programming，1998，256－260.

［6］姚志松，姚磊.中小型变压器使用手册［M］.北京：机械工业出版社，2008.

［7］邱清泉，励庆孚，钱虹凌，李涛.电力变压器优化设计系统构建［J］.电气应用，2006，25（4）:39－42.

［8］吴硕麟.电力变压器的数学模型和参数决定［J］.电工技术学报，1990，2:24－28.

［9］E.Schmidt，P.Hamberger.Design Optimization of Power Transformers［M］， 2004 International Conference on Power System Technology， 2004，1375－1380.

［10］张晶，翟鹏程，张本源.惩罚函数法在遗传算法处理约束问题中的应用［J］.武汉理工大学学报， 2002，24（2）:56－59.

［11］王蕾.非线性约束优化问题［J］.辽宁工学院学报，2003，23（1）:13－15.

［12］高隆昌，高增安.限制函数、惩罚函数及其性质初步［J］.西南民族大学学报（自然科学版）， 2003，29（5）:521－526.

［13］韩力，李辉，杨顺昌，何蓓.应用改进遗传算法的电力变压器优化设计 ［J］.重庆大学学报 （自然科学版），2002，25（9）:8－10.