改进电导增量法的光伏电池MPPT仿真

刘 萌 孙少华 杜之正 马晓勇

1.华北电力大学 自动化系 河北 保定 071003；

2.华北电力大学 电子与通信工程系 河北 保定 071003

0 引言

光伏阵列的输出功率随着光照强度、电池板温度和输出电压的不同而发生变化，但是在每一种工作环境下只有一个最大功率输出点，而且可以通过调节当前光伏阵列的输出电压来改变当前的输出功率，使系统工作在当前的最大功率点处，而其对应的电压则称为最大功率点电压。

电导增量法的思想是通过比较光伏阵列的瞬时电导和电导的变化量来实现系统的最大功率跟踪（MPPT）［2］。 该方法能够实现真正意义上的最大功率跟踪，但针对光照强度和环境温度快速变化时，很难同时满足系统的跟踪精度和速度［3］。本文针对传统的电导增量法动态性能和稳态性能不能同时兼顾的特点，提出了新型的变步长电导增量跟踪方法。仿真实验结果表明，当外界环境快速变化时，相对于传统的电导增量法，本方案能够兼顾系统的动态和稳态性能，提高系统的响应速度和减少系统的稳态震荡。

1 光伏电池的输出特性

1.1 光伏电池的等效电路模型

光伏电池的等效电路如图1所示。它相当于一个电流为Iph的恒流源与一只正向二极管并联。流过二极管的正向电流在光伏电池中成为暗电流Id。Rsh为旁路电阻，Rs为串联电阻。从电路原理可以推知单个光伏电池终端的电流关系［4］，如式（1）。

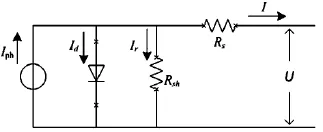
图1 光伏电池的等效电路

其中，

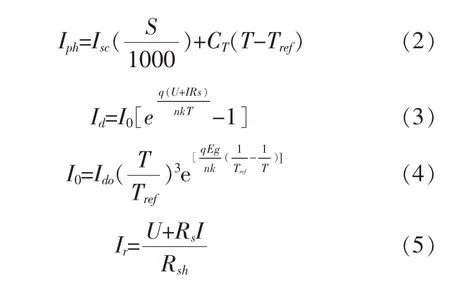
式中，T为电池板温度；q和k为电子电荷量及波尔兹曼常数，Tref为绝对温度。Eg为能带系能量，CT为温度系数，Rs为串联电阻，Rsh为并联电阻，n为二极管排放系数，Ido为二极管反向电流，Isc为短路电流；本篇论文参考的是天威英利能源有限公司生产的额定功率为50W的多晶硅光伏板的数据［5］。

1.2 光伏电池的输出特性

通过图1的电路模型，基于Matlab／Simulink软件实现的光伏电池模型的输出特性仿真，程序由M语言编写。

首先利用公式（2）和公式（4）计算出Iph和I0，使输出电压U为自变量，输出电流I为因变量，并赋初值为0。利用公式（1），电压U增加0.01V则计算当前电压下的电流，功率则为相应电压和电流的乘积。利用绘图程序就获得了不同温度和光照强度下光伏电池的功率电压曲线和电流电压曲线，分别如图2和图3所示。

图2 相同温度不同光照下电池的功率电压曲线

图2和图3中的各三条曲线分别是温度为300K以及光照强度分别为400W／m2、600 W／m2和800W／m2时获得的光伏电池功率电压曲线和电流电压曲线。其仿真结果跟太阳能电池输出特性的理论分析相吻合，很好的体现了实际系统中的光伏阵列输出特性，并且满足本文对仿真的要求。由图2可以看出，光伏电池有一个最大工作点，即最大功率点（MPP），它的值取决于光伏阵列的工作温度和外界光照强度。其随着温度和光照强度的不同而发生变换。

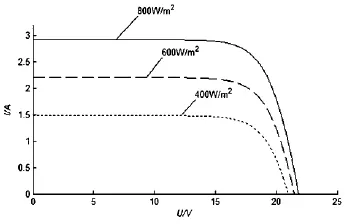
图3 相同温度不同光照下电池的电流电压曲线

2 最大功率点跟踪方法

2.1 传统的最大功率点跟踪方法

目前比较常用的光伏电池最大功率点跟踪方法有恒定电压法、干扰观测法和电导增量法［1］。

设最大功率点功率为Pm，对应的电压为最大功率点电压为Um。恒定电压法是在光伏阵列和负载之间通过一定的阻抗变换，使得系统成为了一个稳压器，即阵列的工作点总固定在Um附近。其优点就是系统具有良好的稳定性和可靠性，但是在早晨和中午温差比较大的地区，温度对光伏阵列的输出会产生较大的影响，采用恒电压法会使整个系统的效率降低［1］。

干扰观测法的原理是隔一定的时间改变系统的输出电压，观测之后的输出功率变化，来决定下一步的Ur（输出电压的变化量）的大小和方向。这种控制方法算法比较简单，且易于硬件实现，但是系统的响应速度较慢，只适用于光照强度变化缓和的情况。这种算法还可能会导致光伏阵列的实际工作点在其最大功率点附近振荡，造成功率损失；当光照快速变化时，跟踪算法有可能会失效，使系统判断错误的跟踪方向［8］。

电导增量法通过对比光伏阵列的电导增量和瞬时电导来改变控制Ur，Ur的绝对值称为步长A。光伏阵列P－U曲线表明最大值Pm处的功率斜率为零，所以有

式（7）即最大功率点的条件，当输出电导的变化量为输出电导的负值时，光伏阵列工作就在最大功率点处。电导增量法为真正意义上的最大功率跟踪，但是其算法受步长的制约，步长过大容易使系统发生稳态震荡，步长过小使系统很难快速的跟踪到最大功率电压处［9］。

2.2 基于参考开路电压的变步长电导增量法

由于系统当前的最大功率点的输出电压大约为系统当前光伏阵列开路电压Uc的0.8倍，以0.8Uc为起始电压进行跟踪。这样可以改善系统的响应速度，使其快速的跟踪到实际最大功率点电压附近。传统的电导增量法采用固定步长进行跟踪控制。当步长选择过大时，能够使系统快速跟踪当前最大输出功率，但无法满足稳态要求；当步长选择较小时，又导致跟踪速度过慢，动态性能降低。

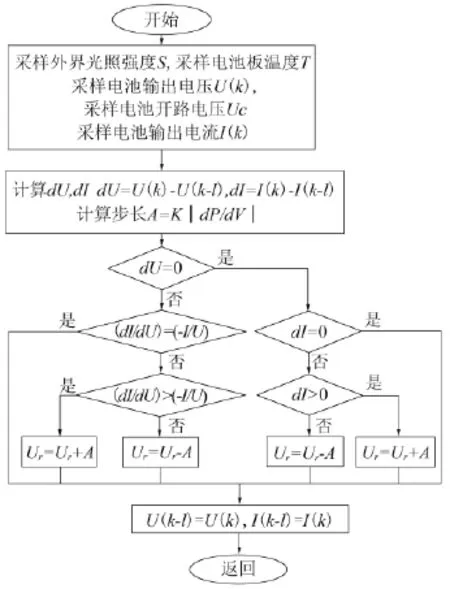
图4 变步长电导增量法的流程图

鉴于传统电导增量法的不足，在此采用变步长方式进行系统的跟踪，取步长为A＝K｜dP／dU｜，其中K为比例系数，dP为输出功率的变化量，dU为输出电压的变化量。当系统的外界环境快速变化时，先使系统的输出电压变化到0.8Uc处，然后再利用变步长电导增量法继续寻找系统的实际最大功率点。由公式（7）以及图2可以得知，当dP／dU＞0时，系统的工作电压小于最大功率点电压，需要增加当前输出电压；当dP／dU＜0时，系统的工作电压大于最大功率点电压，需要增大当前输出电压。其程序流程图如图4所示，系统的初始输出电压设定为其光伏电池开路电压的0.8倍。

3 最大功率点跟踪控制的仿真

3.1 传统增量法的仿真

在本次仿真中，设定在t＝0.1s时光伏电池的温度从298K突升到330K，t＝1.6s外界的光照强度从800W／m2突升为950W／m2。分别考察传统的固定步长电导增量法的跟踪曲线和变步长电导增量法的跟踪曲线。

图5、图6分别是取固定步长A＝0.05V和A＝0.1V时的跟踪仿真曲线。仿真结果分析得知，系统采用固定步长电导增量法控制，步长A＝0.05V时，系统较慢的跟踪到当前的最大输出功率，稳态震荡很小，系统具有良好的稳态性能；步长A＝0.1V时，系统能够快速的跟踪到当前的最大功率输出点处，但是在进入稳态后，系统发生了较为严重的震荡，从两个仿真曲线来看，如果固定步长的进行最大功率跟踪，很难选择合适的步长兼顾系统的动态和稳态性能进行跟踪。

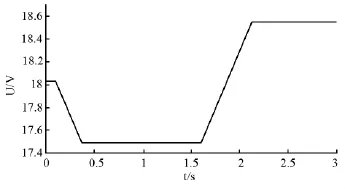
图5 步长为0.05V时的电池输出电压

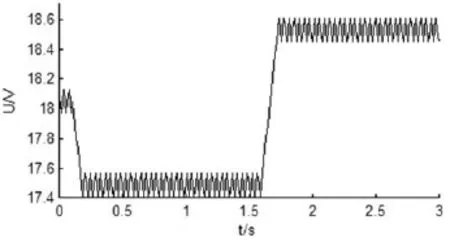
图6 步长为0.1V时的电池输出电压

3.2 变步长电导增量法的仿真

图7为采用变步长电导增量法的光伏电池输出电压波形。其外界环境同样设定为固定步长电导增量法的情况。

图7 变步长电导增量法的电池输出电压

从图7可以看出，系统的响应时间比图5的较快，可能快速的跟踪到当前的最大功率点处；而进入稳态后，系统的稳态性能较图6减少了系统的稳态震荡，能够使系统稳定的工作在当前的最大功率点处。

4 结论

针对传统固定步长电导增量法的缺点，并结合光伏电池最大功率点的特性，通过MATLAB软件M语言的编程进行了仿真实验。通过仿真实验可以看出，采用初始参考输出电压为当前光伏电池开路电压的0.8倍可以使系统直接在最大功率点附近寻找实际的最大功率点；采用变步长电导增量算法能保证光伏电池快速的跟踪到当前最大功率点处，并且在最大功率点处的震荡极小，稳态性能较好。仿真结果表明该方法的可行性。

［1］赵争鸣，刘建政，孙晓瑛，袁立强.太阳能光伏发电及其应用［M］.北京：科学出版社，2005.

［2］徐鹏威，刘飞，刘邦银.几种光伏系统MPPT方法的分析比较及改进［J］.电力电子技术，2007，（5）.

［3］司传涛，周林，张有玉，刘强，冯玉.光伏阵列输出特性与MPPT控制仿真研究［J］.华东电力，2010，38（2）：285－288.

［4］王丽萍，张建成.光伏电池最大公路点跟踪控制方法的对比研究及改进［J］.电网清洁能源，2011，27（2）：52－55.

［5］Texas Instruments Corp.Improved charging methods for Lead －Acid batteries using the UC3906.U －104，Texas，USA：TI Corp.1999.

［6］魏巍.光伏发电系统中最大功率点跟踪方法的研究［D］.西安：西安理工大学，2010.

［7］苏义鑫，向炉阳，张丹红.基于改进扰动法的光伏电池MPPT仿真研究 ［J］.武汉理工大学学报，2012，34（2）：135－139.

［8］周德佳，赵争鸣.具有改进最大功率跟踪算法的光伏并网控制系统及其实现［J］.中国电机工程学报，2008，28（31）：94－100.

［9］张弛，张代润.基于改进的变步长光伏并网系统MPPT控制策略研究［J］.电测与仪表，2012，49（1）：67－71.