在数控编程教学中的宏程序教学
2012-12-06陈曦
陈 曦
(重庆机械电子技师学院,重庆 400037)
在数控编程教学中的宏程序教学
陈 曦
(重庆机械电子技师学院,重庆 400037)
宏程序可以编制出一些由数学表达式给出的曲线轮廓,它将是数控加工技术的主要发展趋势。其最大的特点就是能比较轻松地编制非圆非直线曲线。宏程序的关键之处在于节点的选择和控制,宏程序的优点是遇到类似无法用普通插补描述的曲线时,把非常烦琐的普通编程演变成一种比较固定的简单的循环编程。宏程序的学习本身与实际使用结合得比较紧密,让学生明白所学即所用,能以用代学的道理。
宏程序;插补技术;直线(圆弧)逼近曲线法;节点的计算;变量自加
所谓宏程序在很多专业数控产品介绍中即为用户宏程序的简称,其功能是把一组采用变量和演算式的命令所构成的某一功能或者是动作集中存放在数控装置中,而记录这组命令的用户宏程序体就是宏程序。一般说来,类似于一般的直线插补命令如G01XZ,宏程序也可以用一个特定的指令代码来调用。在数控编程的时候由于普通数控指令只能进行直线和圆弧的插补功能(即G01、G02、G03),所以无法编制出像抛物线、椭圆等这样的一些由数学表达式给出的曲线轮廓,只能用直线和圆弧去逼近这些曲线。
随着数控技术与计算机辅助制造软件的迅速发展,在数控编程方面,单一的直线与圆弧插补命令已不再能满足各种型面的编程需要,越来越多的宏程序在数控编程加工中被应用。宏程序将是数控加工技术的主要发展趋势。
一、如何引入宏程序的学习
兴趣是学习的最好老师。首先应该考虑如何激发学生学习这门课程的兴趣。这些学生对手动编程加工已经比较熟练,一般的直线圆弧类工件的编程对于他们来讲已经不在话下,各种编程指令的组成及应用中的种种注意事项也早已烂熟于心,但学生对数控编程也进入了一个相对“疲软”的时期。这时候进行宏程序的学习就容易在心理上有一种“懒散”的态度,似乎觉得宏程序就如同现阶段的编程一样是一件非常容易的事情,从而不能提起十分的精神去面对这门新的知识。而事实上很多学生在学习宏程序的过程中会慢慢的发现,宏程序的学习是一个系统的、循序渐进的过程,决不能掉以轻心。
要提高学生对宏程序的学习兴趣不妨从介绍宏程序的优势特点入手。宏程序最大的特点就是能比较轻松地编制非圆非直线曲线,而学生现阶段最引以自豪的却是那些标准的曲线[1]。于是在学习之前我要求学生编制一个非圆曲线。如图1。

图1 非圆曲线
学生在习惯了用G02、G03、G01编程的情况下,一般都会选择在该抛物线上找几个点,然后用画逼近圆的方法去找这样的圆弧编程,然而他们在编程的过程中会发现这样的圆弧既不好找,在编程的时候也很难计算节点,况且如果找的点越少在实际加工中误差也就越大。当学生在编制完该程序以后就会发现以前面所学的知识应用于该题就会非常的头痛,学生会迫不及待地想找到一种快捷而准确的方法来进行该曲线的编程,于是宏程序的概念就很自然地被引入。这样不但激发了学生的学习兴趣,而且在最初的理解学习过程中不会造成知识层面上的落差,能更快更好地去接受这个新的知识点。
二、以用代学,直达核心,明确学习的关键和重点
宏程序虽然并不是一门新的课程,但是其知识原理和学习方法与一般的数控编程加工不同,具有比较强的独立性。学生往往习惯性地将其与手工编程混在一起,一边比较一边学习。以华中系统为例,#0~#49当前局部变量、#50~#199全局变量。学生一开始接触到宏程序就会遇到宏变量和常量这些陌生的东西,由于以前并没有学习过与其相关的知识,对于这些变量就会觉得很茫然,不知道从什么地方入手。事实上从#0到#599这600个变量中,真正能用得上的非常有限,所以让学生全部理解和掌握这些变量的意义和用法完全没有必要。可以只要求他们理解和使用#0至#100这些变量,一方面降低了对学生和学习知识点掌握的要求,另一方面,宏程序的学习本身与实际使用结合得比较紧密,可以让学生明白所学即所用,以用代学的道理。
在学习宏程序之初,由于对这门新的课程不熟悉,再加上没有相关知识作为铺垫,学生往往会陷入迷茫的状态,很多学生由于找不着门路而大大降低了学习兴趣,并慢慢产生厌学情绪。所以宏程序的课程不能一味由程序到程序地讲述,而应该在授课的最初阶段就给学生展示出宏程序最核心的问题所在。首先让学生通过自己对数控车床与普通车床操作的对比找出两者的本质区别——坐标和刻度,然后引入宏程序编程与一般手工编程各自的关键所在(见图 2)[2]。
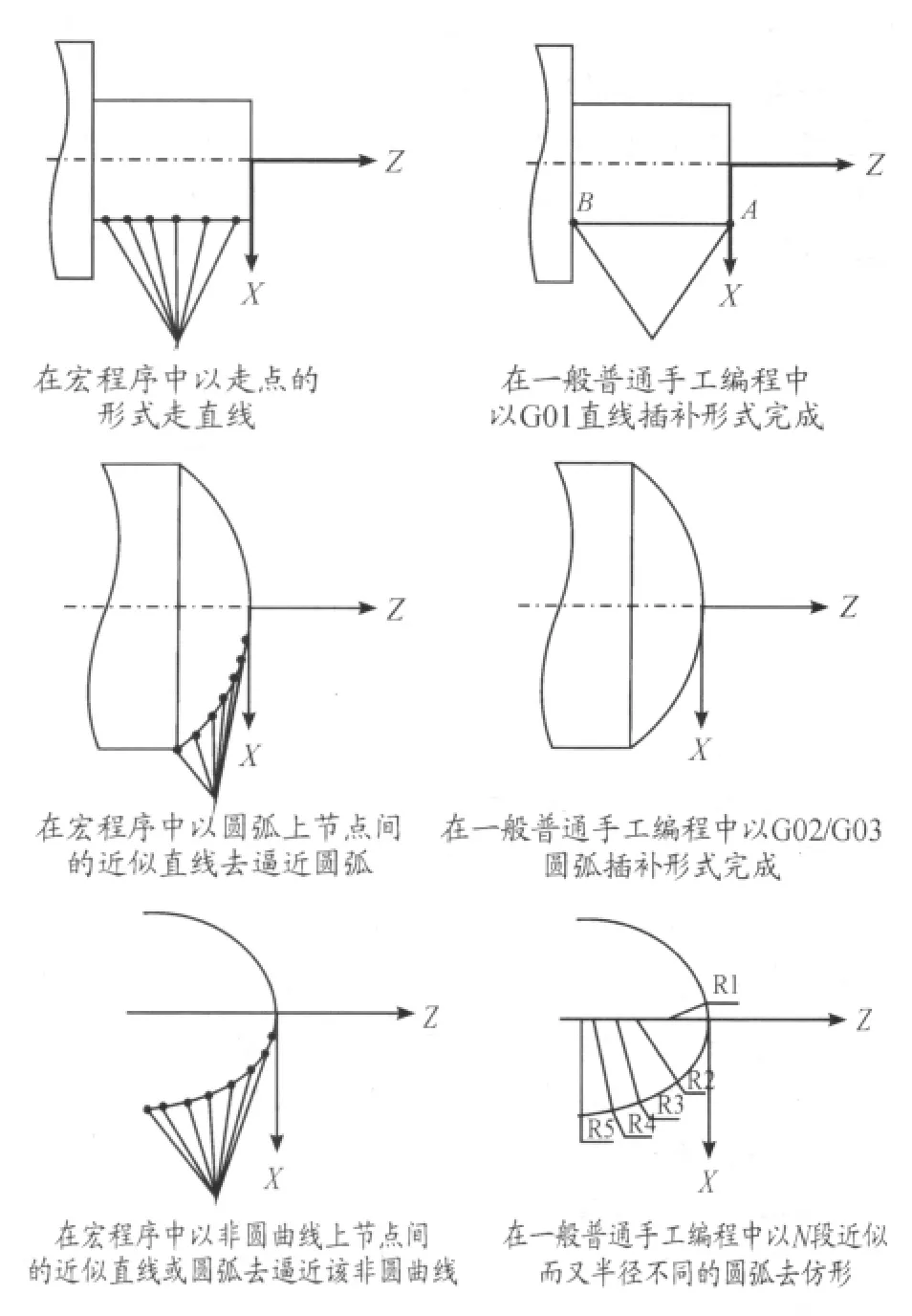
图2 数控车床与普通车床操作比较
从图2的比较中学生可以明白宏程序的关键之处在于节点的选择和控制,虽然普通数控编程也是用点的坐标去表达走刀路线,然而其在路线的表达方面,宏程序的编制比起普通编程所采用两种固定的表达方式来更为直观、准确,并且灵活多样。直观——圆弧归圆弧,曲线规曲线;准确——曲线的表达以该曲线的方程式为准;灵活多样——宏程序可以编制任意的曲线,而普通编程只有圆弧和直线两种表达样式。
三、简单的问题复杂化,复杂的问题简单化
就宏程序本身的编制过程而言,并不是一个简单的过程。与其他各种编程一样,不可能一步或者在很短的时间内就能掌握清楚。学习宏程序也不例外,必须从简单的编程开始。以编程中最简单的直线为例(如图3)。

图3 最简单的直线编程
1号工件轮廓在其所在的坐标中的方程式为X=10并且要求在-10≤Z≤0的范围内。于是该轮廓加工程序如图4。

图4 1号工件轮廓加工程序
2号工件轮廓在其所在的坐标中的方程式为Z=-X并且要求在10≤X≤15的范围内。于是该轮廓加工程序如图5。
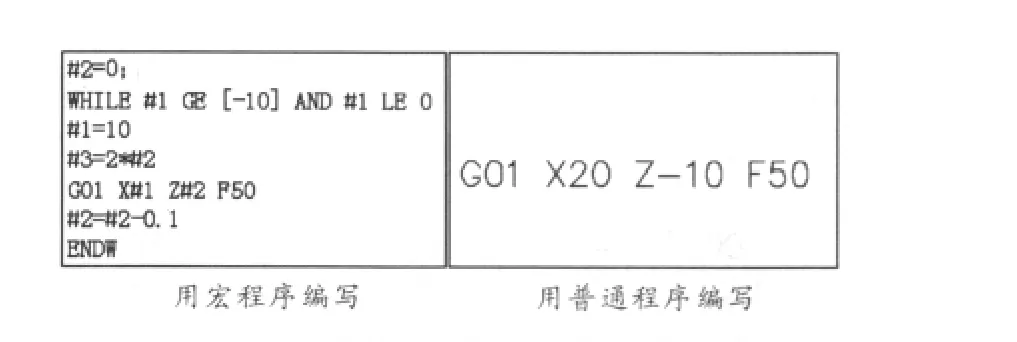
图5 2号工件轮廓加工程序
从图5两个工件轮廓的编程中可以发现对于最简单的直线编程,无论是台阶、断面还是斜面,所采用的一般普通编程方法都要比宏程序编程复杂很多。学生会想到,既然宏程序把这样一个很简单的问题复杂化,是不是完全没有学习和使用的必要了呢?在教学中应该对于学生这样的想法有充分的思想准备。首先要让学生明白学习宏程序不能否定也不能越过这复杂化的阶段,任何编程知识都是一步一步从基本的直线编制学起,宏程序也不会例外。时时刻刻提醒学生学习宏程序的最终目是什么,也可以图6这个例子给学生解释。
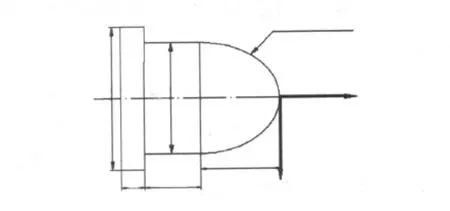
图6 用来编宏程序的曲线
图6的曲线要求不得少于20个节点去逼近。这时用宏程序编制出来(见图7)。

图7 曲线的宏程序
同样的图形,同样50个曲线上的节点,采用一般的编程方法则如图8。

图8 用一般方法编制的曲线程序
从上面两种不同的编程方式的对比中学生很容易发现,宏程序对于非圆曲线上节点的选取采用的是自加(即#1=#1+0.5)的形式,通过控制自加量(这里是0.5)来控制自加的次数从而达到控制节点数的目的,选取节点数的多少对编程没有任何影响,非常方便。而在一般的编程方式中由于没有类似于圆弧插补(G02/G03)这样的非圆曲线指令,不得不采用近似直线或者圆弧去逼近该非圆曲线的方法来编制程序。从上面的第二种编程中可以看出,尽管只完成了要求的一半即只选取了10个节点来逼近曲线,但是其节点的计算已经相当烦琐,如果随着节点数量的不断提升,这样的计算量和编程难度就会越来越大,非常不利于程序的编制[3]。并且要提醒学生对于这种逼近相似法,选取的节点越多,加工的准确度就越高,所以并不能以减少节点数量的方法来提高第二种普通编程的速度降低编程难度。
讲到这里,学生就会豁然开朗:宏程序的优点就是遇到无法用普通插补描述的曲线时,把显得非常烦琐的普通编程演变成一种比较固定简单的循环编程。这也就是将一个复杂的问题简单化的过程,也是宏程序的关键点所在。
四、宏程序编程中方法、过程的模块化
讲到这里,学生基本上已经将宏程序的关键重点及其特点掌握得差不多了,接下来学生不禁会出现这样的问题:宏程序的编制如何开始?
不错,与学习其他各种新知识中所遇到的问题一样,对于理论方面的讲授学生都能理解,但是一旦轮到他们自己实际去动手操作的时候,面对这样散乱的知识点,他们很难将其有条理地结合起来。所以不妨给学生一个标准的模块,他们按照这个模式走下去自然将各种方法和过程都理解清楚了。以图9这个圆弧的宏程序编制过程为例。
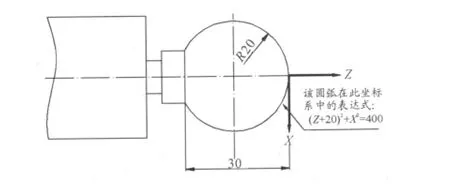
图9 用来编宏程序的圆弧
首先,写出该曲线(圆弧)的表达式。虽然在图8中已经告诉了学生,但是要求学生尽量自己去写出此表达式,并且必须将该表达式转化为或者的形式,其中要强调取值范围的重要性。以第二种表达式为例,从图8不难发现Z必须在[-30,0]的范围内。曲线的表达式在宏程序的编制过程中相当关键,一个好的表达式可以让宏程序简洁不少,也可以避免不少的错误[4]。所以,在教学的过程中一定要将表达式放在一个重要位置上去讲解,并且可以多安排一些关于方程表达式的练习,让学生熟能生巧。
其次,赋值。这里所要讲的赋值有两层含义:第一,将表达式中的变量与系统中的变量相结合。以华中系统为例:从#0开始直到#599这个600个变量中,首先得给X和Z进行定义,如把#1作为X变量,把#2作为Z变量。第二,将系统中的变量赋值。作为真正意义上的赋值,该步骤中将实际的值赋给#1或者#2也就是X或Z参数。由于选择了此种表达式,因此我们必须先给自变量Z进行赋值,从刀具的加工轨迹路线中不难看出,Z值的变化范围是从0起始直到-30结束的这一过程。因此首先将#2也就是Z变量赋值:#2=0。
再次,描述条件与表达式。既然选择了以Z为变量,就必须在描述条件的时候严格对其进行限制。即WHILE#2GE[-30]AND#2LE0。然后表达式跟上:当然,数控系统是不会识别这样的表达式的,所以先要将该表达式转化为系统能够识别的代码。由于每一种数控系统的宏程序代码编制不同就造成了各种运算式在优先等级和算法上有着很大的区别。如图10。
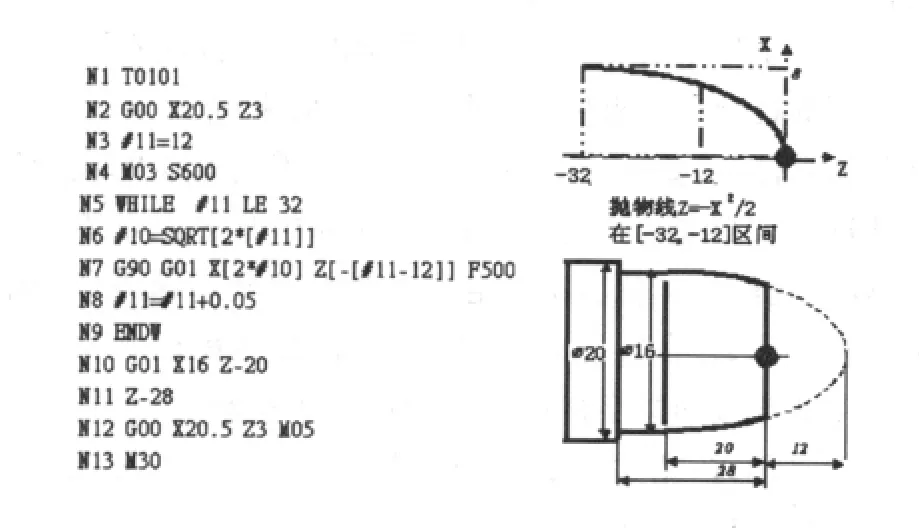
图10 用宏程序编制抛物线
因此,宏程序的编制,代码的转换过程一定要扎扎实实地完成,千万不可在中途尤其是在有分歧的算法上失误,进而影响到节点的误差乃至加工过程中的错误。
最后,使用逼近法编程和变量的自加过程。在上面的步骤中实现了节点的计算与表达,现在就是将这些节点连接起来从而实现对曲线的逼近。当然我们可以让学生自由去选择采用圆弧或者直线去逼近,也只有通过实际加工以后,他们才能明白这两种方法各自的优劣之处。变量的自加过程是宏程序编制的最后一步,也是宏程序对节点数量控制的关键所在。
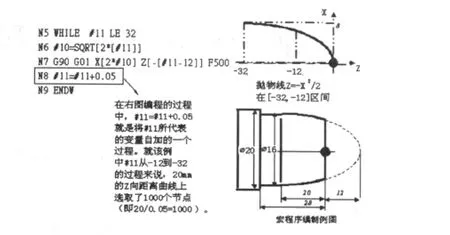
图11 控制宏程序节点数量
当然并不是节点越多越好,因为节点的计算是由系统自己完成的,如果节点过多必然会对系统造成拖累,从而减慢其速度,降低加工效率。
五、结束语
宏程序的教学其实并不是一件简单的事情,因此在指导学生学习宏程序的时候万万不可急于一时,无论是在教学过程和学生自己理解的过程中都不可以操之过急,学生只有在正确地将过程和方法理解和掌握之后才不会茫然和困惑。
[1]杨晓兰.华中系统宏程序编程[M].北京:机械工业出版社,2007.
[2]连赛英.数控编程技术[M].北京:机械工业出版社,2008.
[3]李善术.高级数控机床技术[M].北京:机械工业出版社,2007.
[4]李芝.宏程序的编程与应用[M].北京:机械工业出版社,2007.
(责任编辑 张佑法)
G712
B
1007-7111(2012)06-0062-04
2012-04-19
陈曦(1981—),男,讲师,研究方向:机械制造加工。
