一种改进的保护协调配合方法及其仿真研究

张 燃

(四川电力科学研究院，四川成都 610072)

0 引言

为满足电网对继电保护提出的可靠性、选择性、灵敏性和速动性要求，需要科学整定保护装置的定值，保证保护间的协调配合。然而随着电网规模的扩大，接线和运行方式日趋复杂，特别是大小环网相互重叠、长短线交错连接的状况，使后备保护定值相互依赖，构成配合关系环，难以合理配置;另外，近年来分布式发电逐渐兴起，其投退的不确定性也使保护配合十分复杂。因此，研究保护协调配合的计算和校验方法已成为一个亟待解决的问题。

国内外学者针对该问题已进行了大量研究［1－4］，特别是香港科技大学的So C.W.在其博士论文中提出一种保护配合TCM(time coordination method)方法［5］，并对其进行了细致的分析和计算。这里在TCM方法基础上进行改进，探讨了一种时间灵敏度优化配合(time sensitivity optimal coordination，TSOC)方法及其优化算法，并以一个配电网反时限过流保护配合为算例进行了仿真和分析，仿真结果表明该方法可根据系统特点和整定需要方便、量化地对保护性能选择进行适当折衷，具有很好的实用性和有效性。

1 时间灵敏度优化配合方法

保护协调配合研究从系统整体角度出发，建立数学模型，将全系统保护的协调配合问题转化为一组优化公式和约束条件来处理［6－11］。

1.1 TSOC 方法

选取继电保护时间级差约束违背数、故障持续时间、灵敏度约束违背数和配合对动作时间差与时间级差之差作为优化目标，以继电保护设备特性参数设置值作为TSOC方法的决策变量。

1.1.1 时间级差约束违背数

为使故障发生时保护动作具有选择性，停电范围尽量缩小，应满足保护配合对上游继电器与下游继电器动作时间之差大于给定的时间级差。故障时所有配合对时间级差违背数总和越小，则继电保护协调配合的综合性能越好。对于系统故障i，配合保护对j的上、下游保护装置动作时间之差定义为

其中，T_upi，j、T_downi，j为故障 i时配合对 j上、下游继电器的动作时间，定义时间级差约束违背数为

其中，grading_margin指时间级差，即保护配合对各自动作时间之差的最小值，考虑继电器操作、断路器动作、安全级差等，则选取固定的0.4 s。

考虑系统所有故障中全体保护协调配合，可得到时间级差约束违背总数为

其中，R表示继电保护特性参数设置值，即优化的决策变量。

1.1.2 故障持续时间

从系统发生故障到保护设备完全切断故障需要一定的时间，而短路电流持续时间越长，造成的后果越严重。以故障持续时间作为系统快速性指标进行优化，以达到使故障对系统的破坏最小的目的。

设故障i的故障时间为Fault_timei，该故障发生危害率为Pi，然后把所有故障情况相加得到一个故障时间的数学期望值。

1.1.3 灵敏度约束违背数

在后备保护之间，只有当动作时限和灵敏系数都相互配合时，才能切实地保证动作的选择性。灵敏度相互配合的要求是:对同一故障点而言，要求越靠近故障点的保护应具有越高的灵敏度，即在故障i发生时，对于保护配合对j，需满足

其中，Klm_upi，j和 Klm_downi，j分别为故障 i情况配合对j的上游和下游继电器的动作灵敏度;Klm_lim为灵敏度最小值，一般取1.2。与时间级差约束违背数类似，可定义灵敏度约束违背数及其总数为

1.1.4 保护配合对动作时间差与时间级差的差

在保证大于时间级差的情况下，为了保证保护设备的速动性，配合对动作时间差应尽可能的小，因此将各种故障情况下保护配合对的动作时间差与时间配合级差的差值总和最小作为一个优化目标。对所有故障和所有的保护配合对，该总和为

将以上4个指标的加权平均作为目标函数，可得到一个无条件单目标优化模型。

G(R)=min{αG1(R)μ+ βG2(R)+ γG3(R)θ+ λG4(R)}(9)其中，α、β、γ、λ称为权重系数，在0到1之间取值，分别代表了协调配合计算过程中对4个指标的偏好程度，满足α+β+γ+λ=1，可以根据不同对象、不同情况对其进行设定，从而能够方便、量化地根据不同特性系统特点和整定要求以及继保工程师的经验，对继电保护性能选择进行适当折衷。

1.2 优化方法

继电保护协调配合是典型动态环境下的复杂优化问题，选用文献［12］中所提出的速度跟踪粒子群优化算法求取式(9)的最优解，可克服传统算法收敛速度慢和易陷入局部最小的缺陷。

2 仿真算例及分析

2.1 仿真算例

文献［13］介绍了一种基于混杂Petri网的保护建模与仿真方法，利用该方法建立如图1所示的简单配电网络作为算例进行研究，各母线电压等级在图中标出，系统参数见文献［5］。

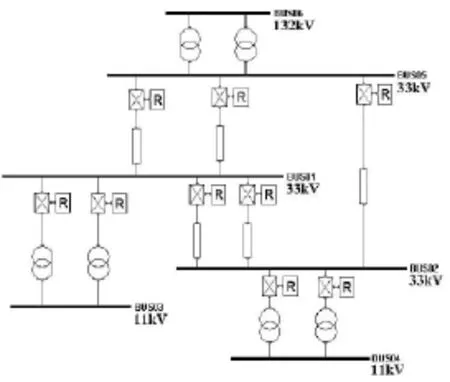
图1 保护协调配合算例模型

为了更明显地体现优化算法的效果，算例中采用时间整定为连续函数的反时限过流保护(inverse definite minimum time lag overcurrent relay，IDMTL OC)作为保护设备。根据IEEE C37.112－1996和 IEC 255－3标准，当故障电流恒定不变时，IDMTL OC的动作时间计算公式为

其中，A=0.14;p=0.02;TM 为时间整定系数;I为故障电流I_fault与保护启动电流定值的比，即

其中，CSM×CT_ratio×Relay_rating为启动电流值。

如果故障电流在保护装置启动后、动作前发生了改变，其动作时间满足

其中，T0为继电器实际动作时间。

2.2 计算结果

给定两组权重系数:如整定时要求尽可能保证保护准确配合，选择 α =0.4，β =0.1，γ =0.4，λ =0.1，称为权重(1);如果要求保护设备快速动作，选择α=0.1，β =0.3，γ =0.1，λ =0.5，称为权重(2)。

计算过程考虑母线 BUS01、BUS02、BUS03及BUS04发生三相短路故障情况，根据各母线电压等级，确定其故障危害率分别为1/3、1/3、1/6和1/6。短路故障发生时，仅考虑故障电流，不计负载电流。根据反时限保护的特性和短路计算结果具体化目标函数，并对速度跟踪粒子群优化算法参数进行初始化，设置粒子群规模为20，最大迭代次数为500，加速和惯性因子分别设置为c1=c2=2，wmax=0.8，wmin=0.2，其他参数按默认设置，分别对权重(1)和权重(2)两种情况进行计算，结果如表1到表4所示。

2.3 结果分析

由表1到表4所示的整定结果，可以得到:①设置权重为 α =0.4，β =0.1，γ =0.4，λ =0.1，主要是以保护设备时间和灵敏度的准确配合为目标，通过优化可得表1所示的定值，并计算得到表2所示各故障下保护设备的动作时间和灵敏度，可以看出时间约束违背系数和灵敏度约束违背系数均为0，即保证了各条母线发生三相短路故障时IDMTL OC都能正确动作;②而设置权重为 α =0.1，β =0.3，γ =0.1，λ =0.5，主要是考虑缩短保护动作时间和配合时间差，以尽快切除故障，由表4所示，保护动作时间和配合时间差均较权重(1)情况有一定缩短，且保证了灵敏度的正确配合，但在BUS03和BUS04故障时，某些配合对的动作时间差达不到0.4 s的要求。

表1 计算结果(α =0.4，β =0.1，γ =0.4，λ =0.1)

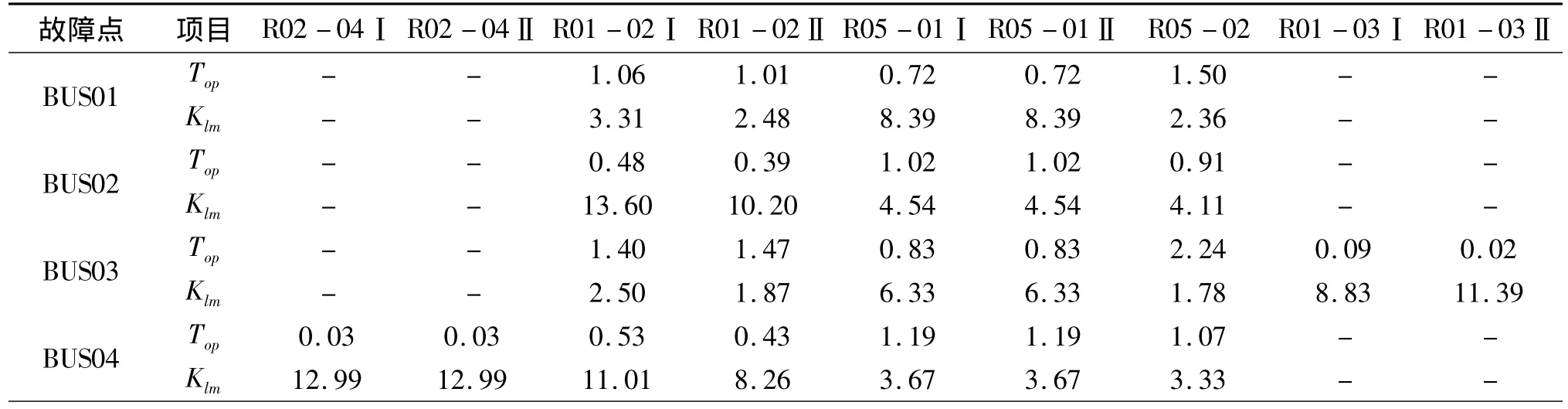
表2 动作时间(Top，单位:s)和灵敏度(Klm)(α =0.4，β =0.1，γ =0.4，λ =0.1)

表3 计算结果 (α =0.1，β =0.3，γ =0.1，λ =0.5)

表4 动作时间(Top，单位:s)和灵敏度(Klm)(α =0.1，β =0.3，γ =0.1，λ =0.5)

表5 过渡运行方式下各保护的动作时间(单位:s)和灵敏度

表6 网络结构改变情况下的各保动作时间

2.4 定值校验

在图1所示算例系统的各保护模型中设置表1所示的整定值，并设置母线BUS03三相永久性短路故障进行定值校验，故障开始时间为0.2 s，可得到如图2所示各保护流过的电流波形。

图2 各保护处的电流波形

从图2可以看出，故障发生后，流过各保护的电流均突然增大，保护R01－03Ⅱ延时最短(如表2所示)，经断路器延时后于0.272 ms切断线路LINE01－03Ⅱ，系统结构演变为图3所示的过渡运行方式。与LINE01－03Ⅱ平行的LINE01－03Ⅰ电流增大，而系统中其他线路电流均有所减小，从而使保护R01－03Ⅰ加速动作，切断故障母线BUS03，此后各线路电流恢复正常，其IDMTL OC保护由于未达到延时时间返回。

由仿真过程中可以看出，各保护中流过的电流由于网络结构改变而重新分配，在定值校验中应予以考虑。设保护装置在网络结构改变前流过的故障电流和延时时间分别为I－和T－(I－)，动作后故障电流和延时时间分别为I+和T+(I+)，忽略暂态过程，根据式(12)可得

其中，Tc和Ta表示网络结构改变时间和保护实际延时时间，变换式(13)得

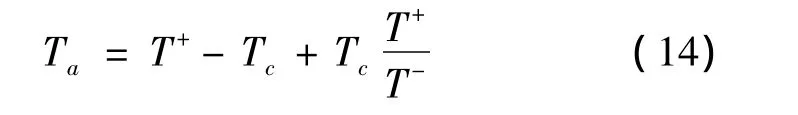
式(14)即为在IDMTL OC保护中故障电流改变时的延时时间计算公式。表5为在图3所示过渡运行方式下各保护的动作时间和灵敏度及其约束违背数，表6为网络结构发生改变时各保护动作时间及其约束违背数，可见，在两种情况下时间级差和灵敏度都可准确配合，满足选择、灵敏、可靠和快速性要求，协调配合的目标函数值可作为整定值评价的指标。

图3 过渡运行方式

3 结语

(1)提出了一种用于继电保护协调配合计算的时间灵敏度优化配合方法，该方法以时间级差约束违背数、故障持续时间、灵敏度约束违背数和配合对动作时间差与时间级差之差的加权和作为保护系统协调配合的优化目标，并采用速度跟踪粒子群算法对其进行优化计算。

(2)以一个配电网反时限过流保护配合为算例进行了计算和分析，其结果表明TSOC方法可根据系统特点和整定需要方便、量化地对继电保护性能选择进行适当折衷，具有很好的实用性和有效性;其目标函数值也可作为整定值评价的指标。

［1］IEEE PSRC Workin Group.Computer Aided Coordination of Line Protection Schemes［J］.IEEE Trans.on Power Delivery，1991，6(2):575 －583.

［2］Lee S J，Yoon S H，Yoon M C，et al.An Expert System for Protective Relay Setting of Transmission Systems［J］.IEEE Trans.on Power Delivery，1990，15(2):1202－1208.

［3］Bijoy C.An On－line Relay Coordination Algorithm for A-daptive Protection Using Linear Programming Technique［J］.IEEE Trans.On PWRD，1996，11(1):165 －171.

［4］Urdaneta A J，et al.Coordination of Directional Overcurrent Relay Timing Using Linear Programming［J］.IEEE Trans.On PWRD，1996，11(1):122－129.

［5］So C W.Intelligent Protection Coordination System［D］.The Hong Kong Polytechnic University，2001.

［6］So C W，Li K K，Li K T，et al.Application of Genetic Algorithm for Overcuurent Relay Coordination［C］.IEE 6th International Conference on Developments in Power System Protection，UK，Nottingham，1997.

［7］So C W，Li K K.Time Coordination Method for Power System Protection by Evolutionary Algorithm［C］.IEEE Industry Application Society Annual Meeting，Arizona，Phoenix，1999.

［8］So C W，Li K K.Overcurrent Relay Coordination by Evolutionary Programming［J］.International Journal of Electric Power System Research，2000，53(2):83－90.

［9］So C W，Li K K.Protection Relay Coordination on Ringfed Distribution Network with Distributed Generations［C］.Proceedings of IEEE TENCON’02，Beijing，China，2002.

［10］So C W，Li K K.Intelligent Method for Protection Coordination［C］.2004 IEEE International Conference on E-lectric Utility Deregulation，Restructuring and Power Technologies(DRPT2004)，Hong Kong，2004.

［11］So C W，Li K K.The Influence of Time Coordination Me－thod on Supply Reliability［C］.Conference Record of Industry Applications Conference，2000.

［12］杜新伟，刘涤尘，李媛.基于新型小波神经网络的电力故障回放技术［J］.电力系统自动化，2007，31(15):84－88.

［13］杜新伟，刘涤尘，袁荣湘，等.虚拟继电保护柔性建模仿真系统的研究［J］.电力系统自动化，2008，32(17):55－60.