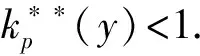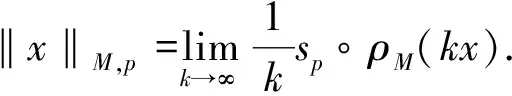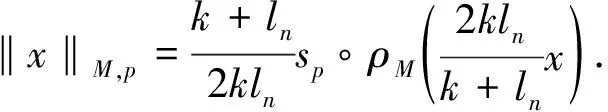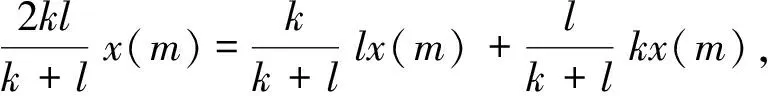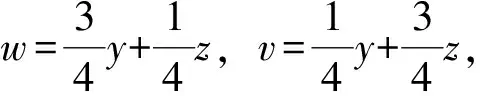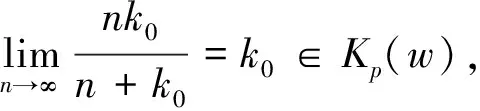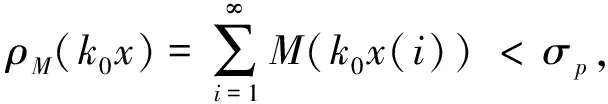赋p-Amemiya(1≤p≤∞范数的Orlicz序列空间的端点和严格凸性
2012-12-04段丽芬崔云安
段丽芬, 许 晶, 崔云安
(1. 通化师范学院 数学系, 吉林 通化 134002; 2. 哈尔滨理工大学 应用科学学院, 哈尔滨 150080)
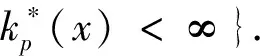
p-Amemiya(1≤p≤∞)范数[1]既包含了Orlicz范数[2](当p=1时), 又包含了Luxemburg范数[3](当p=∞时). 但当1 本文用X表示一个Banach空间,B(X)和S(X)分别表示X的闭单位球和单位球面. 定义1[8]x∈S(X)称为端点是指若x=(y+z)/2 (y,z∈B(X)), 则y=z. 用ExtB(X)表示B(X)所有端点构成的集合. 若ExtB(X)=S(X), 则称X是严格凸的. 定义2[9]若函数ρ:X→[0,∞)满足下列条件, 则ρ称为凸函数: 1) 当且仅当x=0时,ρ(x)=0; 2)ρ(-x)=ρ(x); 3) 对任何x,y∈X,a,b≥0,a+b=1, 都有ρ(ax+by)≤aρ(x)+bρ(y). 利用Minkowsky不等式易知,sp为非减的凸函数. 令σp=max{u≥0:sp(u)=1},εp=1-[1/p], 其中[1/p]表示不超过1/p的最大整数, 规定1/∞=0. 显然, 当1≤p<∞时,σp=0; 当p=∞时,σp=1. 当p=1时,εp=0; 当1 u 则当u θ:lM,p→[0,∞),θ(x)=inf{k>0:ρM(k-1x)<∞}; Ap:lM,p×(0,∞]→(0,∞],Ap(x,k)=k-1sp(ρM(kx)). 定义4[12]设M为Orlicz函数,u为实数. 如果对任何两个不同实数v,w, 只要(v+w)/2=u即有M(u)<(M(v)+M(w))/2, 则称u是M的一个严格凸点.M的严格凸点全体记为SCM. 显然,SCM⊂{u∈R:M(u)<∞}∪{±cM}. 定义5[12]如果存在常数k≥2和x0>0, 使得当x≤x0时,M(2x)≤kM(x), 则称Orlicz函数M(关于较小的x)满足Δ2条件. 引理1对任何1≤p≤∞及x=(x(i))i∈lM,p{0}, 都有: 引理3设1≤p≤∞, 则 引理1~引理4为文献[1]的平行结果, 其证明可完全平行获得(只要把函数改为序列即可), 故略. 定理1设1≤p≤∞, 则x=(x(i))i∈S(lM,p)是B(lM,p)的端点的充要条件是下列条件同时成立: 1) 若集合suppx={i∈N:x(i)≠0}中所含元的个数μ(suppx)≥2, 则 Ø; 2) ①{i=N:x(i)≠0}为单元集或②对任何k∈Kp(x), {kx(i):i=1,2,…}中至多有εp个元不属于SCM; 3) ①对任何k∈Kp(x),ρM(kx)≥σp或②对任何i∈N, 都有x(i)=cM<∞. 若条件1),2)及3)中①成立. 设x=(x(i))i∈S(lM,p),y,z∈B(lM,p),y+z=2x, 则‖y‖M,p=‖z‖M,p=1. 下面分三步证明y=z. 首先, 证明Kp(y)≠Ø,Kp(z)≠Ø时,y=z. 事实上, 记ky∈Kp(y),kz=Kp(z),k=kykz/(ky+kz), 利用引理1、sp和M的凸性及Minkowsky不等式, 有 这蕴涵‖x‖M,p=‖y‖M,p=‖z‖M,p=1=(2k)-1sp∘ρM(2kx), 所以, 2k∈Kp(x). 同时, 因为ρM(2kx)≥σp,sp(u)在[σp,∞)上严格递增, 故有 对任何正整数i, 利用M的凸性可得 当条件2)中①成立时, 设x={0,0,…,x(i),0,0,…}, 因为0∈SCM, 有y(j)=z(j)=0(j≠i). 注意到‖y‖M,p=‖z‖M,p=‖x‖M,p=1, 则y(i)=z(i)=x(i), 进而y(i)=z(i)=x(i). 故y=z. 当条件2)中②成立时, 注意到当1 可知对任何1≤p≤∞及正整数i, 都有kyy(i)=kzz(i). 又kyy(i),kzz(i),2kx(i)在同一个线性区间上, 且0∈SCM, 有kyy(i)=kzz(i), 进而kyy=kzz. 此外, ky=‖kyy‖M,p=sp(kyy)=sp(kzz)=‖kzz‖M,p=kz, 因此,y=z. 综上可得, 对任何x=(x(i))i∈S(lM,p), 若满足y,z∈B(lM,p),y+z=2x, 则必有y=z, 即x∈Ext(B(lM,p)). 充分性得证. 令y(i0)=x(i0)+u,z(i0)=x(i0)-u,y(i)=z(i)=x(i)(i≠i0),y+z=2x,y≠z, 但 同理‖z‖M,p≤1, 这与x∈Ext(B(lM,p))矛盾. 证毕. 推论1x=(x(i))i∈S(lM,p)是B(lM,p)的端点的充要条件是: 1)p=1且: ①若μ(suppx)≥2, 则K(x)≠Ø; ②若μ(suppx)=1或对任何k∈K(x)及i∈N, 都有kx(i)∈SCM; 2) 1 3)p=∞且: ①ρM(x)=1且μ{i∈N:x(i)∉SCM}≤1或②对任何i∈N, 都有x(i)=cM<∞. 定理2Orlicz序列空间lM,p严格凸的充要条件是: 1) 若x∈S(lM,p),μ(suppx)≥2, 则Kp(x)≠Ø; 2)M在[0,πM,p(1)]严格凸, 其中 πM,p(1)=inf{t>0: 2εpM(t)σp((2M(t))p-1N(p(t)))1-σp≥1}; 3) ①1≤p<∞或②p=∞且M∈Δ2. 证明: 结合文献[12]中定理2.7和定理2.9、 文献[4]中定理2的证明, 再利用定理1, 充分性及2)和3)的必要性易得, 1)的必要性可由引理4直接得到. 证毕. [1] CUI Yun-an, DUAN Li-fen, Hudzik H, et al. Basic Theory ofp-Amemiya Norm in Orlicz Spaces(1≤p≤∞): Extreme Points and Rotundity in Orlicz Spaces Endowed with These Norms [J]. Nonlinear Analysis: Theory, Methods & Applications, 2008, 69(5/6): 1796-1816. [2] Orlicz W. Über Eine Gewisse Klasse Von Räumen Vom Typus B [J]. Bull Acad Polonaise Sci: Ser A, 1932, 8: 207-220. [3] Luxemburg W A J. Banach Function Spaces [D]: [Ph D Thesis]. Delft: Delft University of Technology, 1955. [4] DUAN Li-fen, CUI Yun-an. Extreme and Strongly Extreme Points in Orlicz Sequence Spaces Equipped with the Generalized Orlicz Norm [J]. Journal of East China Normal University: Natural Science, 2009(1): 53-60. (段丽芬, 崔云安. 赋广义Orlicz范数的Orlicz序列空间的端点和强端点 [J]. 华东师范大学学报: 自然科学版, 2009(1): 53-60.) [5] DUAN Li-fen, CUI Yun-an. Extreme Points in Orlicz Space Equipped with the Generalized Orlicz Norm [J]. Journal of Zhejiang University: Science Edition, 2007, 34(3): 252-256. (段丽芬, 崔云安. 赋广义Orlicz范数的Orlicz空间的端点 [J]. 浙江大学学报: 理学版, 2007, 34(3): 252-256.) [6] DUAN Li-fen, CUI Yun-an. Strongly Extreme Points in Orlicz Space Equipped with the Generalized Orlicz Norm [J]. Journal of Zhejiang University: Science Edition, 2009, 36(1): 6-11. (段丽芬, 崔云安. 赋广义Orlicz范数的Orlicz空间的强端点 [J]. 浙江大学学报: 理学版, 2009, 36(1): 6-11.) [7] DUAN Li-fen, XU Jing, CUI Yun-an. Uniform Rotundity in Orlicz Function Spaces Equipped with the Generalized Orlicz Norm [J]. Journal of Jilin University: Science Edition, 2011, 49(5): 809-813. (段丽芬, 许晶, 崔云安. 赋广义Orlicz范数的Orlicz空间的一致凸性 [J]. 吉林大学学报: 理学版, 2011, 49(5): 809-813.) [8] 俞鑫泰. Banach空间几何理论 [M]. 上海: 华东师范大学出版社, 1986. [9] Maligranda L. Orlicz Spaces and Interpolation [M]. Campinas: Universidade Estadual de Lampinas, 1989. [10] CUI Yun-an, Hudzik H, Nowak M, et al. Some Geometric Properties in Orlicz Sequence Spaces Equipped with Orlicz Norm [J]. Journal of Convex Analysis, 1999, 6(1): 91-113. [11] Orlicz W. A Note on Modular Spaces [J]. Bull Acad Polon Sci Math, 1961, 9(1): 157-162. [12] Chen S T. Geometry of Orlicz Spaces [M]. Warszawa: Dissertations Math, 1996.1 预备知识
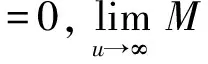
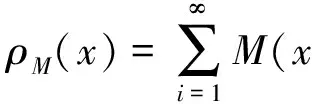
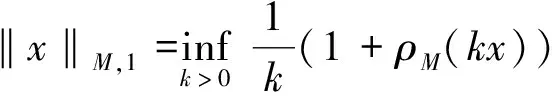
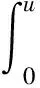
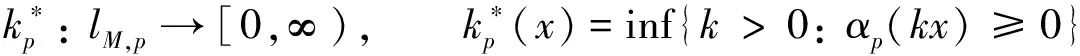
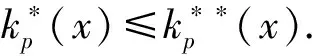
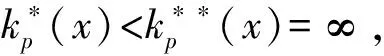
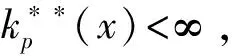
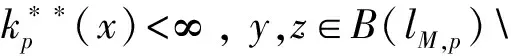
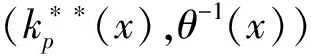
2 主要结果