直觉模糊最小二乘支持向量机*

郭新辰, 张 超, 李成龙

(东北电力大学 理学院, 吉林 吉林 132012)

支持向量机(SVM)是在VC维理论和结构风险最小化原理基础上发展的一种通用机器学习方法[1]. 为提高SVM的训练效率, Suykens等[2-3]对标准SVM进行了扩展, 提出了最小二乘支持向量机(LS-SVM), 采用具有等式约束且满足KKT条件的规则化最小二乘函数作为损失函数, 代替了SVM计算复杂的QP问题, 求解速度相对较快. 但由于平方损失函数没有正则化, 导致最小二乘向量机对孤立点的鲁棒性较差[4-5].

为了克服噪声和野点对支持向量机的影响, 文献[6]将模糊集理论和支持向量机相结合, 提出了模糊支持向量机(FSVM). 文献[7-10]将二者结合又提出了模糊最小二乘支持向量机(FLS-SVM). 在样本的隶属度确定方面, 常见的方法是根据样本到类中心的距离确定相应的隶属度大小, 但这种方法所确定的隶属度有两点局限性： 1) 未考虑样本间的紧密程度； 2) 未考虑样本周围的样本点情况.

Zadeh[11]提出了模糊集理论, 但由于其隶属度是一个实数, 只能反映支持、 不支持和不确定三者之一, 不能反映实际情况. 因此, Atanassov[12]在模糊集的基础上提出了基于隶属度、 非隶属度和不确定度的直觉模糊集. 本文将直觉模糊集的相关理论引入到最小二乘支持向量机中提出了新的直觉模糊最小二乘支持向量机(intuitionistic fuzzy least square support vector machine, IFLS-SVM).

1 直觉模糊集

设χ为给定的论域, 则定义χ上的直觉模糊集为

A={〈x,μA(x),νA(x)〉x∈χ},

其中μA(x):x→[0,1]和νA(x):x→[0,1]分别为A的隶属度函数和非隶属度函数, 并满足对所有的x∈A均有0≤μA(x)+νA(x)≤1成立.πA=1-(μA(x)+νA(x))称为x属于A的不确定度函数, 即直觉指数.

2 最小二乘支持向量机与模糊最小二乘支持向量机

给定带有类别标签的训练集(x1,y1),(x2,y2),…,(xl,yl), 其中训练样本xi∈RN,yi∈{1,-1}为训练样本对应的类标签,i=1,2,…,l. LS-SVM对应的优化问题为

(1)

其中：φ(x): RN→ RNh为输入空间到特征空间的映射； 权矢量wT∈RN； 误差变量ξi∈R；b为偏差量；C为正规化参数即最大分类间隔与最小分类误差的折中.

若在FLS-SVM中引入隶属度μi的概念, 则相关的数学模型变为

(2)

3 直觉模糊最小二乘支持向量机

给定带有类别标签的训练集(以样本有两类为例)： (x1,y1),(x2,y2),…,(xl,yl), 其中: 训练样本xi∈RN;yi∈{1,-1}为训练样本对应的类标签;i=1,2,…,l.

3.1 相关指标

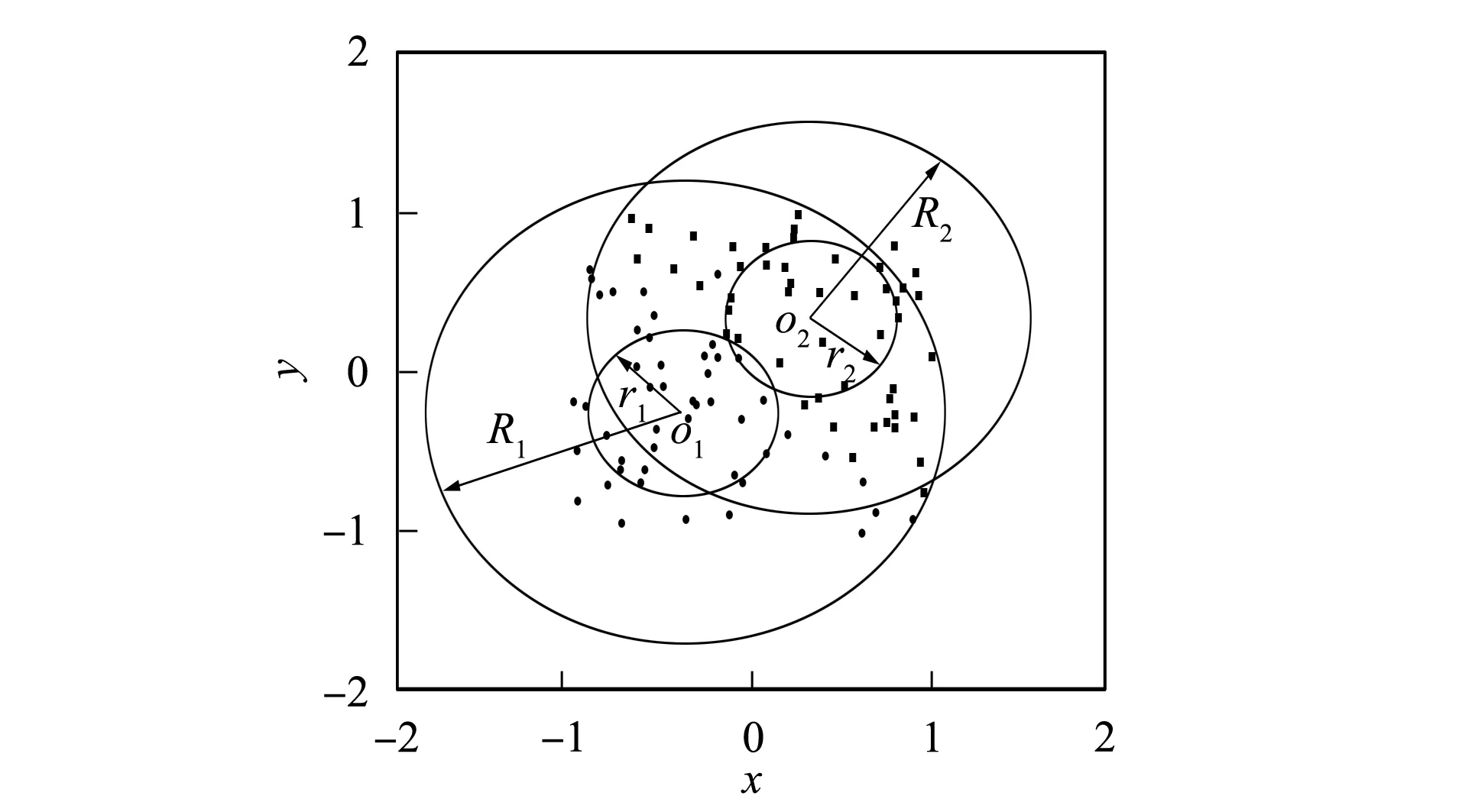
图1 样本类中心与类内、 外径示意图Fig.1 Diagram of sample class center and internal and external radii

3.1.2 样本点周围同类点比例与异类点比例 正样本点周围同类点比例为

负样本点周围同类点比例为

负样本点周围异类点比例为

d值需要综合考虑R1,r1,R2,r2和正负样本容量等指标合理取值[13].

3.1.3 样本隶属度 为了更好地反映每个样本点与类别间的真实关系, 定义相关的隶属度. 正样本属于正类隶属度为

正样本属于负类隶属度为

当样本点满足D(xi,O1)

负样本属于负类隶属度为

负样本属于正类隶属度为

由隶属度的计算公式可得：

3.2 直觉模糊最小二乘支持向量机

因为直觉指数反映了一个样本的不确定程度, 所以直觉模糊最小二乘支持向量机模型为

(3)

其中k为待定参数, 满足0≤μi-k·πi≤1.

模型(3)对应的Lagrange函数为

(4)

其中Lagrange乘子αi∈R,i=1,2,…,l. 根据KKT条件, 有

(5)

其中i=1,2,…,l. 将式(5)写成矩阵形式为

(6)

其中:

Z=(y1φ(x1),y2φ(x2),…,ylφ(xl));y=(y1,y2,…,yl);μ=diag(μ1,μ2,…,μl);

π=diag(π1,π2,…,πl);ξ=(ξ1,ξ2,…,ξl)T;α=(α1,α2,…,αl)T;1=(1,1,…,1)T.

经同解变换消去变量w和ξ, 并结合Mercer条件, 式(4)可写成

(7)

其中Ωij=yiyjK(xi,xj). 令A=Ω+(C(μ-k·π))-1, 求解式(7)可得

4 仿真实验

借助MATLAB的LSSVMlab工具箱, 在人工数据集上对本文算法进行实验验证. 验证过程如下.

1) 随机生成人工数据集. 样本容量为300, 取其中100个样本作为训练样本集, 其余200个样本作为测试集.

2) 对训练样本集进行训练. 训练采用RBF核函数, 取σ=0.5,C=10,d=0.6,k=0.5. 分别用LS-SVM,FLS-SVM和IFLS-SVM这3种方法对训练样本集进行训练.

3) 根据3种训练结果分别对测试集进行测试.

4) 对测试结果进行整理. 由于每次训练时训练集和测试集均为随机生成, 所以本文取3种方法测试100次准确率的平均值作为测试准确率.

根据上述训练过程, 得出3种方法的测试准确率结果分别为LS-SVM： 93.75%; FLS-SVM： 94.45%; IFLS-SVM： 95.25%. 可见IFLS-SVM的分类效果较好. 图2为IFLS-SVM(图2(A))和FLS-SVM(图2(B))对同一组数据分类结果的对比. 由图2可见, FLS-SVM将右下方的一个样本点分错, 而IFLS-SVM 则没有. 因此, 本文提出的IFLS-SVM算法比较合理.

图2 直觉模糊最小二乘支持向量机和模糊最小二乘支持向量机分类的对比结果Fig.2 Classification by IFLS-SVM and FLS-SVM

为了进一步验证IFLS-SVM算法的有效性, 在标准数据集Blood-Transfusion, Pima Indians Diabetes和Statlog (Heart)上对LS-SVM, FLS-SVM和IFLS-SVM这3种算法进行对比测试, 测试结果列于表1. 由表1可见, IFLS-SVM算法对应的准确率较高, 从而进一步验证了IFLS-SVM算法的合理性.

表1 3种算法在标准数据集上的测试结果

综上所述, 为了降低在采用LS-SVM分类时样本中噪声和野点对分类效果的影响, 本文将直觉模糊集的相关理论引入到LS-SVM中, 建立了直觉模糊最小二乘支持向量机. 先定义了样本的隶属度、 非隶属度及直觉指数等相关指标, 并建立了IFLS-SVM的数学模型, 再对其求解过程进行推导, 最后通过在人工数据集和标准数据集上进行仿真实验, 实验结果验证了算法的有效性.

[1] Vapnik V N. Statistical Learning Theory [M]. New York: Wiley, 1995： 100-105.

[2] Suykens J A K. Nonlinear Modeling and Support Vector Machines [C]//Proceedings of the 18th IEEE Instrumentation and Measurement Technology Conference. Budapest: Hungary, 2001： 287-294.

[3] Suykens J A K, Vandewalle J. Least Squares Support Vector Machine Classifiers [J]. Neural Process Lett, 1999, 9(3)： 293-300.

[4] Shim J Y, Hwang C, Nau S. Robust LS-SVM Regression Using FuzzyC-Means Clustering [J]. Advances in Natural Computation, 2006, 1(1): 157-166.

[5] LI Jin, TANG Wei. Fuzzy Least Squares Support Vector Machine in the Black Liquor Baume Soft Measurement [J]. Aerospace Manufacturing Technology, 2008(2): 51-53. (李瑾, 汤伟. 模糊最小二乘支持向量机在黑液波美度软测量中的应用 [J]. 航天制造技术, 2008(2): 51-53.)

[6] LIN Chun-fu, WANG Sheng-de. Fuzzy Support Vector Machines [J]. IEEE Transactions on Neural Networks, 2002, 13(2): 464-471.

[7] CHEN Xiu-juan, LI Yong, Robert H G, et al. Genetic Fuzzy Classification Fusion of Multiple SVMs for Biomedical Data [J]. Journal of Intelligent & Fuzzy Systems, 2007, 18(6): 527-541.

[8] YANG Jun, DUAN Chong, XIE Shou-sheng. Fuzzy Least Squares Support Vector Machines Based Recognition for Aircraft Flight Action [J]. Missiles and Guidance, 2004, 24(3): 395-398. (杨俊, 段翀, 谢寿生. 基于模糊最小二乘支持向量机的飞机飞行动作识别 [J]. 弹箭与制导学报, 2004, 24(3): 395-398.)

[9] ZHANG Ying, SU Hong-ye, CHU Jian. Soft Sensor Modeling Based on Fuzzy Least Squares Support Vector Machine [J]. Control and Decision, 2005, 20(6): 621-624. (张英, 苏宏业, 褚健. 基于模糊最小二乘支持向量机的软测量建模 [J]. 控制与决策, 2005, 20(6): 621-624.)

[10] WEI Guo, LIU Jian, SUN Jin-wei, et al. Study on Nonlinear Multifunctional Sensor Signal Reconstruction Method Based on LS-SVM [J]. Acta Automatica Sinica, 2008, 34(8): 869-875. (魏国, 刘剑, 孙金玮, 等. 基于LS-SVM的非线性多功能传感器信号重构方法研究 [J]. 自动化学报, 2008, 34(8): 869-875.)

[11] Zadeh L A. Fuzzy Sets [J]. Information and Control, 1965, 8(3): 338-353.

[12] Atanassov K T. Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96.

[13] HA Ming-hu, HUANG Shu, WANG Chao, et al. Intuitionistic Fuzzy Support Vector Machine [J]. Journal of Hebei University: Natural Sicence Edition, 2011, 31(3): 225-229. (哈明虎, 黄澍, 王超, 等. 直觉模糊支持向量机 [J]. 河北大学学报: 自然科学版, 2011, 31(3): 225-229.)