一类具奇异项和梯度项的拟线性椭圆方程正解的不存在性

景元萍, 郭 斌, 张永胜

(1. 洛阳理工学院 数理部, 河南 洛阳 471023; 2. 吉林大学 数学研究所, 长春 130012)

0 引 言

考虑如下边值问题:

(1)

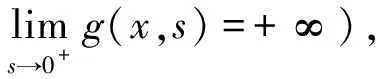
当p=2时, 对边值问题

(2)

的研究目前已有许多结果[1-7]. 当g(x,u)为非奇异的情形时, Bensoussan和Boccardo等[1-2]对g(x,u)是Ω×(0,+∞)上Carathédory函数的情形进行了研究. 对g(x,u)具有奇异点的情形, Arcoya等[3-4]证明了当g(x,u)=u-γ(0<γ≤1)时问题(2)解的存在性. 之后, Arcoya等[5]又对一般情形的g(x,u)研究了问题(2)解的性质, 给出了解的存在条件. 对于更一般的非线性算子(p-Laplace算子), 文献[6-7]研究了该类问题解的存在性. 基于上述研究结果, 本文通过巧妙设计检验函数, 并借助p-Laplace算子在加权函数下的第一特征值, 获得了问题(1)有限能量解的不存在结果.

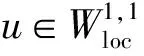
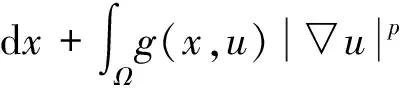
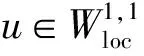
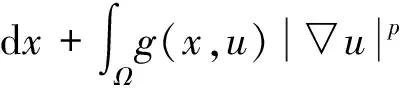
(3)

1 主要结果

定理1设f∈Lr(Ω)(r≥N/p),f≥0,f≠0. 若下列条件成立, 则问题(1)不存在正的有限能量解:

(H1) 存在非负函数h∈C[(0,+∞),[0,+∞)), 满足

(H2) 0≤h(s)≤g(x,s) a.e.x∈Ω, ∀s>0,h(s)=0,s>1.

引理1假设λ(f)是特征值问题

(4)

引理1的证明可参见文献[8].

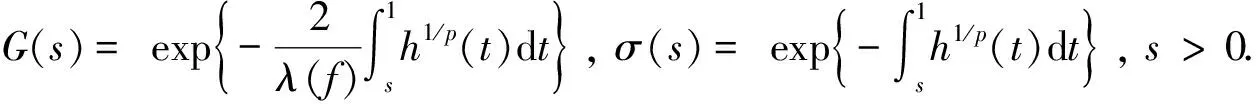
根据假设(H1), 易证:σ∈C1([0,+∞)),σ′(0)=h0,σ(s)=0 ⟺s=0;σ(s)=1,s>1;σ(s)≤1,s≤1;σ′(s)=σ(s)h1/p(s),G′(s)=[2/λ(f)]G(s)h(s).

引理2假设(H1)成立, 则函数

在[0,+∞)上连续可微, 且满足方程

进一步,φ满足不等式:φ(s)≤[λ(f)/2]σp(s), ∀s>0.

证明: 只需证明φ(s)在s=0点连续可微. 由于G(t)单调递增, 因此

所以φ(s)在s=0点连续. 下面证明φ(s)在s=0点可微.

从而φ(s)在[0,+∞)上连续可微.

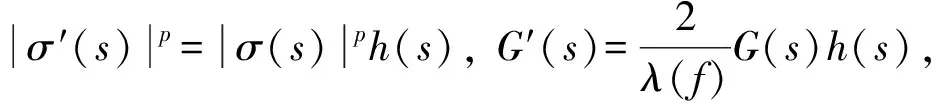
(5)

根据假设条件(H2), 可得

(6)

结合引理2, 有

(7)

[1] Bensoussan A, Boccardo L, Murat F. On a Nonlinear Partial Differential Equation Having Natural Growth Terms and Unbounded Solution [J]. Ann Inst H Poincaré Anal Nonlinéaire, 1988, 5(4): 347-364.

[3] Arcoya D, Barile S, Martínez-Aparicio P J. Singular Quasilinear Equations with Quadratic Growth in the Gradient without Sign Condition [J]. J Math Anal Appl, 2009, 350(1): 401-408.

[4] Arcoya D, Martínez-Aparicio P J. Quasilinear Equations with Natural Growth [J]. Rev Mat Iberoamericana, 2008, 24(2): 597-616.

[5] Arcoya D, Carmona J, Leonori T. Existence and Nonexistence of Solutions for Singular Quadratic Quasilinear Equations [J]. J Differential Equations, 2009, 246(10): 4006-4042.

[6] YUAN Hong-jun, CHEN Ming-tao. Some Notes on the Positive Solutions for a Class of Quasi-linear Elliptic Equations with Degeneracy and Singularity [J]. Journal of Jilin University: Science Edition, 2005, 43(6): 741-745. (袁洪君, 陈明涛. 一类具有退化性和奇异性的拟线性椭圆方程正解的注记 [J]. 吉林大学学报: 理学版, 2005, 43(6): 741-745.)

[7] WEI Xiao-dan. Existence and Multiplicity of Solutions for a Nonlinear Singular Elliptic Equation [J]. Journal of Jilin University: Science Edition, 2008, 46(4): 653-654. (魏晓丹. 一类非线性奇异椭圆方程解的存在性和多重性 [J]. 吉林大学学报: 理学版, 2008, 46(4): 653-654.)

[8] Arcoya D, Ruiz D. The Ambrosetti-Prodi Problem for thep-Laplace Operator [J]. Commu Partial Diff Equa, 2006, 31(6): 849-865.