机载激光扫描中复杂建筑物轮廓线平差提取模型

刘 春，李 楠，吴杭彬，杨 璇

（1.同济大学 测绘与地理信息学院，上海200092；2.同济大学 现代工程测量国家测绘地理局重点实验室，上海200092）

机载激光扫描（light detection and ranging，LiDAR）作为快速发展的新兴测量技术，已引起人们的广泛关注，且成为国内外研究开发的热点技术之一.由机载激光扫描系统获取的大范围高精度的3维点云，被应用于地面模型［1］，城市表面模型［2］，房屋重建［3］等诸多领域.其中，建筑物轮廓线提取是城市制图和建立3维建筑模型的基础，从LiDAR 数据中获取精确建筑物轮廓线是至关重要的研究内容.由于LiDAR 原始数据是离散的3维点云，属于同一个建筑面的3维激光脚点是随机分布的，没有明确的轮廓线，再加上建筑本身形状的复杂和多样性，所以造成了从LiDAR 数据提取建筑物轮廓线的困难.

目前，机载激光扫描数据的建筑物轮廓线提取研究成果主要分为基于栅格化的提取方法和基于点云空间结构的提取方法.采用点云数据来提取建筑物轮廓的方法一般是将LiDAR 点云栅格化为深度影像图，再利用图像的分割算法及边界线提取算法等图像分析手段实现轮廓线提取.如吴杭彬等［4］采用数学形态学中的膨胀和腐蚀方法进行序贯运算，再将建筑物边缘矢量化得到每个地物所对应的矢量边缘和数据点，尤红建等［5］对激光点进行二次内插加密生成DSM（digital surface model）影像数据，以图像处理的方法提取建筑物轮廓.这些方法将LiDAR 点云处理为灰度图像，处理速度快、方法简单明了，然而栅格化处理过程会引入新的误差，从而限制了处理结果的精度.

更多研究则趋向于基于离散激光点云的空间结构，TIN（triangulation irregular network）模型和Alpha Shapes算法等.Maas等［6］采用TIN 构建点云的空间拓扑关系，对所有三角面元进行聚类分析检测平面屋顶，以屋顶面与墙面的交线为房屋边线提取建筑物轮廓线.曾齐红等［7］以屋顶LiDAR 的TIN 的外围三角形边作为边界点，再通过扩展简化与规则化得到屋顶边界最终轮廓线模型.Lach［8］和沈蔚等［9］采用Alpha Shapes算法从无序点集中进行几何形状的重建进而提取，简化轮廓线，然后通过矩形外接圆和分类强制正交法分别对四边形和多边形建筑物轮廓线进行规则化.Aparajithan等［10］通过改善的凸壳算法，从LiDAR 点云中提取边界轮廓线，再利用边界线之间的垂直关系平差优化初始边界线.

可见，目前已有的这些算法仅针对含有直线段的简单多边形建筑物，然而复杂建筑物的平面形状不仅局限于多边形，还包含有圆弧线段，已有方法并没有考虑含有圆弧的复杂建筑物轮廓线.因此本文针对城市里的复杂建筑物，即轮廓线中不仅含有直线段还包含圆弧线段的不规则建筑物，基于离散点的空间结构分析，提取包含圆弧线段在内的建筑物的真实轮廓线，并采用平差优化调整初始轮廓线，得到规则化的建筑物轮廓线.本文方法的流程如图1所示.

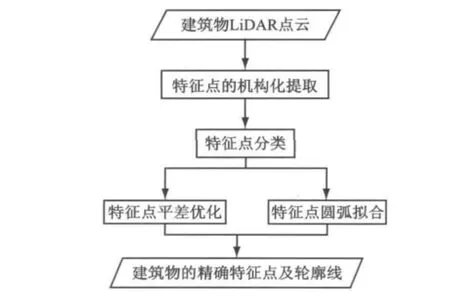
图1 提取轮廓线流程图Fig.1 The flowchat of boundary extraction

1 建筑物特征点的结构化提取

1.1 边界点和初步轮廓线提取

本文首先对建筑物屋顶点构建不规则三角网，再通过三角形边长比约束条件提取建筑物的凹形边界.不规则三角网只能反映凸边形的边界，建筑物凹角处的冗余三角形不能正确反映建筑物形状，由分布均匀的离散点构建的不规则三角网中的三角形应满足等边三角形的原则，而凹角处离散点分布不均匀，会出现不稳定的三角形，也就是有边长过长的三角形.所以本文采用三角形的边长比约束条件，去除冗余三角形得到符合实际情况的边界.通过大量实例数据反复验证，稳定三角形的边长比一般阈值在1.8左右，当三角形内最长边跟最短边比大于阈值时，该三角形位于凹角处而非建筑物内部，删除该类三角形后所得到的三角网才能正确反映建筑物形状.

采用边长约束的不规则三角网构建的屋顶三角网，在此基础上分析边界边与非边界边的差别，得到判别规则：边界边仅存在于一个三角形内；非边界边同时在两个三角形内，是两个三角形的公共边.通过对不规则三角网中三角形的筛选，可得屋顶边界点.

1.2 初步轮廓线的特征点提取

Dougls＿Peucker是曲线简化的经典算法，其基本思想是：将曲线首点P0、末点Pn两点连线，一次计算首尾两点之间的所有中间点（P1，P2，P3，…）到该线段的距离，找出距离最大的点，并判断该距离是否小于给定的距离阈值，若是，则舍去所有中间点；否则，保留该点，并以该点为界，将曲线分为两部分，然后对这两部分重复以上操作［11］.也就是当曲线被新找到的中间点分为两部分后，将这两部分分别作为独立曲线重复以上步骤，直到所有中间点到线段距离小于阈值.如图2所示，dmax为到该直线段内的最大距离.

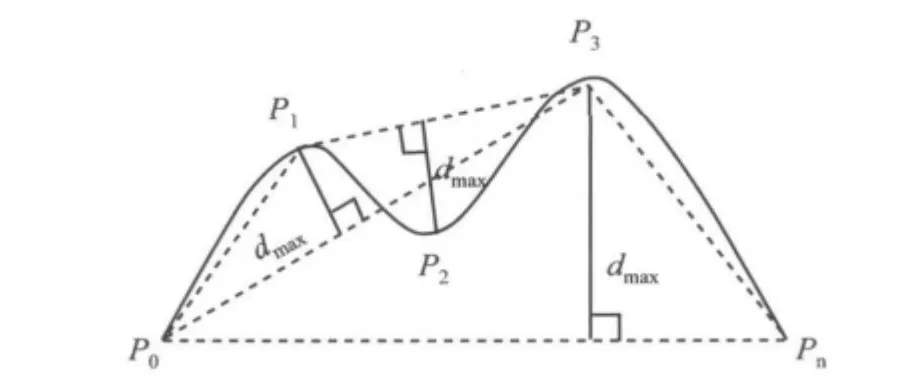
图2 Douglas算法示意图Fig.2 Schematic diagram of douglas algorithmic

房屋屋顶边界点可看作一条封闭的曲线，本文应用改进的Douglas＿Peucker方法抽稀曲线点［12］得到特征点.首先将距离边界重心点最远的两点作为初始特征点并连线，计算剩余的边界点到该线段的距离，取距离最远点作为新的特征点，再将新特征点两两连线，重新计算线段内点到直线的距离，距离大于阈值的点即作为特征点，重复以上步骤直到所有中间点到线段距离小于阈值.

该算法中的阈值参数大小直接影响特征点提取结果，如果阈值过大，提取到的特征点个数较少，可能无法准确反映建筑物真实的轮廓特征；如果阈值过小，会导致本应属于同一条直线的点被误判为特征点，使特征点集冗余.针对不同LiDAR 点云数据的空间结构特性，设置合适的距离阈值才能提取出较为准确的特征点.本文中距离阈值为1.5倍的平均点间距，并通过不同数据实例验证，该阈值能从LiDAR 点云中取得较为理想的特征点.

1.3 特征点分类识别

传统方法处理的建筑物数据是仅具有直线段的建筑，处理带有弧段的建筑物数据还存在一定的缺陷.针对此类建筑物，提取出的特征点可被分为3类：两垂直边界线的交点，即直角点；弧线特征明显的点，即弧线点；非直角点也非弧线点的轮廓线的转折点，称为一般点.准确识别出直角点、弧线点和一般点，才能根据各自不同几何形状特征，进一步拟合优化轮廓线.本文采用相邻点夹角判别方法识别特征点，流程如图3所示.

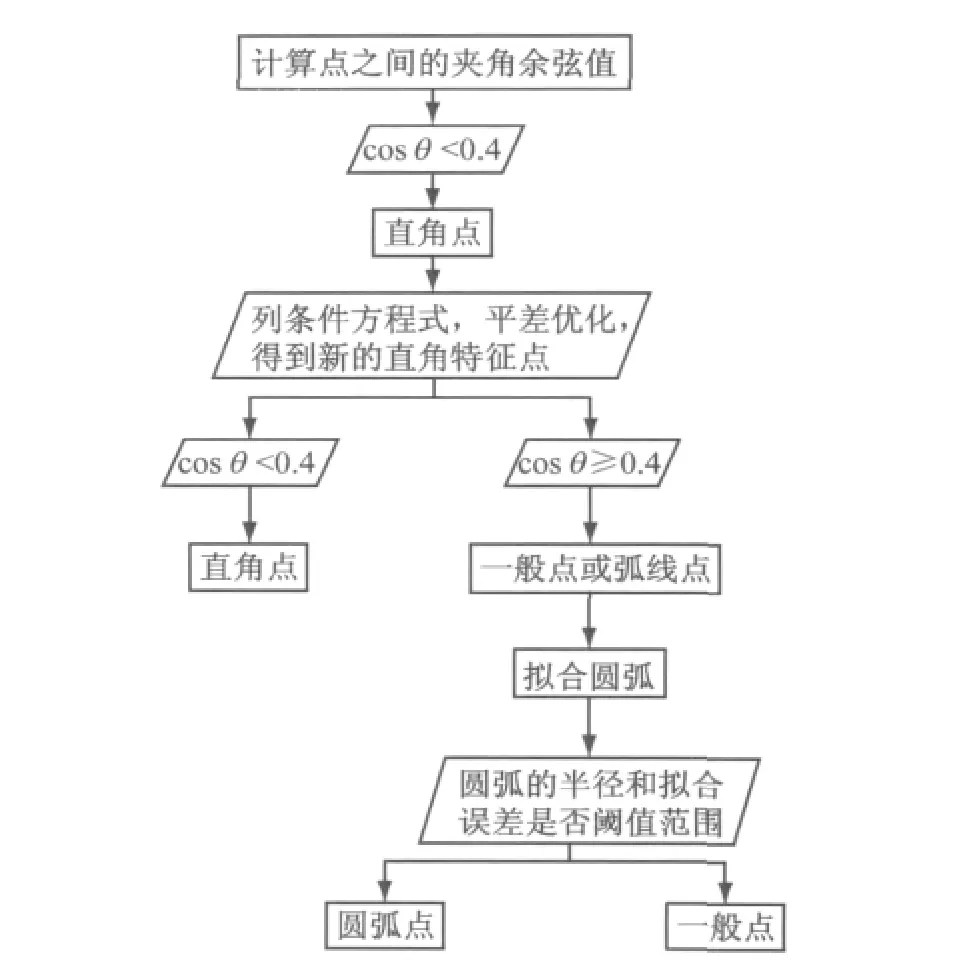
图3 特征点分类流程图Fig.3 The flowchart of feature points classification

边界点中的n个特征点将边界线分成n部分，识别特征点的过程也就是判断每一部分的边界点代表是一条直线还是一段圆弧线.由于直角点位于轮廓线上转折角90°的位置，有明显的直角特征，所以首先从特征点中筛选出直角点.图4描述了相邻点构成向量的夹角θ，图中P1，P2和P3为相邻3个特征点，θ为过点P2的两条边界线的变化角，即两个向量的夹角.根据夹角θ进行判断，当θ与90°之差小于阈值时认为该特征点位于直角拐点的位置，也就是初始直角点，由于LiDAR 点云分布散乱，为进一步精确提取直角点，以初始直角点为条件对边界点条件平差，经位置优化后的边界点云再以相邻点夹角为阈值条件，分类直角点.

图4 点相邻向量的夹角关系Fig.4 Angle between two neighbor vectors

筛选出直角点后的特征点有两种可能，圆弧点或一般点，如何识别出圆弧点也是本文重点要解决的问题之一.通过Douglas＿Peucker方法提取出的圆弧特征点应分别位于圆弧的起点、中间点和终点处，所以只要找出圆弧的中间点，圆弧起点终点也能随之明确.

剩余的特征点每相邻3 个一组，对每个特征点相邻两特征点之间的边界点根据圆弧方程

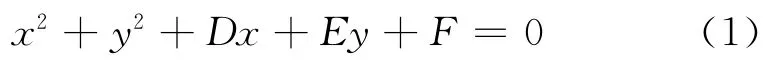
拟合圆弧，其中x，y为拟合点的坐标，D，E，F为圆弧方程的系数，拟合后统计拟合圆弧半径和拟合误差.首先过滤拟合误差过大的特征点，留下拟合误差小于阈值的点；对剩余点的拟合圆弧半径大小进一步过滤，其中拟合圆弧半径小于阈值的点即为圆弧点.若没有符合过滤条件的特征点通过，说明该轮廓线中不包含有圆弧.

其中拟合误差阈值为1.5倍所有拟合点的拟合误差最小值，拟合半径阈值为1.5倍所有拟合点的拟合圆弧半径最小值.

2 轮廓线平差和拟合

LiDAR 系统扫描的建筑物点包含建筑物内部点和边缘点，然而因扫描分辨率限制，点云数据中的建筑物边缘点很难精确处于边缘位置.上述步骤获得的特征点都位于建筑物初步轮廓线形状变化显著的位置，这些特征点已能反映出轮廓线的大致形状，通过进一步的轮廓线拟合能得到更为精确的建筑物形状.对于不同类别的特征点采取不同的方式拟合轮廓线，特征点若为直角点，以该点为交点的两条边界线在此正交，用条件平差方法优化该特征点和其相邻两特征点的位置［13］，使其符合两两垂直的几何关系；特征点若为圆弧点，与其相邻的两特征点即是圆弧的起点和终点，利用起点和终点之间的边界拟合出圆弧作为该处的轮廓线；特征点若为一般点，则不作任何处理.

2.1 轮廓线直线段的平差优化

对于轮廓线中相互垂直的两直线l1和l2，A（Xi，Yi），B（Xj，Yj）是构成直线l1的两个初始房屋角点，B（Xj，Yj），C（Xk，Yk）构成直线l2两个初始房屋角点.若l1和l2两直线满足垂直关系，则构成直线的角点之间满足以下关系：

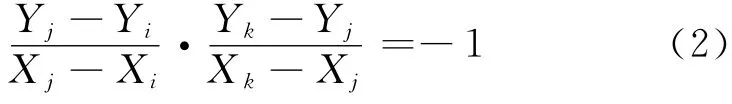
展开上式，以角点坐标的改正值为未知数，用泰勒公式展开，只保留一次项，得到方程的线性化形式，列出如下条件平差的误差方程：

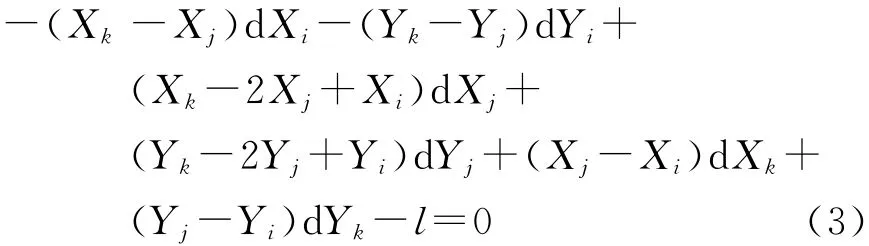
对每对满足垂直关系的相邻直线段的角点列条件方程式（3），得到相互独立的条件方程式组，联立解算得到房屋角点的最优解.

2.2 轮廓线圆弧段的拟合

首先确定属于圆弧的点集，圆弧特征点应位于圆弧线段的中间点，其相邻两特征点就是圆弧的起点和终点，所以起点和终点之间的边界线可被用于拟合圆弧.圆弧线段应符合下式：

将点集中的点X，Y坐标代入式（4），用最小二乘拟合方法求出式（4）中的参数D，E，F，即确定该段位置的圆弧.

3 实验分析

实验数据来源于2007 年采集的上海陆家嘴地区机载LiDAR 数据.陆家嘴地区是上海金融贸易和商业中心，位于上海浦东区，占地约28km2.陆家嘴金融区内建筑物密集，建筑风格各异，形态各异，轮廓线的形状较为复杂，大部分建筑物的轮廓不是简单规则多边形，而是包含有圆弧边界的不规则形状.例如金茂大厦、港务大厦西楼和正大广场等都是轮廓线中含有圆弧线段的复杂建筑物.本文选取陆家嘴地区6幢地标性建筑物的LiDAR 数据作为实验数据，通过本文方法提取建筑物轮廓线与该地区的地形图结果对比，验证本文方法的准确性.

3.1 单幢建筑的轮廓线提取

建筑物轮廓线的提取也就是提取并判断建筑物特征点的过程.首先对建筑物点云构建附带边长比约束的TIN，删除凹角处的三角形得到建筑屋顶内部三角网，如图5所示.在此三角网基础上过滤公共边得到初始边界点.对初始边界点应用Douglas算法，逐次迭代得到轮廓特征点.由特征点计算结果可知，本文方法不仅能检测出多边形转折明显处的点，圆弧上的点也能作为特征点被检测出.根据相邻边界点之间的余弦关系提取出位于直角处的点，在剩余边界点中根据相邻三点拟合的圆弧误差和半径，分类出圆弧点和一般点，分类结果如图6所示.该方法准确分类出不同位置的边界点，与实际情况一致.

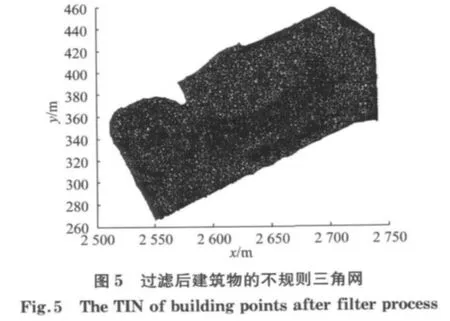
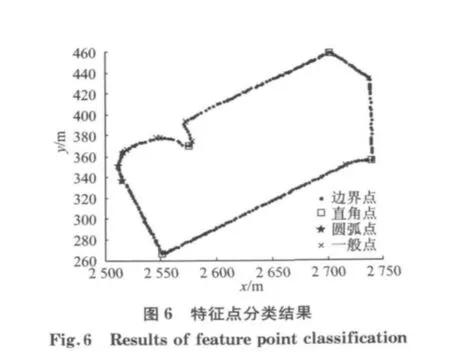
3.2 精度分析

3.2.1 相对精度

以正大广场轮廓线提取结果为例，分析本文方法的提取精度.正大广场的轮廓线共包含14个特征点，其中直角点4个，圆弧点1个，其余的是一般点.直角点处两相互正交的边界线需通过条件平差约束规则化，也就是通过条件平差调整边界线端点处特征点的位置，使边界线满足相互垂直的直角关系.平差后正大广场轮廓线中的特征点单位权中误差为0.040 5m，特征点x，y方向的中误差如表1所示，表中可反映出平差后特征点的点位中误差都在0.04 m 以内.

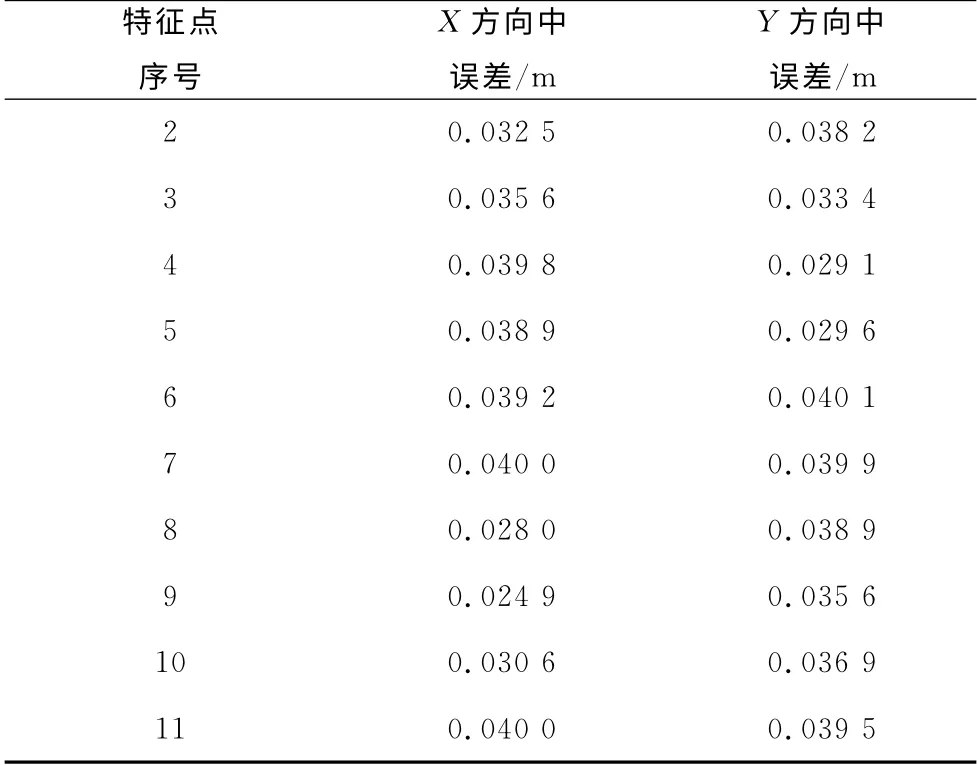
表1 建筑物特征点条件平差优化精度表Tab.1 Accuracy of building feature points condition adjustment

3.2.2 绝对精度

将平差提取的正大广场结果与该建筑1∶500标准地形图数据进行对比，分析平差模型的绝对精度.图7为正大广场平面地形图与提取出的轮廓线的对比图，由图可知本文方法所提取的轮廓线基本吻合建筑物真实轮廓线.

表2为提取出的轮廓线的特征点与真实平面地形图上的特征点的位置距离差异.结合图和表，特征点差异最大的为点3，为2.5m.观察图可知，正大广场该处的LiDAR 点云与真实边界有所差异，LiDAR点云边界不是恰好贴合于建筑物边界，因此从LiDAR 点云中提取得到的特征点跟真实特征点也有所差距.圆弧处特征点跟真实建筑物特征点之间最大差距为0.9m，其余圆弧特征点差距均在1.0m之内.因此，本文方法所提取出的轮廓线可反映出建筑物轮廓线的结构特点，整体上能较好拟合出建筑物的真实形状.

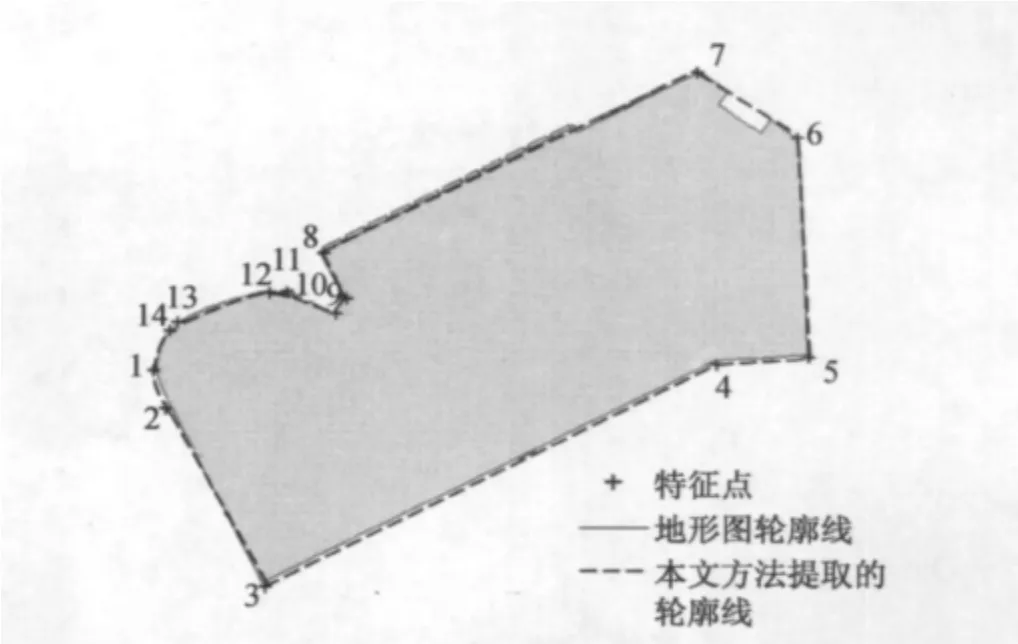
图7 正大广场平面地形图与本文提取的轮廓线对比图Fig.7 Comparison of Zhengda Square’s topographic map and the extracted boundary

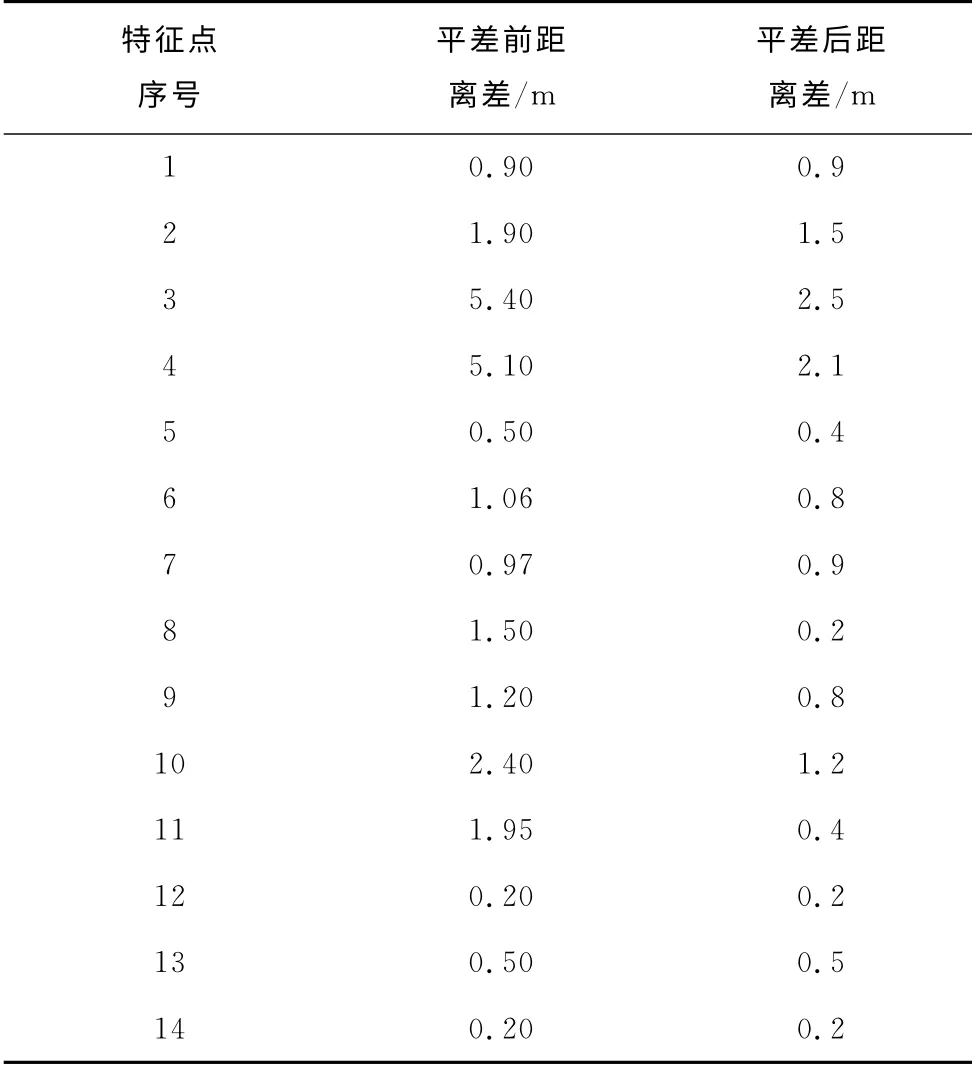
表2 平差前后特征点与地面真实特征点距离差值对比表Tab.2 Difference of distance between feature points in LiDAR and topographic map before and after adjustment

3.3 实验区域的复杂建筑物轮廓提取结果

图8 为陆家嘴地区建筑物平面地形与屋顶LiDAR 点云叠加图.图9表示的是使用本文方法提取的建筑物轮廓线结果.对比图8与图9，本文方法不仅可从LiDAR 点云中提取出规则的简单多边形建筑物轮廓线，例如港务大厦、汇丰银行；对于有圆弧线段的建筑物，本文方法也能有效检测出圆弧点，并拟合优化出符合建筑物真实形状的轮廓线.图9结果表明，本文模型适用于提取多边形或含有圆弧的多种类型的城市复杂建筑物的轮廓.

4 结论

本文着眼于在散乱分布的建筑物LiDAR 点云中精确提取城市中复杂建筑物轮廓线，首先过滤建筑物LiDAR 点云的不规则三角网得到边界点，结合不规则方法筛选得到特征点，并识别特征点属性，判断特征点是直角点、圆弧点或一般点，对直角点出两两垂直的边界线应用条件平差优化特征点的位置，对圆弧点出的边界点采用圆弧拟合方法，最终得到真实的建筑物轮廓线.本文方法不借助于其他遥感图像，也避免将LiDAR 点云内插为图像处理引入的误差，直接基于LiDAR 点云的空间结构关系提取建筑物轮廓线，并且考虑含有圆弧线段的轮廓线.本文方法并不局限于凸多边形建筑物或简单多边形建筑物，可有效地提取出各种形状的复杂建筑物的轮廓线.但是本文方法提取轮廓线依赖于完整提取出建筑物屋顶LiDAR 点云.现阶段机载LiDAR 数据的点间距一般为米级，本文方法受制于LiDAR 数据的空间分辨率、滤波与分类等处理的精度，本算法只针对平面坐标处理，还未考虑高程数据，所以提取建筑物轮廓算法还应进一步改进与研究.

［1］ 何正斌.机载LIDAR 用于数字地面的应用研究［D］.西安：长安大学地质工程与测绘学院，2008.HE Zhengbin.Study of the application on LiDAR for DTM［D］.Xi’an：College of Geology Engineering and Geomatics of Chang’an University，2008.

［2］ 冯琰，郭容寰，程远达.基于机载LiDAR技术快速建立3维城市模型研究［J］.测绘与空间地理信息，2008，31（4）：8.FENG Yan，GUO Ronghuan，CHENG Yuanda.Research on three dimensional city model reconstruction based on airborne LiDAR［J］.Geomatics ＆ Spatial Information Technology.2008，31（4）：8.

［3］ 刘春，陈华云，吴杭彬.激光三维遥感的数据处理与特征提取［M］.北京：科学出版社，2009：84.LIU Chun，CHEN Huayun，WU Hangbin.Process and Feature Extraction of Airborne LIDAR Data Fused with Aerial Image［M］.Beijing：Science Press，2009.84.

［4］ 吴杭彬，刘春.基于数学形态学的LiDAR数据分割和边缘提取［J］.遥感信息，2008（4）：27.WU Hangbin，LIU Chun.Point segmentation and edge detection of LiDAR data based on the mathematical morphology［J］.Remote Sensing Information，2008（4）：27.

［5］ 尤红建，苏林，李树楷.利用机载三维成像仪的DSM 数据自动提取建筑物［J］.武汉大学学报：信息科学版，2002，27（4）：

408.YOU Hongjian，SU Lin，LI Shukai.Automatic extraction of buildings from DSM acquired by airborne three－dimensional imager［J］.Geomatics and Information Science of Wuhan University，2002，27（4）：408.

［6］ Maas H G，Vosselman G.Two Algorithms for extracting building models from raw laser altimetry data ［J］.Photogrammetry and Remote Sensing，1999（54）：153.

［7］ 曾齐红，毛建华，李先华.建筑物LiDAR 点云的屋顶边界提取［J］.武汉大学学报：信息科学版，2009，34（4）：383.ZENG Qihong，MAO Jianhua，LI Xianhua.Building roof boundary extraction from LiDAR point cloud［J］.Geomatics and Information Science of Wuhan University，2009，34（4）：383.

［8］ Lach R S，Kerekes P J.Robust extraction of exterior building boundaries from topographic LiDAR Data ［C］∥IEEE International，Geoscience and Remote Sensing Symposium.［S.l.］：IEEE，2008：85－88.

［9］ 沈蔚，李京，陈云浩.基于LiDAR数据的建筑物轮廓线提取及规则化算法研究［J］.遥感学报，2008，12（5）：692.SHEN Wei，LI Jing，CHEN Yunhao.Algorithms study of building boundary extraction and normalization based on LIDAR data［J］.Journal of Remote Sensing，2008，12（5）：692.

［10］ Sampath A， Shan J. Building boundary tracing and regularization from airborne lidar point clouds［J］.Journal Remote Sensing，2007（7）：805.

［11］ 张真.一种改进的基于Douglas－Peucker原理的轮廓采样算法［J］.电脑知识与技术，2009（25）：7214.ZHANG Zhen.An improved contour sampling algorithm based on Douglas－Peucker theory［J］.Computer Knowledge and Technologh，2009（25）：7214.

［12］ Wang J Y，Zhang C M，Yang X Q，et al.Segmentation from stratified range image［J］.Journal of Software，2003（4）：790.

［13］ 阎平.LIDAR数据中多层次、多直角房屋的三维重建［D］.武汉：武汉大学测绘遥感信息工程国家重点实验室，2005.YAN Ping.Reconstruction of buildings with multi right angles and multilayers from LiDAR［D］.Wuhan：State Key Laboratory of Information Engineering in Surveying，Mapping and Remote Sensing of Wuhan University，2005.