单频非差相位观测值的周跳探测与修复方法
2012-12-03王解先
王 成,王解先
(同济大学 测绘与地理信息学院,上海200092)
在高精度GPS(global positioning system)数据处理中,周跳探测一直是GPS载波相位观测数据预处理中比较重要的问题.周跳的探测与修复对于后续模糊度的确定以及最终定位结果的精度至关重要.针对相关内容,国内外学者做了一系列研究,目前常用的周跳探测方法有:多项式拟合法、高次差法、双频码相组合法、电离层残差法以及各种星间或站间差分方法等[1-2].其中比较有效的周跳探测方法如电离层残差法、MW(Melbourne-Wübbena)组合探测法等都是基于双频观测数据的,而单频接收机数据无法构成MW 组合以及电离层残差组合,因此周跳的探测与修复是单频精密单点定位技术的难点之一.非差相位观测值的周跳探测方法相比双差模式的少,而单频非差相位观测值的周跳探测则更加困难,一些经典的周跳探测方法对于单频非差相位观测值的周跳探测不再适用.针对这一问题,国内一些学者提出了相应的处理方法.2001年,贾沛璋采用3阶多项式模型的卡尔曼滤波检测周跳,该方法适用于采样率为1Hz的观测数据[3].2009年,曹佚之提出基于信息向量的自适应两步阶段卡尔曼滤波,克服了滤波容易发散的特点,对于高采样率的单频GPS周跳探测与修复具有良好的效果,但随着采样间隔加大,该方法周跳探测能力随之下降[4].2010年,陶庭叶采用一类支持向量机可有效探测静态或低动态情况下的周跳,但核函数及其参数的选择对于周跳探测准确率有较大影响,如何合理选择模型参数需要进一步研究[5].2011年,腾云龙将时间序列分析用于周跳探测与修复,该方法由于采用的差分次数较多,对于1~3周的小周跳,差分序列跳变幅度不明显从而难以准确判定是否发生周跳[6].传统的多项式拟合和高次差分法对采样率要求较高,且难以探测小周跳[2].在低采样率下,利用多普勒观测值计算的相位变化无法反应历元间观测值的实际变化,从而影响周跳探测的可靠性[7].本文对伪距与载波相位观测值做二次差分进而构造周跳检验量,并基于灰色理论对周跳检验量进行预测,然后判定下一历元的周跳检验量是否在预测的数值区间内,如果在预测范围内,则认为观测数据正常,否则认为发生周跳.试验结果表明,该方法简单易行,不仅能有效适用于不同采样率数据的周跳探测,还可对载波相位值进行修复,为单频非差精密单点定位提供了良好的数据质量控制.
1 周跳探测的数学模型
1.1 周跳检验量的构造
伪距观测方程与载波相位观测方程分别为
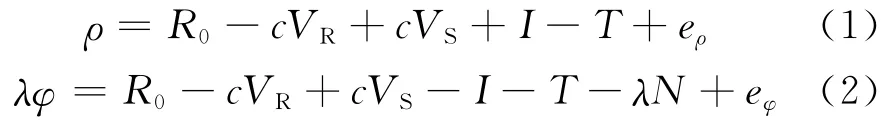
式中:ρ为伪距观测值;R0为站星几何距离;c为光速;VR为接收机钟差;VS为卫星钟差;I为电离层延迟量;T为对流层延迟量;eρ为包含多路径效应影响与伪距观测噪声等综合误差;λ为载波波长;N为整周模糊度;eφ为包含多路径效应影响与载波相位噪声等综合误差.
将式(1)与式(2)作差,消去了站星几何距离、接收机钟差、卫星钟差和对流层延迟量得
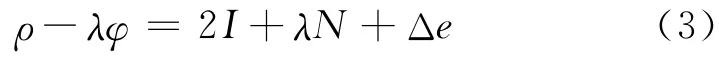
将式(3)在历元间作差,可消去整周模糊度这一项,得
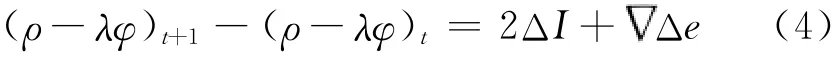
式中:ΔI为电离层延迟量的变化量;Δe为差分综合误差.
假设第t+1历元发生周跳,设周跳参数为v,则
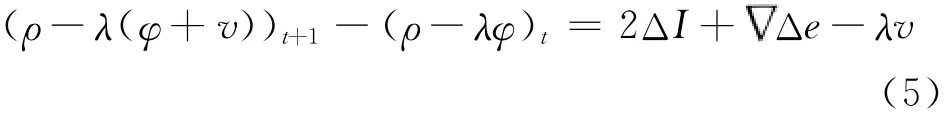
将式(5)两边同时除以波长λ,得
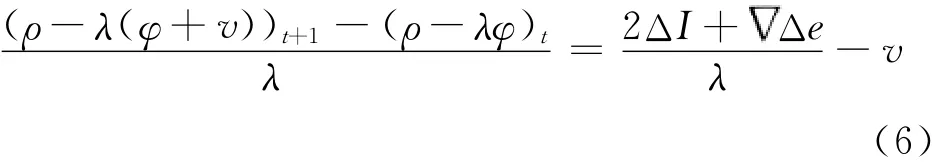
根据式(6)构造周跳检验量为
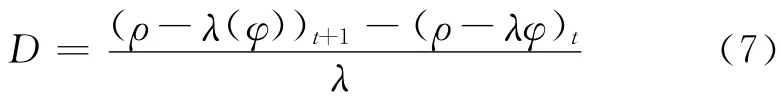
由式(6)和式(7)可知,如果电离层延迟量的变化量和差分综合误差在时间序列上表现为平滑的特性,即可使用式(7)的周跳检验量来探测周跳.
1.2 周跳检验量的时间序列
一般来说,如果没有发生周跳,由式(7)构造的周跳检验量在时间序列上表现为相对平滑的曲线,如图1;若发生周跳时,这种平滑的特性将被破坏进而使周跳检验量在时序上发生突变,如图2.
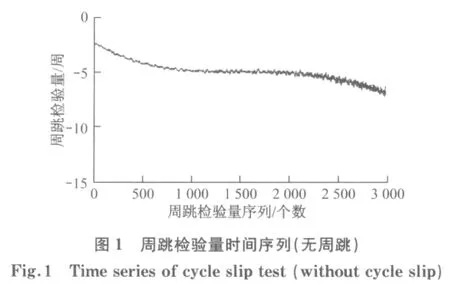
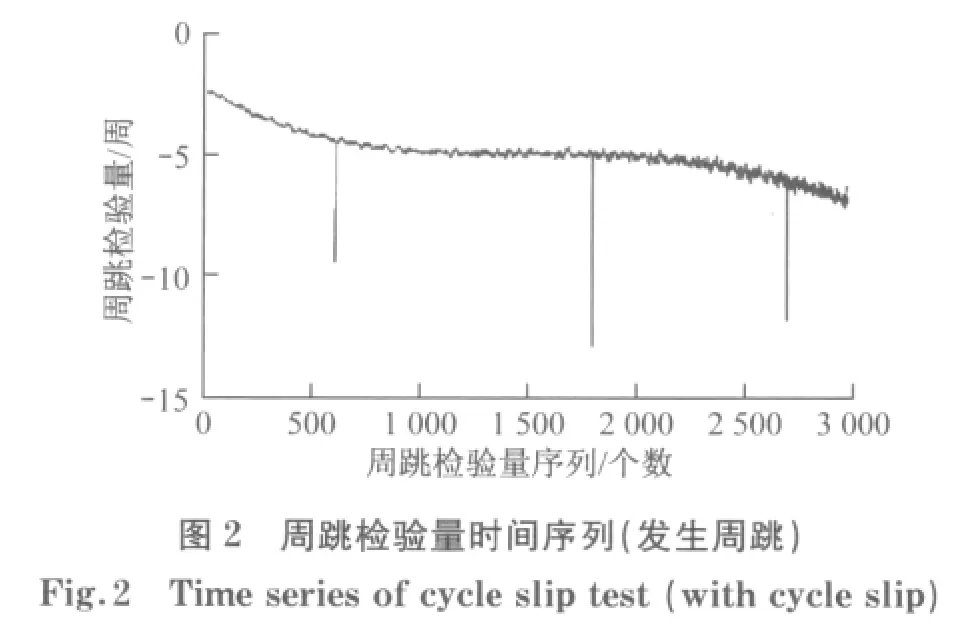
由图1和图2可知,如果没有发生周跳,周跳检验量在短时段内变化不大,在时序上比较平缓,一旦发生周跳,则会破坏原有的平滑特征.
1.3 灰色预测
灰色系统理论把一切随机过程看作是在一定范围内变化的、与时间有关的灰色过程,用数据生成的方法,将杂乱无章的原始数据整理成规律性较强的生成数列后再作研究.累加生成与累减生成是灰色系统理论与方法中的两种数据生成方法,常用于建模[8].设原始数列为
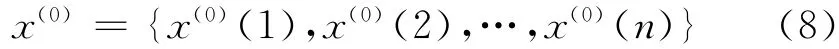
对x(0)作一次累加生成
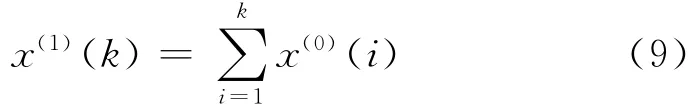
即可得到一个生成序列
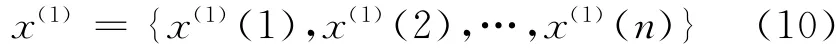
对此生成序列建立1阶微分方程
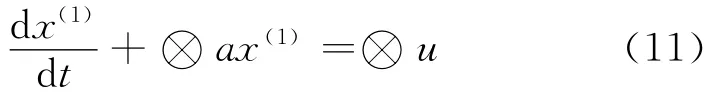
式中,⊗a和⊗u是灰参数,其白化值为a^=[au]T.用最小二乘法求解,得
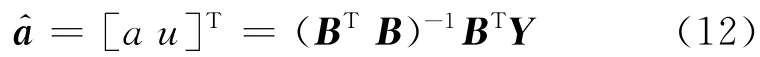
式中:
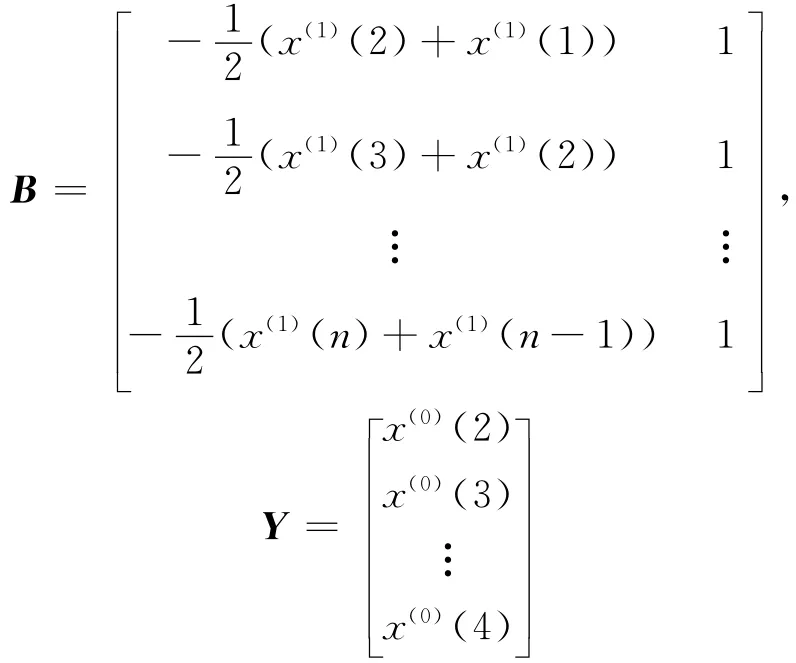
求得a^后带入式(11),解微分方程得
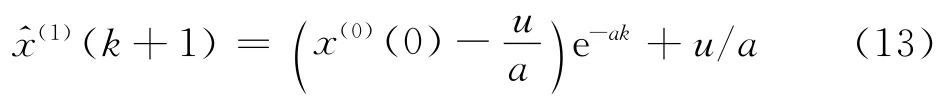
对x^(1)(k+1)作累减生成,可还原数据
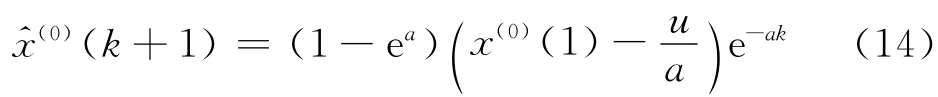
当k<n时,称x^(0)(k)为模型模拟值;当k=n时,称x^(0)(k)为模型滤波值;当k>n时,称x^(0)(k)为模型预测值.
对于模型精度即模型拟合程度评定的方法有残差大小检验、关联度检验和后验差检验3种.其中残差大小检验是对模型值和实际值的误差进行逐点检验;关联度检验是考察模型值与建模序列曲线的相似程度;后验差检验是对残差分布的统计特性进行检验[9-10].本文采用残差大小检验方法来检验周跳检验量预测值与实测值的符合接近程度.灰预测包含数列灰预测、灾变灰预测、季节灾变灰预测、拓扑灰预测和系统灰预测[8].本文根据周跳检验量的时序特征选择数列灰预测方法.
2 周跳探测与修复
利用灰色理论建模的主要目的是预测,但随着预报步数的增加,预报准确性越差,所以预报的步数应尽可能小.为了提高预测的精度和可靠性,本文选择由若干历元(一般取10~30)周跳检验量构成灰色理论的原始数列窗口,对窗口内的数据进行灰色建模并计算灰色预测值与预测区间,之后对实测值进行检验,具体步骤如下:
(1)对当前历元窗口内的周跳检验量进行灰色建模计算预测值,并与窗口内周跳检验量的3倍中误差构成预测区间;
(2)判定历元窗口之后的下一个历元周跳检验量是否在预测区间内,如果在范围内则表明没有发生周跳,否则认为发生周跳;
(3)如果发生周跳,需要对该历元进行周跳修复,即用预测值减去该历元周跳检验值四舍五入取整,然后对该历元及后续所有相位观测值减去这个数值;
(4)加入一个最新历元的周跳检验量,去掉一个最旧历元的周跳检验量,构造新的历元窗口,重复上述步骤,依次进行周跳探测与修复.
周跳探测与修复的流程图见图3.

图3 周跳探测流程图Fig.3 Flow diagram of cycle slip detection
3 实验分析
采 用2009 年5 月10 日 某 测 站GPS 观 测 数 据26号卫星一个弧段的干净数据,历元窗口选择为10,使用上述周跳探测方法分别对以下3种方案进行算例分析,各方案周跳检验量及残差如图4—9,周跳探测及修复信息如表1.
(1)采样间隔为5s,对载波在第800,1 800,2 700历元分别加入1周、8周和6周;
(2)采样间隔为15s,对载波在第300,550,700历元分别加入10周、1周和8周;
(3)采用间隔为30s,对载波在第100,230,400历元分别加入25周、10周和3周.
由图4—9及表1可知,在高采样率下,灰色模型的建模精度较高,预测值与实际周跳检验量的符合程度较好,当发生周跳时,实测周跳检验量会超出预测范围进而探测出周跳,同时将预测值与实测值
作差即可得到周跳改正量,从而实现周跳的快速修复.当采样间隔增大到30s时,建模精度有所下降,预测值与实际周跳检验量的符合程度降低,历元窗口内的周跳检验量的方差增大,从而使预测区间增大,导致不能探测小于3周左右的周跳,并且周跳修复存在1周左右的偏差.
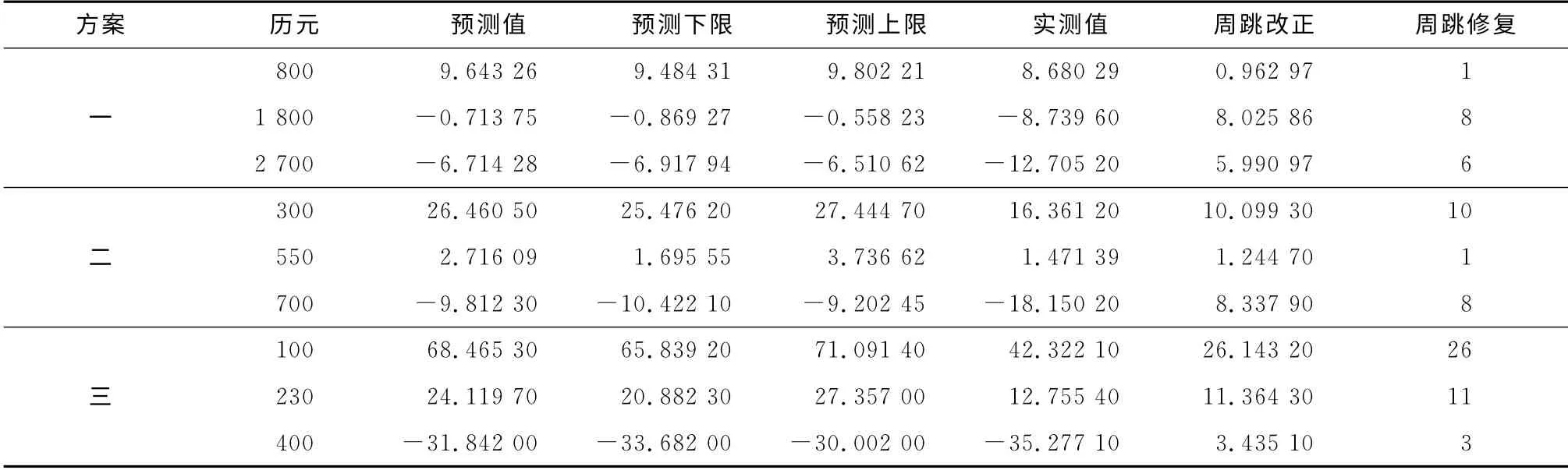
表1 各方案周跳探测与修复信息Tab.1 Slip detection and correction information of different projects 周
此外,当卫星高度角邻近最大时,卫星相对于测站的运动趋势有所变化,周跳检验量由正到负,此时建模精度较差.根据灰理论中的级比判断准则也可验证方案一中的周跳检验量序列不具备GM(1,1)建模的可行性[8].为此,可将方案一周跳检验量序列的每一个值分别减去序列最小值从而得到一组非负的序列,然后用灰理论建模得到模型值,最后加上原序列最小值即可.另外,可采用内生控制灰数u近似作为预测值,如果事后处理,可在高度角邻近最大前后分别建模.采用26号卫星的一段数据,采样间隔为30s,历元窗口为10,最大高度角位于314历元,分别对以下4种方案进行算例分析:①历元窗口为285至294,位于邻近最大高度角;②历元窗口为251至260,位于最大高度角前;③历元窗口为315至324,位于最大高度角后;④数据同方案一,采用改进灰色模型.其中卫星高度角如图10,周跳检验量样本如图11,残差如图12,相关计算结果如表2.
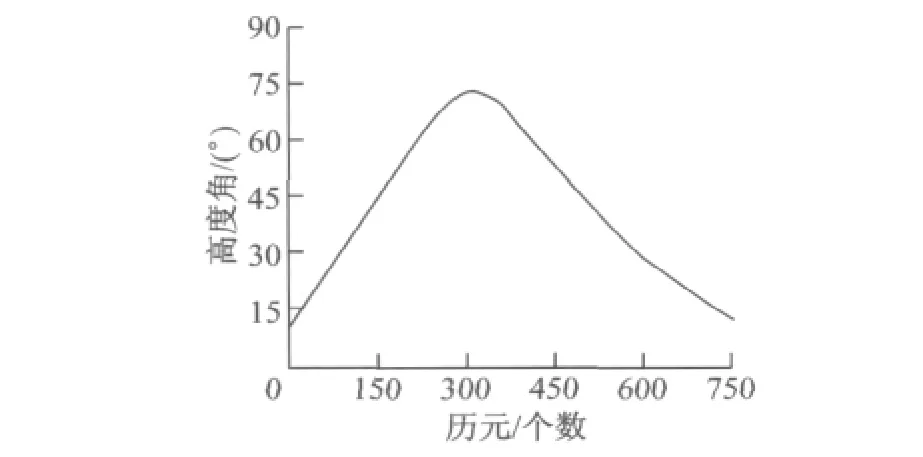
图10 卫星高度角Fig.10 Altitude angle of satellite
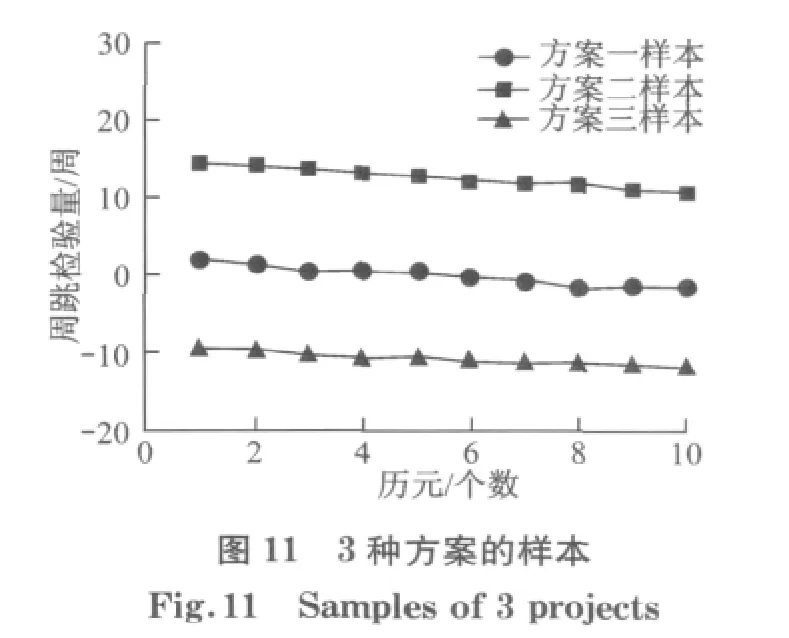
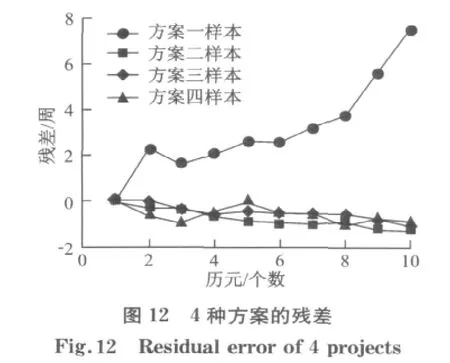
由图11,12及表2可知当周跳检验量序列的数值都为正数或负数时,GM(1,1)模型的建模精度较好,而同时包含正数和负数的方案一建模精度较差.表2中方案一的第2行为预测值采用内生控制灰数的相关信息,可知当数据序列不具备建立GM(1,1)模型时也可近似采用内生控制灰数作为预测值,但却违背了灰理论建模的条件,而改进的灰色模型不仅能够符合灰建模的条件,其建模精度和通常的序列建模精度基本一致,能够有效用于周跳探测.

表2 4种方案周跳探测信息Tab.2 Slip detection information of 4projects 周
4 结语
本文使用单频单测站的伪距与载波相位观测值构造周跳检验量,采用灰色理论对历元窗口内周跳检验量进行建模计算预测值以及预测区间,通过检验实测周跳检验量是否落在预测范围内来判断是否发生周跳.通过算例分析表明,该方法计算简单,易于实现,对于5s,15s采样间隔的非差载波相位观测值能够有效地探测1周及以上的周跳,并且能够较好地修复周跳,对于30s采样间隔的数据能够探测3周及以上的周跳,但周跳修复存在1周左右的偏差.当卫星高度角不断增大,电离层延迟量的变化量和差分综合误差历元间差分出现负值,此时建模精度较差,当周跳检验量序列中同时含有正负数时,不具备灰色建模的可行性,而采用改进灰色模型先将序列编辑为非负数从而能够符合灰建模的条件,然后建模得到模型值及预测值,并能够用于周跳探测.由于本文实验所采用的单频数据是从双频接收机所接收数据中提取的单个频率的观测值,而一般情况下单频接收机所获取的数据质量通常比双频接收机的差,因此,在实际应用中,使用单频非差载波相位观测值进行周跳探测时,其精度水平可能低于上述精度指标.
[1] 李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.LI Zhenghang,ZHANG Xiaohong.New techniques and trecise data processing methods of satellite navigation and positioning[M].Wuhan:Wuhan University Press,2009.
[2] WANG Tiesheng,ZHANG Bing,LI Shanshan.The research of the cycle slips’detection method in GPS navigation and positioning[C]∥International Conference on Optoelectronics and Image Processing,Haikou:[s.n.]2010,609-611.
[3] 贾沛璋,吴连大.单频GPS周跳检测与估计算法[J].天文学报,2001,42(2):192.JIA Peizhang,WU Lianda.An algorithm of detecting and estimating cycle slips single frequency GPS [J]. Acta Astronomica Sinica,2001,42(2):192.
[4] 曹佚之,隋立芬,王威.一种单频GPS周跳探测的自适应滤波算法[J].大地测量与地球动力学,2009,29(4):83.CAO Yizhi,SUI Lifen,Wang Wei.Detecting cycle slips in GPS single frequency carrier phase using an adaptive filter[J].Journal of Geodesy and Geodynamics,2009,29(4):83.
[5] 陶庭叶,高飞,吴兆福.利用一类支持向量机探测GPS载波相位的周跳[J].大地测量与地球动力学,2010,30(1):119.TAO Tingye,GAO Fei,WU Zhaofu.Detecting cycle slips in GPS carrier phase by using one class support vector machine[J].Journal of Geodesy and Geodynamics,2010,30(1):119.
[6] 腾云龙,师奕兵,郑植.时间序列分析在周跳探测与修复中的应用[J].宇航学报,2011,32(3):543.TENG Yunlong,SHI Yibing,ZHENG Zhi.Time series analysis and its application in detection and correction of cycle slip[J].Journal of Astronautics,2011,32(3):543.
[7] 张小红,李星星,郭斐,等.GPS单频精密单点定位软件实现与精度分析[J].武汉大学学报:信息科学版,2008,33(8):783.ZHANG Xiaohong,LI Xingxing,Guo Fei,et al.Realization and precision analysis of single-frequency precise point positioning software[J].Geomatics and Information Science of Wuhan Universiy,2008,33(8):783.
[8] 邓聚龙.灰理论基础[M].武汉:华中科技大学出版社,2002.DENG Julong.Grey theory basis[M].Wuhan:Huazhong University of Science and Technology Press,2002.
[9] 黄声亨,尹晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010.HUANG Shengheng,YING Hui,JIANG Zheng.Deformation monitoring data processing[M].Wuhan:Wuhan University Press,2010.
[10] XU Guoxiang.Statistical forecasts and decision making[EB/OL].http://course.shufe.edu.cn/course/tjyc/multimedia/10.ppt,2005.
