电沉积镍涂层的冲压成形极限右边分析与预测

周里群 李玉平 龙文宝

1.湖南工程学院，湘潭，411105 2.湘潭大学，湘潭，411105

0 引言

电沉积镍涂层具有良好的耐磨性、装饰性和防腐性，在工程上得到了广泛应用［1－2］，但电沉积镍涂层用于零部件的冲压成形还是一个值得研究与探讨的课题［3］。现代电池钢壳的生产工艺是：先将镍涂层沉积于低碳钢薄板上，然后对涂层薄板冲压成形，故涂层薄板的冲压成形性能非常关键［4］。涂层薄板在冲压成形过程中，涂层一般与模具直接接触，而涂层的力学性能与塑性又低于低碳钢基体，因此涂层薄板的成形性能在很大程度上取决于涂层。因此需要对涂层的制备及涂层的冲压成形性能开展研究。

1 涂层薄板的等效应力与等效应变增量

笔者运用Hill的正交各向异性塑性理论推导了涂层薄板在冲压过程中的等效应力和等效应变增量。涂层薄板第i层的等效应力与1轴主应力的关系为［3］

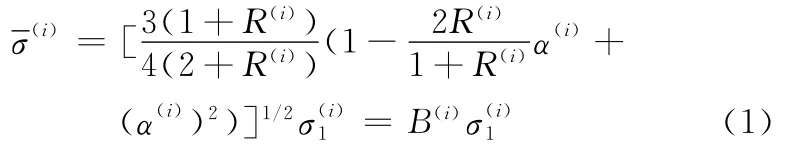
式中，R（i）为第i层材料的厚向异性指数；α（i）为第i层的应力比。

式（1）表明，涂层薄板在变形过程中各层的等效应力不同。

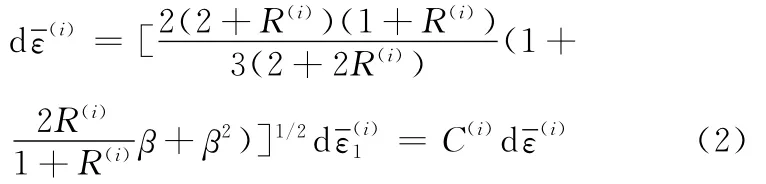
式中，β为单层的应变比。

式（2）表明，涂层薄板在变形过程中，各层的等效应变不同。

假定涂层薄板接合面的主应变相等，因此对涂层薄板的第i层有

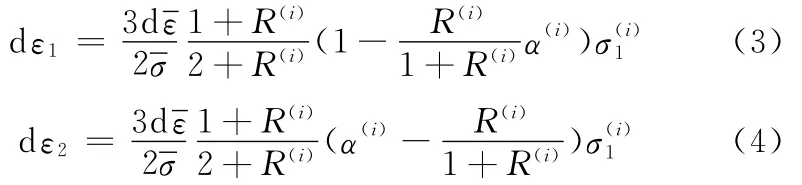
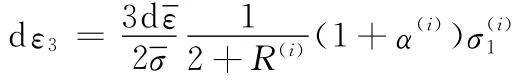
由式（3）、式（4）可得单层的应变比β：

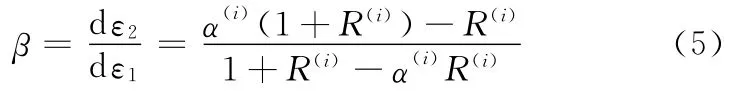
计算成形极限时，给定β的变化值，则第i层的应力比为

其中，R（i）由实验测定。由式（6）可知，涂层薄板各层的厚向异向指数不同，涂层薄板在变形过程中各层的应力比不同。

2 涂层薄板的应力应变数据拟合

在实验室制备了镍涂层钢带，涂层分布在基体两侧，厚度可控。作为基体的低碳钢钢带的厚度为0.25mm。冲击实验结果显示，涂层和基体在接合面上具有良好的结合［5］。

在改进的扫描电镜上进行实验，测得了镍涂层及低碳钢基体的应力应变数据，然后采用最小二乘法对数据拟合成Hollomon方程：对于镍涂层，σ＝1805.6ε0.3570MPa；对 于 钢 带 基 体，σ＝946.3ε0.3696MPa［6］。

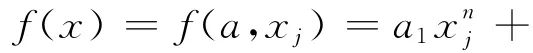
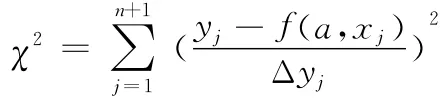
模型多项式的阶次取得太低，拟合就粗糙，阶次太高，拟合就会“过头”，使数据噪声也被纳入模型。本文通过计算从1阶到6阶（n＝1，2，…，6）的Q值来合理选择拟合阶次：

Q（χ2，N－（n＋1））＝1－P（χ2＜ （N－n－1））

P（χ2＜（N－n－1））利用分布的累计概率指令chi2cdf（chi2，（N－n－1））算出，用5次多项式拟合就能得到好的逼近效果，即

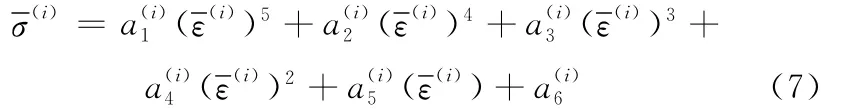
经过计算可得各系数的值，如表1所示。多项式拟合曲线与测试数据有很好的逼近［8］。

表1 拟合多项式系数

3 电沉积镍涂层成形极限右边曲线的推导

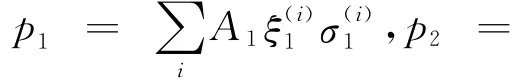
式中，C为常数。

根据Swift分散颈缩条件，即载荷的极值为零，可以求得

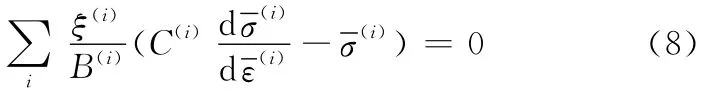
4 计算结果与分析

图3所示为涂层薄板的成形极限曲线，其中镍涂层厚度为5μm，钢基体厚度为0.25mm，n′为材料应变硬化指数，涂层钢带基体厚向异性指数为1.41［11］。由图3中的曲线2和曲线3可见，镍涂层的成形极限没有低碳钢基体的那么高。图3中，曲线1为按多项式拟合的涂层薄板成形极限曲线，曲线4为按传统方法采用Hollomon拟合得到的成形极限曲线，可见两者的成形极限区域相差较大，采用实际应力应变曲线多项式拟合的成形极限小很多。说明采用实际应力应变的多项式拟合计算具有良好的意义。

图4和图5所示为基体和涂层的厚向异性指数对涂层钢带成形极限的影响。由图4（R（3）为基体的厚向异性指数，涂层视为各向同性体）可以看出，基体厚向异性指数越大，成形极限曲线就越高，而且影响很显著。图5（R（1）为涂层的厚向异性指数，R（3）＝1.41）中，涂层厚向异性指数对成形极限的影响不是很显著，可能是由于涂层很薄的缘故。由此可见，厚向异性指数小于1对成形不利，增大基体的厚向异性指数能提高成形极限。这与文献［12］中的研究结果是一致的。

图6（涂层视为各向同性体，R（3）＝1.41）所示为镍涂层厚度t对涂层钢带成形极限的影响。由图6可知，当低碳钢基体的厚度不变时，减小镍涂层的厚度，涂层薄板的成形极限曲线将提高。这是因为镍涂层的成形极限没有钢基体的那么好，当复合板组分材料中成形性能好的材料的厚比增大时，复合板的成形极限将提高［10］。这表明在允许范围内，减小涂层厚度能提高涂层薄板的成形极限。减小涂层厚度也可以降低材料制备成本，因此具有实际意义。

5 结论

（1）基于实际应力应变曲线运用多项式拟合计算得到的涂层薄板的成形极限低于Hollomom公式计算出的成形极限。

（2）涂层厚度、基体厚向异性指数对涂层薄板的成形极限有显著影响，而涂层厚向异性指数对成形极限没有显著影响。

（3）镍涂层的成形性能低于低碳钢基体的成形性能。参考文献：

［1］Nicolas S，Evangelia A P，Styliani S，et al.Nickel and Nickel－phosphorous Matrix Composite Electrocoatings［J］.Transactions of Nonferrous Metals Society of China，2009，19（4）：800－804.

［2］Zhou Zhaofeng，Pan Yong，Lei Weixin.Ni Nanocomposite Films Formed by Ni Nanowires Embedded in Ni Matrix Using Electrodeposition［J］.Transactions of Nonferrous Metals Society of China，2010，20（4）：637－642.

［3］周里群.电沉积镍涂层的冲压性能与冲压成形过程分析［D］.湘潭：湘潭大学，2004.

［4］Zhou L Q，Li Y P，Zhou Y Q.Numerical Analysis of Electrodeposited Nickel Coating in Multisting Drawing Processes［J］.Journal of Engineering Materials and Technology，2005，127（4）：233－243.

［5］Zhou L Q，Zhou Y C，Pan Y.Impact Performance of Electrodeposited Nickel Coating on Steel Substrate［J］.Journal of Materials Science，2004，39（2）：753－755.

［6］Zhou Liqun，Li Yuping，Zhou Yichun.Study on Forming Limits of Nickel Coating on Right Region［J］.Transactions of Nonferrous Metals Society of China，2007，17（5）：913－918.

［7］张志涌.精通 MATLAB［M］.北京：北京航天航空大学出版社，2000.

［8］Zhou Liqun，Tang Jianguo，Li Yuping，et al.Working Performance of Electrodeposited Nickel Coating［C］／／International Conference on Mechanical Engi－neering and Mechanics.Wuxi，China，2007：1750－1756.

［9］肖景容，江奎华.冲压工艺学［M］.北京：机械工业出版社，2000.

［10］彭志辉，佘旭凡.不锈钢覆铝板成形极限的理论分析和实验验证［J］.中国有色金属学报，1999，9（2）：305－312.

［11］Zhou L Q，Li Y P，Zhou Y C.Forming Limit of Electrodeposited Nickel Coating in the Left Region［J］.Journal of Materials Engineering and Performance，2006，15（3）：287－294.

［12］Wan M，Yang Y Y，Li S B.Determination of Fracture Criteria during the Deep Drawing of Conical Cups［J］.Journal of Materials Processing Technology，2001，114（1／3）：109－113.