含沟槽结构的水润滑橡胶轴承三维弹流润滑分析

刘文红，王家序，周广武，吴 松

(1.重庆大学机械传动国家重点实验室，重庆400044;2.中国工程物理研究院化工材料研究所，四川绵阳621900)

0 引言

弹流润滑(EHL)是一种流体薄膜润滑方式.与传统的油润滑金属滑动轴承不同，水润滑轴承刚度较小且容易发生变形，并且具有多曲面、多纵向凹槽的几何结构，这对水润滑轴承的润滑性能产生显著影响.Pai等［1］利用CFD软件模拟了三轴向凹槽的水润滑轴承流体流动，得到了水膜压力分布.Majumdar等［2］采用了更接近实际工况的边界条件，分析了三纵向沟槽水润滑轴承的稳态性和动态特性，研究表明水润滑轴承水膜最大压力并不是出现在轴承的中部，而是沿轴向逐步下降.Tanamal等［3］利用CFD软件分析了不同沟槽数量、布置方式以及润滑剂种类对水润滑轴承的润滑特性和承载能力的影响.Pai等［4］研究了动载荷对四轴向凹槽和六轴向凹槽的水润滑轴承运行稳定性的影响.上述文献均未考虑水润滑轴承的弹性变形对润滑性能的影响.Alex等［5］对有限长弹性径向滑动轴承进行混合润滑研究，得到了水润滑轴承的Stribeck曲线.但是该文献没有考虑水润滑橡胶轴承的凹槽几何结构.Cabrera等［6］通过实验和CFD分析了水润滑橡胶轴承内的压力分布以及橡胶变形，结果表明水润滑橡胶轴承内的压力分布与一般硬质表面轴承内的压力分布有很大的差异，即使在较低压力下，橡胶也易产生变形，并且水的黏度随压力变形不明显.卢磊等［7］利用ANSYS的流固耦合功能对六沟槽水润滑橡胶合金轴承进行2D数值模拟.王家序等［8］利用ADINA流固耦合求解器对平面板条式水润滑橡胶合金轴承在中低速条件下的润滑性能进行2D数值仿真.然而，文献［6-8］没有根据水润滑轴承实际工况，分析水润滑橡胶合金轴承三维弹流润滑特性.

因此，笔者综合考虑水润滑橡胶合金轴承的橡胶弹性变形以及多曲面、多纵向凹槽的几何结构，利用有限元ANSYSCFX软件分析水润滑橡胶合金轴承三维紊流状态下的弹流润滑特性，研究不同偏心率、转速对水润滑橡胶合金轴承的水膜压力分布、水膜厚度分布、承载能力以及摩擦系数的影响.

1 控制方程的建立

1.1 计算模型

水润滑橡胶合金轴承示意图，如图1所示.

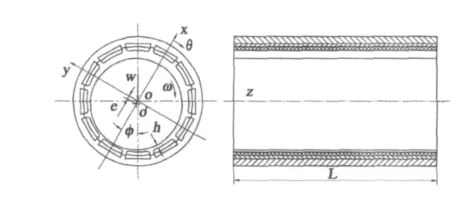
图1 水润滑橡胶合金轴承示意图Fig.1 Diagram of water-lubricated rubber bearing

分析中所用水润滑橡胶合金轴承几何与材料参数见表1.

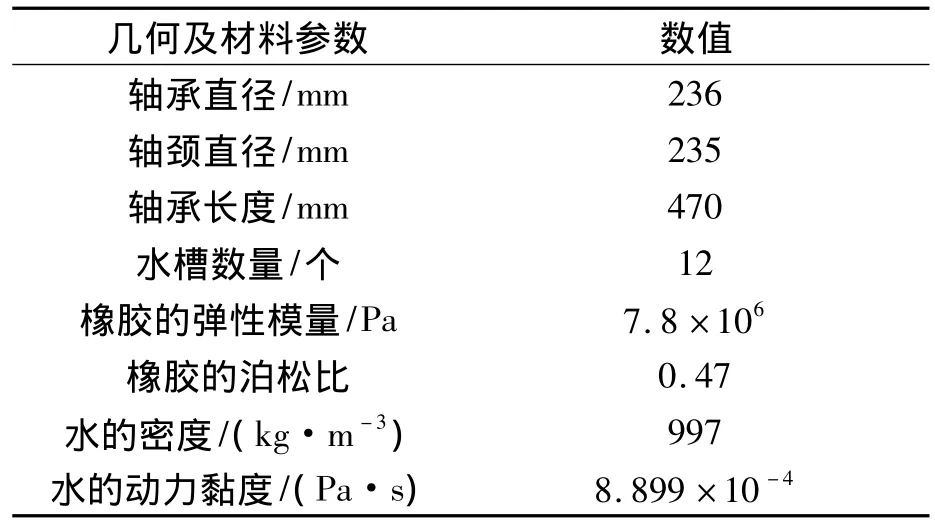
表1 水润滑橡胶合金轴承几何和材料参数Tab.1 Geometric and material of water-lubricated rubber bearing

1.2 假设条件

①水的黏度较低，水膜压力较小，忽略黏压效应;②假设水为不可压缩流体，忽略密压效应;③多纵向凹槽的几何结构有利于散热，忽略温黏效应;④由于橡胶亲水性好，水又是黏性液体，认为水介质在轴颈和橡胶衬层表面满足无滑移条件;⑤忽略橡胶吸水膨胀;⑥考虑水润滑轴承的凹槽结构，水进入楔形收敛域时部分水回流至沟槽形成漩涡，故假设水的流动为紊流.

1.3 控制方程

(1)质量守恒方程即连续性方程:

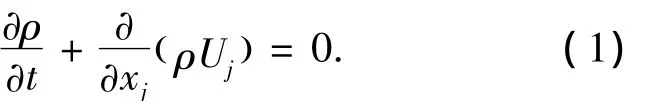
(2)动量守恒方程即Navier-Stokes方程:

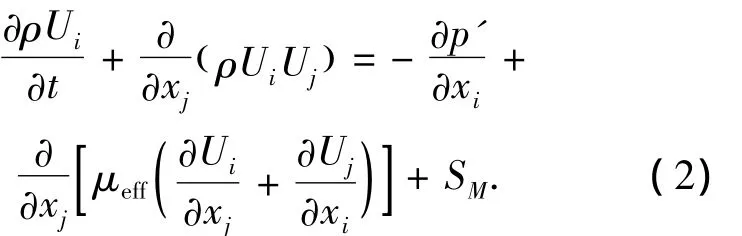
式中:μeff=μ+μt;SM为体积力;p'为修正压力;μeff为等效黏性系数;μ为分子黏性系数;μt为紊动黏性系数.

(3)水膜厚度方程.由于水润滑橡胶合金轴承具有多曲面、多纵向凹槽的几何结构，以及在承载时易发生弹性变形，故在径向截面的水膜厚度方程包含刚性间隙和橡胶的弹性变形，其表达式为:

式中:c是轴承半径间隙;ε是偏心率(ε=e/c);h0x，y，()z为凹槽的深度;δx，y，()z是橡胶衬层的径向弹性变形.

(4)承载能力和偏位角.得到水膜压力分布后，利用下式计算承载能力w和偏位角φ:

(5)摩擦力和摩擦系数.摩擦力f通过轴颈上沿周向对剪切力积分:

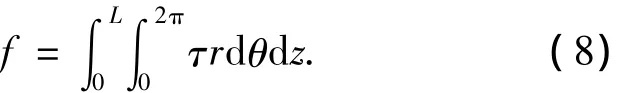
摩擦系数:

笔者采用剪切应力输运(SST)湍流模型.

2 有限元模型

2.1 流固耦合求解

水润滑橡胶合金轴承的弹流润滑实质就是流体动压润滑与结构弹性变形之间的双向流固耦合过程.在润滑过程中，水膜压力作用到橡胶衬层上，使之发生弹性变形，而橡胶弹性变形反过来又改变水膜厚度，进而影响水膜压力分布.采用ANSYSCFX中的多场耦合代码求解器(MFX)进行求解.

2.2 边界条件

考虑到轴为刚性材料，相对于水膜和橡胶的变形极小，因此忽略轴的弹性变形对水膜的影响.将轴与水膜的接触面假设为无滑移壁面条件，其旋转边界条件为轴的转速.橡胶衬层与水膜接触面设定为双向流固耦合边界.轴承外表面设定为固定约束.对于开式水润滑轴承系统，由水泵供水，其供水压力通常为70～100 kPa，而螺旋桨处于水下2 m处，其出口压力约为20 kPa.故z=0处，设定入口压力为90 kPa;z=L处，设定出口压力为20 kPa.

3 计算结果与讨论

3.1 水膜压力分布

3.1.1 转速对水膜压力分布的影响

图2给出了偏心率为0.6，转速分别为100，500，1 000 r/min时的水膜压力分布云图.可以看出，随着转速的增大，流体动压效应越明显，压力沿圆周方向变化越来越明显，最大压力峰值越大.当转速为100 r/min时，最大压力峰值为90.65 kPa，略高于入口压力;当转速为1 000 r/min时，最大压力峰值为158.3 kPa，为入口压力的1.75倍.由于外界压力和多沟槽效应以及橡胶弹性变形对水膜压力分布的影响，在轴承入口和中截面均未出现Sommerfeld边界条件下的负压力.但是，在出口处出现了负压力，显然这种负压力是不合理的，因为在负压情况下水膜会发生破裂.究其原因是计算流体软件所采用的边界条件为Sommerfeld边界条件.考虑到负压只出现在轴承出口小部分区域，它对整个轴承的弹流分析影响甚小，因此忽略负压的影响［3］.

图2 不同转速下的水膜压力分布Fig.2 Water film pressure distribution in different rotate speed

3.1.2 不同截面水膜压力分布对比

图3给出了偏心率为0.6，转速为1 000 r/min时，轴承入口处、中截面和出口处周向水膜压力分布曲线.曲线表明不同截面上水膜压力均出现12个压力峰值，这是由于轴承12根板条和12个凹槽的几何结构所形成的12个楔形区域所致.由于轴颈旋转产生流体动压效应和进出口压力差，轴向截面上的最大压力峰值依次顺延，且逐渐降低.

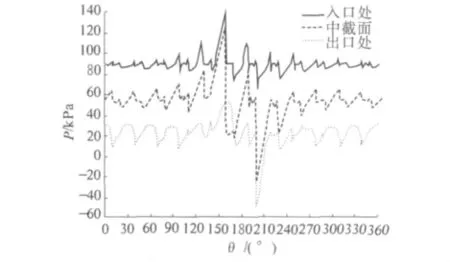
图3 不同截面水膜压力分布(ε=0.6，n=1 000 r/min)Fig.3 Water film pressure distribution of different sections(ε =0.6，n=1 000 r/min)

3.1.3 偏心率对水膜压力分布的影响

图4给出了转速为800 r/min，偏心率ε分别为0.7和0.8时中截面水膜压力分布曲线.不同偏心率下，中截面最大水膜压力出现在不同板条位置.由曲线可知，随着偏心率增大，最大水膜压力出现位置越远离轴颈下方板条，并且偏心率对水膜压力的影响较小.

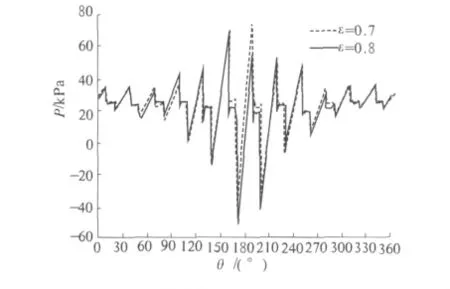
图4 不同偏心率下水膜压力分布Fig.4 Water film pressure distribution in different eccentricity

3.2 橡胶弹性变形和水膜厚度分布

3.2.1 转速对橡胶弹性变形分布的影响

图5 不同转速下橡胶弹性变形分布Fig.5 Elastic deformation distribution of rubber in different rotate speed

由于水润滑橡胶合金轴承材料弹性模量较低，易发生变形，对水膜厚度的影响较大.图5给出了偏心率为0.6，不同转速下的橡胶弹性变形分布云图.可以看出，随着转速的增大，流体动压效应越明显，橡胶的变形也越大.在轴承两端和凹槽附近，橡胶的变形较大，且最大变形量发生在入口处.

3.2.2 水膜厚度分布

水膜厚度由刚性间隙和橡胶的弹性变形组成.图6给出了偏心率为0.6，转速为1 000 r/min下轴承中截面水膜厚度分布曲线.凹槽处与板条处的水膜厚度相差较大，主要取决于凹槽的几何深度.凹槽处的水膜压力较小，故该处橡胶的变形也较小.不同板条，水膜厚度变化较大，主要是轴颈偏心引起的刚性间隙变化.同一板条水膜厚度除了受轴颈偏心影响以外，还受橡胶变形的影响.特别是轴颈下方即120°≤θ≤240°板条上，水膜厚度变化显著.

图6 中截面水膜厚度分布(ε=0.6，n=1 000 r/min)Fig.6 Waterfilm thickness distribution of middle section

图7 给出了偏心为0.6时，不同转速下水膜厚度分布曲线.当转速为100 r/min时，轴颈下方板条的水膜厚度基本为轴承刚性间隙.随着转速的增大，水膜厚度变化也越大.在板条入口处和出口处，膜厚先减小后增大，随后再减小.这是由于橡胶向凹槽方向变形，形成凸峰所致.随着转速的增大，橡胶变形越大，故这种板条颈缩现象越显著.

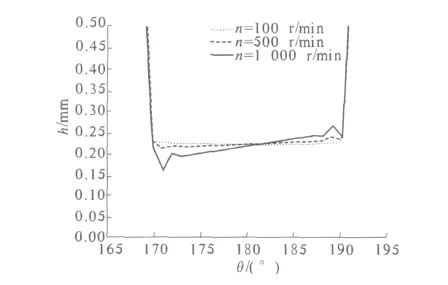
图7 不同转速下水膜厚度分布Fig.7 Waterfilm thickness distribution in different rotate speed

图8 给出了转速为800 r/min时，不同偏心率下水膜厚度分布曲线.可以看出，随着偏心率的增大，水膜厚度越小，但橡胶变形量占水膜厚度的比重越大.此时，板条颈缩现象同样存在.

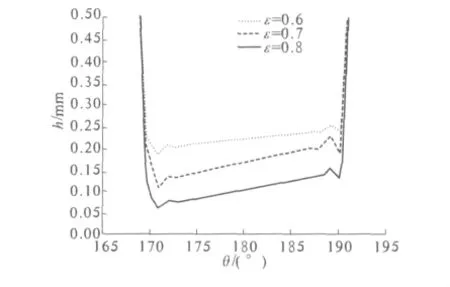
图8 不同偏心率下水膜厚度分布Fig.8 Waterfilm thickness distribution in different eccentricity

3.3 承载能力和摩擦系数

图9 给出了偏心率为0.65时，转速对承载能力的影响.随着转速的增大，流体动压效应越显著，承载能力越大.当转速n＜700 r/min时，承载能力随转速成线性比例增大;当转速n＞700 r/min时，承载能力随转速成指数增大.

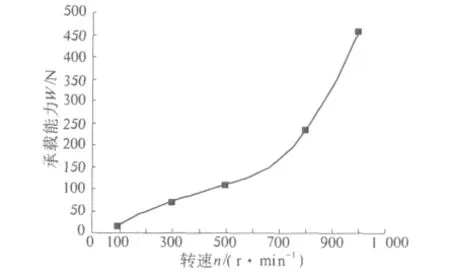
图9 转速对承载能力的影响Fig.9 Effect of rotate speed on carrying capacity

图10 给出了转速为300和800 r/min时，偏心率对承载能力的影响，结果表明:转速较高时，增大偏心率，能大幅度提高轴承的承载能力.

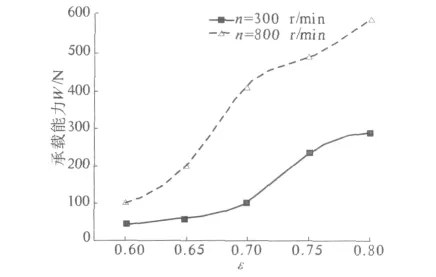
图10 偏心率对承载能力的影响Fig.10 Effect of eccentricity on carrying capacity

图11给出了转速和偏心率对摩擦系数的影响.结果表明:摩擦系数趋于平稳，随偏心率和转速的变化影响较小.这是由于黏性摩擦力和承载力均随转速的增大而增大，故比值趋于平稳.当转速较高时，承载力增大的较多，故摩擦系数在高转速时略有降低.

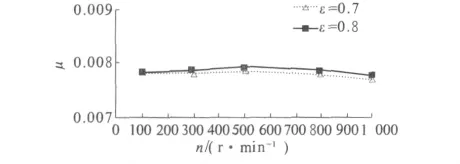
图11 转速和偏心率对摩擦系数的影响Fig.11 Effect of rotate speed and eccentricity on carrying capacity

4 结论

(1)考虑实际工况条件以及多曲面、多纵向凹槽的几何结构，分析了转速和偏心率对水膜压力分布影响，结果表明:转速越大，流体动压效应越显著，水膜压力越大;偏心率越大，最大水膜压力出现的位置越远离轴颈下方板条.

(2)水膜厚度由刚性间隙和橡胶弹性变形组成，特别是轴颈下方即120°≤θ≤240°板条上，水膜厚度变化显著.随着转速增大，橡胶变形增大，出现颈缩的现象越显著.

(3)低速时，承载能力随转速成线性比例增大;高速时，承载能力随转速成指数增大.

(4)不考虑轴承的接触和表面粗糙度，仅考虑水润滑橡胶合金轴承处于全水膜弹流润滑状态下，转速和偏心率对摩擦系数影响较小.

［1］ PAI R，HARGREAVES D J，BROWN R.Modelling of fluid flow in A3-axial groove water bearing using computational fluid dynamics［C］//14th Australasian Fluid Mechanics Conference.Adelaide， Australia，2001:10-14.

［2］ MAJUMDAR B C，PAI R，HARGREAVESD J.Analysis of water-lubricated journal bearings with multiple axial Grooves［J］.Journal of Engineering Tribology，2004，218:135-146.

［3］ TAN K H，RYAN T.Modelling of fluid flow in multiple axial groove water lubricated bearings using computational fluid dynamics［D］.Brisbane:Queensland U-niversity of Technology，2007.

［4］ PAI R S，PAI R.Stability of four-axial and six-axial groove water lubricated journal bearings under dynamic load［J］.Proc Instn Mech Engrs，Part J:J Engineering Tribology，2008，222:683-691.

［5］ ALEX DE K，VAN OSTAYEN R A J，RIXEN D J.Calculation of Stribeck curves for(water)lubricated journal bearings［J］.Tribology International，2007，40:459-469.

［6］ CABRERA D L，WOOLLEY N H，ALLANSON D R.Film pressure distribution in water-lubricated rubber journal bearings［J］.IMechE，2005，219:125-132.

［7］ 卢磊，王家序，肖科.基于ANSYS多物理场的水润滑轴承的数值分析［J］.机械设计，2010，10(10):93-96.

［8］ WANGJX，HANY F，ZHOUGW，et al.Numerical analysis of concave-slab type water lubricated rubber alloy bearings’lubrication ［J］.Applied Mechanics and Materials，2011，86:805-808.