一类含输入和状态时滞的不确定非线性系统的鲁棒控制
2012-12-03朱作键
王 坤,朱作键
(燕山大学理学院,河北秦皇岛066004)
0 引言
时滞性、非线性以及参数不确定性在实际控制系统中是普遍存在的.例如,许多网络化控制系统是同时含状态时滞和输入时滞的非线性系统,而且通常两种时滞是不同的.时滞往往是系统产生振荡、不稳定和性能变差的根源,这就增加了系统分析和研究的难度,因而,时滞系统的研究一直受到众多学者的关注,特别是非线性时滞系统的研究.在对非线性时滞系统的研究中,文献[1-3]的作者研究了具有状态时滞的非线性系统的鲁棒控制.文献[4]的作者分析研究了含有多输入时滞非线性系统的鲁棒控制.文献[5-12]的作者针对含状态时滞和输入时滞的不确定非线性时滞系统,研究了系统的鲁棒稳定性及反馈控制律设计问题.这些文献并没有针对同时具有状态时滞、输入时滞和非线性扰动(含有双时滞)的不确定时滞系统进行详细讨论.笔者在此基础上,针对一类同时具有输入时滞、状态时滞和非线性扰动(含有双时滞)的不确定系统,讨论了此类系统的鲁棒控制问题.首先,通过选择适当积分形式的Lyapunov函数;然后,结合矩阵分析理论和鲁棒稳定理论,利用线性矩阵不等式(LMI)性质,推导出此系统鲁棒渐近稳定的一个充分条件,并给出了一个相应的状态反馈控制律;最后,通过数值算例验证了此结论的可行性以及有效性.
1 问题描述
考虑如下不确定非线性时滞系统:
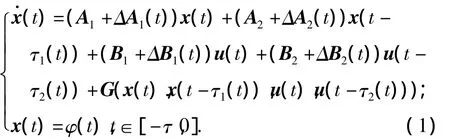
式中:x(t)∈Rn是系统的状态向量;u(t)∈Rm是控制输入向量;τ1(t)、τ2(t)分别是系统状态滞后和输入滞后,且对所有的t,满足


式中:H、E1、E2、E3和E4是已知的具有适当维数的实常数矩阵;F(t)是具有Lebesgue可测元的未知实矩阵函数,且满足FT(t)F(t)≤I,其中,I为适当维数的单位矩阵.

是时变的非线性扰动.系统受外界的影响是经常变化的,可能偏离正常或预期的情况,这种外界影响的变化称为扰动,其一般都在一定范围内变化,即满足∀t∈[0,+∞),

其中,Hi(i=1,2,3,4)为已知的具有适当维数的实常数矩阵.
φ(t)∈Cn[- τ,0]是连续向量函数,表示系统的初始条件.
对于系统(1),研究其鲁棒稳定性,若[A1B1]能控,设计一个无记忆的状态反馈控制律u(t)=Kx(t)使得对所有允许的不确定性,导出的闭环系统:

是鲁棒渐近稳定的.

则式(5)可写成:

为研究此系统的鲁棒控制问题,引入两个引理,如下:
引理1[13]记X,Y,Z为适当维数的实矩阵且ZTZ≤I,对于任意的标量 ε>0,下列不等式成立
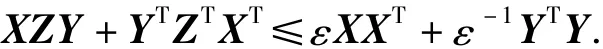
引理2[13]若给定对称正定矩阵X,Y和对称负定矩阵Z,有

则存在标量λ>0,使得

2 主要结果
2.1 主要结果思路分析
针对系统(5),在矩阵分析理论和鲁棒稳定理论基础上,对其进行了分析研究,得到了两个关于系统鲁棒稳定的主要定理,并对定理进行了相应的证明.
第一个定理证明主要思路及步骤:①选择适当积分形式的Lyapunov函数,并进行求导;②结合引理1和条件(4),利用线性矩阵不等式(LMI)性质推导出此类时滞系统的一个与不确定性相关的鲁棒渐近稳定的充分条件,并给出了一个保证此类系统鲁棒渐近稳定的状态反馈控制律.
第二个定理证明主要思路及步骤:在定理1的基础上,利用引理1,2对定理1进一步推导,结合Schur引理,得到一个确定的鲁棒渐近稳定的充分条件和状态反馈控制律.
2.2 主要结果及证明
定理2.1 如果存在矩阵K∈Rm×n,和对称正定矩阵 P1,P2,P3∈Rn×n使得对任意允许的不确定性F(t),系统(5)满足:

则系统(5)是鲁棒渐进稳定的,且u(t)=Kx(t)是系统(1)的一个状态反馈控制律.其中,

证明 取Lyapunov函数

其中,
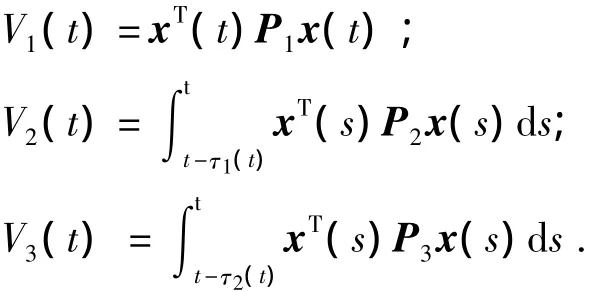
沿系统(5)的任意轨迹,对V(t)求导:
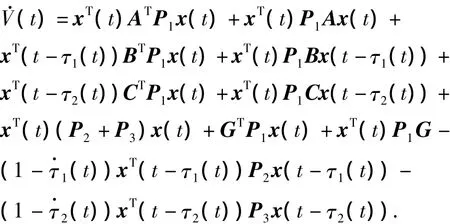
由式(4)和引理1知,

于是,再由式(2)知:
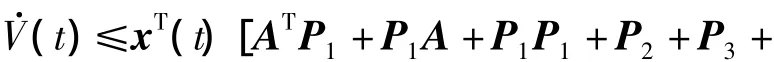

由鲁棒渐近稳定的定义知,系统(5)鲁棒渐近稳定的充分条件是式(6)成立,且u(t)=K·x(t)是系统(1)的一个状态反馈控制律.其中,P=P1A+ATP1+P1P1+P2+P3+H1TH1+K T H3TH3K证毕.
定理2.2 如果存在矩阵 Y∈Rm×n,对称正定矩阵 X,Q1,Q2∈Rn×n和标量 ε >0 使得系统(5)满足下式(7):

则系统(5)是鲁棒渐进稳定的,且u(t)=YX-1x(t)是系统(1)的一个状态控制律.其中,

证明 基于定理1,显然,式(6)可写成

其中,标称项为
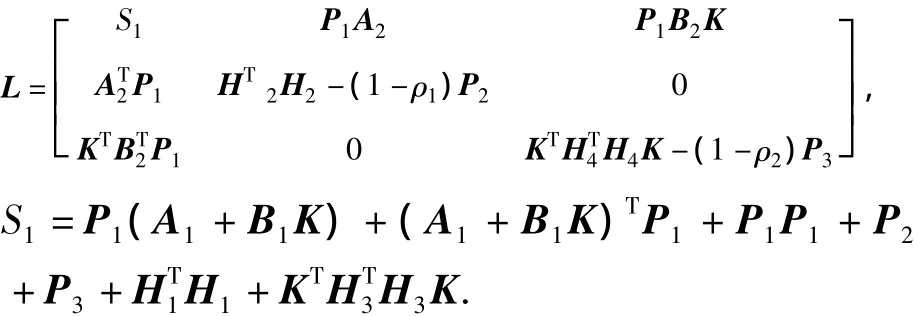
不确定项为

不等式(8)等价于对任意具有适当维数的非零向量α,有
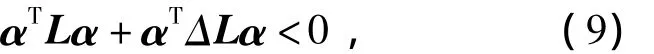
显然

而且上式在
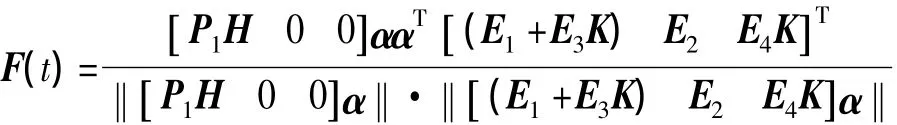
时取最大值,对于此F(t)值,不等式(9)必须满足,即

其中,

显然式(10)成立,必须有L<0,且

由引理2知,存在标量ε>0使得
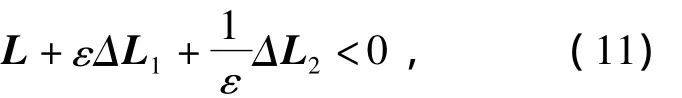
再由引理1知,对于标量ε>0使得
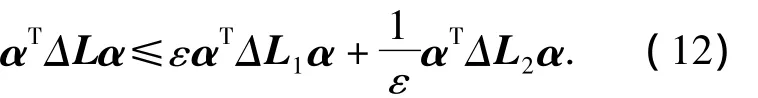
由式(11)、(12)以及Schur引理推导知,不等式(9)等价于式(13).
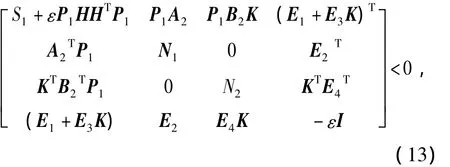
记 X=P-11,Y=KX,Q1=XP2X,Q2=XP3X.对式(13)同时左乘和右乘 diag{X,X,X,I},结合Schur引理,经过整理,得到式(7),即式(13)等价于式(7).
易知K=YX-1,u(t)=YX-1x(t)是系统(1)的一个状态反馈控制律.证毕.
2.3 结果比较
非线性扰动是大多数时滞系统都存在的一个问题.本结果是在考虑输入时滞与状态时滞的基础上,进一步考虑了非线性扰动对系统稳定性的影响所得出的结论.与只考虑输入时滞和状态时滞的系统所得出的结论比较,与实际更接近,适用范围更广.
文献[10]针对一类同时具有状态和输入时滞的不确定广义系统,研究其鲁棒预测控制问题,得到了一个分段的稳定性条件和分段连续状态反馈控制律Kk,同时没有考虑非线性扰动对系统稳定性的影响,具有一定的保守性,而此结果考虑了此因素,并得到了一个无记忆的连续状态反馈控制律u(t)=YX-1x(t),相对降低了系统的保守性.由此可见,此时滞系统具有一定的研究意义.
3 数值仿真
考虑具有如下参数的不确定非线性时滞系统(1):


且满足式(5).取 τ=0.4,ρ1=0.2,ρ2=0.4,由 MATLAB中LMI工具箱[14]解线性矩阵不等式(7),求得增益矩阵 K= [-11.775 3 -0.609 6],即系统(1)的一个状态反馈控制律为:
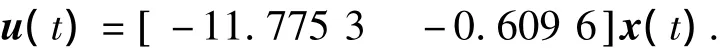
不失一般性,图1(a)为取 τ1(t)=0.2,τ2(t)=0.4时闭环系统的状态响应图.图1(b)为取τ1(t)=0.1,τ2(t)=0.2 时闭环系统的状态响应图,可见结论是可行且有效的.

图1 闭环系统状态响应图Fig.1 State response figure of closed-loop system
4 结论
笔者讨论了一类具有输入时滞和状态时滞的不确定非线性系统的鲁棒渐近稳定性及状态反馈控制律的设计问题.在适当条件下,通过选择适当的Lyapunov函数,结合矩阵分析理论和鲁棒控制理论,利用线性矩阵不等式(LMI)性质,得到了依赖时滞的系统鲁棒渐近稳定的一个充分条件,并给出了该系统一个相应的状态反馈控制律u(t)=YX-1x(t).最后,通过数值模拟验证了此结论的可行性以及有效性.
[1] ZHANGYin-ping,SUN Ji-tao.Robust synchronization of coupled delayed neural networks undergeneral impulsive control[J].Chaos,Solitons and Fractals,2009,41:1476-1480.
[2] 王玉芬,张高民,王中凤.含非线性扰动的不确定时滞系统的鲁棒控制[J].控制工程,2009,16(Z):90-93.
[3] 李杰,王汝凉,梅昆波,等.一类不确定非线性时变时滞系统的鲁棒控制[J].广西师范学院学报:自然科学版,2010,27(4):21-24.
[4] 王春晓,唐慧玉,李俊民.多输入非线性时滞系统的鲁棒稳定性设计[J].山东建筑工程学院学报,2005,20(2):65-69.
[5] CHO H J,PARK JH.Novel delay-dependent robust stability criterion of delayed cellular neural networks[J].Chaos,Solitons and Fractals,2007,32:1194-1200.
[6] LOU Xu-yang,CUI Bao-tong.On the global robust asymptotic stability of BAMneural networks with timevarying delays[J],Neurocomputing,2006,70:273-279.
[7] CHEN Bing,LIU Xiao-ping,LIN Chong,et al.H∞control of Takagi-Sugeno fuzzy systems with state and input time delays[J].Fuzzy Sets and Systems,2009 ,160:403-422.
[8] LI Li,LIU Xiao-dong.New approach on robust stability for uncertain T-Sfuzzy systems with state and input delays[J].Chaos,Solitons and Fractals,2009,40:2329-2339.
[9] LIEN Chang-hua,YU Ker-wei.Robust control for Takagi-Sugeno fuzzy systems with time-var-ying state and input delays[J].Chaos,Solitons and Fractals,2008,35:1003-1008.
[10]刘晓华,王利杰.带有状态和输入时滞的不确定广义系统的鲁棒预测控制[J].控制理论与应用,2010,27(4):527-532.
[11]李永钊,吴保卫.带状态时滞和输入时滞的不确定非线性系统的鲁棒H∞控制[J].河南师范大学学报:自然科学版,2010,38(2):1-7.
[12]范蓉蓉,张小美,陆国平.具有状态时滞和输入时滞的非线性系统的鲁棒无源控制[J].南通大学学报:自然科学版,2010,9(4):6-11.
[13]苏宏业,褚健,鲁仁全,等.不确定时滞系统的鲁棒控制理论[M].北京:科学出版社,2007:81.
[14]俞立.鲁棒控制—线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:241-260.
