反舰导弹末制导律三维仿真技术研究

张 刚， 王文双， 张东兴， 李相平

（1．海军航空工程学院 电子信息工程系，山东 烟台264001；2．海军航空工程学院 科研部，山东 烟台264001）

0 引言

2制导律是描述导弹在向目标接近过程中所遵循的运动规律，决定了导弹的弹道特性及相应的弹道参数［1］。导弹制导律对导弹的速度、过载、制导精度和单发杀伤概率有直接影响。制导律分为经典制导律和基于现代控制理论的现代制导律［2］。经典制导律有追踪法、平行接近法、比例导引及各种改进形式等，现代制导律有最优控制制导律，微分对策制导律、自适应制导律、微分几何制导律、反馈线性化制导律、神经网络制导律，H∞制导律等。目前反舰导弹采用的传感器日趋多样化，有雷达、红外、电视制导、激光制导等，对导弹的拦截能力也逐步提高。在反舰导弹的总体设计和打击效能评估中，在如此众多的制导体制和制导律中选择出最恰当的制导律是一个非常重要的问题。通过计算机建模仿真，可以根据设定的场景对不同的制导律进行性能对比。不同的制导律表达形式不同，且通常给出的是二维平面的表达形式，而反舰导弹攻击目标的过程是一个三维空间的运动。针对以上情形建立一个较为通用的模型，进行三维制导律的建模仿真是非常必要的。

目前三维制导律仿真建模方法主要有以下几种：

a）第一种采用差分方法建模［3］，给出比例导引的理想弹道轨迹，若改用其它制导律，模型修改复杂；

b）第二种是将三维弹道解耦到发射坐标系的铅垂面和水平面中，该分解方法对落角约束的制导律仿真不精确；

c）第三种是将末制导的三维运动分解为垂直平面和水平面的运动［4］，该分解方法适应性广，但是由于给出的垂直平面仅包含弹目视线，导弹速度矢量和目标速度矢量并不在该平面内，仿真存在近似；

d）第四种是在视线坐标系内将末制导过程的弹目相对运动解耦成纵向平面的运动和侧向平面的运动，该模型精确，但是需要多次坐标转换，且给出的制导律形式较为复杂［2，5］。

本文采用第三种解耦仿真模型，末制导的三维运动分解为垂直平面和水平面的运动，给出了详细的仿真流程，并采用比例导引、最优制导律、带落角约束的制导律进行仿真，验证了模型的有效性。

1 反舰导弹—目标相对运动模型

1．1 导弹和目标的相对运动方程

导弹和目标的相对运动关系如图1所示，OXYZ为参考坐标系，XOZ与水平面平行，其中M为导弹、T为目标，MT为弹目视线连线。qy为弹目视线与XOZ面的夹角即视线倾角，qz为弹目视线在XOZ的偏角，即视线偏角；导弹的速度为Vm，弹道倾角为θm，弹道偏角为ψm；目标的速度为Vt，弹道倾角为θt，弹道偏角为ψt，对于水平面上运动的目标，显然，θt＝0。俯仰方向的角度，以水平面为基准，逆时针旋转为正，取值范围为 ［－π／2，π／2］；偏航方向的角度，以 OX轴为基准，由OY轴俯视时，逆时针旋转为正，取值范围为 （－π，π］。

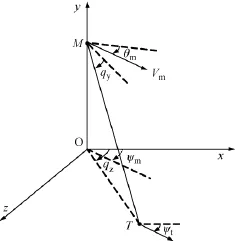
图1 反舰导弹末制导弹目空间模型

图1中，弹目三维运动可以解耦成垂直平面和水平面的运动，在两个平面上分别运用制导律，即可合成导弹—目标在三维空间内的运动轨迹。导弹速度和目标速度在OXYZ坐标系上的分量为

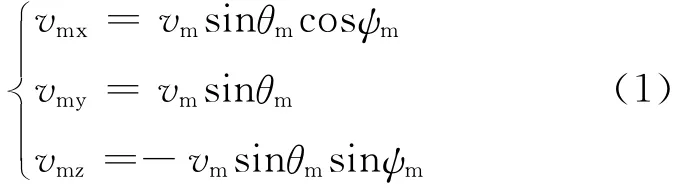
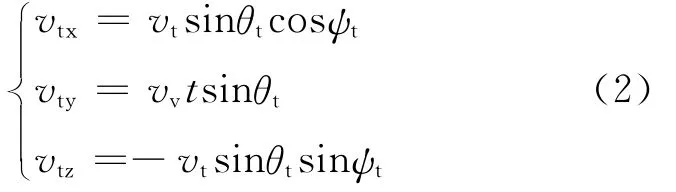
1．2 垂直平面相对运动方程

垂直平面内导弹—目标的相对运动模型如图2所示。

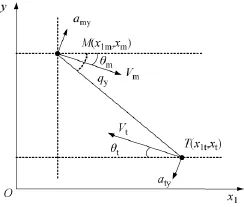
图2 纵平面导弹—目标的相对运动模型

该平面为包含弹目视线的垂直平面。图2中，M表示导弹，坐标为（x1m，ym）；T表示目标，坐标为（x1t，yt）；amy为导弹纵向加速度，aty为目标纵向加速度，对于水面舰艇目标，aty＝0，目标弹道倾角θt＝0。导弹—目标的相对运动方程为

1．3 水平面相对运动方程

水平面内导弹—目标的相对运动模型如图3所示。

方：您虽非图书情报专业出身，但是从80年代中期开始您在图书馆学方面的研究成果频频被专业核心期刊收录，其中除了辛勤付出之外，还有何成功秘笈？

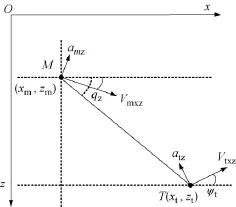
图3 水平面导弹—目标的相对运动模型

图3中，M 表示导弹，坐标为 （xm，zm）；T 表示目标，坐标为 （xt，zt）；amz为导弹水平面加速度，atz为目标水平面加速度，Vmxz、Vtxz是水平面上的导弹、目标速度，rxz是水平面上的弹目距离。导弹—目标的相对运动方程为

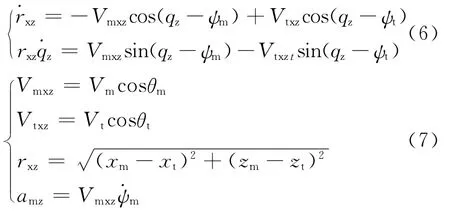
弹目视线角为

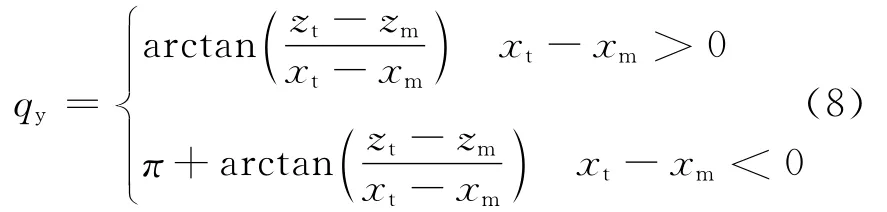
2 三维制导律仿真模型

2．1 仿真流程

三维末制导律的仿真流程如图4所示。仿真过程中，要在程序开始时初始化导弹、目标的速度、坐标、弹道倾角、弹道偏角等参数。初始化完成后开始循环，循环中首先计算弹目相对距离、qy、qz及垂直平面和水平面的参数；其次根据弹目相对运动方 程，分 别 求 出˙r，˙rxz、˙qy，˙qz；再 次 根 据选择的制导律分别计算amy，amz，对导弹目标坐标、导弹倾角、弹道偏角、弹目相对距离等变量进行更新，即得到新时刻的仿真变量值；最后根据设置的仿真结束条件，判断循环是否完成。如果循环完成，则画出弹目运动轨迹、导弹加速度amy，amz的变化曲线等图形。

仿真结束的条件可以设置为弹目相对距离小于某一数值，也可以判断弹目相对距离˙R，当˙R＞0，即认为导弹远离目标，仿真结束，用此种判定准则需要注意的是某些制导律可能会使导弹在末制导初段远离目标。本文针对舰船运动的特性，采用ym＜yt作为仿真结束准则。

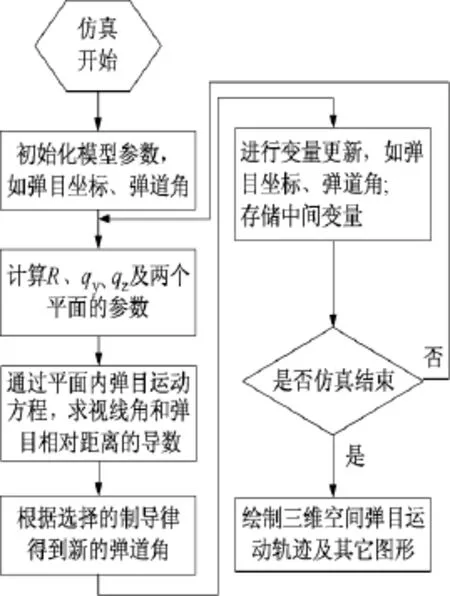
图4 三维制导律仿真流程图

在仿真过程中，为了提高模拟的精度，仿真步长要取得足够小。当相对距离R＞1 000 m时，取仿真步长dt＝0．01 s；当1 000 m＞R＞50 m，取仿真步长dt＝0．005 s；当R＜50 m，取仿真步长dt＝0．001 s，这样可以既精确计算出终端脱靶量，又避免计算负担过程，提高了仿真效率。

在实际的反舰导弹末制导中，导弹在距离目标很近时，雷达存在盲区，因此可以设置R＝200 m作为导弹的零控距离。导弹机动时，受到最大可用过载的限制，这些相关考虑也可以在仿真中根据需要合理设置。

2．2 采用的制导律

为了验证模型的正确型，本文采用比例导引和一种最优制导律和含有落角约束的制导律进行仿真。

比例导引制导律是当前导弹武器系统中广泛采用的制导律，它通过使速度矢量的转动角速度正比于目标视线的转动角速度，进而能够抑制视线转率。在垂直平面和水平面采用的比例导引形式为［6］

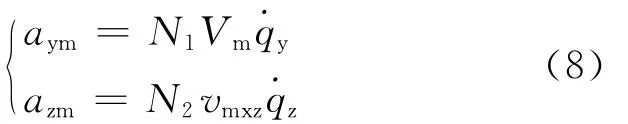
式中：比例导引的导航比N1＝N2＝3。

（2）最优制导律

该最优制导律是通过脱靶量指标和能量消耗均为最小指标，结合弹目运动方程推导出的制导律形式。文献［7］给出的制导律在垂直平面和水平面的表达式为

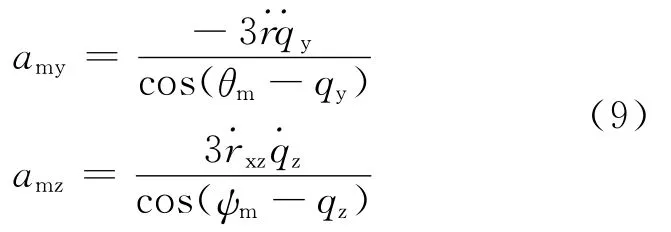
（3）带有落角约束的制导律

当对海面舰艇打击时，除了满足脱靶量和制导过程中能量消耗最小外，有时还要考虑弹着角的要求。下面是文献［4］给出的含有落角约束的制导律：

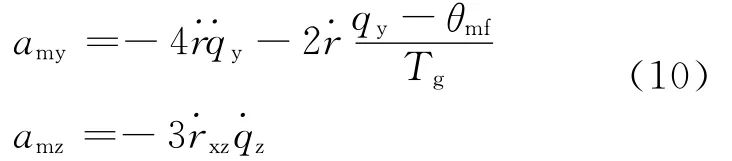
式中：Tg为剩余飞行时间，Tg＝－r／˙r；θmf是导弹击中目标时的速度倾角。

3 仿真结果分析

仿真1：通过比例导引和最优制导律验证模型。假设导弹初始坐标为（0，3 000，0），单位为米；导弹速度vm＝300 m／s，在惯性坐标系的弹道倾角θm＝0°，弹道偏角ψm＝0°；目标初始坐标为（8 000，0，1 000），单位为米；目标速度vt＝100 m／s，目标在水平面内做匀速直线运动，θt＝0°，ψt＝－20°，当弹目距离小于200 m时，垂直平面和水平面的制导指令为0，两种制导律下的三维弹道曲线如图5所示。

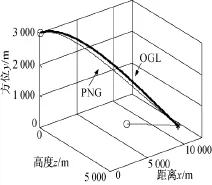
图5 三维弹道曲线

由图5可知，两种制导律均能击中目标，脱靶量均小于1 m，其中比例导引（PNG）弹目交会时间为43．44 s；最优制导律（OGL）弹目交会时间为43．73 s。如果降低目标速度，打击精度会进一步提高。

图6、图7分别为垂直平面、水平面上加速度随时间变化的曲线。从图中可以看出，最优制导律相对于比例导引，加速度变化要平缓些，这在实际中降低了对导弹过载的要求。两个制导律的加速度最终变为0，这是因为设置了停控距离。

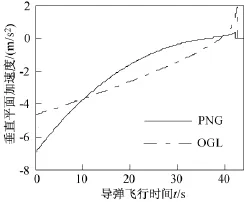
图6 时间与垂直平面加速度关系图

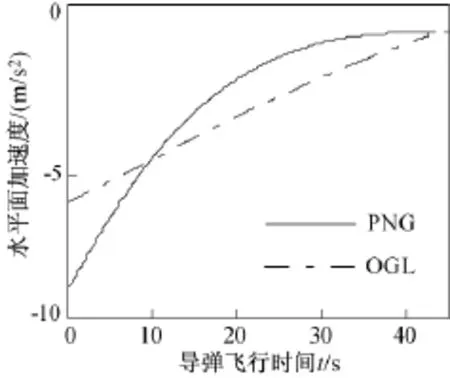
图7 时间与水平平面加速度关系图

仿真2：通过含落角约束的制导律验证模型。假设导弹初始坐标为（0，3 000，0），单位为米；导弹速度vm＝300 m／s，在惯性坐标系的弹道倾角θm＝0°，弹道偏角ψm＝0°，要求导弹击中目标时的速度倾角θmf＝80°；目标初始坐标为（8 000，0，1 000），单位为米；目标速度vt＝0 m／s，没有设置停控距离，对加速度也没有限制。弹目三维运动轨迹如图8所示。弹道以一定的弹道倾角击中目标，脱靶量小于1 m，弹目交会时间为32．12 s。

图9为垂直平面、水平面上加速度随之间变化的曲线。从图中可以看出，含有落角约束的制导律的加速度变化范围远远超过比例导引，这是由于落角约束引起的。图10为导弹倾角随时间的变化曲线，从图中可以看出，导弹的初始弹道倾角为0°，末端弹道倾角为80°，符合设计要求。

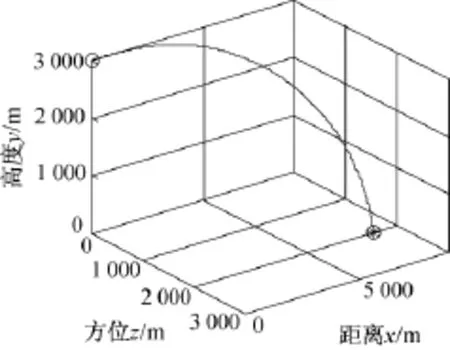
图8 带落角约束的制导律下的三维弹道曲线

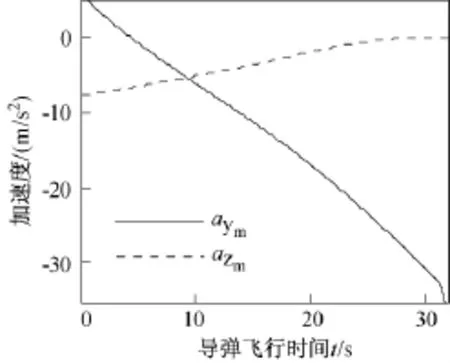
图9 时间与加速度关系图

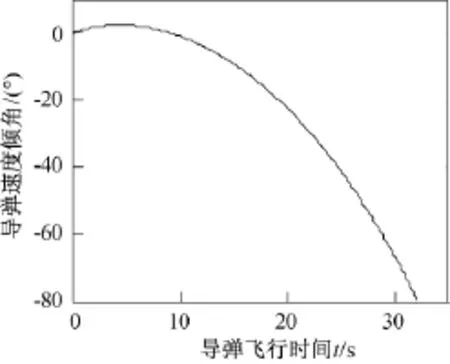
图10 时间与导弹速度倾角关系图

4 结束语

三维末制导律的研究与仿真是反舰导弹总体设计、效能评估的的必备步骤，由于制导律种类多、符号体系、坐标体系多种多样，给制导律系能研究和不同制导律的比较带来很大的困难。本文采用二维解耦合的方法，将三维制导分解为垂直平面、水平面的制导，分别在这两个正交平面上实现不同的制导律，经过运动轨迹的合成，能够实现三维末制导律的仿真。该分解具有层次清晰、结构简单的特点。对于反舰导弹打击海面舰艇的场景，分别采用比例导引制导律、一种最优制导律和一种含有落角约束的制导律，实现对该模型的验证，给出了仿真模型的实现细节。仿真结果表明，该模型具有简单、通用性的特点。通过修改模型中垂直平面加速度amy，水平面加速度amz的表达式，即可实现不同制导律的仿真，这有利于在实际工作中快速比较不同制导律的性能。

［1］ 钱杏芳，林瑞雄，赵亚男．导弹飞行力学［M］．北京：北京理工大学出版社，2006．

［2］ 张友安，胡云安［M］．北京：国防工业出版社，2003．

［3］ 高尚．比例导引理想弹道仿真［J］．计算机工程与设计，2003，24（8）：66－68．

［4］ 王颖，宋龙，张拥军．制导滑翔炸弹的最优末制导律研究［J］．弹箭与制导学报，2010，30（4）：51－54．

［5］ 黄玲玲．巡航导弹的三维精确末制导律及三维动画仿真研究［D］．南京：南京航空航天大学，2007．

［6］ 王亚飞，方洋旺，周晓滨．比例导引律研究现状及其发展［J］．火力与指挥控制，2007，32（10）：8－12．

［7］ 赵红超，王凤莲，顾文锦．超音速反舰导弹的最优末制导律研究［J］．航空兵器，2005，（3）：8－11．