一种运动单站多普勒无源定位法

郁 涛

（中国电子科技集团公司第五十一所，上海201802）

0 引言

现有的基于多普勒频差的运动单站无源定位技术需要求解非线性方程［1－3］。而目前正在被研究的基于多普勒变化率的无源定位方法，通常需要和其它方法综合使用，才能实现定位任务，且多普勒变化率的工程测量相对比较困难［3－5］。

本文初步分析表明，基于多普勒变化率原理，利用匀速运动时的速度关系，运动单站可以仅基于多普勒测量而确定固定目标的位置。所给出的方法的主要特点在于应用角度变化率的概念从多普勒方程中导出了基于频差测量的多普勒变化率计算公式，从而以极其简单的方式解决了多普勒变化率的工程测量问题。

1 基于频差测量的机载多普勒变化率

如图1所示，假定目标静止或低速运动，运动探测平台从节点位置1匀速直线运动到节点2，在节点1处由运动平台所接收到的多普勒频移方程为

式中：λ为波长；fd为多普勒频移；v为载机的飞行速度；β为前置角。

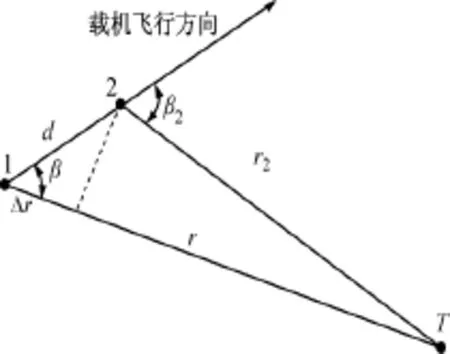
图1 分析运动单站多普勒变化率的几何模型

根据图1所示的几何关系，近似有如下的三角函数关系：

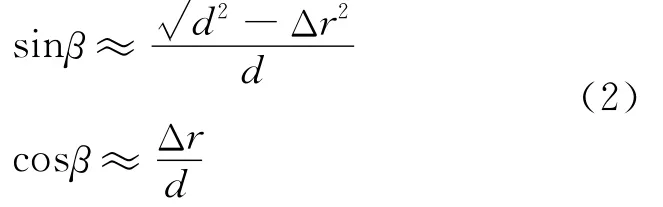
式中：d为在两个节点之间运动平台的飞行距离；Δr＝r1－r2是两节点间径向距离的路程差。

基于角度变化率的概念［6］，将有

在多普勒频移方程的右边实施微分变换，在利用了上述的三角函数关系式后可得

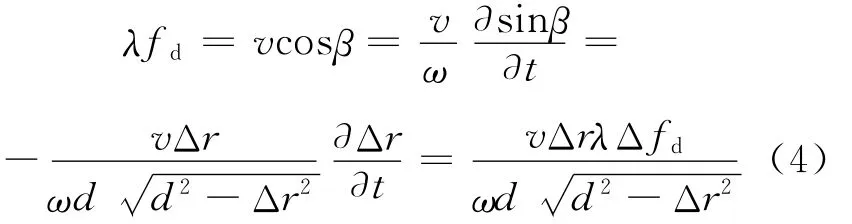
式中：ω＝∂β／∂t为角速度；Δfd＝fd2－fd1是两探测节点间的多普勒频差。

继续利用三角函数关系，经整理后有

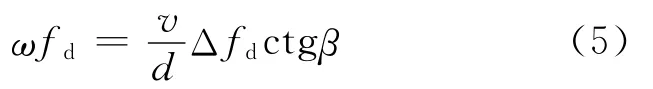
进一步利用角速度表示式：ω＝vt／r和多普勒频移方程对方程式（5）做变形整理得

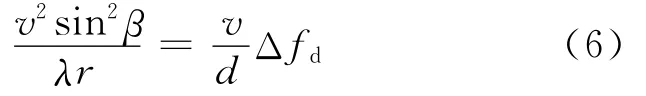
在运动平台匀速运动时，方程的左边即为多普勒变化率的基本表示式：

于是就得到了仅基于频差测量的多普勒变化率的计算式：

由此说明，引起多普勒变化的时间变化量可用运动平台的飞行距离与自身移动速度的比值来等效表示。

又因为有

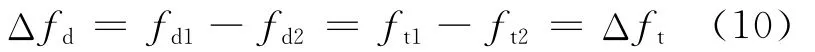
式中：fti为信号频率的实测值。即对多普勒变化率计算能由实测频差值所确定。

2 多普勒定位公式

2．1 相邻节点间多普勒变化率之比

设匀速直线移动的平台定周期探测目标信号，且至少连续探测三次，其几何关系如图2所示。在各个探测节点位置处的多普勒频移变化率的表达式为式中：vt为切向速度。

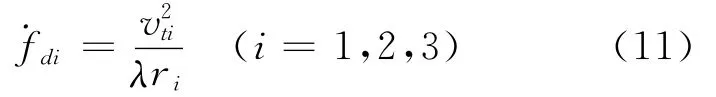
相邻节点间多普勒变化率的比值为

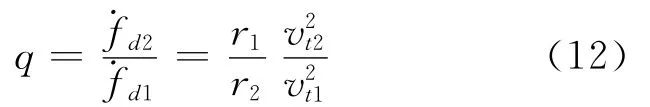
又由正弦定理可得到相邻节点位置处的径向距离之比为

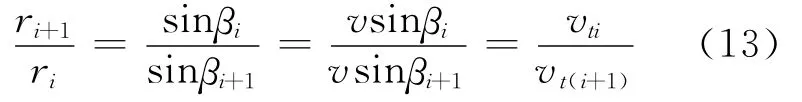
即在运动平台匀速运动的情况下，相邻节点间的径向距离之比等于切向速度之比，将其代回式（12），得

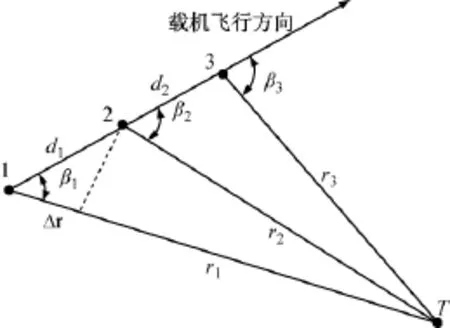
图2 分析运动单站多普勒无源定位的几何模型

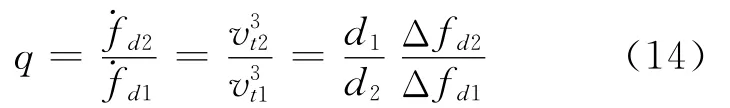
因此，在匀速运动的情况下，相邻节点的多普勒变化率之比将等于相邻切向速度之比的三次方。引用前一节推导得到的基于频差测量的多普勒变化率计算公式，可得到相邻节点多普勒变化率的比值为

2．2 径向距离

根据平台飞行路径上各个节点位置处的速度分量，可列出如下的速度恒等式：

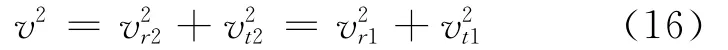
式中：vr为径向速度。

变形整理后，有

分别将多普勒频移方程和多普勒变化率及比值代入：

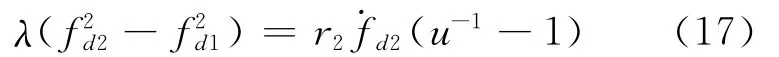
其中：

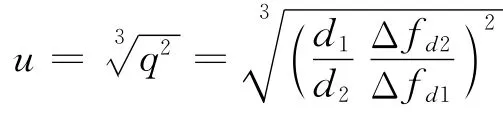
由此，即可得到径向距离的计算值：

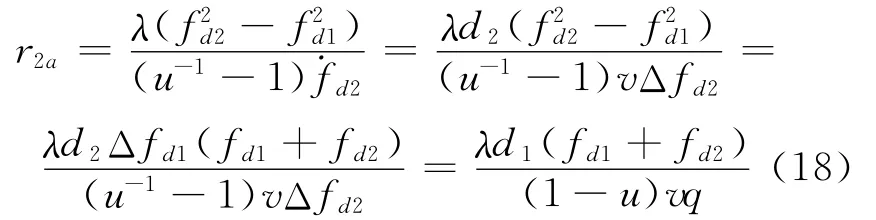
根据在理论值与计算值之间的误差公式：

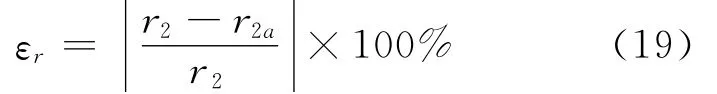
图3和图4分别给出了在等距与不等距移动时的测距误差，从中可看出，在相邻两飞行距离相等时，计算公式具有最好的计算准确性，不等距将会引起较大的计算误差，在前置角趋于90°时存有发散现象。模拟验证表明，计算误差与移动平台的飞行速度和被测信号的波长无关。

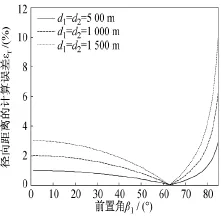
图3 等距探测时测距公式的计算误差

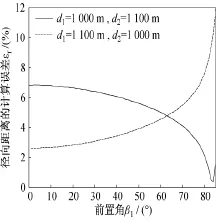
图4 不等距探测时测距公式的计算误差

计算所选用的基本参数：

载机飞行速度：v＝100 m／s

初始径向距离：r1＝100 km

目标信号波长：λ＝0．25 m

2．3 测向公式

在目标的径向距离被确定的情况下，再次利用多普勒变化率的基本表达式（7），则即能获得前置角，即目标相对方位的计算公式：

图5给出了不同基线长度时相对方位的计算误差。计算表明，减小移动距离有利于降低计算误差。当前置角趋于90°时将出现发散。

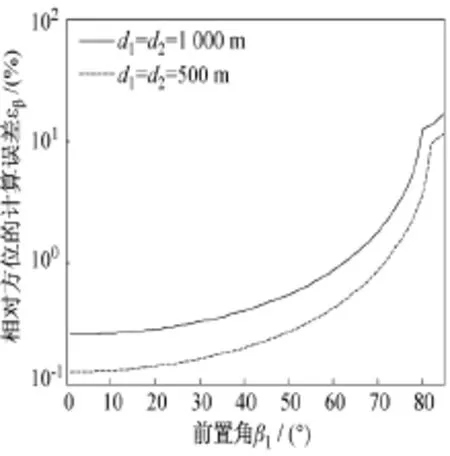
图5 相对方位的计算误差

3 结束语

和先前的若干研究结果相比［7，8］，本文更为完整的描述了仅基于多普勒测量实现运动单站无源实时定位的方法。

事实上，相差干涉测向法也是一种与频率相关的测量方法，相比之下，运动单站多普勒定位法的优点在于：不需要求解整周数，又能够直接对目标距离实现测量。但由于是多点探测，故运动单站多普勒无源定位可能并不十分适用于对频变信号的探测。

［1］ 张正明，杨绍全．多普勒频率差定位技术研究［J］．西安电子科技大学学报，1999，27（6）：786－789．

［2］ 张波，石昭祥．差分多普勒定位技术的仿真研究［J］．电光与控制，2009，16（3）：13－16．

［3］ 王本才，张国毅，侯慧群．无源定位技术研究［J］．舰船电子对抗，2006，29（6）：20－26．

［4］ 李宗华，肖予钦，周一宇，等．利用频域和空域信息的单站无源定位跟踪算法［J］．系统工程与电子技术，2004，26（5）：613－616．

［5］ 周振，王更辰．机载单站对机动目标无源定位与跟踪［J］．电光与控制，2008，15（3）：60－63．

［6］ 赵业福，李进华．无线电跟踪测量系统［M］．北京：国防工业出版社，2001．

［7］ 郁涛．基于多普勒频率的机载测距原理［J］．信息与电子工程，2011，9（1）：22－26．

［8］ 郁涛．基于角度变化率的机载多普勒直接测距方法［J］．航空工程进展，2011，2（3）：62－65．